Improved Shuffled Frog Leaping Algorithm Optimizing Integral Separated PID Control for Unmanned Hypersonic Vehicle

Liang Bingbing（梁冰冰），Jiang Ju（江驹），Zhen Ziyang（甄子洋）*，Ma Kun（马坤）

College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

Improved Shuffled Frog Leaping Algorithm Optimizing Integral Separated PID Control for Unmanned Hypersonic Vehicle

Liang Bingbing（梁冰冰），Jiang Ju（江驹），Zhen Ziyang（甄子洋）*，Ma Kun（马坤）

College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，P.R.China

To solve the flight control problem for unmanned hypersonic vehicles，a novel intelligent optimized control method is proposed.A flight control system based on integral separated proportional-integral-derivative（PID）control is designed for hypersonic vehicle，and an improved shuffled frog leaping algorithm is presented to optimize the control parameters.A nonlinear model of hypersonic vehicle is established to examine the dynamic characteristics achieved by the flight control system.Simulation results demonstrate that the proposed optimized controller can effectively achieve better flight control performance than the traditional controller.

hypersonic vehicles；flight control；shuffled frog leaping algorithm；unmanned aerial vehicles（UAVs）

0 Introduction

Hypersonic vehicles are designed to operate over a range of flight conditions from low subsonic speeds to flight at high Mach numbers in the uppermost part of the earth′s atmosphere.The research of air-breathing hypersonic vehicles poses unique challenges.Control techniques are one of the key technologies for these classes of aircrafts.Several control strategies have been proposed for the hypersonic flight vehicles.A robust tracking controller was designed，which achieved global exponential tracking control of a model reference system where the plant dynamics contained varying parametric uncertainties［1］.A controller was designed for rotation motion dynamics of a hypersonic vehicle，which contained inner-fast/ outer-fast loops nonlinear predictive controllers［2］.A tracking controller for an air-breathing hypersonic vehicle was proposed which used the aero-propulsive and the elevator-to-lift coupling to design controllers［3］.However，these methods are a little complex to be realized.Proportionalintegral-derivative（PID）control is still the most applicable engineering method for flight vehicles［4］.

Swarm intelligence（SI）is the collective intelligent behavior of decentralized，self-organized systems.Inspired from natural systems，several artificial SI algorithms are presented，including particle swarm optimization，ant colony optimization，artificial bee colony algorithm，differential evolution，artificial immune systems，which have been widely applied to robotics and other engineering fields.Shuffled frog leaping algorithm（SELA），originally proposed by Eusuff and Lansey［5-7］is another meta-heuristic SI algorithms inspired by biotic community.There are two analogies for this algorithm.One is the frogs swarm leaping on the stones to search for food by improving its memes.The other is a culture population such as an earlier culture which develops an idea such as pottery.Recently，SELA has been widely used in engineering，for instance，parameter identification［8］，control of selective and total harmonic distortion［9］，fuel management［10］，loss reduction and power generation of distributed generators［11］.Meanwhile，there have been several kinds of modifications for SELA.To further improve the local searching ability of SELA，a power law external optimization neighborhood searching strategy can be adopted［12］.Zhen，et al.presented a memetic algorithm［13］and an improvedSELA［14］.

Authors apply a controller design methodology here to an unmanned air-breathing hypersonic vehicle，which uses an integral separated PID controller to track velocity and pitch angle reference commands.Moreover，an improved SELA（ISELA）is presented to intelligently optimize the controller parameters which are difficult to be determined.

The modeling and control problem of unmanned hypersonic vehicle can be described by the following equations，defining a non-linear longitudinal model of the unmanned hypersonic vehicle

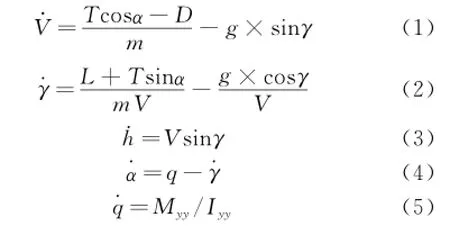
where m denotes the vehicle mass，V∈R the forward velocity，h∈R the altitude，α∈R the angle of attack，θ∈R the pitch angle，q∈R the pitch rate，T∈R the thrust，D∈R the drag，L∈R the lift，M∈R the pitching moment about the body y-axis，and Iyythe moment of inertia.

And

whereδeis the elevator deflection，and CTthe thrust coefficient

Dynamic model of the engine is expressed by a second-order differential equation

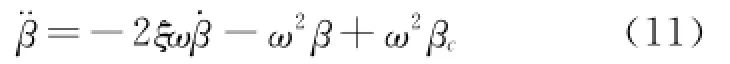
whereβis the engine throttle regulator variable，andβcthe throttle angle.

Elight control for unmanned hypersonic vehicles requires a high degree of precision，and even greater than that for a conventional aircraft in most cases.

1 Basic Shuffled Frog Leaping Algorithm and Its Improvement

In SELA，there is a population of frogs representing a set of possible solutions.The frog group is divided into several subsets referred to as memplexes，and each memeplex acts as an independent culture.Afterwards，the selection strategy of a submemplex in each memplex that the greater coefficients are considered for the frogs with better fitness functions is adopted.And then，local search starts from the worst frog to leap to the best frog in any memplex.After several generations of each memplex，ideas are passed between memeplexes in a shuffling process. The local search and the shuffling process continue until the solution criterion is satisfied.

1.1 Memeplexes partition

A population X=｛xi，fi，i=1，…，F｝of frogs is initialized with position within the searching domain and sorted in a descending order according to their fitness values where xidenotes the i-th frog′s position，and fiits fitness.The position of the frog with the best fitness is represented as xX.Partition the population into m memeplexes｛Y1，Y2，…，Ym｝.Each contains n frogs，and

1.2 Memeplexes evolution

Step 1 Since the frogs tend to concentrate around the best frog that may be a local optimum，some members in any memeplex are considered as a submemeplex（including q frogs）to avoid convergence to the local optimum.The weights are assigned with a triangular probability distribution.

The frogs with higher fitness have bigger weights and will be selected in the submemeplex.

Step 2 The worst frog in submemeplex leaps towards the best frog in the memplex，and the new position is thus obtained by a leaping step.

where xB，xWdenotes the best and the worstpositions of the submemeplex，respectively，Int（·）the rounding function，dmaxthe maximum step size allowed，r a random number，and k a generation number.If the new position of the worst frog is better than before，the position of the worst frog is updated by

Otherwise，the worst frog leaps towards the global best frog，then in Eq.（14）xBis replaced by xX.If the worst frog also cannot find a better solution，a random position is generated for the worst frog.

Step 3 Subsequently，the frogs are sorted in a descending order according to their fitness.Repeat Steps 1—3 and evolve the submemeplexes with G1generations.

1.3 Shuffle of memeplexes

After completed local search in each memeplex，all of memeplexs are shuffled，and the frogs are reorganized in a descending order of fitness.The population is repeatly divided into memeplexs，followed by the local search process，until memetic evolution generation G2is obtained.

1.4 Improvement of SFLA

The improved SELA（ISELA）is presented in three segments as follows:

（1）When the SELA is to solve continuous optimization problems，the leaping step needs to be modified into a continuous form.Hence the″Int″function should be canceled.Moreover，boundary limitation for the leaping step should also be canceled，and the substitute is the boundary limitation of frog position，in order to guarantee it in the feasible searching space.

（2）The partition strategy in the standard SELA is replaced by a random strategy，which is realized by the following method:generating a random number sequence，whose length is the size of the frogs swarm；sorting these random numbers，then the order sequence is obtained；selecting in turn a number of frogs in this order sequence to form a memeplex.

（3）The evolution of submemeplexes in SELA is the process of the worst frog to adjust its position，which is insufficient learning for the population，especially for the better frogs with fewer learning chances.Therefore，the submemeplexes is canceled and accordingly all the frogs in memeplexes can take part in the evolution.Eurthermore，the learning object in standard SELA is the best frog in submemeplex or in swarm.This singularity may cause the algorithm to fall into the local optimum.Therefore，in ISELA frogs can learn from any frog with a better performance.

According to the above modification，the leaping step of the i-th frog is modified as

The evolution of memeplexes is essenceially the process of mutual learning among the group. So the performance of the whole frog group is enhanced after the internal evolution and the gap between the best frog and the worst frog are decreased.

The implementation flow of the ISELA is shown in Eig.1.

2 Flight Control Laws for Unmanned Hypersonic Vehicle

The flight control system of unmanned hypersonic vehicle is composed of two control loops.One is the pitch angle loop，and the other the velocity loop.The control laws of these two loops are designed based on the integral separated PID control strategy，expressed by

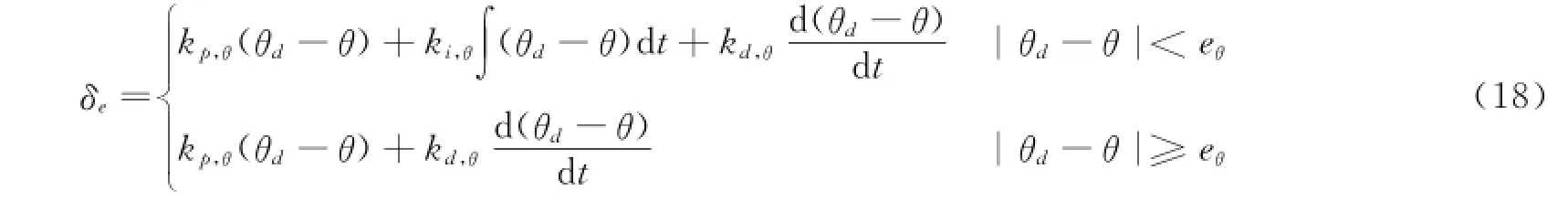
Eig.1 Elowchart of ISELA

It should be mentioned that the parameters vectorshould be determined in advance.Generally，the transfer functions are established and the root locus technique is adopted to design the control parameters. However，it is complex thus being hard to find optimal or near optimal parameters.

Therefore，ISELA is used to optimize the parameter vector K.The flowchart of ISELA describing the optimization process is shown in Eig.1.

3 Simulation and Analysis

To study the control performance of velocity and pitch attitude of an unmanned hypersonic vehicle in climbing flight，the vehicle is trimmed in level flight at 3 500 m/s and altitude of 30 500 m，as an initial flight state.The hypersonic vehicle is desired to track the velocity and pitch attitude references initialized at 3 200 m/s，5°，respectively.

Eor the proposed ISELA，the population size is set as 50，and the number of the memeplexes is 5 and 10 within each memeplex.Three memetic iterations in each memeplex and eight shuffling process in population are performed.The proposed ISELA optimized integral separated PID controller is compared with the traditional integral separated PID controller.Eor the sake of fairness，a set of parameters in the traditional integral separated PID controller is considered as initial candidate parameters in ISELA.

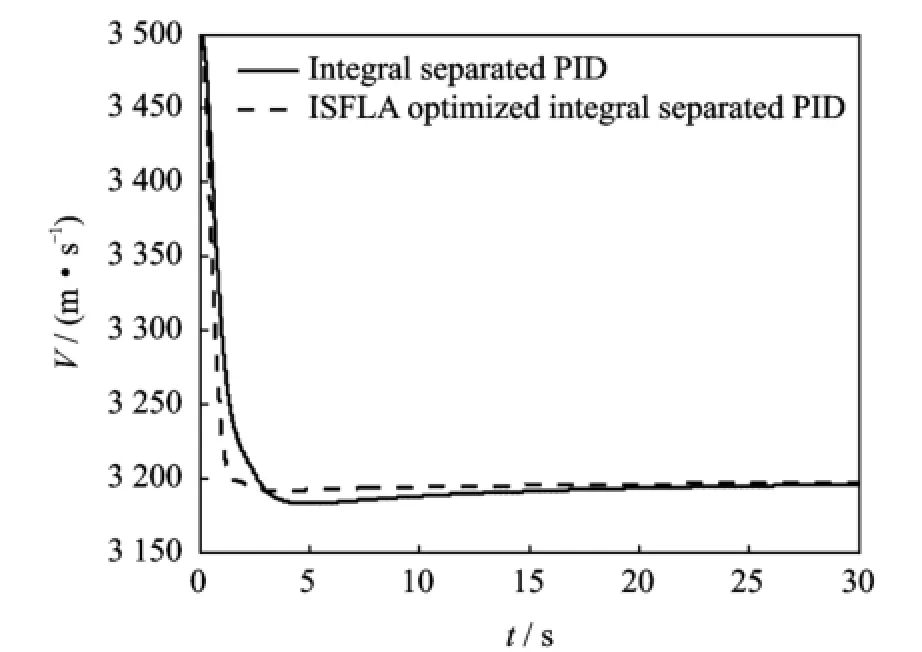
Eigs.2，3 show the velocity and pitch angle responses by the manipulation of elevator and throttle，under the integral separated PID controller and ISELA optimized integral separated PID controller，respectively.

Eig.2 Velocity response

Eig.3 Pitch attitude response

The above simulation results show that the proposed ISELA optimized integral separated PID controller is characterized by a faster dynamic re-sponse，a remarkably smaller error during the entire maneuver，and a higher steady error.Obviously，the improvement of control responses is benefit from the optimized controller parameters obtained by ISELA.

4 Conclusions

A nonlinear and physics-based model of the longitudinal dynamic model for an unmanned hypersonic vehicle is established.An integral separated PID control based flight control system of the hypersonic vehicle is designed for longitudinal maneuver control.The basic SELA is modified into a continuous form，therefore it can be used in the control parameter optimization problem，and the learning strategy is improved in terms of simplicity and fast convergence.And then，the ISELA is applied in control parameter optimization for obtaining a near optimal control gains.The simulation results demonstrate that the flight control system can achieve excellent pitch attitude angle and velocity tracking performance.Parameter optimization problem of the whole flight control system of the unmanned hypersonic vehicle is hoped to be solved in future work.

Acknowledgements

This work was supported in part by the National Natural Science Eoundation of China（No.61304223），the Specialized Research Eund for the Doctoral Program of Higher Education（No.20123218120015）and the Eundamental Research Eunds for the Central Universities（No. NZ2015206）.

［1］ Wilcox Z D，Mac Kunis W，Bhat S，et al.Robust nonlinear control of a hypersonic aircraft in the presence of aerothermoelastic effects［C］∥American Control Conference.Hyatt Regency Riverfront，St.Louis，MO，USA:［s.n.］，2009:2533-2538.

［2］ Wang Peng，Tang Guojian，Liu Luhua，et al.Nonlinear hierarchy-structured predictive control design for a generic hypersonic vehicle［J］.Science China: Technological Sciences，2013，56（8）:2025-2036.

［3］ Sun Hongfei，Yang Zhiling，Zeng Jianping.New tracking-control strategy for airbreathing hypersonic vehicles［J］.Journal of Guidance，Control and Dynamics，2013，36（3）:846-859.

［4］ Qin Changmao，Qi Naiming，Li Rui，et al.ADRC fractional order PID controller design of hypersonic flight vehicle［J］.Transactions of Nanjing University of Aeronautics&Astronautics，2011，28（3）:240-245.

［5］ Eusuff M M，Lansey K E.Water distribution network design using the shuffled frog leaping algorithm［C］∥World Water Congress.［S.l.］:American Society of Civil Engineers，2001.

［6］ Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm［J］.Journal of Water Resource Planning and Management，2003，129（3）:210-225.

［7］ Eusuff M M，Lansey K E，Pasha E.Shuffled frogleaping algorithm:A memetic meta-heuristic for discrete optimization［J］.Engineering Optimization，2006，38（2）:129-154.

［8］ Ahandani M A，Morteza Alinia.A diversified shuffled frog leaping:An application for parameter identification［J］.Applied Mathematics and Computation，2014，239:1-16.

［9］ Darvishi A，Alimardani A，Vahidi B，et al.Shuffled frog-leaping algorithm for control of selective and total harmonic distortion［J］.Journal of Applied Research and Technology，2014，12:111-121.

［10］Arshi S S，Zolfaghari A，Mirvakili S M.A multi-objective shuffled frog leaping algorithm for in-core fuel management optimization［J］.Computer Physics Communications，2014，185（10）:2622-2628.

［11］Behdad A，Rahmat-Allah H，Eskandar G.Decreasing activity cost of a distribution system company by reconfiguration and power generation control of DGs based on shuffled frog leaping algorithm［J］.International Journal of Electrical Power&Energy Systems，2014，61:48-55.

［12］Zhu Guangyu，Zhang Weibo.An improved shuffled frog-leaping algorithm to optimize component pickand-place sequencing optimization problem［J］.Expert Systems with Applications，2014，41（15）:6818-6829.

［13］Zhen Ziyang，Wang Zhisheng，Gu Zhou，et al.A novel memetic algorithm for global optimization based on PSO and SELA［C］∥Proceedings of Advances in Computation and Intelligence，ISICA 2007.［S.l.］: Springer，2007，4683:127-136.

［14］Zhen Ziyang，Wang Daobo，Liu Yuanyuan.Improved shuffled frog leaping algorithm for continuous optimization problem［C］∥IEEE Congress on Evolutionary Computation.Trondheim，Norway:［s.n.］，2009:2992-2995.

（Executive editor:Zhang Tong）

*Corresponding author:Zhen Ziyang，Associate Professor，E-mail:zhenziyang@nuaa.edu.cn.

How to cite this article:Liang Bingbing，Jiang Ju，Zhen Ziyang，et al.Improved shuffled frog leaping algorithm optimizing integral separated PID control for unmanned hypersonic vehicle［J］.Trans.Nanjing U.Aero.Astro.，2015，32（1）:110-114.

http://dx.doi.org/10.16356/j.1005-1120.2015.01.110

（Received 4 November 2014；revised 6 January 2015；accepted 12 January 2015）

TP273；O321 Document code:A Article ID:1005-1120（2015）01-0110-05