神经网络预测控制在污水处理溶解氧控制中的应用

张学阳，项雷军，林文辉，郭新华

（1.华侨大学 信息科学与工程学院，福建 厦门361021；2.泉州市益源环保设备有限公司，福建 泉州362021）

20世纪40年代，国外学者就已开始研究污水处理模型，先后开发出一些简化的活性污泥法模型.1987年，国际水质协会（IAWQ）在前人研究的基础上推出了活性污泥1号模型（ASM1），ASM1是活性污泥模型发展的里程碑，成为模拟活性污泥系统的强有力工具［1］.溶解氧（DO）浓度是活性污泥法污水处理曝气过程中重要的运行控制参数［2－3］，在很大程度上影响着出水水质.因此，研究溶解氧浓度控制有着重要的意义和应用价值.近年来，国内外学者对此做了较为深入的研究，提出了一系列的溶解氧浓度控制方法［4］，如PID 控制［5］、模糊控制［6］、神经网络控制［7］以及结合前三种方法的优点所提出的综合方法［8－10］，此外还有模型预测控制［11－12］、遗传算法［13－14］等.在满足出水水质要求下，上述方法基本上能对溶解氧浓度进行控制，有效跟踪溶解氧浓度设定值.但是仍存在一些问题，诸如控制模型受限制前提条件较为苛刻，或仅能实现溶解氧恒定设定值的跟踪控制，或较少考虑实际过程中外界因素对系统的干扰.综合神经网络控制和预测控制两种方法的优点，基于活性污泥法ASM1标准模型，本文提出一种污水处理溶解氧浓度的神经网络预测控制器（NNPC）设计方法，在考虑溶解氧测量白噪音干扰和进水流量发生阶跃变化情况下，有效实现溶解氧浓度的时变设定值跟踪控制.

图1 活性污泥法污水处理工艺流程Fig.1 Schematic representation of the activated sludge sewage treatment process

1 污水处理系统模型的建立

活性污泥法污水处理工艺流程，如图1所示［1－2］.由图1可知：系统主要由曝气池、曝气系统、沉降池、污泥回流系统和剩余污泥排放系统组成.生化曝气池是一个混合有液体和固体悬浮物的生物反应器；沉降池是一个利用重力沉降法将污泥从废水中分离的澄清槽，去除的污泥一部分回流到曝气池中，剩余一部分污泥被排放出去［2］.

分析活性污泥法污水处理工艺流程，采用ASM1作为控制对象，建立污水处理过程数学模型［3］为

式（1）～（4）中：输入变量KLa为氧气传递系数，利用KLa描述曝气过程，KLa和曝气量W（t）成正比例关系；X（t）为微生物质量浓度；S（t）为底物质量浓度；Xr（t）为回流污泥质量浓度；输出变量DO（t）为溶解氧质量浓度；β，r为反应速率系数；Y为表现产率系数；Sin，DOin分别为输入底物浓度和输入溶解氧浓度；DOs为溶解氧饱和浓度；Kc为常数.

微生物量增长速率为

式（5）中：μmax是最大反应速率；Ks，Ko分别是与底物的质量浓度、溶解氧的质量浓度有关的常数.

式（1）～（5）中各参数的取值规定如下：Y＝0.65；μmax＝0.15h－1；α＝0.018；β＝0.2；r＝0.6；Kc＝0.5；Ko＝2mg·L－1，Ks＝100mg·L－1；Sin＝200mg·L－1；DOin＝0.5mg·L－1；DOs＝10mg·L－1；D（t）＝0.1h－1；W＝80·h－1.变量初始化值如下：X（t）＝200mg·L－1；S（0）＝88mg·L－1；Xr（0）＝88mg·L－1；Xr（0）＝320mg·L－1；DO（0）＝0mg·L－1.

2 溶解氧神经网络预测控制器的设计

神经网络具有通过学习逼近任意非线性映射的能力.将神经网络应用于污水处理过程这类典型非线性系统的建模与辨识，建立污水处理过程的输入输出模型，可不受非线性模型类的限制，且便于给出工程上易于实现的学习算法［15］.模型预测控制（MPC）具有3个基本特征：预测模型、滚动优化、反馈校正.MPC是一种典型的约束优化控制方法，在复杂工业过程控制中应用广泛［16］.但由于模型预测控制方法需要建立被控对象的精确数学模型，且预测模型的精度对模型预测控制器的性能有较大影响，故该方法在非线性系统控制中的应用受到限制.

由于污水处理过程具有严重的时滞性、非线性和不确定性.先利用BP神经网络对系统进行辨识，建立预测控制器的逼近模型；再设计神经网络预测控制器，通过滚动优化目标值，最终实现溶解氧浓度的时变设定值跟踪控制.污水处理过程中，溶解氧的神经网络预测控制系统结构，如图2所示.其中包括神经网络预测模型和神经网络预测控制器，神经网络预测模型使用过去时刻的输入u（k＋p－nu），…，u（k＋p）和输出y（k＋p－ny），…，y（k＋p－1）数据，通过性能指标函数Jm（k）训练网络，并用训练好的神经网络逼近模型预测系统未来输出，神经网络预测控制器通过最小化误差代价函数Jc（k）计算Δu（k），与前一时刻控制量u（k－1）相加得到此刻控制量最优输入KLa，从而控制输入在未来一段指定时间内将最优化模型性能，使系统实际输出y（k）不断接近期望输出值yr.

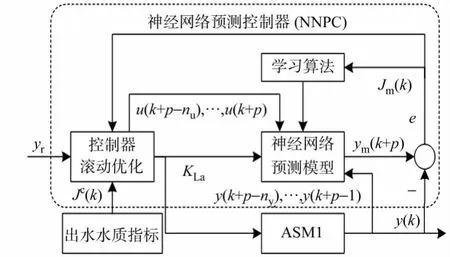
图2 神经网络预测控制系统结构框图Fig.2 Structure of neural network predictive control system

2.1 神经网络预测模型

利用神经网络辨识系统模型，设该系统可用离散时间模型描述为

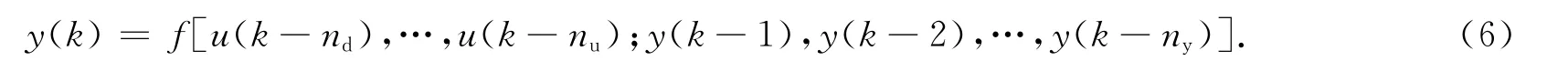
式（6）中：y（k）为系数期望输出值；nd为系统滞后拍数；nu为用于辨识模型的过去时刻输入量个数；ny为用于辨识模型的过去时刻输出量个数；f（·）为非线性拟合函数.利用递推原理，根据模型（6）可以预测k＋1时刻输出值，将得到的k＋1时刻的预测值作为预测模型预测k＋2时刻的输入，重复使用此模型进行前向多步预测，预测下一步时，将之前的预测结果作为预测下一步的输入.根据模型（6）可以预测k＋p时刻的系统输出值为

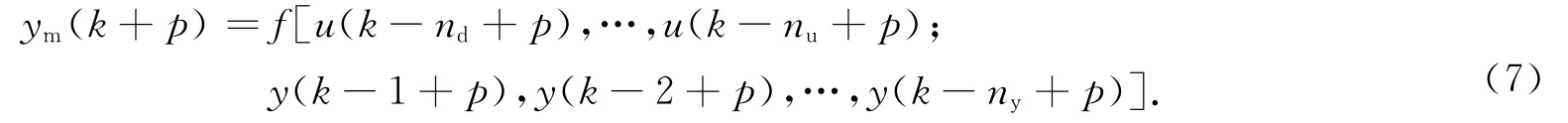
采用三层BP神经网络训练f（·），包括输入层（i个神经元）、隐含层（j个神经元）和输出层（h个神经元），建立神经网络模型为

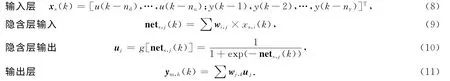
式（8）～（11）中：xs，i（k）为输入层第i个神经元的输入；nets，j（k）为隐含层第j个神经元的输入；uj为隐含层第j个神经元的输出；ym，h（k）为输出层第h个神经元的输出；g（·）为隐含层传输函数，这里取S型函数；wi，j为输入层第i个神经元到隐含层第j个神经元的连接权值；wj，k为隐含层第j个神经元到输出层第k个神经元的连接权值.

BP神经网络在辨识过程中根据输出量误差按照梯度修正法修正权值，修正权值的过程为

式（13），（14）中：η为预测模型学习率，η＞0.

通过神经网络的不断学习更新权值，使预测输出值不断接近实际输出值.由以上分析可得，k＋p时刻的神经网络学习模型为

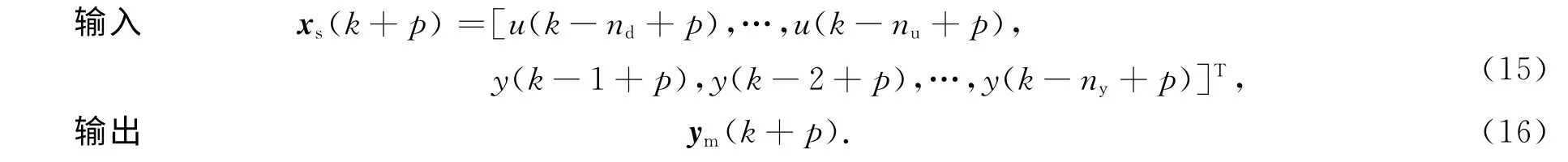
式（15）中：u（k），u（k＋1），…，u（k－nd＋p）等参数，用NNPC的预测值代替，如果超出预测范围，则以最后的预测值代替.

训练神经网络的数据来源于污水处理数学模型（1）～（4）.通过实验可得：当输入在［0.45，0.95］内时，输出量即溶解氧浓度可以维持在［1.58，3.97］内，神经网络初始的学习样本通过在给定区间［0.45，0.95］内随机输入并测定相应输出的方式获得.考虑不同单位的数量级差异，在训练网络之前，所有数据均须被归一化处理至区间［0，1］，然后用处理后的数据训练神经网络.

通过以上分析，系统辨识只需要建立一个神经网络，根据系统过去时刻的输入输出数据，通过训练建立系统的单步预测模型，根据式（6），（7），将多个单步模型串联即可获得多步预测模型.

2.2 神经网络预测控制器

采用三层BP网络建立神经网络预测控制器，神经网络预测控制器模型的输入和输出分别为

式（17）～（18）中：yr（k）为期望输出值；nc为控制时域长度.

神经网络预测控制器模型为

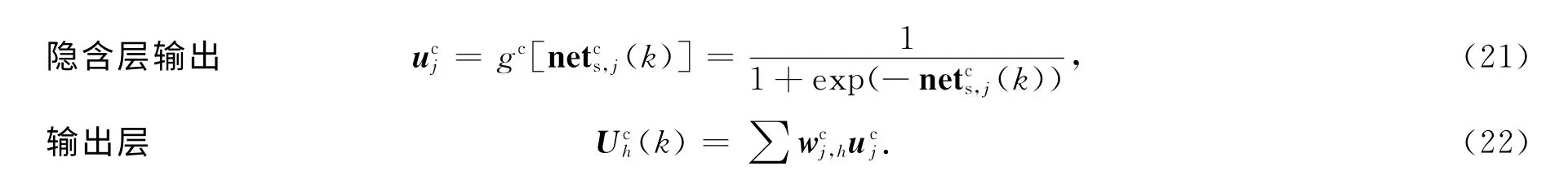
式（19）～（22）中：xcs，i（k）为输入层第i个神经元的输入，i＝1，2，…，ny＋p＋1；netcs，j（k）为隐含层第j个神经元的输入；ucj为隐含层第j个神经元的输出，j＝1，2，…，nc，j；Uch（k）为输出层第h个神经元的输出，h＝1，2，…，nc，h；gc（·）为隐含层S型传输函数；wci，j为输入层第i个神经元到隐含层第j个神经元的连接权值；wcj，h为隐含层第j个神经元到输出层第h个神经元的连接权值.

权值更新的方式为

式（23）～（24）中：ηc为控制器学习率，ηc＞0.

在实际污水处理系统中，出水水质是最重要的污水处理指标，而排出的底物浓度是出水水质是否达标的主要检测指标.研究表明，溶解氧浓度控制在1.58～3.97mg·L－1之间，能够满足每日排出的底物浓度不大于150kg BOD 的环保要求［10］.因此，研究的溶解氧浓度控制值均约束在此范围内.考虑上述约束条件，建立神经网络预测控制器，最小化性能目标代价函数Jc（k），即

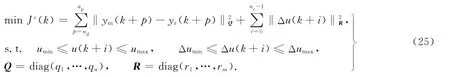
式（25）中：Q为误差权矩阵；R为控制权矩阵；np为预测时域长度；nc为控制时域长度.应用预测控制器（25）来计算Δu（k），与前一时刻控制量u（k－1）相加得到此刻控制量最优输入KLa，从而输入控制量在未来一段指定的时间内将最优化模型性能，使系统实际输出y（k）不断接近期望输出值yr.

3 控制系统的仿真分析

以基于活性污泥法ASM1模型为被控对象，在Matlab／Simulink仿真环境中构建污水处理溶解氧神经网络预测控制系统.在仿真过程中，根据实际情况假设：系统连续运行5d（即120h）内，溶解氧的时变设定值为先由2.0mg·L－1升高到2.5mg·L－1，再恢复到2.0mg·L－1，接着降低到1.7mg·L－1，最后再恢复到2.0mg·L－1.控制系统采样时间t取为0.1h；神经网络预测控制器的预测时域长度np＝10；控制时域长度nc＝3，滞后拍数nd＝0，nu＝2，ny＝2；神经网络预测模型选择4－6－1结构，神经网络预测控制器选择2－5－1结构；神经网络学习速率为η＝0.2，ηc＝0.5.

3.1 测量白噪音情况下时变设定值的跟踪控制

假设在溶解氧浓度传感器反馈信号中加入幅值为0.01的高斯白噪音干扰信号，分别采用传统PID控制器和神经网络预测控制器对系统溶解氧浓度（ρDO）进行控制仿真，得到的仿真结果如图3所示.由图3分析可知：在测量白噪音干扰下，传统PID 控制器出现持续振荡现象，即溶解氧浓度控制波动幅度较大，而神经网络预测控制器对溶解氧浓度的时变设定值跟踪控制超调量小，溶解氧浓度跟踪控制能够保持平稳状态，可有效实现对溶解氧浓度的时变设定值跟踪控制.

3.2 进水流量发生阶跃变化情况下时变设定值跟踪控制

假设系统在30h时给进水底物质量浓度（Sin）加入大小为50mg·L－1的阶跃干扰，在80h时给Sin加入大小为－100mg·L－1的阶跃干扰，在系统控制器各参数均保持不变的前提下，分别采用传统PID控制器和神经网络预测控制器对系统溶解氧浓度（ρDO）进行控制仿真，得到仿真结果如图4所示.由图4分析可知：在进水流量发生阶跃干扰下，神经网络预测控制器对溶解氧浓度的时变设定值跟踪控制引起的超调量小，且能较快恢复到稳定状态，而传统PID 控制器则出现较大超调量.

图3 测量白噪音情况下的仿真结果Fig.3 Simulation results with white noises in the DO concentration measurements

图4 进水流量发生阶跃变化情况下的仿真结果Fig.4 Simulation results with step disturbances in the influent

3.3 控制性能的量化比较

由图3和图4可以明显看出：对于溶解氧浓度的时变设定值跟踪控制，与传统PID 控制器相比较，神经网络预测控制器调节时间短、超调量较小，动态响应速度快，显示了该控制器的有效性和优越性.采用IAE，ISE作为两个积分型性能指标来对控制性能进行测试与量化评价，它们分别定义为

通常较小的IAE或ISE指标代表更好的控制性能.性能指标量化结果，如表1所示.由表1可知：在不同干扰情况下，神经网络预测控制方法相比于传统PID 控制方法，IAE 和ISE 指标均分别有较大幅度的减小，系统控制性能得到有效改进.

表1 不同控制方法系统性能的比较Tab.1 Comparisons of system performance for different control methods

4 结束语

基于活性污泥法污水处理ASM1模型，考虑若干约束条件，设计出神经网络预测控制器，有效实现了污水处理过程溶解氧浓度的时变设定值跟踪控制，并研究了溶解氧浓度传感器测量白噪音和进水流量发生阶跃变化两种干扰情况对溶解氧浓度跟踪控制性能的影响.仿真实验结果表明：针对污水处理溶解氧浓度的时变设定值跟踪控制，考虑外界干扰因素，与传统PID 控制器相比，神经网络预测控制器超调量减小，响应快速，明显改善了系统动态控制性能，抑制干扰能力增强，有良好的自学习能力和适应性，为解决污水处理溶解氧浓度时变设定值跟踪控制问题提供了一条很好的途径.

［1］HENZE M.Activated sludge models ASM1，ASM2，ASM2dand ASM3［M］.London：IWA Publishing，2000：13－15.

［2］KATEBI M R，JOHNSON M A，WILKE J.Control and instrumentation for wastewater treatment plant［M］.London：Springer－Verlag，1999：38－41.

［3］NEJJARI F，BENHAMMOU A，DAHHOU B，et al.Non－linear multivariable adaptive control of an activated sludge wastewater treatment process［J］.Int J Adapt Control Signal Process，1999，13（5）：347－365.

［4］张平，苑明哲，王宏.基于国际评价基准的溶解氧控制方法研究［J］.信息与控制，2007，36（2）：199－203.

［5］TZONEVA R.Optimal PID control of the dissolved oxygen concentration in the wastewater treatment plant［C］∥IEEE AFRICON Conference.Windhoek：IEEE Press，2007：1－7.

［6］CHEN J C，CHANG Ni－bin.Mining the fuzzy control rules of aeration in a submerged biofilm wastewater treatment process［J］.Engineering Applications of Artificial Intelligence，2007，20（7）：959－969.

［7］甄博然，韩红桂，乔俊飞.基于增长型神经网络的污水处理过程溶解氧控制［J］.中南大学学报：自然科学版，2009，40（1）：74－79.

［8］王小艺，李万东，刘载文，等.一种模糊PID－Smith污水处理的控制方法［J］.计算机与应用化学，2010，27（6）：801－803.

［9］付文韬，武利，王莉莉，等.神经网络PID 的溶解氧控制系统［J］.计算机与应用化学，2013，30（10）：1135－1138.

［10］胡玉玲，曹建国，乔俊飞.活性污泥污水处理系统的模糊神经网络控制［J］.系统仿真学报，2005，17（10）：2541－2544.

［11］SHEN Wen－hao，CHEN Xiao－quan，PONS M N，et al.Model predictive control for wastewater treatment process with feedforward compensation［J］.Chemical Engineering Journal，2009，155（1／2）：161－174.

［12］CRISTEA S，DEPRADA C，SARABIA D，et al.Aeration control of a wastewater treatment plant using hybrid NMPC［J］.Computers and Chemical Engineering，2010，35（4）：638－650.

［13］刘载文，张春芝，王小艺，等.基于遗传算法的污水处理过程优化控制方法［J］.计算机与应用化学，2007，24（7）：959－962.

［14］HOLENDA B，DOMOKOS E，REDEY A，et al.Aeration optimization of a wastewater treatment plant using genetic algorithm［J］.Optimal Control Applications and Methods，2007，28（3）：191－208.

［15］孙增圻，张再兴，邓志东.智能控制理论与技术［M］.2版.北京：清华大学出版社，2011：123－126.

［16］CAMACHO E F，BORDONS C.Model predictive control.advanced textbooks in control and signal processing［M］.2nd.London：Springer－Verlag，2004：3－9.