基于需求响应的实时电价研究综述

黄海新 邓 丽 张 路

（1. 沈阳理工大学信息科学与工程学院，沈阳 110159；2. 中国科学院沈阳自动化研究所，沈阳 110016）

近年来，随着用户用电需求的增加，传统的电网面临着许多存在或者潜在性的问题，电网的有效性与可靠性受到威胁。同时，新能源产品（如混合动力电动汽车等）的出现、分布式发电装置的应用，也对用户的用电行为产生显著影响。峰值电耗的增加使现有电网处于高负荷状态，影响了整个电网的性能。相对于增加发电厂的发电量来满足用户的需求，智能电网的需求响应成为处理上述问题的关键。而实时电价策略，作为需求响应的重要措施之一，是解决智能电网用电问题的关键技术。本文介绍了智能电网的需求响应和实时电价策略，并从供电侧与用户侧的供需角度，对国内外电网实时电价的研究与发展情况进行了综述。

1 需求响应

随着经济与社会的发展，电力产业不断贯穿于人们的生产、生活等各个领域，各个行业对电力的需求不断增加，因此，电力产业对可持续发展战略起着至关重要的影响作用，智能电网孕育而生。智能电网不同于传统的电网模式，只存在单一的能量与信息流，智能电网中存在双向的能量与信息流，实现用户与电网的衔接与互动。需求响应，则是解决智能电网中理想供需水平的机制。

需求响应，即电力需求响应的简称，是指当电力批发市场价格升高或电力系统的有效性和可靠性受到威胁时，电力用户在接收到供电商发出的诱导性减少负荷的直接补偿通知或者电力价格上升信号后，改变其固有的用电行为模式，从而减少或者推移某时段的用电负荷而响应电力供应，保障电网稳定，并抑制电价上升的短期行为。它是需求侧管理（Demand-Side management，DSM）的解决方案之一。美能源部报告[1]中详细指出，需求响应最显著的作用体现在电力生产中能源效率的提高。具体作用体现如下[2]：

1）用户对激励型或者价格型电力需求做出响应，降低用户用电成本。

2）减少用户用电高峰期需求，有效地避免或减少在基础电力设施升级、新建方面需要投入的巨大成本，减少电力成本快速增长。

3）用户自主决定消费的时间与数量，减弱发电厂商的市场力，改善电力市场运行效率。提供电力市场的辅助服务，提高电力系统的安全性。

4）能够降低线损率，带来节能减排的效益。

在需求响应的分类问题上，美国能源部的报告[1]最具代表性。其中指出需求响应的两种分类方式：激励型需求响应和价格型需求响应[2]，如图 1所示。

图1 需求响应分类

1）激励型需求响应

所谓激励型需求响应（Intensive-Based Programs，IBP），是指为了避免电力系统出现紧急情况，电力部门或系统运营商采用奖励的策略在需求高峰期对电力用户的负荷进行直接或间接的控制或干扰，激励用户的用电行为以降低在该时段的负荷需求，并对其控制或干扰行为进行补偿。激励型需求响应可分为：直接负荷控制，可干扰负荷控制，需求侧竞价，紧急需求响应，容量市场计划，辅助服务市场计划。

2）价格型需求响应

所谓价格型需求响应（Pricing-Based Programs，PBP），就是通过人为或者市场自发地调整电价来反映供电成本的时段差异，用户进而做出用电时间与方式的调整。具体来说，价格型需求响应就是通过用户在较高价格的高峰期减少用电，在较低价格的非高峰期增加用电（弥补之前的用电削减）来平缓负荷曲线，增强用户对价格的响应能力，并提高系统稳定性。参与此类项目的电力用户可以直接降低高峰期负荷需求或是将部分高峰期用电转移到非高峰期。价格型需求响应可分为：分时电价，关键峰荷电价，实时电价。

2 实时电价

电价的计算方式有多种，主要的方法有综合成本法、长期边际成本法和短期边际成本法[3]。在工程上，短期边际成本法又可称为“实时电价”。

实时电价的概念最早是由美国F. C. Schweppe教授在20世纪80年代提出，是配电市场需求响应的最理想电价机制之一[4]。不同于传统的单一电价模式，实时电价，通常是在考虑运行成本和基本投资的情况下，在给定时段向用户提供电能的边际成本。狭义的实时电价是在得到用户的用电情况后，然后再根据用电情况来确定用户的用电价格。实际应用中，我们不可能在得到用户某时段电耗后，再决定该时段的用户电价，这样既不能降低用户的电耗，也不能减少供电商的发电量，体现实时电价的初衷。因此，广义的实时电价是指用户在电价发布前的一天或前几个小时得到实时电价。最典型的实时电价类型是用户提前一天得到用电价格，即用户已知下一个24h的电力定价情况。实际上，实时电价的确定不仅要满足成本的需求，同时应满足电量的平衡、发电功率及线路功率等约束。对于第K个用户在时段 t内的实时电价可以看作以下各组成部分的和：

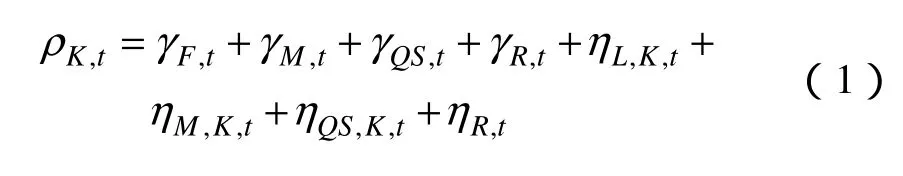
式中，ρK,t为第K个用户在时段t的实时电价，γF,t为边际发电燃料成本，γM,t为边际发电维护成本，γQS,t为发电质量分量，γR,t为发电收支平衡项，γL,K,t为边际网损成本，ηM,K,t为边际网损维护成本，ηQS,K,t为网络供电质量分量，ηR,t为网络收支平衡项。

实时电价，作为需求响应的重要策略之一，在如今的智能电网中有着较为广泛的应用。其通过动态地跟踪整个电力市场的价格模式，引导用户避开用电高峰期的用电行为，降低用户在高峰期的负荷。在实现节能减排，减少电力投资，降低负荷需求，实现供需平衡等问题上，都具有重大意义[5]。

3 实时电价算法的国内外研究现状

在智能电网时代，随着通信网络技术的普及与完善，仅单一的考虑发电商的定价策略早已不能满足电力应用的有效性与可靠性要求。智能电网的快速发展与智能电表的广泛应用使得用户与电网各领域的信息交互越发频繁。用户端负荷，特别是弹性负荷有组织、有选择、有计划的接入电网成为用户的智能需求。实时电价成为当前智能电网技术的研究热点，结合大数据分析、机器学习等先进方法，实现更精确的实时电价的操作性与实用性已成为现实。

实际研究过程中，越来越多的学者将智能电网划分为不同的领域，如发电侧、供电侧、用户侧等。而传统的电网重发电轻用电的模式早已不能适应智能电网发展的大趋势。因此，用户侧的智能电网研究日趋成为近几年研究的重点。现有的研究中，多数学者从用户侧与供电侧角度提出了实时电价策略的模型与算法。下面我们将从供电侧与用户侧的供需水平出发，介绍现有的实时电价算法。

3.1 基于能耗调度理论的实时电价算法

2008年，美能源部的报告明确指出，国家电力消耗的74%来自于建筑物。这就相当于所有部门的总能耗的39%。而大部分建筑物电耗的低效性，导致了数十亿资金的浪费与多余温室气体的排放[6]。因此，能耗调度成为电价制定的关键问题。

Mohsenian-Ra等提出了基于能耗调度理论的最优实时定价算法。该算法将获得最少的电能成本及峰平比作为目标函数，根据博弈论思想，采用内点法求解问题，得到每个用户的最优能耗调度方案，降低了总电能成本及峰平比[7]。在缺乏用户对可变电价的反馈信息及有效的建筑自动化系统的条件下，Mohsenian-Ra又提出了一种自治住宅能耗调度框架，实现了在与带有倾斜块率（inclining block rates）结合的实时定价策略下，建立用户在所付电费最小和操作用电器的等待时间最短之间折中的模型，基于线性规划，同样采用内点法解决该最优化问题，但算法的收敛速度慢[8]。

随着新能源的发现与应用，混合能源电力设备的普及，相比与传统的用电模式，用户侧的用电结构发生巨大变化。考虑到能源价格、可再生能源、温度及用户能源需求情况等信息及电力汽车（EVs）的应用对用户用电行为的影响，Juan M.Lujano-Rojas等给出了利用智能电网的通信基础设施得到的住宅用户的最优能耗调度策略，实现了供电商与用户的协调，即用户获得电器及电力汽车的最优利用方案。算法从用户侧考虑，实现用户电耗的可控性，能使用户获得适合于自身消费水平的实时电价[9]。

3.2 基于统计需求弹性模型的实时电价算法

电力市场的主要作用是通过对电力系统中发、输、供、用等各个环节组织协调与管理，达到社会效益的最优化。电价是体现管理思想的最佳工具。因此，电力市场中的电价模型应正确反应出用户侧与供电侧的效益。国内外很多学者在用户侧与供电侧的总体效益最大化的实时电价模型问题上进行了研究。

随着各企业推出包括能源管理中心、通信网络和远程数据采集单元三级物理结构的能源管理系统，为用户提供能源自动化、能耗监测、能耗计量、能效分析与管理等功能。我们可以获得电力负荷使用及实时电价信息，并根据所得信息引导用户电耗以获得用户的最优效益[10]。基于所得的交互信息，Rongshan等学者应用效用理论，对电力市场的需求价格弹性进行研究。文献将用户所需负荷函数表示为电价的函数，将用户的效用函数定义为多维的价格需求曲线。同时把社会效益最大化作为最优实时电价问题的目标函数。在不要求用户与供电商过多信息交换的前提下，通过迭代算法，得到用户与供电商的总体效益最大化[11]。

电力市场的开放性使用户面临着越多的可变电价政策，用户可以通过改变需求来降低自身电耗。因此，Daniel S. Kirschen等提出了考虑到需求弹性的定价方法。用自弹性与互弹性矩阵对用户的用电行为进行建模，弹性影响的计算随着调度策略与计算价格不断迭代。通过拉格朗日松弛算法来计算每一次调度安排，并根据英格兰和威尔士的电力库规则完成电力价格的实际制定[12]。

3.3 基于效益模型的实时电价算法

与基于统计需求弹性模型的实时电价算法相似，基于效益模型的实时电价算法同样是实现用户端与供电端的双方效益最大化。

对于单供电商多用户模型，Corentin Evens SK通过实时电价信息来调整用户能耗，采用滚动窗计算周期内能耗，并采用线性规划求解。但滑动窗的结构决定着窗外数据默认为零，不能很好的保留数据，因此会产生较大误差[13]。Pedram Samadi等建立了基本的能耗调度模型，通过分布式算法实现在总电耗低于产电量的基础上最大化用户总效用，并且最小化能源供应商的费用，给出了基于对偶分解的次梯度算法，在未给出用户负载的类型参数的基础上，算法以公平有效的方式获得每个用户的最优能耗[14]。

由于负载类型的多样化，在文献[14]的基础上，Poramate Tarasak分析了三种不确定的负载模型：有界不确定性模型（Bounded Uncertainty Model），高斯模型（Gaussian Model）和分布未知的模型（Unknown Distribution Model），发现负载的不确定性会影响最优定价，并造成其增高，且分布未知的模型比高斯模型有更高的最优定价。仿真结果表明算法实现了不同负载下用户的最低能耗[15]。为达到供需平衡，减少整体能耗，Jie Yang提出了基于供需匹配的电力控制与实时电价方法，并同时提出依赖用户自身策略及其他消费者消费策略的效用函数模型，分布式算法实现模型最优化[16]。Asadi提出了基于PSO的效用函数最大化算法，协同工作的实时定价策略使每个用户的能耗最低进而达到所有用户的最大效用。文献同时比较了RTP与TOU两种不同定价策略。给出了用户基于RTP的电耗模式[17]。

对于多供电商多用户模型，S. Weckx等提出了在不违反网络约束条件下，应用于三相四线径向网络中的实时定价算法，在不共享用户个人信息的基础上，使不同的能源提供者共享同一网络，最终得到在具有网络约束的不平衡配电网中的实时价格策略[18]。

3.4 基于阻塞管理的实时电价算法

基于阻塞管理的实时电价，通过处理电网负荷拥塞来获得供电与用电的平衡。传统的解决电网阻塞的方法是拥塞价格法。所谓的拥塞价格法，是将联络线的价格信号传递给市场参与者，来鼓励发电商在价格高的区域兴建电厂，以减少阻塞。为了保证用户服务质量，网络共享带宽问题成为了近年来研究的重点。而在用户与应用巨大差异的情况下，问题的难点就在于对用户进行约束。Ayalvadi Ganesh等学者基于上述原因，将问题从网络转化到用户终端，提出了用户适应与动态学习的分布式方案，采取拥塞价格机制来获得用户侧的最大效益。该算法在提高用户自身的用电满意度时，忽略了供电商的利益。且算法受参数影响较大，收敛性较差[19]。实际中，仅作用于终端的实时电价策略并不能很好地反映整个电网的性能，此时的拥塞价格不能对传输系统控制器进行正确的激励。拥塞价格与电网建设并没直接联系，它只单方面考虑了阻塞线路的价格，并不能保证最有效的电力使用。因此，研究者提出了解决网络堵塞管理问题的节点边际电价（Locational Marginal Pricing，LMP）策略，从整个电网出发分析问题，被认为是衡量电能价值的一种定价方式[20]。节点边际电价，是指某一节点增加1MW的负荷，系统向该节点供应电能的边际（或微增）成本，这与实时电价有相同的含义。Luonan Chen等对LMP的组成进行了详细地分析，将影响LMP的因素分为发电装置、输电阻塞、电压限制等方面。利用LMP分析价格的各影响因素，对电网进行拥塞管理，提高电网的有效利用率[21]。

文献[22]对国内外阻塞管理及节点边际电价的理论研究和实际应用进行总结、评述，并根据国内电力市场特点，对阻塞管理和节点边际电价进行了深入地研究，推导出节点边际电价与阻塞线路影子价格的关系。并以直流最优潮流为核心，提出了交直流迭代求解含网损的节点边际电价计算方法。同时提出了全时段优化的节点边际电价计算模型[22]。

4 实时电价策略下用户用电行为分析

实时电价策略的实施必然对用户的用电行为产生影响，用电行为同时又影响着实时电价的制定。因此，对用户用电行为学习，是设计有效可行的实时电价策略的关键。当前的大多数研究主要是在于理解实时电价的经济作用及用户的集中反应[23-25]。而用户对价格的反映可以将其分为价格敏感型用户及价格激励型用户，用户级响应及家电级响应。因此，Fan-Lin Meng等，将家电分为不可转移电器（Non-Shiftable Appliances）、可转移电器（Shiftable Appliances）及季节性或可断电器（Curtailable Appliances），提出了实时电价下不同类型家电的电耗模式的学习模型：应用于可转移家电的基于平均价格排序的学习模型，应用于季节性或可断电器的多元线性回归学习模型。从家电级视角分析了实时电价对用户用电行为的影响[26]。

由于智能家电的普及，电价策略的改变，Sebastian gottwalt等提出了在恒定电价下用户负载曲线的仿真模型，并估算了在智能家电及基于时间的价格策略下用户负载曲线的变化，研究了智能家电及可变价格策略对电价的影响。结果表明在新的价格策略下电力公司会面临新的需求高峰，用户需要改变大量的家用电器的用电模式来实现供需匹配，达到全局最优[27]。

5 结论

随着社会的进步，科技的发展，智能电网早已取代了传统的电网模式。现代电力市场条件下，需求响应成为缓解电力市场中的供需矛盾，降低峰值负荷，实现节能减排的重要工具之一[28-29]。实时电价作为价格型需求响应的一种，在现实电网中起着至关重要的作用。本文从用户侧与供电侧的供需水平出发，分析了几种现有的实时电价模型与算法：基于能耗调度理论的实时电价算法，基于统计需求弹性模型的实时电价算法，基于效益模型的实时电价算法及基于阻塞管理的实时电价算法。而合理的分析实时电价策略下用户的用电行为，根据用户响应制定公平有效的实时电价策略[30]，则会进一步改善当今电网的使用现状，提高智能电网的性能与核心竞争力。

传统单一的电价模式，着重于从供电商出发，不考虑用户侧的反应制定电价，不存在用户与电网之间的信息交流。现有的实时电价是一种响应电价，是在用电信息充分采集的前提下，电网根据用户的用电信息制定电价，进而影响用户的用电行为。在智能电网中，可以获得足够的电网数据，基于大数据分析的实时电价软计算智能算法未尝不是电网发展的趋势。同时，为了实现电网各成员获利，博弈仍是实现需求响应的实时电价策略的不错选择。博弈的多方可在最优定价策略下同时获得各自的最大效益。用户，作为智能电网数量最多的成员，承载着电网的应用，对系统有着直接切身利益的要求。随着新能源的产生，各种分布式发电装置的应用[31]，家用电器的多样化，用户的用电要求也随之越来越高。因此，满足电网各成员的最优获利，涉及用户质量需求的实时电价设计，提高用户服务质量，会成为发展与完善实时电价算法的趋势。

[1] US Department of Energy, BENEFITS OF DEMAND RESPONSE IN ELECTRICITY MARKETS AND RECOMMENDATIONS FOR ACHIEVING THEM. A REPORT TO THE UNITED STATES CONGRESS PURSUANT TO SECTION 1252 OF THE ENERGY POLICY ACT OF 2005 (FEBRUARY 2006)[2014-01-05] [EB/OL].

[2] 陶小马, 周雯. 电力需求响应的研究进展及文献述评[J]. 北京理工大学学报(社会科学版), 2014, 16(1):32-40.

[3] 曲家余. 面向智能电网的基于梯度投影法的实时电价算法研究[D]. 沈阳: 东北大学, 2013.

[4] 雷霞, 刘俊勇, 党晓强. 配电市场购售电优化模型研究综述[J]. 电力系统保护与控制, 2010, 38(2):136-145.

[5] 毕超. 基于功率分解理论的用户实时电价研究[D].北京: 华北电力大学, 2008.

[6] U.S. Department of Energy, 2008 Buildings Energy Data Book[R]. Energy Efficiency and Renewable Energy, Mar. 2009.

[7] Mohsenian-Rad A H, Wong V, Jatskevich J, et al.Optimal and autonomous incentive-based energy consumption scheduling algorithm for smart grid[C]//Innovative Smart Grid Technologies (ISGT), 2010,2010: 1-6.

[8] Mohsenian-Rad A H, Leon-Garcia A. Optimal residential load control with price prediction in Real-Time electricity pricing environments[J]. Smart Grid, IEEE Transactions on, 2010, 1(2): 120-133.

[9] Lujano-Rojas J M, Monteiro C, Dufo-Lopez R A.Optimum residential load management strategy for real time pricing (RTP) demand response programs[J].Energy Policy, 2012, 45(2): 671-679.

[10] 张延宇, 曾鹏, 臧传治. 智能电网环境下家庭能源管理系统研究综述[J]. 电力系统保护与控制, 2014,42(18): 144-154.

[11] Yu Rongshan, Yang Wenxian, Rahardja S. Optimal real-time price based on a statistical demand elasticity model of electricity[C]//Smart Grid Modeling and Simulation (SGMS), 2011 IEEE First International Workshop on, 2011: 90-95.

[12] Kirschen D S, Strbac G, Cumperayot P, et al. Factoring the elasticity of demand in electricity prices[J]. Power Systems, IEEE Transactions on, 2000, 15(2): 612-617.

[13] Evens S K C, Kärkkäinen S. Pricing models and mechanisms for the promotion of demand side integration[J]. VTT Technical Research Centre of Finland, Tech. Rep. VTT.

[14] Samadi P, Mohsenian-Rad A H, Schober R, et al.Optimal Real-Time pricing algorithm based on utility maximization for smart grid[C]//Smart Grid Communications (SmartGridComm), 2010 First IEEE International Conference on, 2010: 415-420.

[15] Tarasak P. Optimal real-time pricing under load uncertainty based on utility maximization for smart grid[C]//Smart Grid Communications (SmartGridComm),2011 IEEE International Conference on, 2011: 321-326.

[16] Yang Jie, Zhang Guoshan, Ma Kai. Matching supply with demand: A power control and real time pricing approach[J]. International Journal of Electrical Power& Energy Systems, 2014, 61: 111-117.

[17] Asadi G, Gitizadeh M, Roosta A. Welfare maximization under real-time pricing in smart grid using PSO algorithm[C]//Electrical Engineering (ICEE), 2013 21st Iranian Conference on, 2013: 1-7.

[18] Weckx S, Driesen J, D'hulst R. Optimal real-time pricing for unbalanced distribution grids with network constraints[C]//Power and Energy Society General Meeting (PES), 2013 IEEE, 2013: 1-5.

[19] Ganesh A, Laevens K, Steinberg R. Congestion pricing and user adaptation[C]//INFOCOM 2001. Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings. IEEE, 2,2001: 959-965 vol.2.

[20] 韩水, 汪定伟, 张近朱. 利用边际成本法计算输电节点电价[J]. 东北电力技术, 2002, 23(3): 8-11.

[21] Chen L, Suzuki H, Wachi T, et al. Components of nodal prices for electric power systems[J]. Power Engineering Review, IEEE, 2001, 21(11): 54-54.

[22] 陈之栩. 节点边际电价与阻塞管理算法的研究[D].北京: 华北电力大学:北京, 2007.

[23] Herter K, Mcauliffe P, Rosenfeld A. An exploratory analysis of California residential customer response to critical peak pricing of electricity[J]. Energy, 2007,32(1): 25-34.

[24] Taylor T N, Schwarz P M, Cochell J E. 24/7 hourly response to electricity Real-Time pricing with up to eight summers of experience[J]. Journal of Regulatory Economics, 2005, 27(3): 235-262.

[25] Wolak F A. Residential customer response to real-time pricing: The anaheim critical peak pricing experiment[J].Center for the Study of Energy Markets, 2007.

[26] Meng Fanlin, Zeng Xiaojun, Qian Ma. Learning customer behaviour under Real-Time pricing in the smart grid[C]//Systems, Man, and Cybernetics (SMC),2013 IEEE International Conference on, 2013:3186-3191.

[27] Gottwalt S, Ketter W, Block C, et al. Demand side management—A simulation of household behavior under variable prices[J]. Energy Policy, 2011, 39(12):8163-8174.

[28] 张钦. 职能电网下需求响应热点问题探讨[J]. 中国电力, 2013, 46(6): 85-90.

[29] 熊雄, 杨仁刚, 叶林, 等. 电力需求侧大规模储能系统经济性评估[J]. 电工技术学报, 2013, 28(9):224-230.

[30] 孙近文, 万云飞, 郑培文, 等. 基于需求侧管理的电动汽车有序充放电策略[J]. 电工技术学报, 2014,29(8): 64-69.

[31] 张犁, 孙凯, 吴田进, 等. 基于光伏发电的直流微电网能量变换与管理[J]. 电工技术学报, 2013, 28(2):248-254.