建筑结构可靠度分析方法比较

文/冯惠苗 北京中外建建筑设计有限公司重庆分公司 重庆 400045

吕长浩 广东省华城建筑设计有限公司重庆分公司 重庆 400045

建筑结构可靠度分析方法比较

文/冯惠苗 北京中外建建筑设计有限公司重庆分公司 重庆 400045

吕长浩 广东省华城建筑设计有限公司重庆分公司 重庆 400045

详细阐述了结构可靠度计算方法，对一次二阶矩法中的中心点法、HL法、JC法、几何法，二次二阶矩法，响应面法，蒙特卡罗法，基于最优化原理的蒙特卡罗法的计算方法进行了分析；同时对四种常用的方法JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法，根据影响其结果精度的因素，以直接的蒙特卡罗法的结果为标准解，对其结果进行了对比分析。

结构可靠度；JC法；几何法；二次二阶矩法；基于最优化原理的蒙特卡罗法；功能函数

1 结构可靠度的计算方法

1.1 一次二阶矩法

一次二阶矩法计算简便，其要点是非正态随机变量的正态变换及非线性功能函数的线性化。

1.1.1 中心点法

设结构构件功能函数为）

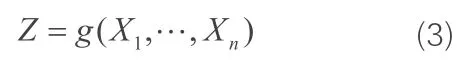
式中 Xi（ i = 1 ，2 ，… ，n ） 为统计独立正态随机变量。

将功能函数在 X i （i = 1 ，2 ，… ，n ） 的均值点 μXi（ i = 1 ，… ，n ） 展 T a y l o r 级数，仅保留线性项。有

Z的均值和方差

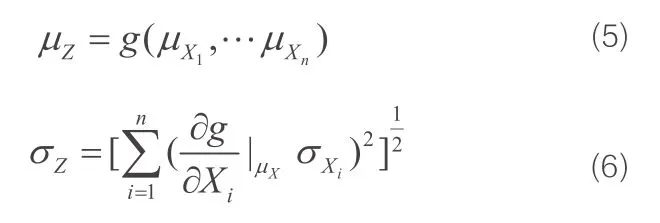
结构可靠指标

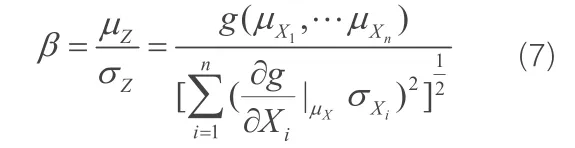
该方法对于非线性功能函数，因略去二阶及更高阶项，误差将随着线性化点到失效边界距离的增大而增大，而均值法中所选用的线性化点（均值点）一般在可靠区而不在失效边界上，误差较大[2］。

1.1.2 改进一次二阶矩法（HL法）

针对均值一次二阶矩法的上述问题，人们把线性化点选在失效边界上，且选在与结构最大可能失效概率对应的设计验算点上，以克服均值一次二阶矩法存在的问题，提出了改进的一次二阶矩法。该方法无疑优于均值一次二阶矩法，为工程实际可靠度计算中求解 β 的基础。

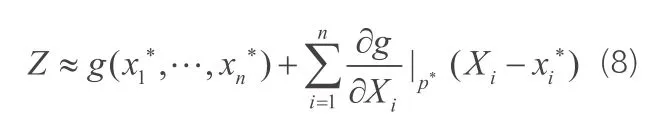
Z的均值和方差

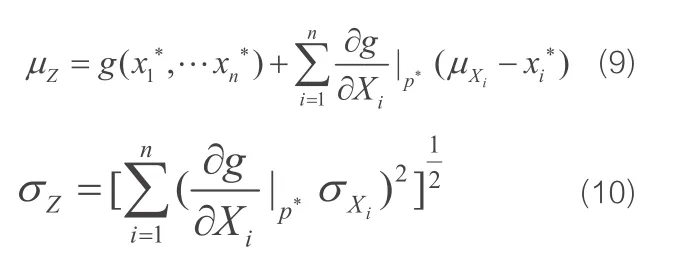
结构构件可靠指标可表示为

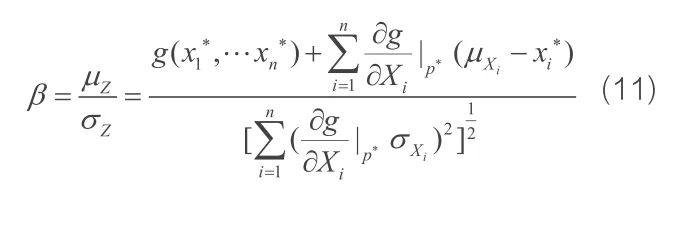
设计验算点坐标

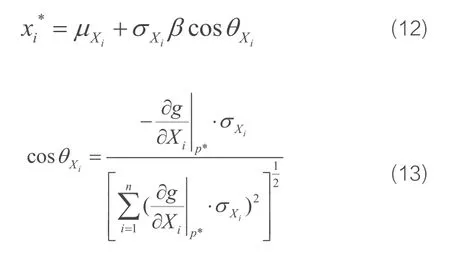
考虑到设计验算点 p*应位于极限状态曲面上，故，因此式（11）可写为

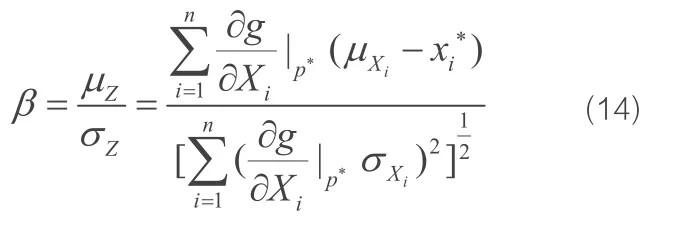
由于p*未知，不能直接利用上式求β。故β的求取只能采用迭代法。

但该方法只是在随机变量统计独立、正态分布和线性极限状态方程才是精确的，否则只能得到近似的结果[1］。

1.1.3 JC法

针对工程结构各随机变量的非正态性，拉克维茨提出了JC法。其基本原理是将非正态的变量当量正态化，替代的正态分布函数要求在设计验算点处的累积概率分布函数（CDF）和概率密度函数（PDF）值分别和原变量的CDF值、PDF值相等。当量正态化后，采用改进一次二阶矩法的计算原理求解结构可靠度指标。

（1）在验算点处，当量前后分布函数值相等；

（2）当量前后概率密度函数值相等。所以有：

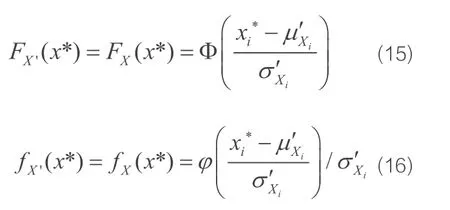
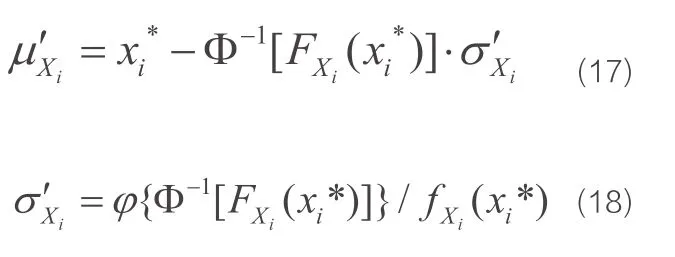
1.1.4 几何法

用以上方法计算时，迭代次数多，而且极限状态方程为高次非线性时误差较大，为此专家们提出几何法即是优化算法。根据可靠指标的几何意义，可靠指标的获得也就是在功能函数面上寻找一点y*，使该点与均值点的距离最短，从而使问题成为一个优化问题，即：目标函数：β = min （y*T · y*）1/2；约束条件：g（y*） = 0。用几何法求解可靠指标β的思路：先假设验算点x*，将验算点值代入极限状态方程g（x），若g（x*）≠0，则沿着g（x） = g（x*）所表示的空间曲面x*点处的梯度方向前进（后退），得到新的验算点x*代入极限状态方程，若g （x*） ＞ ε，其中ε为控制精度，继续迭代；若g（x*）≤ ε则表示该验算点已在失效边界上，迭代停止，即可求出β和x*的值。

设随机变量 X=（x1，x2，…，xn）T为相互独立的正态变量，通过变换得到一组相互独立的标准正态变量Y=（y1，y2，…，yn）T。

式中[T］，｛B｝分别为

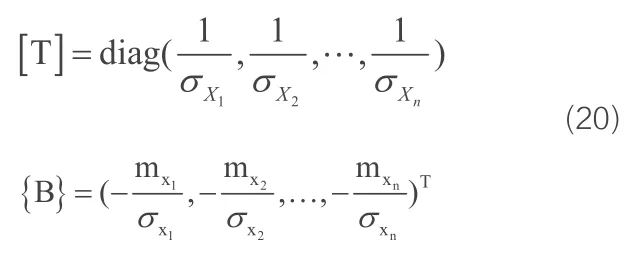
于是得到如下所示的结构功能函数

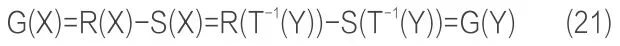
式中mxi为随机变量xi的均值，σxi为随机变量xi的标准差。

可用下面的迭代公式求得结构的可靠度指标β

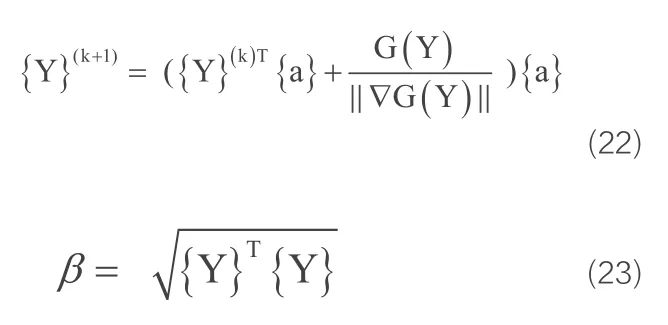
式中｛a｝和a分别为迭代点的移动方向及步长，即

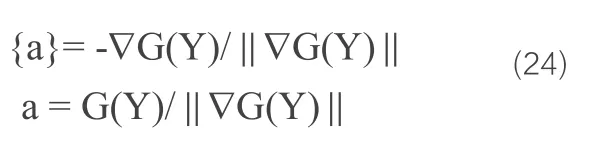
几何法与一般的一次二阶矩法相比，具有迭代次数少、收敛快、精度高的优点，但其结果亦为近似解。

1.2 二次二阶矩法

假设功能函数Z（X）= g（X）对于相关随机变量 X = （X1，X2，...，Xn）T的相关系数为 ρXi，Xj（i≠j），根据边际概率分布函数相等的原则，可以将其转换为标准正态随机变量 Y= （Y1，Y2，...，Yn）T，假设其相关系数矩阵为（25），显然，当X为正态随机变量时，ρYi，Yj= ρXi，Xj（i≠j），当X为非正态随机变量时，ρYi，Yj≈ ρXi，Xj（i≠j）。

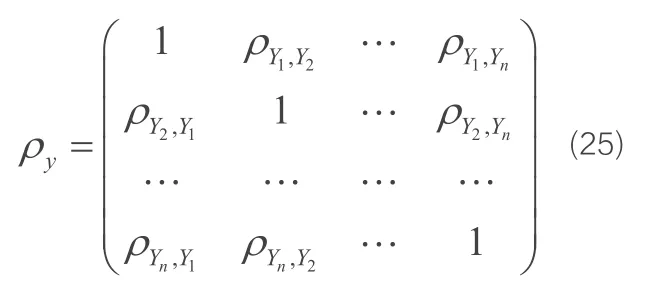
从而结构失效概率表达式为：

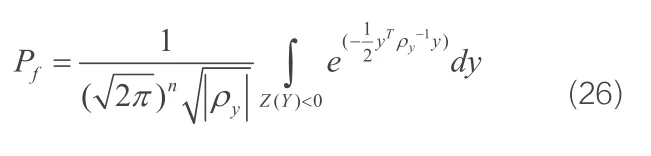
最终可以近似为：

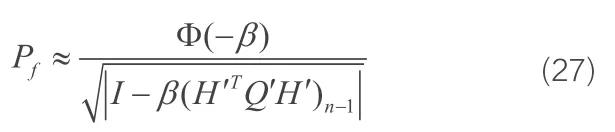
其中：

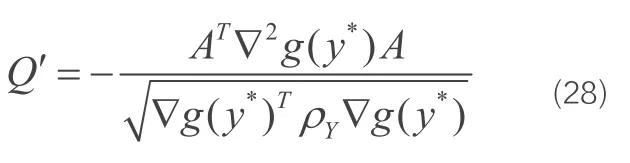
β为一阶矩可靠指标；y*为验算点；I 为单位矩阵；H′为正交变换矩阵，用于对随机变量Y′（=AY） 做正交变换：Y′=H′U；A 为相关系数矩阵ρY分解得到的下三角矩阵，即有ρY=AAT。

利用曲率κ （即 （H′TQ′H′）n-1的特征值矩阵），式（27）可以改写为：

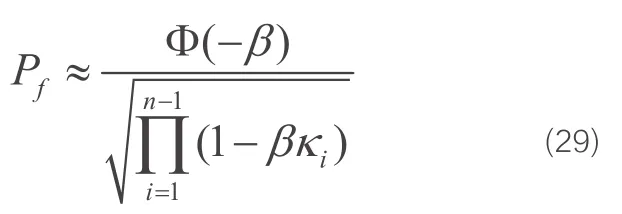
从公式的表达上可以看出，二次二阶矩法的结果是在一次二阶矩法结果的基础上乘一个考虑功能函数二次非线性影响的系数，所以可以看作是对一次二阶矩法结果的修正。需要强调的是，在广义随机空间中，对于随机变量变换前后相关系数的取值依据的是变换前后的相关系数近似相等，这相当于一次二阶矩法随机变量间的一次变换，对于二次二阶矩法是否考虑随机变量间的二次变换项，以及二次变换项如何考虑是需要进一步研究的问题。

1.3 响应面法

对于复杂结构而言，常难以写出功能函数的显式，而直接的数值模拟工作量太大，为此一些学者提出用响应面法确定结构功能函数。该方法的基本思想是采用有限次的数值试验，通过回归拟合解析表达式来代替真实功能函数曲面 Z= G（X1，X2，… ，XN），用二次多项式不含交叉项表示响应面函数的形式为

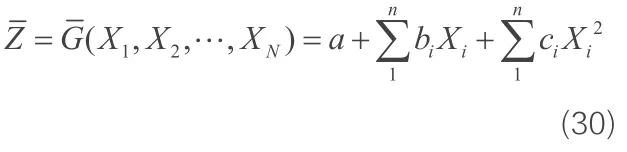
然后用插值方法来确定表达式中的未知参量，关键在于确定响应面函数的系数。多项式系数的确定一般以试验设计为基础，应用二水平因子设计或中心复合设计回归得到特定因子的最小二乘估计。响应面法用二次多项式代替大型复杂结构极限状态函数，并且通过系数的迭代调整，一般都能满足实际工程精度，具有较高的效率，很有使用价值，是一个很有发展前景的计算方法。

1.4 蒙特卡罗法

蒙特卡罗法又称随机抽样技巧、概率模拟方法和统计试验法。其理论基础是概率论中的大数定理，因此它的优点是其应用范围几乎没有什么限制。对基本变量相互独立的情况，设基本变量X1，X2，…，Xn的分布函数分别为Fx1（x1），Fx2（x2），…，Fxn（xn），令Fxi（xi） = rj，rj是由蒙特卡罗法产生的随机序列中的一个数。由此得到xi= F-1

xi（rj），i=1，2，…，n。对于每个 rj值可产生每个基本变量的相互独立的子样xi，将这些值带入失效函数g（x）得出一个取值。若g（x）≤0，则在计算机程序中记入一次失效函数的实现；若 g（x）＞0，则不记入，这样就完成了一次计算，再产生下一随机数，重复上面的计算，直至完成预定的试验次数为止。

此时，失效概率为

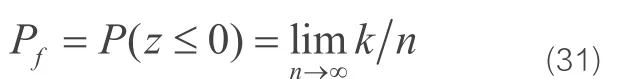
式中，n是试验的总次数，k是试验中g（x）≤0的次数，比值k/n是统计变量，对于低的失效概率或n较小时，估算Pf值容易发生相当大的不定性。但当模拟次数很大时，直至趋于无穷大时，能够得出精确的 Pf值；若基本随机变量相关时，利用条件概率密度，把多维问题化为一维问题来解决。

2 算例及各算法精度比较

2.1 函数非线性程度的影响

对于式（32）形式的功能函数，其非线性程度主要取决于系数k的大小，取k=1，2，3，4，5，6共六种工况进行分析。

假设X1为正态随机变量，X1的均值μx1=20，标准差σx1=4，对JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果进行比较，如下表所示。

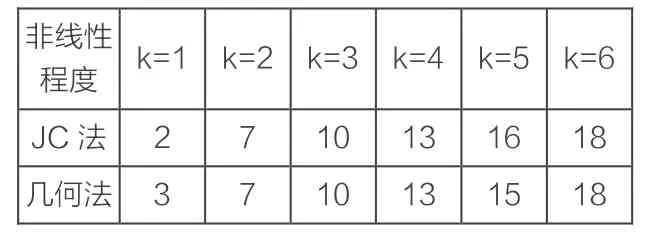
表1 HL法与几何法迭代次数比较

表2 不同非线性各算法精度比较

由表 1的数据可以看出，一次二阶矩法中的几何法在计算结构可靠指标时，其迭代次数与JC法相当。

由表2的数据可以看出，几何法的计算结果与JC法的计算结果相同；k=1时，即功能函数为线性时，JC法、几何法、二次二阶矩法、优化的 MC法的计算结果相同且都很接近于标准解；当功能函数为非线性函数时，二次二阶矩法的计算结果均大于一次二阶矩法的计算结果；当1＜k＜3时，此时功能函数非线性程度较小，几何法、JC法、二次二阶矩法、优化的MC法的计算结果有较小误差，仍接近标准解；k≥3时，随着功能函数非线性程度的增大，四种方法的计算结果的误差有所增大，优化的MC法误差最大；但k=5时，几何法、JC法、二次二阶矩法的结果接近于标准解。

2.2 函数变量类型的影响

对式（32）的功能函数，针对不同的变量类型，X1分别取对数正态随机变量、极值I型随机变量，取 k=1，X1的均值 μx1=20，标准差σx1=4，分别运用JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法计算结构可靠指标，并与上述正态随机变量情况下对比，如下表所示。

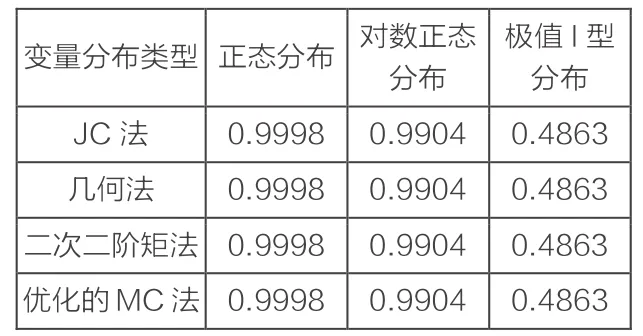
表3 不同变量类型各算法精度比较

由表3的数据可知，k=1时，此时功能函数为线性函数：当X1为正态随机变量和对数正态随机变量时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果接近于标准解，但正态随机变量的结果精度要优于对数正态随机变量的结果；当X1为极值I型随机变量时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的结果误差较大。

2.3 函数变量统计参数的影响

假设X1为正态随机变量，X1的均值μx1=20，取 k=1，2，X1标准差 σx1=4，5，6，7，8，9。以六种工况比较JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果，如下表所示。

表4 变量统计参数不同各算法精度比较（k=1）

表5 变量统计参数不同各算法精度比较（k=2）

由表4数据可知，k=1，功能函数为线性函数时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果相同，都很接近于标准解，且随着变量X1标准差的增大，精度变化不大。

由表5数据可知，k=2，功能函数为非线性函数时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果的精度随着变量X1标准差的增大而降低，且小于对应的表4的数据。

3 结论

通过以上对可靠度理论的常用的四种计算方法的研究，有如下结论：

（1）当功能函数为线性函数或非线性程度较低，变量为正态随机变量或对数正态随机变量，且变异系数较小时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果均可满足工程需要；

（2）当功能函数非线性程度较高，变量为极值I型随机变量，且变异系数较大时，JC法、几何法、二次二阶矩法、基于最优化原理的蒙特卡罗法的计算结果均有较大误差。

[1]李典庆，周建方.结构可靠度计算方法述评 [J］.河 海 大 学 常 州 分 校 学报，2000，14（1）：34-42.