基于不同方法计算椭球面上图斑面积的比较分析

□李铁 王建营

（1.天津市武清区规划建筑设计所，天津 武清 301700；2.天津市测绘院，天津 西青 300381）

基于不同方法计算椭球面上图斑面积的比较分析

□李铁1王建营2

（1.天津市武清区规划建筑设计所，天津 武清 301700；2.天津市测绘院，天津 西青 300381）

本文讨论在给定一个椭球面上不规则图斑的各个顶点的经纬度坐标的条件下，分别利用区域边界点高斯平面坐标和椭球面上梯形面积量算的精密公式两种算法来计算该区域面积，并且顾及测区离中央子午线的距离及投影面高程对面积量算的影响。并结合工程实例，对比分析了两种算法的优劣，可以为类似工程提供参考。

地球椭球面；不规则图斑；高斯投影；梯形算法

0.引言

面积测量是常见的测量工作，在土地规划、管理等工作中经常需要计算地类、宗地等各种类型的土地面积。目前，计算图斑面积通常做法是测出边界点的平面坐标，然后按平面上的封闭区域计算面积[1]。然而，一方面高斯投影会产生面积变形；另一方面地球表面也并非平面而是一个曲面，所以这样的算法计算出的结果必然与实际面积存在差异。本文通过对两种方法计算出的结果进行比较，讨论哪种算法更趋合理。

1.高斯投影计算椭球图斑面积

高斯投影计算椭球图斑面积实际上是将地面边界点从椭球面投影到高斯平面，再进行面积计算。这种方法带来的面积误差主要有三方面：一方面与测区距高斯投影中央子午线的距离有关；另一方面按照在高斯面上计算椭球图斑面积会产生差异；三是投影面高程也会对面积产生影响，但天津市绝大部分区域地势平坦本文不做讨论。

高斯投影长度变形m计算公式：

其中，η2=e2cos2B，l为大地经度与高斯投影中央子午线经度之差，B为大地纬度，单位均为弧度，e为椭圆第二偏心率。

面积变形即为长度变形的平方，在天津市若设纬度为39°，表1给出了测区离开中央子午线的距离与面积变形的关系：

表1 测区距离中央子午线的距离与面积变形的关系

2.椭球图斑面积梯形算法

图1

图2

由两条子午线和两条平行圈围成的椭球表面即为椭球面梯形，由图1可知，微分面积：

又因为：dx=MdB，dy=NdL，所以：

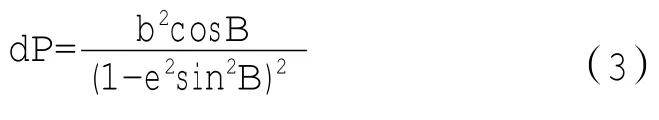
则通过积分得：

首先对经度积分得：

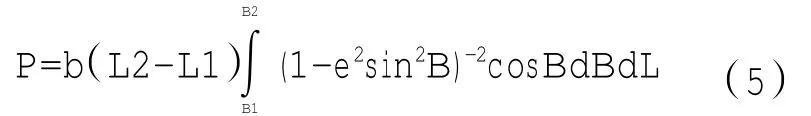
对纬度积分后得：

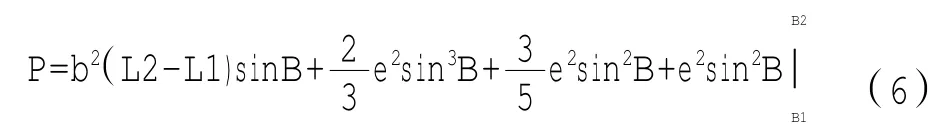
由于椭球图斑一般为不规则的多边形，如图2为一简单椭球面上多边形，点A、B在同一经线，点C、D在同一经线，点B、C在同一纬线，E为AD中点。由椭球面性质可知S1>S2，当微分量dL→0时，S1→S2，于是有椭球面多边形ABCD的面积等于椭球面梯形BCGF的面积。这样即可应用椭球面梯形面积公式对不规则椭球图斑的面积进行计算。

3.两种方法计算结果比较

在天津市不同区域选取宗地，应用这两种方法进行面积计算。其中平面面积计算采用天津市1990任意直角坐标，椭球面梯形计算采用WGS84大地坐标。比较结果如表2：

由表2可知，面积差值有正有负。这是因为高斯投影产生面积变形会使面积增大，而在高斯面上进行面积计算会使其变小。在宝坻的图斑，由于其距投影中央子午线较近投影面积变形影响较小，受到在高斯面上计算面积使其变小的影响，所以面积差值为负。其他几个区域由于其距投影中央子午线较远，主要受投影面积变形影响，所以为正。且距离中央子午线越远变形越大，如位于汉沽的图斑，距投影中央子午线最远，面积差值百分比也最大。

表2

另外，由表2看出位于大港和静海两个图斑前者面积小于后者，所处经度基本相同，但面积差值百分比差别较大，说明在高斯面上计算图斑面积随着图斑面积的增大而差异增加。

4.结束语

由以上的分析和实验结果可知，在高斯面上计算椭球图斑面积时，会受到多方面的影响而产生误差。高斯投影产生面积变形会使面积增大，且距投影中央子午线越远，影响越大；在高斯面上进行面积计算使椭球图斑面积变小，且随着图斑面积的增大而影响增加。而应用椭球面积梯形算法会避免这些情况，计算出的结果更趋合理。

【1】王解先，俞振武.高斯投影引起的面积计算误差[J].测绘通报,2003（4）:5-6.

【2】孔祥元，梅是义.控制测量学[M].武汉：武汉大学出版社，2005.

【3】钟宝琪等.地籍测量[M].武汉：武汉测绘科技大学出版社，1996.

【4】孔祥元，郭际明，刘宗全.大地测量学基础[M].武汉：武汉大学出版社，2001.

【5】谭福初，周世健，裴亚波.土地测量面积计算的几种方法[J].江西测绘,2008（2）:59-60.

【6】杨润书，向更明，张述清.高原地区不同坐标系及投影面引起的面积误差[J].测绘科学,2009（1）: 90-91.

【7】党亚民，成英燕,吴秀娟等.不同坐标系图斑理论面积计算研究[J].测绘科学,2005,30(6):23-24.

【8】朱益虎,席加伟,蒋毅等.图斑椭球面积计算方法研究[Z].江苏省测绘学会2009年学术年会论文集,2009:125-128.

【9】王文利,梁耘,陈俊英.任意封闭区域面积计算方法的研究[J].测绘技术装备,2008（1）:6-8.

P226+.2

A

2095-7319（2015）02-0018-04

李铁（1980—），男，大专，工程师，天津市武清区规划建筑设计所，现在主要从事工程测量方面工作。