中深孔爆破出矿巷道震动强度的数值模拟

邓飞， 韩晓亮， 廖声银， 王春晖， 胡龙飞， 尹丽冰

（1.江西理工大学资源与环境工程学院，江西 赣州 341000；2.浙江省高能爆破工程有限公司，杭州 310012；3.巴彦淖尔西部铜业有限公司，内蒙古 巴彦淖尔015000）

随着国民经济的复苏，矿业资源需求量的增长，矿山的开采规模也在不断扩大.当使用钻爆法进行矿石回采时，炸药爆炸所产生的能量，除少部分用于矿石的破碎外，大部分能量以地震波的形式在岩体介质中传播，引起邻近岩体的损伤，甚至造成岩体的局部承载能力下降，继而导致巷道片帮、冒顶等灾害的发生[1].同时，考虑到爆破施工的高频性及采场空间的密闭性，使得中深孔爆破作业下邻近出矿巷道表面质点震动强度预测的研究显得愈发紧迫.

目前，许多学者已经展开了对爆破动荷载作用下巷道表面质点震动强度的研究工作.夏梦会[2]通过MATLAB建立BP神经网络模型对浅孔爆破作业下巷道表面质点的震动强度进行预测，并将预测结果与传统公式的计算结果对比，发现BP神经网络具有较高的准确性.史秀志[3]通过ANSYS/LS-DYNA对中深孔爆破作业下阶段运输巷道的应力与震动强度进行分析，得到了巷道围岩的应力分布规律和质点震动强度随时间的变化规律.单仁亮[4]通过ANSYS/LS-DYNA对爆破掘进中巷道的动力响应进行分析，发现巷道质点的单元有效应力随时间的变化规律基本符合萨道夫斯基公式.虽然该领域已有众多研究成果，但均未对中深孔爆破作业下出矿巷道表面质点震动强度的预测进行研究.

随着采场内不断推进的回采作业，加之，作业空间的局限性，使得爆破震动对邻近出矿巷道的稳定性影响更加明显，故以此为现实依据，结合矿山生产实际，为维护出矿巷道的稳定，运用ANSYS/LS-DYNA对中深孔爆破作业下邻近出矿巷道表面质点的震动强度进行预测[5-6].

1 矿山概况

千家坪钒属于沉积层控型钒矿床，矿体主要位于下寒武统水沟口组含结核炭硅质岩、含结核泥质岩、黑色炭泥质岩中，岩层性质较稳定[7].矿体平均厚度20.70 m，矿体呈层状，形态简单，厚度变化较稳定.矿体产状较稳定，与围岩基本保持一致，倾向北[8].主要矿石为五氧化二钒，平均品位约1.05%，矿化较连续，品位分布均匀、稳定[9].

矿山目前采用水平扇形深孔阶段矿房法.采区中段高度均为50 m，矿房沿矿体走向布置，长约50 m，宽约为20 m，间柱长为6 m，顶柱为6 m；距矿体下盘边界约25 m处掘进阶段主运输平巷，并每隔8 m掘出矿进路；切割完成后，矿房底部会形成切割平巷，自切割平巷内每隔20 m掘切割天井，自人行通风天井每隔10 m掘分段联络道，并掘进分段凿岩硐室；矿石崩落后，使用内燃铲运机铲出，通过矿用三轮车运至溜井并卸矿到最下部中段，统一由电机车运送至选厂处理[10-12].

2 爆破振动测试

矿山钻孔采用水平中深孔，起爆采用非电导爆系统，爆破采用2#岩石乳化炸药，炮孔孔径76 mm，炮孔排距a=1 500～2 000 mm，炮孔底距b=2 000～2 500 mm，扇形布置炮孔，共布置80个炮孔，分5段起爆，每段装药量为 160 kg（1 段），180 kg（3 段），160 kg（5 段），260 kg（7 段），230 kg（9 段），总装药量 990 kg.爆破作业地点995 m中段2号采场，测试地点1 045 m中段2号采场1号、2号、3号进路底板，垂直方向爆心距约为32 m，水平方向爆心距分别为28.2 m、36.7 m、45.2 m，3个测点在出矿巷道处，每处布置1台测振仪，测点如图1所示，测试结果如表1所示.

3 LS-DYNA爆破震动的数值模拟

19世纪80年代，J.O.Hallquist博士在Lawrence Livermore National Laboratory实验室完成对LSDYNA研发工作，由于其采用中心差分格式进行积分，且算法以 Lagrange为主，兼有ALE和 Euler，故使得其得到岩土工程各界的广泛应用.

表1 各测点实测振速值Table 1 Peak vibration velocity of text on monitoring points

3.1 数值计算模型的建立

结合千家坪钒矿实际生产，运用ANSYS/LSDYNA建立数值计算模型对中深孔爆破作业下出矿巷道的震动强度进行预测.考虑到模型求解的可行性，本次数值计算仅对995 m中段2号采场中深孔回采爆破作用下1 045 m中段2号采场1号、2号、3号出矿巷道的震动强度进行分析.为最大程度地降低数值计算工作量，并尽可能地保证数值计算结果的准确性，故对数值计算模型做以下处理.

1）忽略地表自重应力影响；

2）建立1/2实体模型；

3）将同一段别起爆的炸药折算为集中药包，并将其均匀布置在采场内；

4）将矿山实际出矿巷道近似为长方体；

5）为降低数值计算工作量模型采用m-kg-s单位制，考虑到炸药量大小，故将炸药附近的网格进行细化.

结合矿山生产实际，模型尺寸（长×宽×高）为30 m×50 m×50 m；巷道距离左侧边界3 m，巷道距离右侧边界2 m，巷道间距8 m，巷道尺寸（长×宽×高）为3 m×25 m×4 m；炸药底部留3 m岩层；3 m岩层至模型底部边界布置2 m空气；炸药布置于模型右侧边界右下角位置；区域具体布置如图2所示，炸药具体布置如图3所示.

3.2 空间有限元离散化

ANSYS/LS-DYNA为更切实际的描述模型材料的物理力学性质，提供了丰富的单元库，且这些单元均是采用线性位移插值函数的低阶单元，可以很好地运用于各种大变形以及材料失效等高度非线性问题的分析中.结合工程实际，本次数值计算岩石、炸药、空气材料均采用由8个节点构成的三维显示结构实体单元SOLID164[13-16].

3.3 岩体物理力学属性及模型

ANSYS/LS-DYNA为更真实的描述自然界岩石介质提供了线性、非线性、离散单元、刚体及状态方程相关等5种材料模型供用户选择使用，结合工程实际，本次数值计算采用弹塑性材料模型定义泥页岩，其主要物理力学参数见表2.

图2 有限元模型图Fig.2 Model diagram of finite element

图3 炮孔附近加密图Fig.3 Mesh refinement near blast hole

表2 泥页岩物理力学参数表Table 2 Parameter shale of physical and mechanical

3.4 炸药材料模型及状态方程

炸药选用 2#岩石乳化炸药，采用MAT_HIGH_EXPLOSIVE_BURN模型，主要参数见表3，采用JWL方程描述炸药状态.

表3 炸药参数表Table 3 Parameter shale of explosive

3.5 空气材料模型及状态方程

空气采用NULL材料模型以及LINEAR_POLYNOMIAL状态方程加以描述，主要参数见表4.

表4 空气参数表Table 4 Parameter shale of air

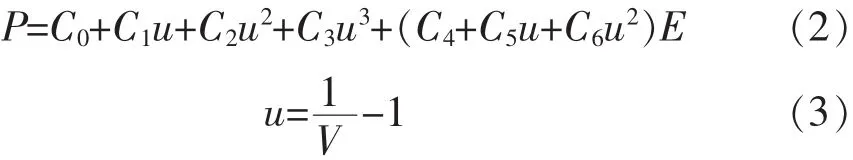
3.6 边界处理

LS-DYNA为更清晰的描述现场地质条件提供了零位移边界、循环对称边界、无反射边界3种边界条件供用户选择使用.结合工程实际，模型右侧（炸药侧）选择循环对称边界；模型顶部选择自由边界，模型其他位置选择无反射边界.

3.7 算法选择

ANSYS/LS-DYNA为更方便的处理连续体提供了Lagrange、Euler及ALE 3种算法供用户选择使用.Lagrange算法主要用于固体结构的应力应变分析，可以准确的描述边界结构的运动；Eule算法主要用于流体分析，其各个迭代过程数值计算的精度是相同的；ALE算法主要用于大变形问题的分析，可以根据要求在运算中适当调整网格的位置；结合工程实际，本次数值计算中，岩石、空气选用Lagrange算法，炸药选用ALE算法.

3.8 ANSYS/LS-DYNA数值计算结果分析

通过坐标系在模型中按照实测距离中布置3个测点，具体位置见图4（其中单元53 376、单元53 364、单元53 352分别代表图5中的b、c、d）；对模型表面各监测点爆破后3 s内的振动速度进行监测，并绘制0.4 s内速度-时间曲线，如图 5（a）～图 5（d），振速见表 5.

图4 数值计算中测点布置Fig.4 Location map about numerical simulation monitoring point

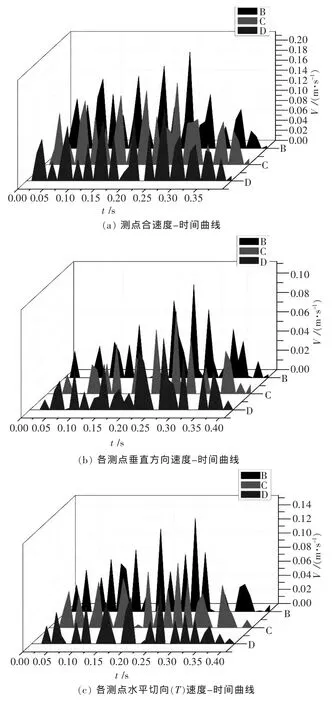
图5 各测点振动速度-时间曲线Fig.5 Velocity curves of explosives blasting

表5 点模拟计算振速峰值Table 5 Peak vibration velocity of numerical simulation on monitoring points

通过对图5分析可知，1号测点的峰值振动速度最大，且3个测点的峰值振动速度随着爆心距的增加逐渐降低；各测点各方向的振动速度均在0.25 s前后达到了峰值；各测点各方向的震动速度随着各段的炸药量的依次起爆，逐步增加直至达到峰值，且达到峰值振速前，出现的波峰数量与炸药的段数一致；各测点各方向振动速度随时间（加速度）的变化幅度与单段炸药装药量的变化幅度成线性关系，且单段起爆炸药量变化愈大，各测点各方向振动速度随时间（加速度）的变化愈明显；本次爆破震动持续时间长达400 ms左右.

通过对比分析表1与表5可知，数值计算所得各测点各方向振动速度均比实际测量所得的振动速度值略大.

出矿巷道属于矿山隧道，主震频率为30～80 Hz，根据根据我国GB6722-2003《爆破安全规程》可知，矿山隧道所允许的峰值振速为15～30 cm/s.1号、2号测点的实测与数值计算的震动数据均达到此最低阀值，结合爆后现场观测，1号、2号测点所处的出矿巷道已经出现了片帮、冒顶等险情；3号测点的实测与数值计算的震动数据均没有达到此阀值，结合爆后现场观测，3号测点所处的出矿巷道也出现了小范围的裂缝.考虑到矿体由下至上的逐层开采的生产因素，出矿巷道受到回采爆破的影响会愈发明显.建议千家坪钒矿在今后的生产过程中对采场的爆破参数进行优化，减少爆破震动对矿山隧道的影响；对受爆破震动影响较为明显的区域要采取多种支护方式进行联合支护，并结合雷达探伤技术做好对矿山隧道失稳工作的预测.

4 结 论

通过对数值计算结果与实测数据的分析发现，本次爆破作业参数可供995 m中段采场的中深孔爆破施工作业借鉴，但随着爆破作业的深入，为维护出矿巷道的稳定，应适当地加强巷道的支护措施，并结合雷达探伤做好对巷道失稳的预测工作.

通过对数值计算结果与实测数据的对比发现，LS-DYNA数值计算结果较现场实测数据略大，其主要原因是将同段起爆的多孔药包按照集中药包进行处理，使炸药爆炸时产生的能量更加集中，继而导致爆破震动强度的增加；矿层存在一定数量的裂隙，可起到一定的减震作用，同时，裂隙中富含少量的水分，可在一定程度上加强爆破震动强度，而数值计算中均当做匀质矿体进行处理；总体上讲，运用LS-DYNA对爆破震动强度的预测具有一定的指导价值.

[1]郭建国.急斜特厚煤层综放回采巷道稳定性控制研究[D].西安：西安科技大学,2010.

[2]夏梦会,董香山,张力民,等.神经网络模型在爆破震动强度预测中的应用研究[J].有色金属(矿山部分),2004,56(3):25-27.

[3]史秀志,陈寿如.爆破振动信号时频特征的微差时间效应[J].湖南科技大学学报(自然科学版),2008,23(3):10-13.

[4]单仁亮,王二成,宋立伟,等.直墙半圆拱巷道爆破震动数值分析[J].岩土力学,2013,34(增刊1):437-443.

[5]管然发.锚网带支护在巷道修复中的应用[J].煤炭技术,2003,22(8):54-55.

[6]王春生,杨忠.浅谈缓倾斜突出煤层石门揭煤时的放炮方式[J].煤炭技术,2003,22(8):55-56.

[7]刘晓军.千家坪钒矿薄层状矿体开采爆破参数优化研究[D].赣州：江西理工大学,2012.

[8]朱明.千家坪钒矿急倾斜厚大矿体采矿方法优化研究[D].赣州：江西理工大学,2012.

[9]冯勇.千家坪钒矿采场稳定性分析[D].赣州：江西理工大学,2011.

[10]张永生.土体稳定性弹塑性大变形有限元分析[D].哈尔滨：哈尔滨工程大学,2005.

[11]袁泉.开合屋盖结构碰撞响应及减振分析[D].天津：天津大学,2007.

[12]黄勇.民用飞机水上迫降数值模拟计算研究[C]//第十届全国振动理论及应用学术会议论文集,南京：中国振动工程学会，2011:1130-1137.

[13]朱俊,杨建华,卢文波,等.地应力影响下隧洞边墙的爆破振动安全[J].爆炸与冲击,2014,34(2):153-160.

[14]姚强,杨兴国,陈兴泽,等.大型地下厂房开挖爆破振动动力响应数值模拟[J].振动与冲击,2014(6):66-70.

[15]张智超,陈育民,刘汉龙,等.微差爆破模拟天然地震的数值分析与效果评价[J].岩土力学,2013,34(1):265-274.

[16]夏祥,李海波,李俊如,等.岩体爆生裂纹的数值模拟[J].岩土力学,2006,27(11):1987-1991.