密山地电场数据小波包去噪研究
梁 跃董桂菊崔天时张东海
1)中国哈尔滨 150030 东北农业大学
2)中国黑龙江 157009 黑龙江省牡丹江地震台
3)中国黑龙江 158300 黑龙江省密山地震台
密山地电场数据小波包去噪研究
梁 跃1),2)董桂菊1)崔天时1)张东海3)
1)中国哈尔滨 150030 东北农业大学
2)中国黑龙江 157009 黑龙江省牡丹江地震台
3)中国黑龙江 158300 黑龙江省密山地震台
选取2009年11月21日密山市知一镇地震发生当天密山地电场数据,采用小波包阈值去噪算法,对地电场数据进行去噪研究,还原地震发生后地电场数据变化信息,并结合去噪效果及误差分析结果,选出适合密山地电场数据去噪的最优小波函数。
地电场;小波包;小波;阈值去噪;小波函数
0 引言
小波变换自出现以来因其优越的时频分析特性,已经广泛应用在信号分析、图像处理、地震勘探数据处理等诸多领域。小波包变换是由小波变换进一步发展而来的,同小波变换相比,小波包变换具有更高的时频分辨率及更加优越的去噪性能,尤其对于非平稳信号,小波包去噪已经成为信号处理的主流方向之一。魏红梅等(2008)将小波包去噪方法应用于地震信号的预处理中,削弱了地震信号中的高、低频干扰信号。邱颖等(2009)应用小波域阈值滤波方法对叠加在大地电场信号上的地电阻率人工供电干扰信号进行滤波处理。王培茂等(2011)提出基于匹配算法的小波包去噪方法,很好地压制了地震信号中的白噪声。
地电观测资料信息量大,各种高频信息丰富、干扰因素复杂(张彩艳等,2011)。密山地电场观测数据一直存在类似尖脉冲干扰信号,可能是由多种不同因素叠加到一起造成的(高研等,2012)。2009年11月21日密山市知一镇发生ML3.7地震,密山地震台测定震中距为27.8 km,地震发生前后密山地电场数据均未体现任何变化信息。本文以此次地震为例,采用小波包阈值去噪方法,还原地震发生后地电场数据中的变化信息,并选出适合密山地电场数据去噪的小波函数。
1 原理及方法
自1822年傅里叶变换发表以来,傅里叶变换一直是信号处理领域中应用广泛的分析手段。但是,由于傅里叶变换是一种全局变换,无法表述信号的时频局部特性。尽管窗口傅里叶变换的提出实现了信号在时频域内局部化的联合分析,但因其时频窗的宽度是固定不变的,无法根据信号的频率变化进行调整。小波变换继承和发展了窗口傅里叶变换的局部化思想,克服了窗口大小不随频率变化的缺点,在低频部分具有较低的时间分辨率和较高的频率分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,是一种比较理想的信号处理工具。小波包变换是基于小波变换的进一步发展,其优一点在于,小波包分解对小波分解中没有细分的高频部分做进一步分解,具有更高的时频分辨率,图1和图2分别为小波及小波包的3层分解结构图。

图1 小波3层分解结构Fig.1 Three layer structure chart of wavelet decomposition
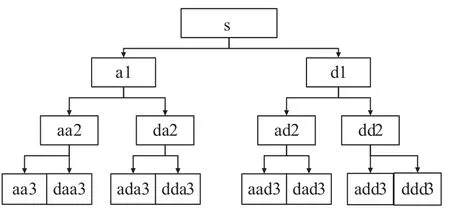
图2 小波包3层分解结构Fig.2 Three layer structure chart of wavelet packet decomposition
1.1 小波包变换定义
在多分辨率分析中,定义尺度函数空间Vj和小波函数空间Wj,尺度函数φ(t)和小波函数ψ(t)存在以下二尺度方程


将式(1)和式(2)推广为


小波包变换的重构算法为

1.2 阈值去噪法
阈值去噪法认为,与有用信号对应的小波包系数包含重要信息,所以其幅值大、数目少;而与噪声对应的小波包系数幅值小、数目多。通过选取适当的阈值,对各尺度上的小波包系数进行阈值处理,去掉与噪声对应的系数信息,从而达到信号去噪的目的。
小波包阈值去噪的步骤如下:①选择小波函数并确定分解层数N,然后对数据进行N层小波包分解;②提取阈值,并对小波包系数进行阈值处理;③小波包重构,重构后得到去噪信号。在小波包去噪的过程中,核心的环节是在系数上作用阈值的过程,阈值选取的得当与否直接影响去噪的质量。
2 数据选取及去噪参数确定
2.1 地电场数据选取
北京时间2009年11月21日06时47分密山市知一镇(131.81°E,45.53°N)发生ML3.7地震,密山地震台测定震中距为27.8 km。选取密山地电场2009年11月21日00∶00至09∶59(北京时)东西(EW)向长极距和NS向长极距分钟值数据进行小波包去噪处理。
2.2 小波函数选择及分解层数确定
小波函数具有紧支性、对称性、正则性和消失矩阶数等性质。紧支性保证小波函数具有优良的空间局部特性,函数的支撑宽度越小,局部化能力越强;对称性又称为线性相位特性,保证函数的滤波特性具有线性相移,不会造成滤波后信号的失真;正则性用来刻画函数的光滑程度;消失矩阶数反映了变换后能量的集中程度,消失矩阶数越大正则性越好。几种常用小波函数参数特性对比见表1。
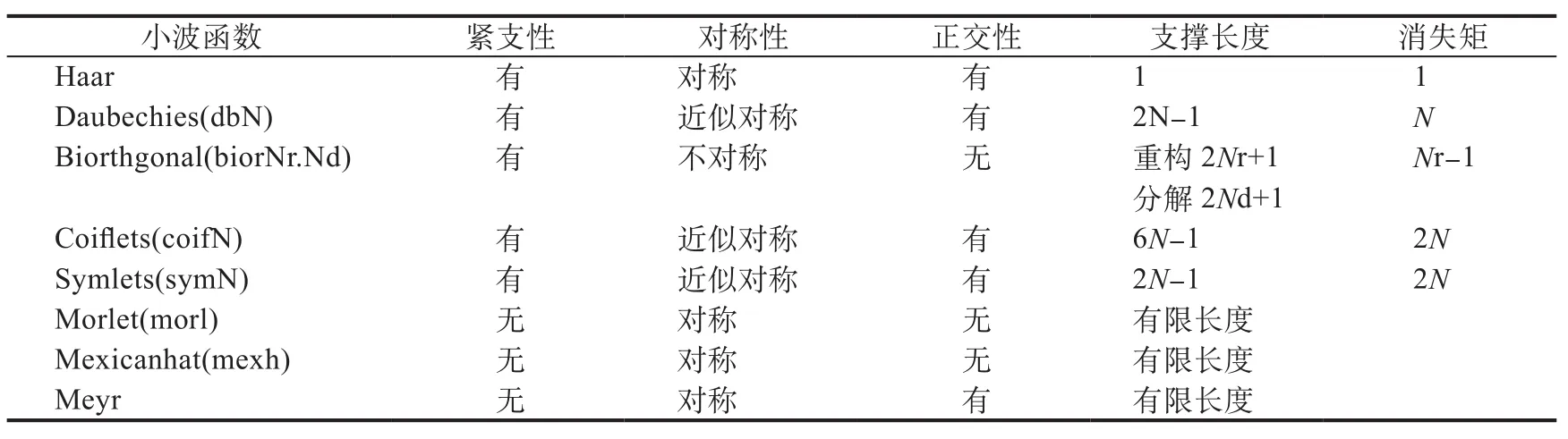
表1 小波函数参数特性比较Table 1 Parameter characteristics of different wavelet functions
由于密山地电场数据中高频干扰较多,所以选择的小波函数必须具备良好的紧支性,以保证良好的局部性能;为了有利于分解后信号的精确重构,小波函数应具有较好的正交性;应具备较好的对称性及较高的消失矩阶数。对比表1 中各小波函数的参数特性,Daubechies(dbN)函数符合本次研究对小波函数特性的要求。
因为小波函数的各种特性不可能同时达到最优,例如,函数的消失矩阶数越大,正则性越好,函数越光滑;但函数的支撑长度随之变大,紧支性降低。在dbN系列函数中,“N”代表消失矩阶数,其支撑长度为“2N-1”。考虑到消失矩阶数与支撑长度之间的平衡,N不能太大也不能太小。因此,选择Daubechies(dbN)系列中的 “db3”、“db4”、“db5”、“db6”函数进行密山地电场数据的去噪处理,并根据去噪结果选出最佳小波函数。
正常地电场信号的能量分布在0—0.005 Hz,所以对含有干扰的地电场信号的分解层数可选择6层或7层分解(邱影,2008),本次研究选择7层小波包分解。
3 数据处理分析
首先采用ddencmp阈值获取函数获取EW向地电场数据在小波包去噪过程中的默认阈值,然后使用“db3”、“db4”、“db5”及“db6”函数对数据进行小波包阈值去噪处理,去噪方式为硬阈值去噪,熵标准默认为sure熵标准,去噪结果见图3,图中箭头所指时间为地震的发震时刻(下同)。

图3 EW向数据小波包阈值去噪(a)EW向数据;(b)db3去噪;(c)db4去噪;(d)db5去噪;(e)db6去噪Fig.3 wavelet packet threshold de-noising on EW
与地震有关的自然电场异常是因为在孕震体及其周围,受统一应力场变化的影响,地下流体的冲流、过滤、定向作用使自然电场出现异常(马钦忠等,2004),而自然电场的异常必然造成该区域内大地电场发生变化。如图3(a)所示,由于地电场数据干扰较多,EW向数据中未显示任何震后变化信息。将图3中各个函数的去噪结果进行比较,随着函数消失矩阶数的增大,去噪后的信号越来越光滑,但函数的局部性能逐渐下降,去噪后细节信号丢失越严重。db3函数消失矩阶数最小,去噪后信号不光滑,存在失真现象;db6函数消失矩阶数最大,去噪后信号最光滑,但因局部性能较差,去噪后原始信号中的细节信息丢失较严重,未能还原地震发生后的任何变化信息。如图3(c)所示,db4函数在去除大部分高频干扰的同时,还原地震发生后地电场信号中的变化信息。由于地下流体的冲流、过滤等物理化学变化需要一定时间,所以地电场的同震变化信息略滞后且持续一段时间,图3(c)中地震发生后地电场的波动变化持续近半小时。
计算去噪后信号与原始信号之间的均方根误差(RMSE)及相对误差(error)值,见表2。
均方根误差的定义为,原始信号与小波包去噪后重构信号之差平方期望值的平方根;相对误差的定义为原始信号与去噪后信号之间的差异。由表2可见,EW向数据,db4函数小波包去噪信号的两项误差值均小于其他函数,且图3中db4函数的去噪效果最优。所以,密山地电场EW向数据的最佳小波函数为db4函数。
同理,得出密山地电场NS向数据的最佳小波函数为db5函数,NS向数据小波包去噪信号的均方根误差(RMSE)和相对误差(error)值见表2。

表2 EW向数据误差分析和NS向数据误差分析Table 2 Error analysis of EW data
如表2所示,NS向数据db5函数小波包去噪信号的均方根误差(RMSE)和相对误差(error)值略大于db3函数,但小于db4和db6函数;此外,因db5函数的正则性和消失矩阶数均优于db3函数,所以,密山地电场NS数据的最佳小波函数为db5函数。
4 结论
通过对2009年11月21日密山地电场数据的小波包去噪结果进行分析,得出以下结论。
(1)密山地电场数据确实存在大量干扰噪声,通过小波包去噪方法去除大部分高频干扰,还原地震发生后地电场数据的变化信息。
(2)综合分析,密山地电场EW向数据去噪的最优小波函数为db4函数,NS向数据去噪的最优小波函数为db5函数。
(3)除地震发生时刻及其后一段时间以外,其他时刻的地电场数据仍存在类似突跳的干扰信息,需今后进一步研究。
边威.小波基的选取与构造方法讨论[D].长春:东北师范大学,2007.
陈强,黄声享,王韦.小波去噪效果评价的另一指标[J].测绘信息与工程,2008,33(5):13-14.
高研,张亚江,李明忠,等.密山地震台地电场干扰分析研究[J].地震地磁观测与研究,2012,33(1):70-74.
马钦忠,冯志生,宋治平,等.崇明与南京台震前地电场变化异常分析[J].地震学报,2004,26(3):304-312.
邱影.地电场观测中已知源干扰抑制研究[D].北京:中国地震局地震预测研究所,2008.
邱颖,席继楼.小波方法在地电场干扰处理中的分析研究[J].地震,2009,29(2):57-63.
陶珂,朱建军.小波去噪质量评价方法的对比研究[J].大地测量与地球动力学,2012,33(2):128-133.
唐晓初.小波分析及其应用[M].重庆大学出版社,2006:96-98.
魏红梅,黄世源,许飞.小波包去噪在地震信号预处理中的应用[J].东北地震研究,2008,24(2):45-49.
王培茂,杨冬红,高茹,等.基于匹配小波包算法的地震信号去噪[J].世界地质,2011,30(2):277-281.
席继楼,赵家骝,王燕琼.大地电场测量系统中的特殊抗干扰技术[J].电子技术应用,1999,125(12):30-32.
张彩艳,赵洁,雷功明,等.甘肃嘉峪关地震台大地电场观测数据干扰分析[J].山西地震,2011,4:25-28.
张德丰.Matlab小波分析[M].北京:机械工业出版社,2010:158-196.
Research of wavelet packet de-noising on Mishan geoelectric fi eld data
Liang Yue1),2),Dong Guiju1),Cui Tianshi1)and Zhang Donghai3)
1) Northeast Agricultural University,Harbin 150030,China
2) Mudanjiang Seismic Station,Heilongjiang Province 157009,China
3) Mishan Seismic Station,Heilongjiang Province 158300,China
This paper,based on the data of the earthquake that took place in the Zhiyi town of Mishan on 21 November,2009 and was collected by the Mishan Seismic Station geoelectric fi eld(hereinafter referred to as Mishan geoelectric field),makes de-noising research of geoelectric field data by using wavelet packet threshold de-noising algorithm,and restores the change information in geoelectric fi eld data after the earthquake.In addition,it screens out the optimal wavelet functions which are appropriate for the Mishan geoelectric fi eld data de-noising according to the de-noising effect and the error analysis results.
geoelectric fi eld,wavelet packet,wavelet,threshold de-noising
10.3969/j.issn.1003-3246.2015.01.014
梁跃(1988—),男,黑龙江五常人,硕士,主要从事地震监测工作,E-mail: 381665839@qq.com
中国地震局2014年度“地震监测、预测、科研三结合”课题(140801)资助
本文收到日期:2014-09-29

