时间谐波对永磁同步电机损耗的影响规律

佟文明 朱晓锋 贾建国 段庆亮

（沈阳工业大学国家稀土永磁电机工程技术研究中心 沈阳 110870）

1 引言

近年来，随着电力电子技术的发展，变频器在电机领域得到了广泛的运用[1]，使得电机能够在很宽的频率范围内工作。然而，变频器供电时引入了大量电流时间谐波，这些谐波会影响电机内部磁场[2]，使得永磁电机附加损耗大大增加。一方面，这将使电机效率降低，尤其对于超高效电机，影响更甚；另一方面，由于转子散热困难，其在永磁体内产生的涡流损耗会引起永磁体局部温升过高，甚至发生局部不可逆失磁，从而影响电机的使用寿命和可靠性[3,4]。因此，准确计算损耗大小并研究其分布规律具有积极意义。

变频器供电时由于电流时间谐波引起的损耗称为附加损耗，包含四部分：①绕组中的附加损耗。高次时间谐波电流通过绕组时，使其横截面上的电流密度向外表面分布，等效电阻变大，产生趋肤效应，由此产生的损耗增量称为绕组附加损耗；②附加铁耗。由于时间谐波电流产生的磁场在定、转子铁心中交变而引起的铁耗增量即附加铁耗；③永磁体涡流损耗。时间谐波电流产生的磁场与转子转速不保持同步，使得谐波磁场在永磁体中交变，进而产生涡流损耗；④周围结构件涡流损耗。时间谐波电流产生的磁场会在周围金属结构件中交变，引起涡流损耗。

国内外已有许多人对变频器供电时电机损耗进行了研究，并取得了一定的成果。文献[5]运用二维场路耦合时步有限元法，研究了调制比和载波比对永磁同步发电机定子损耗的影响；文献[6]推导了PWM 逆变器供电下电机铁心损耗的解析算法，从解析公式的角度给出了调制比与铁耗的关系，认为调制比越大，铁耗越小；文献[7]研究了变频器参数与谐波铁耗的关系，对变频器供电时的铁耗公式进行了修正；文献[8]研究了基波以及谐波铁耗在异步电机定转子铁心中的分布特点，分析了空载运行时铁心不同位置磁通密度随时间变化波形，并得出铁心不同区域的铁耗分布情况；文献[9]研究了变频器开关频率对电机铁耗的影响，认为电机铁耗随开关频率增大而减小，但由于开关频率增大到一定程度时电流谐波减少趋势变缓，因此铁耗变化最后趋也于平缓；文献[10]认为变频器供电时产生永磁体涡流损耗的源是齿谐波与时间谐波，而且时间谐波占主要因素；文献[11]对电机磁动势进行了谐波分析，并运用二维有限元法，计算了电机定、转子铁心涡流损耗和永磁体内涡流损耗。文献[12,13]分析了转子涡流损耗产生的根源，并运用有限元法对这部分损耗进行了计算。

上述文献在计算和分析变频器供电损耗时，重点针对总损耗数值进行计算和研究。

本文以一台4.2kW、8极表面式永磁电机为例，采用时步有限元法，计算分析了空载变频器供电时电机定子铁心不同位置的磁通密度随时间变化，得到定子铁心不同区域的附加损耗分布情况；通过对永磁体径向等分，得到永磁体涡流损耗的分布规律；通过分析不同调制比（a，定义为变频器输出线电压幅值比上直流母线电压）、开关频率fc、气隙长度δ和转子磁路结构时电机不同部位的磁通密度，研究电机各部位附加损耗随这些参数的变化关系；搭建了一套正弦波供电和变频器供电实验平台（附加损耗为变频器供电与正弦波供电空载铁耗之差），通过同时对4.2kW、6.9kW和9.42kW电机（结构相似，都为8极36槽、不等气隙表面凸出式）的实验结果分析，验证了附加损耗随变频器参数的变化规律。文中研究成果为降低变频器供电电机损耗提供重要支持。

2 损耗计算模型和电机参数

2.1 定子绕组h次时间谐波电流产生的气隙磁通密度

为了研究永磁同步电动机中的损耗，必须知道它产生的机理、分布情况，从而采取相应的措施以降低其对永磁同步电动机性能的影响。下文将从气隙磁场的角度出发，首先分析时间谐波电流产生的磁场分布，进而研究电机损耗分布。

取A相绕组的轴线为空间角度θ的坐标原点，并选择 A相电流达到最大值的瞬间作为时间的零点，不考虑不同次数谐波电流初相位的影响，三相绕组电流可表示为[14]

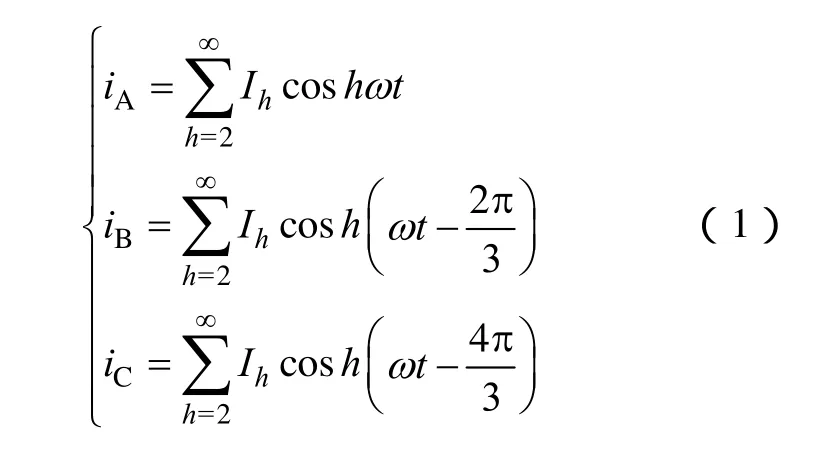
式中h——时间谐波次数，其为大于1的正整数；

Ih——h次时间谐波所对应的电流幅值；

ω——基波电流的电角频率。

于是A、B、C三相绕组绕组中的h次时间谐波电流所产生的ν次空间脉振磁动势表达式为

式中Fφ——相磁动势谐波幅值。

于是，h次时间谐波电流所产生的v次空间谐波合成磁动势为

通过对式（3）的分析，可得出以下结论：

忽略定子谐波磁动势作用于谐波比磁导所产生的空间谐波磁场，则时间谐波电流引起的气隙磁场表达式为[15]

式中λ(θ)——气隙比磁导；

Λ0——气隙磁导的恒定分量。

2.2 基于时步有限元的铁耗计算模型

由上节分析可知，h次时间谐波电流产生的磁场相对于定、转子运动，磁通密度在铁心中不断交变，进而产生大量的损耗。本文采用二维有限元法计算了定、转子铁心中由于电流时间谐波引起的铁耗，其可以认为是径向磁通密度Br和切向磁通密度Bt共同作用的结果，具体为[14]

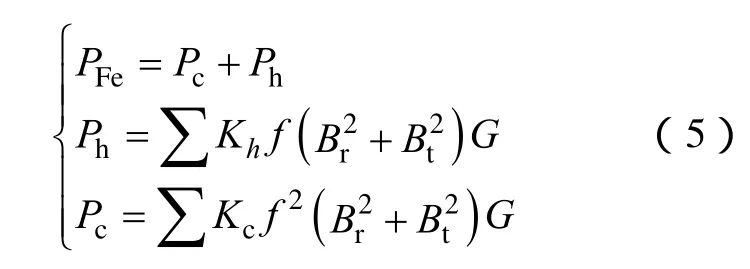
式中Ph，Pc——磁滞、涡流损耗；

Kh，Kc——磁滞、涡流损耗系数；

f——磁通密度频率；

Br，Bt——磁通密度的径向和切向分量；

G——铁心重量。

因此，附加铁耗即为变频器供电与正弦波供电有限元计算之差。

2.3 基于时步有限元的永磁体涡流损耗计算模型

本文采用三维时步有限元法计算了永磁体涡流损耗，具体模型为[2]

式中Jν——第ν次谐波产生的涡流幅值；

σ——永磁体电导率；

V——永磁体体积。

永磁体内由于电流时间谐波产生的涡流损耗增量为变频器供电与正弦波供电有限元计算损耗值之差。

本文计算的电流时间谐波产生的趋肤效应不明显，分析时绕组附加损耗可不予以考虑。另外由于本文所研究的电机采用铝制机壳和端盖，且定、转子铁心没有扣片和端压板，因而，空载运行时结构件中的损耗很小，可以忽略。

2.4 电机参数

本文分析的永磁电机部分参数见表 1，为了缩短计算时间，本文采用单元电机模型来等效电机全模型，其截面图如图1所示。在这里需要说明的是实际铁心损耗需要在有限元计算结果的基础上进行修正，然而齿部与轭部的修正系数不同，因此建模时将定子铁心分成两部分，二者铁耗分开计算。该电机转子磁路结构为表面凸出式，为了改善气隙磁通密度波形，对永磁体进行了削角处理。

图1 电机截面图Fig.1 Cross section of the motor

图2是开关频率为4kHz，调制比为0.7时的空载电流波形及其谐波分布，其有效值为 2.38A。从图中可以看到13、17、25、29和43、47次谐波幅值较大，这些谐波频率集中在开关频率附近，且满足

式中fc——变频器的开关频率；

f0——电机实际运行频率；

b、c为奇偶性相异的正整数。

图2 空载电流波形及其谐波分布Fig.2 No-load current waveform and its harmonic distribution

其中13次时间谐波电流产生的磁场以13倍的同步速相对于定子旋转，以12倍的同步速相对于转子旋转；17次时间谐波产生的谐波磁场以-17（负号表示转向与电机转子转向相反）倍的同步速相对于定子旋转，以-18倍的同步速相对于转子旋转；同理，25、29、43、47次谐波产生的磁场分别以25、-29、43、-47倍同步速相对于定子旋转和24、-30、42、-48倍同步速相对于转子旋转。这些谐波磁场在定、转子铁心、永磁体中不断交变，进而产生大量谐波损耗。

3 计算结果及分析

3.1 变频器供电时电机附加损耗分布规律

图 3是空载变频器供电时（fc=4kHz，a=0.7）电机各部位的附加损耗分布。通过对图中数据分析可知，永磁体上附加损耗占总附加损耗的比例最大，达到 59.0%，其次是定子铁心，其占总损耗的比例为39.9%，转子铁心上最少，只占1.1%；而在整个定子区域，附加铁耗主要集中在定子齿部，约占定子附加铁耗的71.7%。

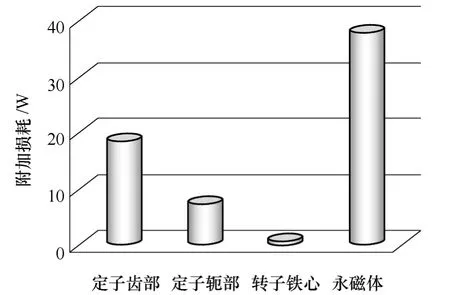
图3 附加损耗分布Fig.3 Distribution of additional loss

3.2 定子铁心各处附加损耗分布情况

由前面分析可知，定子铁心处附加损耗相对较大，于是为了定量研究变频器对铁心损耗分布的影响，现对定子铁心作如下处理：首先将定子铁心划分为4个区域：A代表齿顶，B代表齿身，C代表齿根，D代表轭部。并对四个区域细剖，如图4所示。通过式（5）可计算各区域的附加铁耗。

图4 采样点及其剖分Fig.4 Sampling point distribution and subdivision

表2是A-D点区域附加铁耗的计算结果，通过分析可得电机空载运行时B点区域占定子铁心附加损耗的比重最大，达到 42.4%，D点区域其次，占到28.3%，而其损耗密度最小，C点区域占19.4%，A点区域比重最小，只占9.9%，但是损耗密度最大。

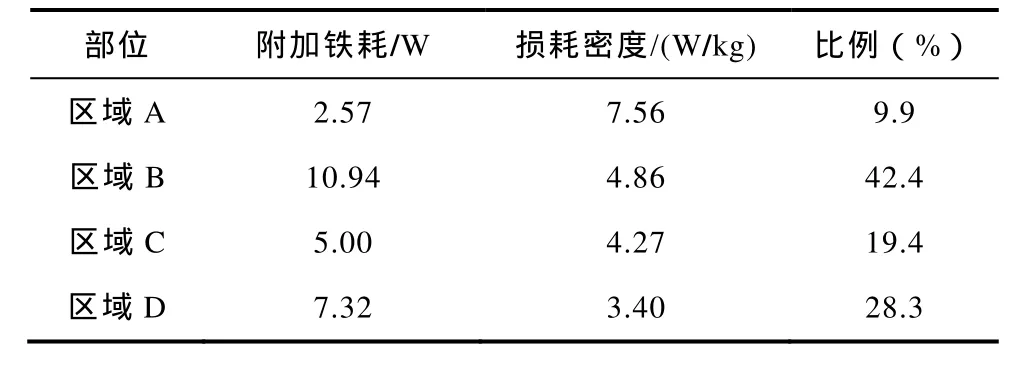
表2 各部位附加铁耗计算结果Tab.2 Calculation result of additional loss in each part

3.3 永磁体涡流损耗分布

为了研究变频器供电时永磁体径向方向上涡流损耗的分布情况，现将4.2kW电机其中一块永磁体作如图5所示处理，具体方法为：将永磁体沿着转子半径方向等分成5块，由外到内分别对其进行编号1～5，对每一块永磁体上的涡流损耗分别计算。

图5 永磁体沿径向等分Fig.5 Aliquots of permanent magnet along radial direction

分别计算了a为 0.6和 0.7，fc为 1kHz、4kHz和8kHz时1～5号永磁体上的涡流损耗，有限元计算结果见表3。当a=0.7，fc由1kHz变到8kHz时，1～5号永磁体内涡流损耗分别减少75.7%、78.2%、78.9%、80.5%和80.3%；当fc=4kHz，a由0.6变到0.7时，1-5号永磁体内涡流损耗分别减少49.1%、50.7%、52.0%、52.6%和 52.2%。此外，无论采用哪种变频器参数1号永磁体（即最外层永磁体）涡流损耗最大，占整块永磁体总损耗的25%以上，而5号永磁体涡流损耗最小；沿半径方向向内永磁体涡流损耗逐渐变小，且变化的幅度趋缓。这是由于高次时间谐波在永磁体内透入深度较浅，次数越高，透入深度越浅，很多高次谐波产生的涡流只在永磁体表面产生涡流回路。图6是运用Ansoft软件模拟的同一时刻5层永磁体内涡流分布，从图中也可以看出涡流从外层向内依次减小。

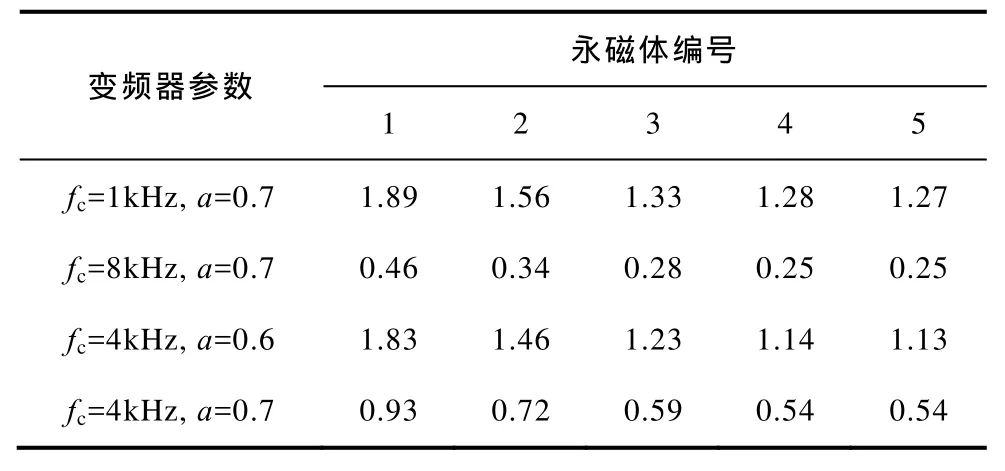
表3 不同变频器参数时各层永磁体涡流损耗分布情况Tab.3 Eddy current loss distribution in each layer of the permanent magnet vs. inverter parameters（单位：W）

3.4 变频器参数对附加损耗的影响

由于电机铁心损耗、永磁体涡流损耗的大小不仅与磁通密度交变频率有关，还与磁通密度幅值有关。因此研究这些损耗，就必须关心铁心各处以及永磁体上的磁通密度分布情况。为了研究变频器参数（包括调制比和开关频率）对电机损耗的影响，在考虑到实验变频器参数可调范围的情况下，取开关频率fc=1kHz、2kHz、3kHz、4kHz、8kHz和 16kHz，调制比a=0.6、0.7、0.8和0.85。

图6 各层永磁体涡流分布Fig.6 Eddy current in each layer

定子铁心上以图1中A点为例，提取其径向磁通密度Br和切向磁通密度Bt，得到不同调制比和开关频率（图中只选取a=0.6、fc=4kHz，a=0.7、fc=4kHz和a=0.7、fc=1kHz三种情况）时的磁通密度轨迹如图7a所示。三种情况下磁通密度轨迹都呈椭圆形，且呈现一定的波动，因为变频器引入了不同次数（开关频率整数倍附近）的时间谐波电流，进而产生许多相对于定子正向、反向旋转的谐波磁场，而且这些谐波磁场不与基波磁场同步旋转，且转速较高，因此相对于正弦波供电，A点磁通密度轨迹在变频器供电时波动较大。不同的是当调制比相同时，开关频率越大，磁通密度波动越小；开关频率相同时，调制比越大，磁通密度波动越小，导致附加损耗也越小。这是因为随着调制比和开关频率的增大，电流波形畸变率变小。类似的，永磁体上取一点 E，转子铁心上取一点 F，分别得到不同变频器参数时的磁通密度随时间变化如图7b、7c所示。可以得到与A点类似的结论：相同开关频率时，磁通密度波动随调制比的增大而减小；相同调制比时，磁通密度波动随开关频率的增大而减小。

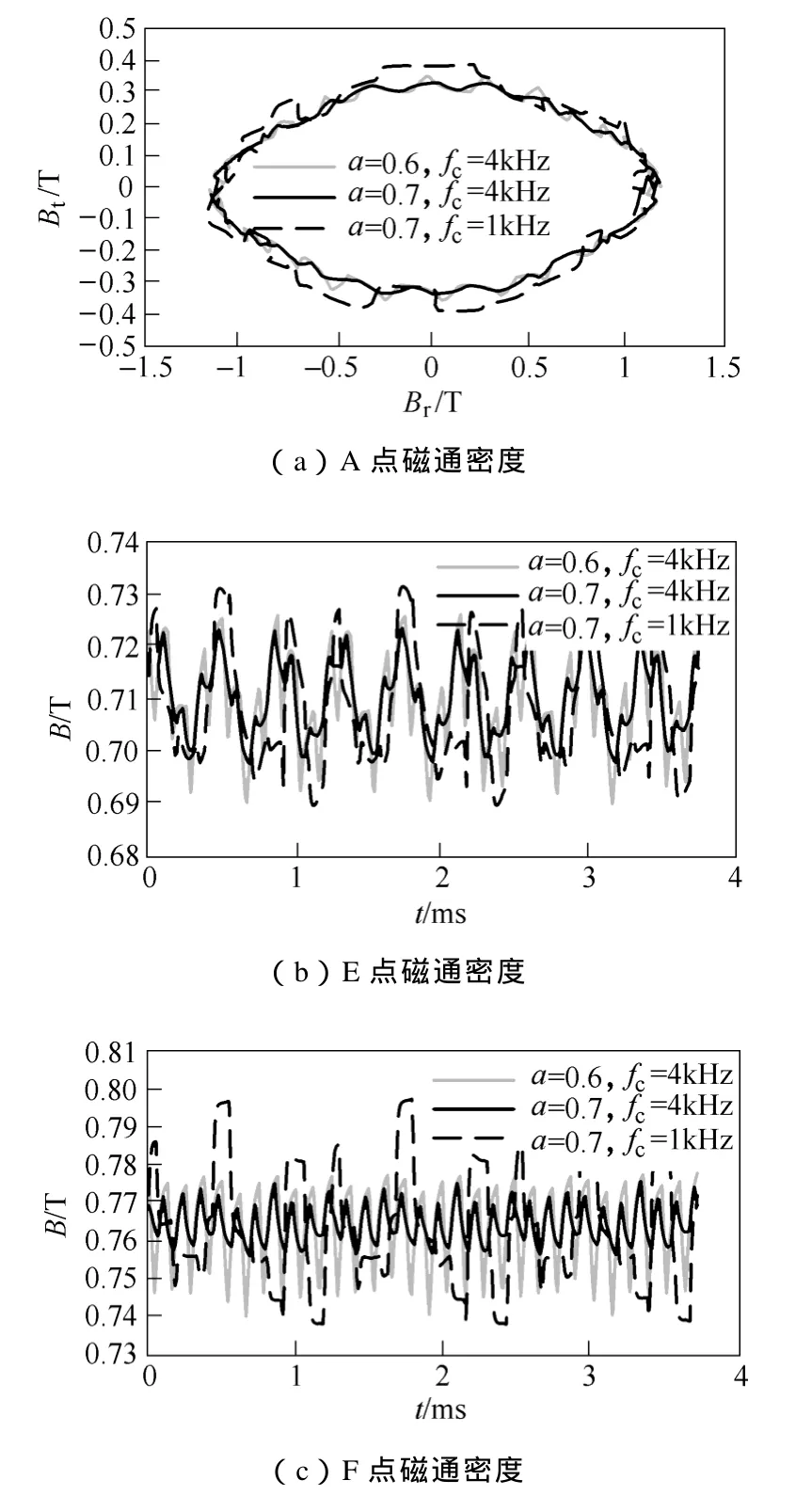
图7 不同变频器参数时各点磁通密度变化Fig.7 Flux density of each point vs. inverter parameters

图8是电机定、转子铁心，永磁体中的附加损耗随变频器参数的变化关系。随着调制比和开关频率的增大，三种附加损耗都呈减少趋势，且以fc=3kHz为分界点，fc＜3kHz时附加损耗减少幅度较大，fc从1kHz增加到3kHz，每增加1kHz，定子铁心附加损耗平均降低 24.4%，转子铁心附加损耗平均降低27.1%，永磁体附加损耗平均降低17.1%，总附加损耗平均降低 20.7%；fc＞3kHz时，附加损耗减少幅度趋于平缓，每增加1kHz，定子铁心附加损耗平均降低 6.2%，转子铁心附加损耗平均降低4.3%，永磁体附加损耗平均降低6.9%，总附加损耗平均降低6.5%。而当a从0.6到0.85每增加0.1时，定子铁心附加损耗平均降低 13.1%，转子铁心附加损耗平均降低 24.5%，永磁体附加损耗平均降低22.1%，总附加损耗平均降低18.7%，且各部分损耗变化逐渐趋缓。其原因是这两个变频器参数增加到一定值后，电流波形畸变率逐渐趋于稳定，铁心和永磁体中的磁通密度波动也逐渐趋于稳定，附加损耗变化也随之稳定。此外，从图中还可以看出变频器供电时永磁体上附加损耗最大，定子铁心其次，转子铁心上最小。可见，对于表面式永磁电机，时间谐波对永磁体影响最大。

图8 各损耗随变频器参数变化Fig.8 Each loss vs. inverter parameters

3.5 气隙长度对附加损耗的影响

保持永磁体的极弧系数和定子侧的设计尺寸不变，取气隙长度分别为 1.0mm、1.3mm、1.5mm、1.8mm和2.0mm，改变永磁体的磁化方向长度（hM）并使其与气隙长度的比值保持恒定，这样可以在改变气隙长度的同时保证空载气隙磁通密度和空载反电动势基本不变[16]。图9给出了电机在空载运行时各部分附加损耗随气隙长度的变化关系曲线。从图中可以看出定子铁心、转子铁心、永磁体附加损耗都随气隙长度的增加而减小，δ从1mm到2mm，平均每增加0.1mm，定子铁心附加损耗降低4.3%，转子铁心附加损耗降低 8.4%，永磁体附加损耗降低6.0%，总附加损耗降低5.4%。因为随着气隙长度的增加，时间谐波电流产生的谐波磁场影响减弱，谐波磁通密度幅值减小。

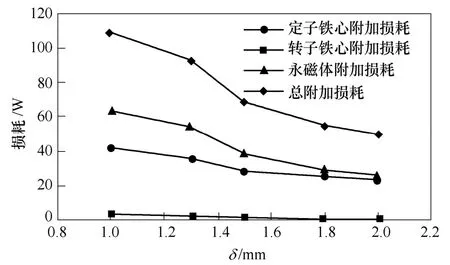
图9 各部分损耗随气隙长度变化Fig.9 Loss in each part vs. air-gap length

为了说明不同气隙长度时电机各部位附加损耗发生变化的原因，图10给出了各部位所选取点（A、E、F）处的磁通密度变化。从图中可以看到，气隙磁通密度从1.0mm增加到2.0mm，以上各点处的磁通密度波动逐渐减小。

图10 不同气隙长度时各点磁通密度变化Fig.10 Flux density variation of each point vs. air-gap length

3.6 转子磁路结构对附加损耗分布的影响

本部分内容研究了不同转子磁路结构（如图11所示）时的电机附加损耗分布差异。其中图11a是表面式结构，图11b是内置式结构，两种结构气隙长度和气隙磁通密度相同。

图11 两种不同转子磁路结构Fig.11 Two kind of magnetic structure

图 12为两种不同磁路结构下时间谐波磁通路径，对于表面式结构而言，磁通路径包括两条：

（1）定子齿—永磁体—转子铁心—定子齿。

（2）定子齿—转子铁心—定子齿。

而对于内置式结构，多了一条路径 c（定子齿—转子铁心表层—定子齿）。在内置式结构中电流时间谐波磁通更多地通过转子铁心形成闭合回路，而不经过永磁体，于是永磁体涡流损耗相对于表面式大大减少。

图12 时间谐波磁通路径Fig.12 Flux path of time harmonic

图 13是两种转子磁路结构下电机各部位的附加损耗分布对比图，图14给出了各部分附加损耗占比。从图中可以看出不同磁路结构电机各部分损耗占比不尽相同。其中内置式结构定子铁心处附加损耗占总损耗比例最大，达到 59.1%，永磁体其次，转子铁心最小，只占9.7%；而表面式结构永磁体内附加损耗占比最大，定子铁心其次，转子铁心也是最小。就数值而言，内置式结构定子铁心附加损耗大于表面式，因为表面式结构等效气隙较大，时间谐波电流产生的磁场影响减弱，谐波磁通密度幅值减小，于是定子附加铁耗也较小；永磁体内附加损耗则是表面式结构较大，因为由上面分析可知，内置式结构中电流时间谐波磁通更多地通过转子铁心形成闭合回路，而不经过永磁体。尽管两种结构转子铁心附加损耗占比都是最小，但是由于表面式结构等效气隙较大，数值上比内置式结构小。就总附加损耗而言，内置式结构总损耗大于表面式。

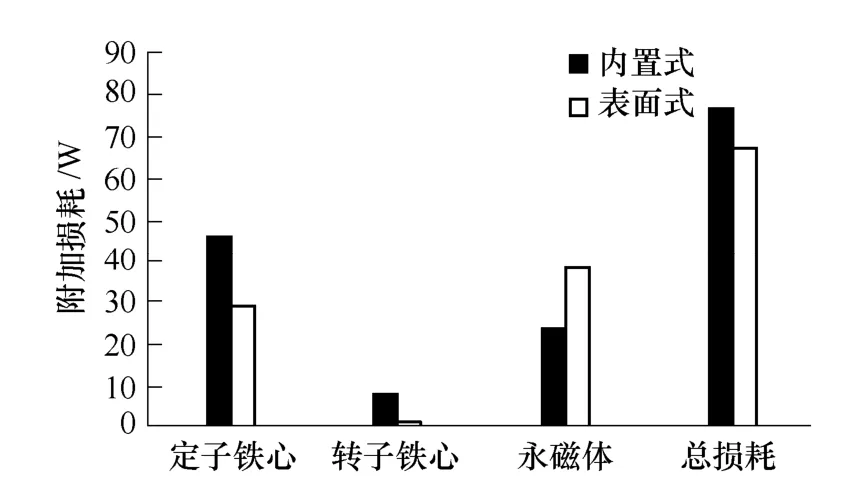
图13 不同磁路结构下的附加损耗Fig.13 Additional loss under different magnetic structures

图14 附加损耗比例Fig.14 Percentage of additional loss

4 实验

为了验证变频器参数对附加损耗影响规律以及时间谐波幅值与附加损耗的关系，本文采用的实验原理如图 15所示，实验装置如图 16所示。图 15中虚线框部分仅在研究调制比这一参数的影响时用到，在研究开关频率参数实验时可移除。

图15 实验原理图Fig.15 Schematic diagram for test

图16 实验装置图Fig.16 Equipment of measuring system

变频器供电实验方法具体为：首先改变变频器参数，再合上开关1，断开开关2，待电机转稳后通过数字功率计读取并记录电压、电流、输入功率。正弦波供电实验方法具体为：合上开关 2、断开开关1，调节调压器 2使得数字功率计电压读数和变频器供电相同，待电机转稳后读取并记录电压、电流、输入功率。正弦波供电时的正弦电源由如图 16b所示装置提供，可以看到由一台直流电机拖动一台永磁电机发电，进而供给被试电机。变频器供电空载铁耗减去正弦波供电空载铁耗即为附加损耗值。采用上述方法计算得到不同变频器参数时附加损耗计算值Pf、实验值Pt以及实验值与计算值之比λ见表4、表5。表中所测试的三台电机定转子具有相似的几何外形和结构工艺。由结果可知，对于 4.2kW电机，λ在1.1～1.4之间；6.9kW电机λ在1.2～1.9之间；而9.42kW电机在1.0～1.5之间。计算值与实测值一致性较好，由于没有计及绕组中的附加铜耗、结构件中的涡流损耗以及铁心压装工艺等对损耗的影响，因而计算值略小于实测值。对于本文所研究的采用8极36槽、不等气隙表面式磁极结构、铝制机壳和端盖电机，λ平均值约为1.38。

表4 不同开关频率（调制比恒定）时附加损耗计算值与实验值对比Tab.4 Value comparison between calculation and test of additional losses at differentfc（a is a constant）

表5 不同调制比（开关频率恒定）时附加损耗计算值与实验值对比Tab.5 Value comparison between calculation and test of additional losses at differenta（fcis a constant）

5 结论

本文以一台4.2kW、8极表面式永磁电机为例，运用时步有限元法分析了不同变频器参数、气隙长度时，电机定转子铁心、永磁体上的磁通密度分布情况，计算了各部位的附加损耗；研究了表面式和内置式磁路结构下电机附加损耗分布差异；最后通过三台结构相似样机实验，验证附加损耗随变频器参数的变化规律。得到如下结论：

（1）fc＜3kHz时，平均每增加 1kHz，总附加损耗降低20.7%；fc＞3kHz时，平均每增加1kHz，总附加损耗降低6.5%。而当a从0.6到0.85每增加0.1时，总附加损耗降低18.7%；δ从1mm到2mm，平均每增加0.1mm，总附加损耗降低5.4%。

（2）内置式结构附加损耗主要集中在定子铁心上，而表面式结构主要集中在永磁体上；对于转子铁心附加损耗，内置式结构比重比表面式大，而永磁体涡流损耗内置式较小。

（3）通过对4.2kW、6.9kW和9.42kW三台采用 8极 36槽、不等气隙表面式磁极结构、铝制机壳和端盖样机的分析计算与测试，得到了在不同变频器参数下附加损耗实验值与计算值之比λ，三台电机λ平均值约为1.38。对于采用相近结构、工艺以及相近功率等级的电机，可采用该系数对电机的附加损耗值进行预估。

[1] Zhu Baofeng, Bai Baodong, He Huiming. Effect of inverter parameters on the eddy current losses in induction motor fed by PWM inverter[C]. International Conference on Electrical Machines and Systems, 2008:4240-4243.

[2] Katsumi Yamazaki, Atsushi Abe. Loss investigation of interior permanent-magnet motors considering carrier harmonics and magnet eddy currents[J]. IEEE Transactions on Magnetics, 2009, 41(5): 659-665.

[3] Javad Fouladgar, Eric Chauveau. The influence of the harmonics on the temperature of electrical machines[J]. IEEE Transactions on Magnetics, 2005, 41(5):1644-1647.

[4] 韩静静. PWM逆变器供电对异步电动机铁心损耗影响的研究[D]. 北京: 北京交通大学, 2011.

[5] 韩力, 谢李丹, 张桂娟. 变频器参数对永磁同步发电机定子损耗的影响[J]. 电机与控制学报, 2010,14(12): 75-81.

Han Li, Xie Lidan, Zhang Guijuan. Influence of converter parameters on stator losses of permanent magnet synchronous generator[J]. Electric Machines and Control, 2010, 14(12): 75-81.

[6] 黄平林, 胡虔生, 崔杨, 等. PWM 逆变器供电下电机铁心损耗的解析计算[J]. 中国电机工程学报,2007, 27(12): 19-23.

Huang Pinglin, Hu Qiansheng, Cui Yang, et al. Analytical calculation of the iron losses of electric machine fed by PWM inverter[J]. Proceedings of the CSEE,2007, 27(12): 19-23.

[7] Aldo Boglietti, Andrea Cavagnino, Dan M Ionel, et al.A general model to predict the iron losses in PWM inverter fed induction motors[J]. IEEE Transactions on Industry Applications, 2010, 46(5): 1882-1890.

[8] 赵海森, 罗应立, 刘晓芳, 等. 异步电机空载铁耗分布的时步有限元分析[J]. 中国电机工程学报,2010, 30(30): 99-106.

Zhao Haisen, Luo Yingli, Liu Xiaofang, et al. Analysis on no-load iron losses distribution of asynchronous motors with time-stepping finite element method[J].Proceedings of the CSEE, 2010, 30(30): 99-106.

[9] Boglietti A, Ferraris P, Lazzari M, et al. Change of the iron losses with the switching supply frequency in soft magnetic materials supplied by PWM inverter[J].IEEE Transactions on Magnetics, 1995, 31(6): 4250-4252.

[10] Katsumi Yamazaki, Atsushi Abe. Loss analysis of interior permanent magnet motors considering carrier harmonics and magnet eddy currents using 3-D FEM[C]. Electric Machines and Drives Conference, 2007:905-909.

[11] 韩守亮, 崔淑梅, 王铁成, 等. 分数槽集中绕组永磁电机在模块化级联电机系统上的应用[J]. 电工技术学报, 2013, 28(3): 9-16.

Han Shouliang, Cui Shumei, Wang Tiecheng, et al.Application of fractional-slot concentrated winding permanent magnet machines in modular cascade machine System[J]. Transactions of China Electrotechnical Society, 2013, 28(3): 9-16.

[12] 孔晓光, 王凤翔, 邢军强. 高速永磁电机的损耗计算与温度场分析[J]. 电工技术学报, 2012, 27(9):166-173.

Kong Xiaoguang, Wang Fengxiang, Xing Junqiang.Losses calculation and temperature field analysis of high speed permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 166-173.

[13] 邹继斌, 李建军, 徐永向, 等. 驱动方式对永磁无刷直流电机损耗的影响[J]. 电工技术学报, 2011,26(9): 43-47.

Zou Jibin, Li Jianjun, Xu Yongxiang, et al. Influences of drive strategies on the loss of permanent magnet brushless direct current motor[J]. Transactions of China Electrotechnical Society, 2011, 26(9): 43-47.

[14] 辜承林, 陈乔夫, 熊永前. 电机学[M]. 武汉: 华中科技大学出版社, 2010.

[15] 陈世坤. 电机设计[M]. 北京: 机械工业出版社,2000.

[16] 田占元, 祝长生, 王玎. 飞轮储能用高速永磁电机转子的涡流损耗[J]. 浙江大学学报, 2011, 45(3):451-457.

Tian Zhanyuan, Zhu Changsheng, Wang Ding. Rotor eddy current loss in high speed permanent magnet motors for flywheel energy storage system[J]. Journal of Zhe Jiang University, 2011, 45(3): 451-457.