脉振高频信号注入法误差分析
刘海东 周 波 郭鸿浩 刘 兵 李 洁 徐学海 时仁帅
(1. 江苏省新能源发电与电能变换重点实验室(南京航空航天大学) 南京 210016 2. 深圳市蓝海华腾技术股份有限公司 深圳 518055)
1 引言
永磁同步电机驱动通常需要通过位置传感器获取转子的位置和速度信号。机械位置传感器的存在增加了系统的复杂性和成本,降低了系统的可靠性,同时也限制了永磁同步电机在一些特殊场合的应用。基于脉振高频电压信号注入法的无位置传感器控制技术通过在估计转子位置注入脉振高频电压信号,检测其交轴电流响应,利用电机的结构凸极或饱和凸极特性估计转子位置[1-4]。该方法简单易行、快速性好、具有较高的精度且无需精确电机参数,已经引起了相关领域研究人员的广泛关注[5]。
永磁同步电机无位置传感器控制的位置估计误差大小是评价其性能的重要指标。虽然理论上讲基于脉振高频电压信号注入法的永磁同步电机无位置传感器控制系统在稳态时系统误差为零,然而,在大量的研究实验中发现,在该方法的应用过程中误差总是难以避免。当前人们对于位置估计误差的来源多归因于电机的高频信号模型不够精确。为了补偿由于理论推导时的工程近似或者电机运行时参数的变化所导致的误差,一种思路是建立更为复杂精确的永磁同步电机高频信号模型[6-12],在此基础上进行控制或补偿;另一种思路是将脉振高频信号注入法与自适应控制方法或滑模观测器等现代控制理论相结合[13-16]。这些研究工作在一定程度上解释了脉振高频信号注入法误差的来源,并针对性地提出了减小位置估计误差的方法。
然而,当前关于脉振高频信号注入法位置估计误差的研究工作仍有不足之处。首先,位置估计误差的来源并不能简单归因于理论推导时的数学建模不够精确。实际操作过程中的无位置传感器控制系统非常复杂,即使数学模型足够精确,由于数字控制器的离散化控制,传感器精度有限,以及线路传输延时等因素仍可能引入误差。其次,无论是建立更加复杂的数学模型还是与现代控制理论的结合都牺牲了脉振高频信号注入法简单易行、对电机参数变化不敏感的优点。
本文旨在保留简化的表贴式(SPM)永磁同步电机高频信号模型的基础上,分析其他引入位置估计误差的因素。在综合分析一些系统参数对位置估计误差的影响后,给出含有这些参数的位置估计误差的解析表达式;最后应用该误差表达式指导脉振高频电压信号注入法无位置传感器控制系统的参数选择,以达到减小位置估计误差的效果。
2 脉振高频信号注入法基本理论
根据文献[1],永磁同步电机在高频信号下的模型可等效为式(1)所示的纯电感模型

为了简化后续运算与推导,将式(1)写成如下相量形式
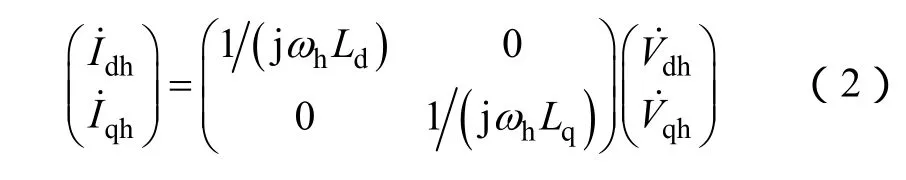
式中ωh——脉振高频电压信号角频率。
假设电机转子实际位置(d轴与 a相绕组轴线夹角)为θ,电机转子估计位置(轴与a相绕组轴线夹角)为,转子估计位置误差Δθ=θ-。各角度与坐标轴对应关系如图1所示。
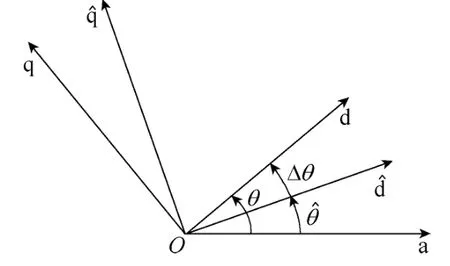
图1 估计位置与实际位置Fig.1 Real and estimated positions
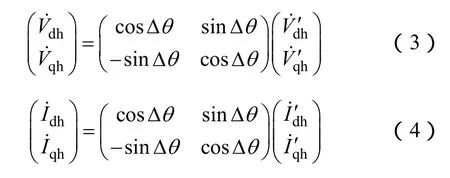
将式(3)、式(4)代入式(2)可得
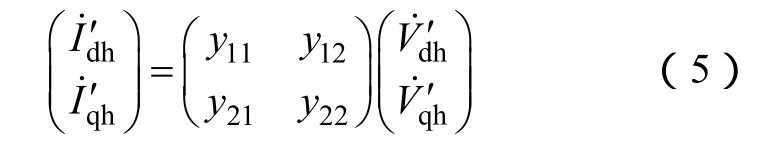
式中
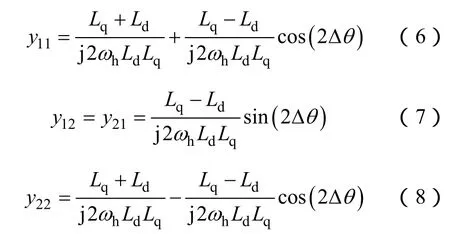
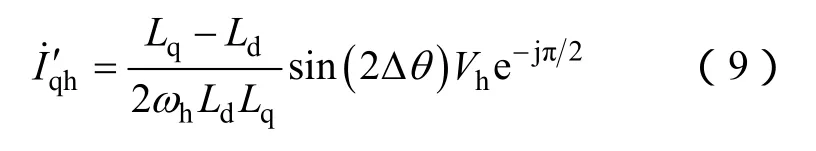
记Ld-Lq=ΔL,对于内嵌式和内埋式永磁同步电机,ΔL大小由电机本身凸极结构决定。对于表贴式永磁同步电机,未注入脉振高频电压时Ld=Lq=L;注入脉振高频电压后,脉振高频电流会使d轴主磁路饱和,使得Ld<Lq,该现象称为“饱和凸极效应”。
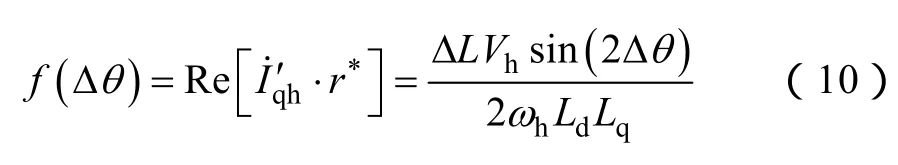
式中,*表示共轭;Re[ ]表示取实部。
在实际操作中获得f(Δθ)的方式为:通过电流传感器检测电机相电流,之后通过坐标变换得到轴电流,将轴电流通过选通频率为fh的带通滤波器(BPF)后得到高频电流,与 2 sin(ωht)相乘后通过低通滤波器(LPF)即得到f(Δθ)。
将f(Δθ)作为误差信号输入PI调节器构成位置估计系统闭环,系统稳定时f(Δθ)=0,故Δθ=0。如此便可实现永磁同步电机的无位置传感器控制。系统原理图如2所示。
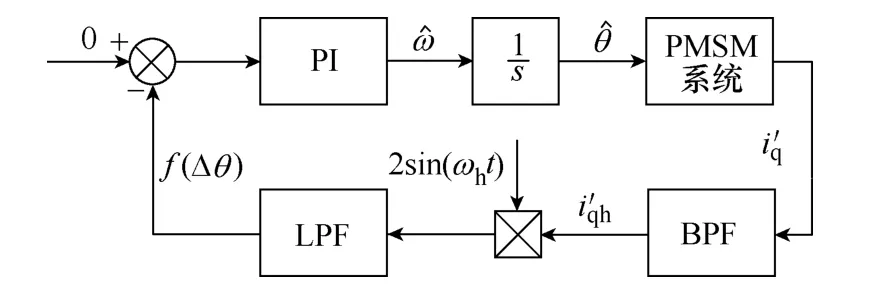
图2 位置估计系统框图Fig.2 Diagram of position estimation system
3 脉振高频电压分析
以变量ηx表示x(x∈ { a, b ,c}) 相桥臂上管工作状态,上管处于导通状态时ηx=1,处于关断状态时ηx=0。永磁同步电机轴脉振高频电压、可表示为为坐标变换向量,表达式为

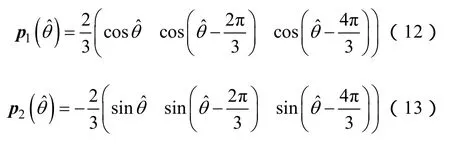
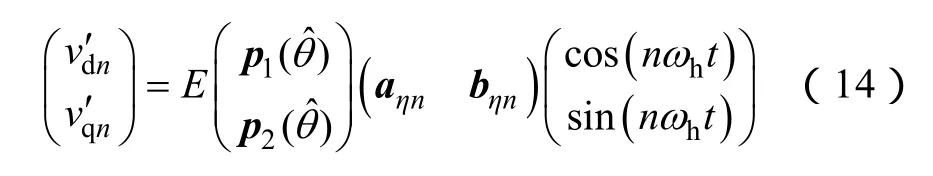
式中
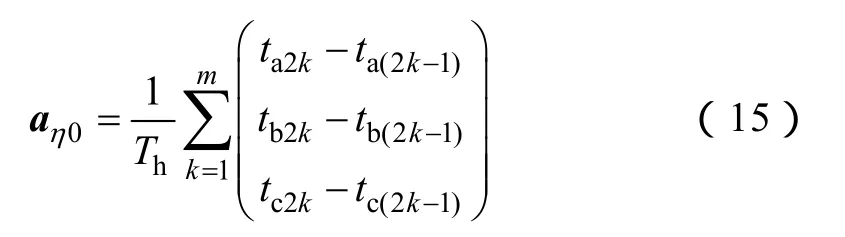
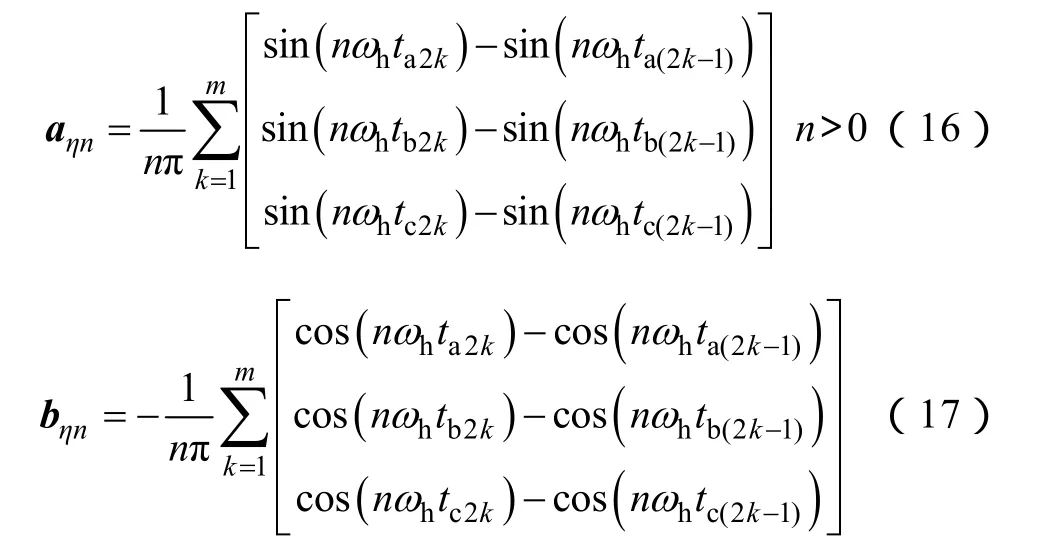
ta(2k-1)、tb(2k-1)和tc(2k-1)是在第k(k=1, 2, …,m)个开关周期内,逆变器a、b和c三相桥臂上管导通时刻;a2kt、b2kt和c2kt为关断时刻。m是在一个脉振高频信号周期Th内,每个开关管导通和关断的次数。假设逆变器开关频率为fs,且是高频信号频率的整数倍,则m=fsfh。由于一个信号周期内,每个开关管导通和关断的次数均为m,故此处用奇数下标2k-1表示开通时刻,偶数下标2k表示关断时刻;下标abc表示对应的逆变器abc相桥臂。
为了求得逆变器各管开通关断时刻的值,需要借助SVPWM的基本理论。因为其推导过程过于复杂,在此仅给出结果。在第k个开关周期逆变器各管开关时刻见表1。表中扇区I-VI为注入电压矢量扇区,ikt(i=1, 2, …, 6)为开关时刻。各扇区与边界基本电压矢量对应关系如图3所示。
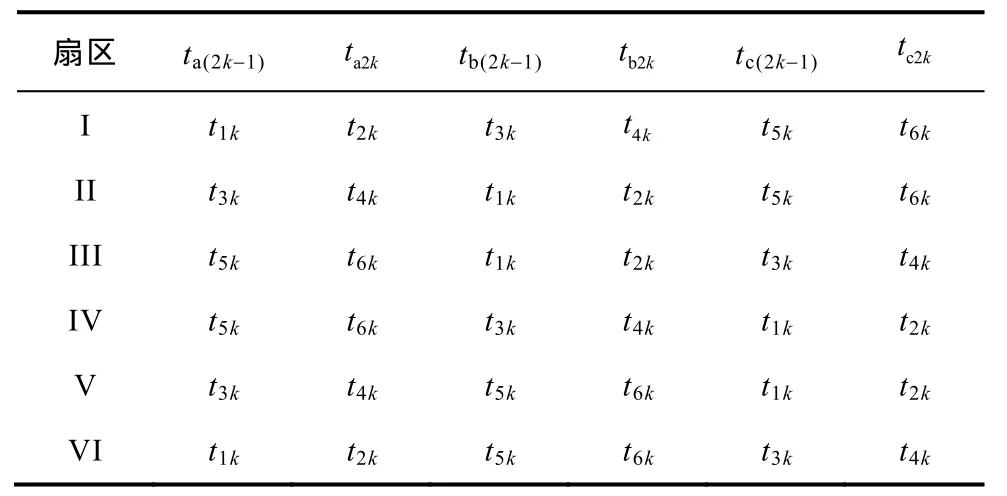
表1 逆变器各管开关时刻表Tab.1 Inverter switching time table
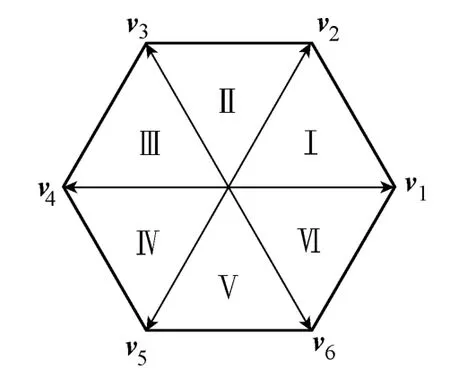
图3 扇区与基本电压矢量图Fig.3 Diagram of sections and basic voltage vectors
确定表1中tik(i=1, 2, …, 6)的表达式需借助不考虑数字控制器离散化控制时钟周期Tc的理想情况下开关时刻的值
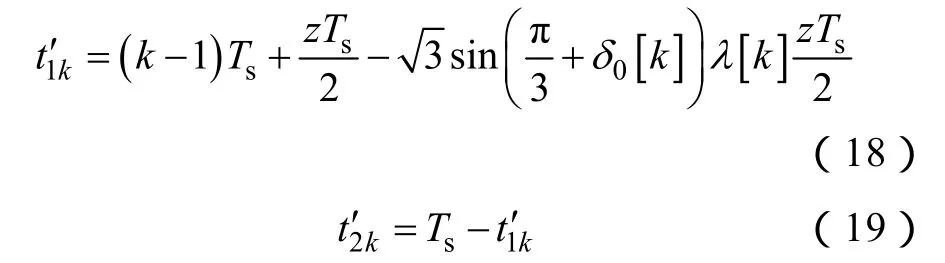
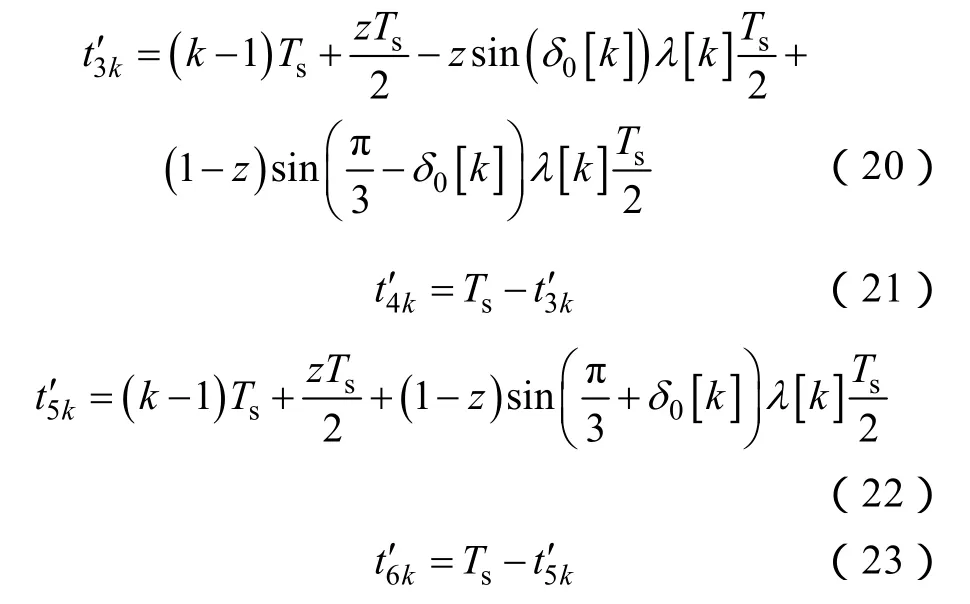
式中,λ[k] 为调制系数,其表达式为
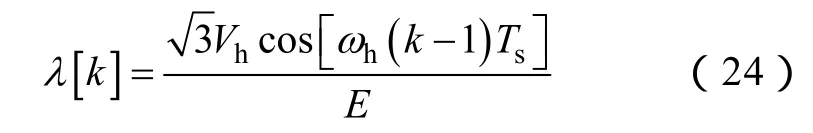
z表示一个周期内逆变器上管均关断的时间占逆变器各桥臂输出电压均为0的时间的比例。通常取z=0.5。δ0[k]是角度中间变量,其在不同扇区与第k个开关周期注入的电压矢量在αβ坐标系下的角度δ[k] 关系见表2。

表 2 δ0[k]-δ[k]对照表Tab.2δ0[k]-δ[k] look-up table
实际操作中,由于各管开关时间只能是数字控制器时钟周期Tc的整数倍,实际开关时刻应修正为
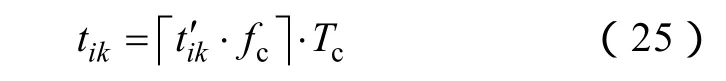
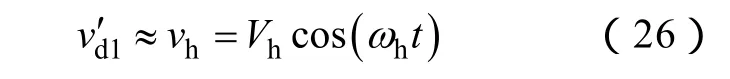
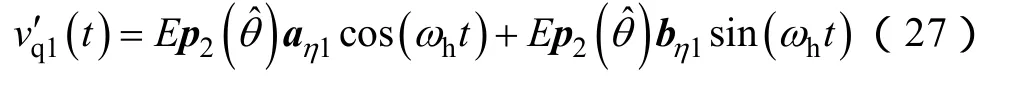
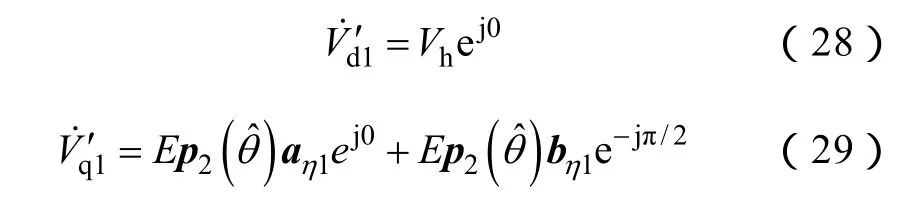
4 位置估计误差理论分析
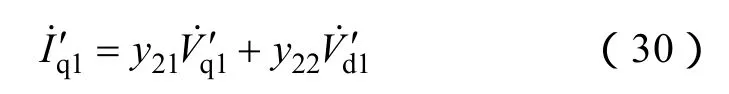
位置估计系统PI调节器实际输入f'(θΔ)为
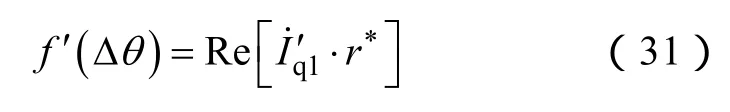
将式(7)、式(8)、式(28)、式(29)代入式(31)并化简可得
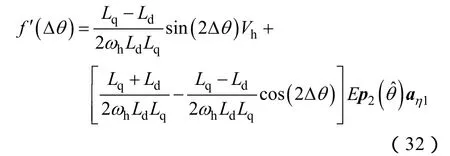
位置估计系统达到稳态时由f'(θΔ)=0可得
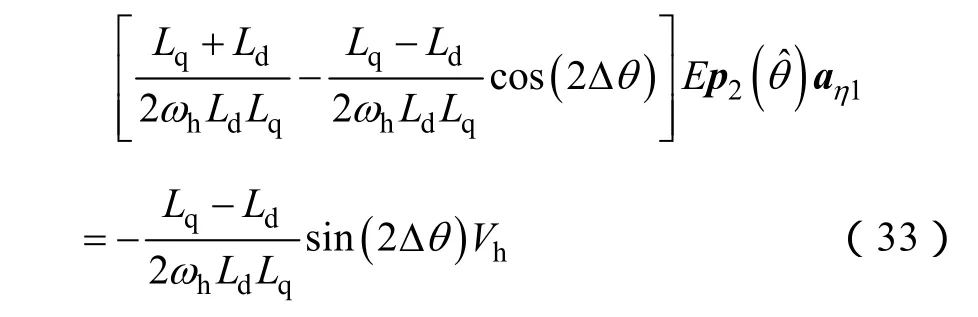
Δθ很小时 s in(2Δθ)≈2Δθ, c os(2Δθ)≈1, 式(33)可化简为
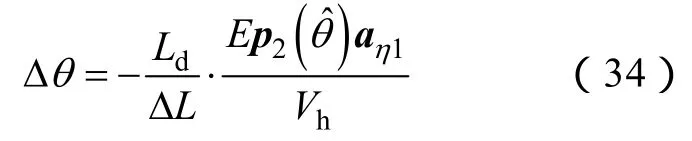
式(34)即为最终的脉振高频信号注入法位置估计误差公式。Ld表示永磁同步电机的d轴电感。ΔL表示dq轴电感之差。Vh表示采用脉振高频信号注入法在轴注入的脉振高频电压的幅值。Ep2()/Vh表示轴脉振高频电压基波中与同相位的分量。
Ld/ΔL反应了永磁同步电机的凸极特性。对于表贴式永磁同步电机Ld/ΔL由注入信号引起的“饱和凸极效应”决定。
Ep2()/Vh反应了轴与轴同相位分量脉振高频电压基波幅值之比。其值由三相逆变器直流母线电压E,位置估计系统最终的收敛角度,d轴注入脉振高频电压幅值Vh,以及逆变器开关函数矢量的基波余弦分量1ηa共同决定。1ηa的表达式可根据式(16)得到。
5 位置估计误差数值分析
由于Ep2()/Vh一项过于复杂,无法直接凭借解析式看出各参数对位置估计误差的影响,故本节采用数值分析的方法,以得到较为直观的结论。
根据[3]中的研究结果,应用脉振高频电压信号注入法对表贴式永磁电机进行无位置传感器控制时,Ld/ΔL的数量级约为 100。在此取Ld/ΔL=400,并将该值应用于后续的位置估计误差Δθ计算。
以下总共进行a、b、c、d四组数值计算。四组数值计算中相同的系统参数依照后文实验系统选择如下:三相逆变器开关管开关频率fs=20kHz;d轴注入的脉振高频信号频率fh=1kHz;Ld/ΔL=400;z=0.5。各组计算的逆变器直流母线电压E,脉振高频信号幅值Vh和控制器时钟频率fc见表 3。表中fc=∞表示数字控制器主频无穷大的理想情况。
根据四组计算结果所得位置估计误差Δθ随着转子位置角度ˆθ的变化关系如图4所示。
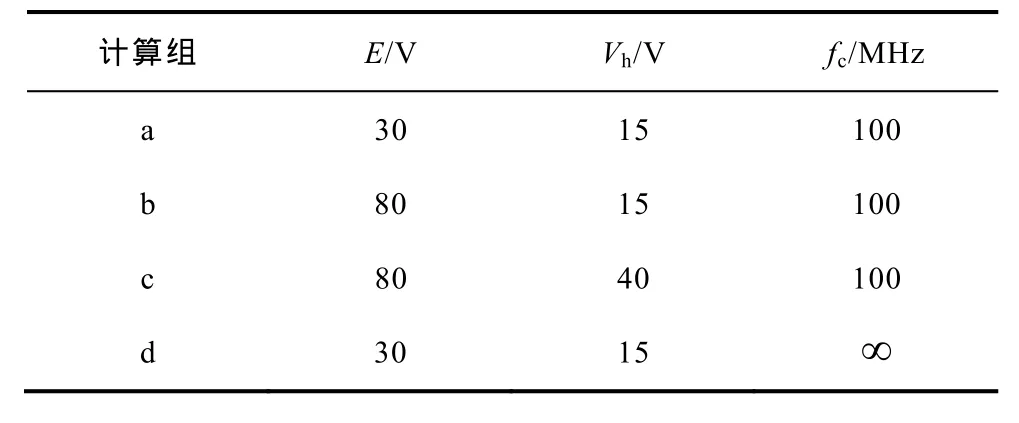
表3 计算组参数对照表Tab.3 Calculating group parameter table
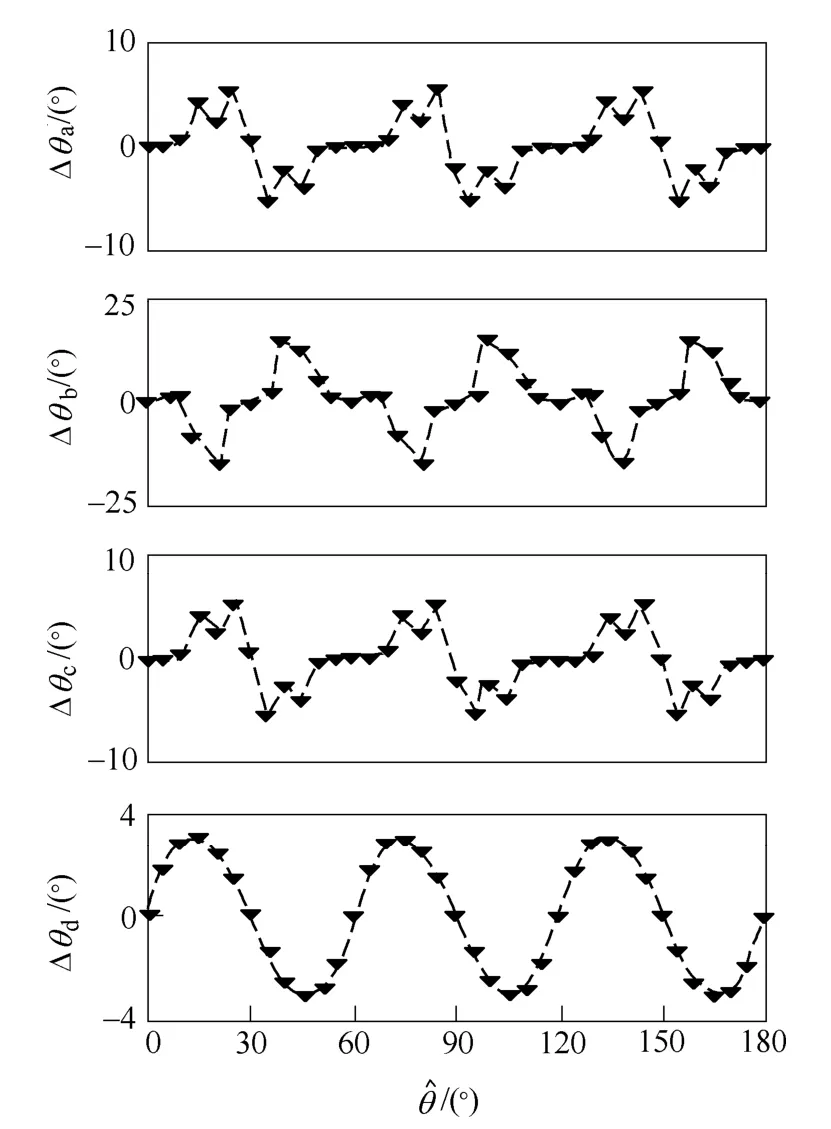
图4 Δθ - 关系数值分析结果Fig.4 Numerical analysis results of Δθ - relation
图 4 中Δθa、Δθb、Δθc、Δθd分别为 a、b、c、d四组数值计算中所对应的位置估计误差Δθ。由图 4可见,Δθ随θ的变化具有周期性,周期约为60°。对比a和d两组分析结果可得,位置估计误差最大值随着控制器时钟频率fc的增大而减小。对比a和b两组分析结果可得,注入脉振高频电压幅值Vh一定,随逆变器直流母线电压E增大而增大。对比a和c两组分析结果可得,E/Vh固定,若Ld/ΔL恒定,则不随E和Vh改变;对于表贴式永磁同步电机,Vh增大会强化“饱和凸极效应”,Ld/ΔL减小,故E/Vh固定,随E和Vh增大而减小。
综上可得以下结论:为了减小位置估计误差Δθ,应当增大控制器的主频fc,降低三相逆变器直流母线电压E与注入脉振高频电压信号幅值Vh之比E/Vh的同时增大E和Vh。E/Vh的最小值是逆变器直流母线电压与采用SVPWM策略所能获得的最大电压矢量幅值之比,该项大小由电压调制系数λ≤1这一关系决定,根据式(24)可得
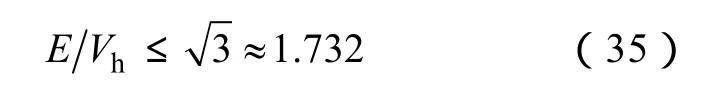
为了验证以上分析的正确性,第6节对其进行实验验证。
6 误差分析理论实验验证
实验中所用表贴式永磁同步电机参数如下:额定功率PN=800W,额定转速nN=3 000r/min,额定电压UN=310V,极对数p=2。数字控制器主频fc=100MHz。电机空载运行,实验平台如图5所示。电机采用基于脉振高频电压信号注入法的无位置传感器矢量控制,给定转速为20r/min,稳定运行时电机实际位置θ、估计位置、实际转速n、估计转速波形如图6所示。应用图5所示实验平台,对上节a、b、c三组数值计算进行实验验证。实验中 a、b、c三组系统参数的选择与上节表3中数值计算a、b、c三组系统参数相同,结果如图7所示。

图5 表贴式永磁同步电机无位置传感器控制实验平台Fig.5 Experimental platform of SPM (surface mounted permanent magnet synchronous motor) sensorless control
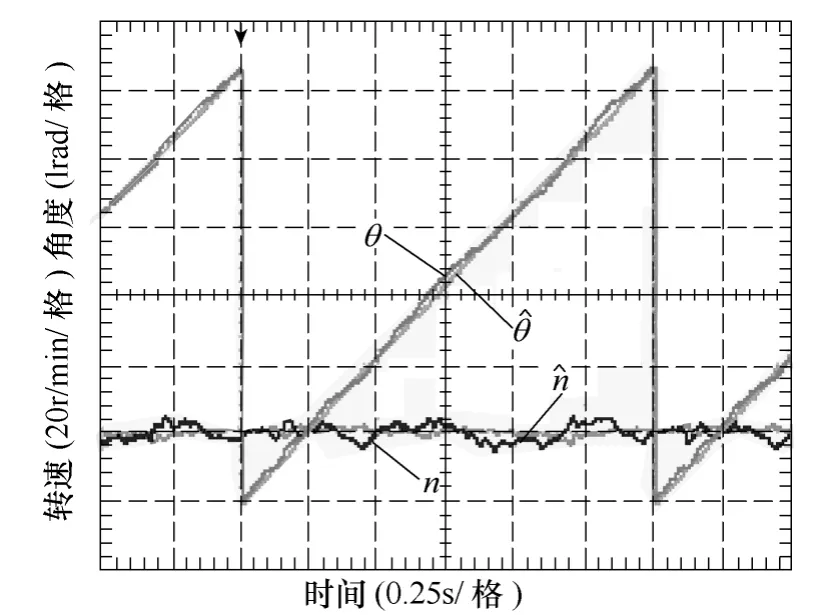
图6 无位置传感器控制电机位置及转速波形Fig.6 Rotor position and rotational speed of SPM under sensorless control condition
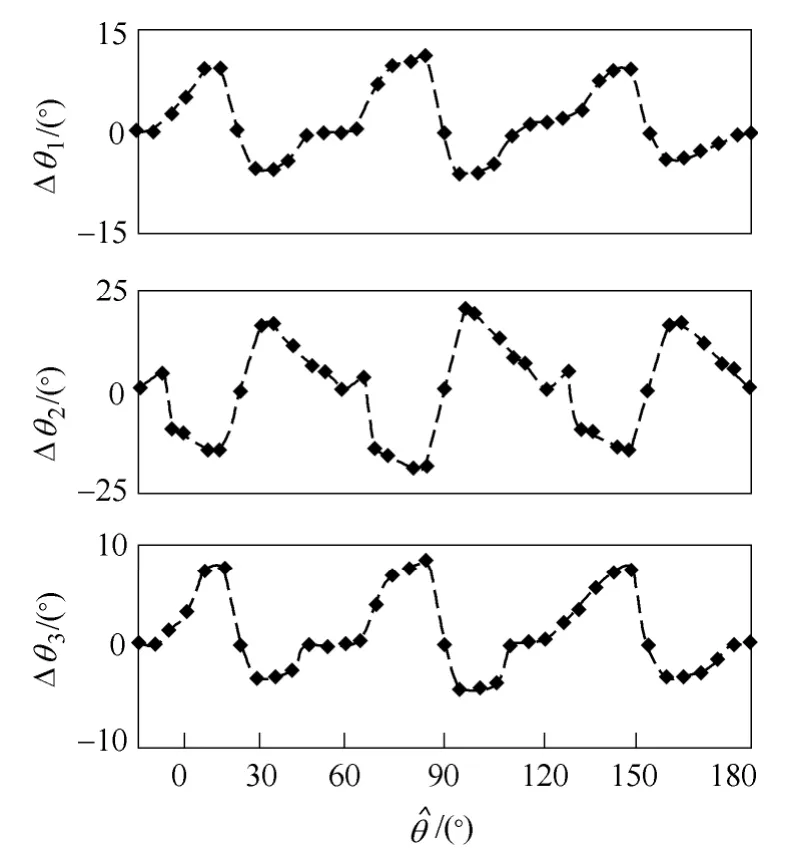
图7 Δθ - 关系实验结果Fig.7 Experimental results of Δθ - relation
图 7 中Δθ1、Δθ2、Δθ3分别对应图 4中Δθa、Δθb、Δθc。由实验结果可见,Δθ随θ近似以 60°的周期变化。对比Δθ1和Δθ2可见,注入脉振高频电压幅值Vh一定,随逆变器直流母线电压E增大而增大。对比Δθ2和Δθ3可见,对于表贴式永磁同步电机,E/Vh固定,随E和Vh增大而减小。
综上可得,实验结果与理论分析一致,本文提出的误差分析理论得到了验证。
7 结论
本文主要对脉振高频电压信号注入法永磁同步电机无位置传感器控制系统位置估计误差做了详细的分析,得到如下结论:为了减小脉振高频电压信号注入法永磁同步电机无位置传感器控制系统的位置估计误差Δθ,应当如下:
(1)增大控制器的主频fc。
(2)降低三相逆变器直流母线电压E与注入脉振高频电压信号幅值Vh之比E/Vh(下限为1.732)。
(3)对表贴式永磁同步电机降低E/Vh的同时增大E和Vh各自的值。
[1] 王高林, 杨荣峰, 李刚, 等. 基于高频信号注入的IPMSM 无位置传感器控制策略[J]. 电工技术学报,2013, 27(11): 62-68.
Wang Gaolin, Yang Rongfeng, Li Gang, et al. Position sensorless control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2013, 27(11): 62-68.
[2] 王高林, 杨荣峰, 于泳, 等. 内置式永磁同步电机无位置传感器控制[J]. 中国电机工程学报, 2011,31(30): 93-98.
Wang Gaolin, Yang Rongfeng, Yu Yong, et al. Position sensorless control for interior permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2011,31(30): 93-98.
[3] Yang Shih Chin,Lorenz Robert D. Comparison of resistance-based and inductance-based self-sensing controls for surface permanent-magnet machines using high-frequency signal injection[J]. IEEE Transactions on Industry Applications, 2012, 48(3): 977-986.
[4] Koschik S, van Treek D, De Doncker R W. Evaluation of methods for the operation of PMSM without position sensor[C]. Power Electronics and ECCE Asia (ICPE& ECCE), IEEE, 2011: 1250-1256.
[5] Chen J L, Tseng S K, Liu T H. Implementation of high-performance sensorless interior permanent-magnet synchronous motor control systems using a highfrequency injection technique[J]. IET Electric Power Applications, 2012, 6(8): 533-544.
[6] 刘颖, 周波, 冯瑛, 等. 永磁同步电机低速无传感器控制及位置估计误差补偿[J]. 电工技术学报,2013, 27(11): 38-45.
Liu Ying, Zhou Bo, Feng Ying, et al. A novel sensorless control method of SPMSM at low speed and estimated rotor position error compensation[J].Transactions of China Electrotechnical Society, 2013,27(11): 38-45.
[7] Reigosa David Díaz, GARCÍA Pablo,Briz Fernando,et al. Modeling and adaptive decoupling of highfrequency resistance and temperature effects in carrierbased sensorless control of PM synchronous machines[J]. IEEE Transactions on Industry Applications, 2010,46(1): 139-149.
[8] Zhu Z Q, Li Y, Howe D, et al. Compensation for rotor position estimation error due to cross-coupling magnetic saturation in signal injection based sensorless control of PM brushless AC motors[C]. IEEE Electric Machines& Drives Conference, 2007: 208-213.
[9] Piippo Antti, Hinkkanen Marko, Luomi Jorma. Sensorless control of PMSM drives using a combination of voltage model and HF signal injection[C]. IEEE Industry Applications Conference, 2004: 964-970.
[10] Jianmin Wang, Jianwei Gao. Analysis of position estimation error resulted from filter in carrier signal injection based sensorless control of PMSM[C]. IEEE Electrical Machines and Systems, 2011: 1-6.
[11] Liu Jiaxi, Ma Mingna, Li Liyi. A position error compensation way for sensorless linear motor drive using high frequency injection[C]. IEEE International Symposium on Electromagnetic Launch Technology,2012: 1-6.
[12] 张剑, 许镇琳, 温旭辉. 新型无位置传感器永磁同步电动机状态估计及其误差补偿方法研究[J]. 电工技术学报, 2006, 21(1): 7-11.
Zhang Jian, Xu Zhenlin, Wen Xuhui. Study of a novel method of state-estimation and compensation for sensorless PMSM drive system[J]. Transactions of China Electrotechnical Society, 2006, 21(1): 7-11.
[13] 尚喆, 赵荣祥, 窦汝振. 基于自适应滑模观测器的永磁同步电机无位置传感器控制研究[J]. 中国电机工程学报, 2007, 27(3): 23-27.
Shang Zhe, Zhao Rongxiang, Dou Ruzhen. Research on sensorless control method of PMSM based on an adaptive sliding mode observer[J]. Proceedings of the CSEE, 2007, 27(3): 23-27.
[14] Foo Gilbert, Rahman M F. Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection[J]. IEEE Transactions on Industrial Electronics, 2010,57(4): 1270-1278.
[15] Accetta Angelo, Cirrincione Maurizio, Pucci Marcello,et al. Sensorless control of PMSM fractional horsepower drives by signal injection and neural adaptiveband filtering[C]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1355-1366.
[16] Repecho V, Biel D, Arias A. Enhanced high frequency injection algorithm for sensorless sliding mode control PMSM drives[C]. IEEE Multi-Conference on Systems, Signals & Devices (SSD), 2014: 1-6.

