复杂海况下飞行器掠海飞行击水概率的模拟研究

关皓，梅华，闻斌，王东良

（北京市5111信箱，北京 100094）

1 引言

无人机、反舰导弹、海上巡航导弹等海上飞行器采用掠海飞行战术能够有效地避开舰载和机载雷达，从而大大增强其生存和突防能力。然而，随着飞行高度的降低，飞行器受海面水文气象条件的影响增大，无人机或导弹的使用条件、运动和受力状态等都受到直接影响。海浪和阵风是影响飞行器掠海飞行的主要环境因素，尤其是海浪，它通过干扰飞行器的飞行高度控制而影响其生存能力，降低其作战效能。

导弹在飞行过程中，通过雷达高度表来测量导弹距海面的高度，与预定高度进行比较，再根据高度控制方程进行控制。当海面存在波动时，雷达高度表的测量高度会发生变化,从而影响对导弹高度的控制，当导弹进行超低空掠海飞行时，海浪造成的高度测定误差，给导弹造成不利影响，甚至使其坠海[1]。飞行器在掠海飞行时受到下垫面海况影响，撞击海浪的概率称为击水概率，它是影响海上飞行器生存能力的重要指标之一。因此有必要对真实海况下，掠海飞行导弹击水概率分布特征进行研究。本文首先对飞行器掠海飞行击水概率的相关算法进行总结分析，然后选择南海海区进行模拟试验，对影响海区的两类典型天气过程中海浪分布进行模拟检验，最后采用解析法模型，定量计算并分析真实海况下某种巡航导弹击水概率的空间分布特征。

2 飞行器击水概率的相关算法

前人就海浪要素对掠海飞行器击水概率的影响做了很多工作。雷小龙等[2]将海浪作为干扰信号对掠海导弹的击水概率问题进行了研究，提出了用均匀设计、蒙特卡洛方法和逐步回归法建立击水概率预报公式的仿真方法，并建立了某型号反舰导弹掠海飞行碰海预测模型。朱璘等[3]在掠海飞行反舰导弹攻击效果的仿真研究中，采用类似方法得到的函数多项式拟合模型计算了某种反舰导弹的击水概率，取得了较好的效果。李一龙等[4]在研究掠海飞行高度对反舰导弹突防能力的影响中，也采用相同方法计算了反舰导弹的生存概率，并给出了反舰导弹采用不同掠海飞行高度在三种海况下的突防概率。

潘幸华等[5]研究了无人飞行器超低空飞行撞地概率问题，建立了地形干扰的数学模型，将撞地事件出现概率当做经典的“零穿越”问题，确定了导弹撞击地面障碍物及正常地形概率的计算方法。该算法应用于周韬等[6]的导弹主要参数对撞地概率影响的研究中，并对地形变化引起的撞地概率进行了定量计算。娄联堂[7]等在误差随机过程为平稳正态过程的假设下，研究了无人飞行器撞地概率的计算问题，在已知地形数据的情况下，从理论上推导出无人飞行器只受到垂直干扰时的撞地概率的计算公式，并在仅利用地形特征参数的情况下，得到了较为简洁的计算公式。张金春等[8]分析了海浪扰动引起反舰导弹坠海的原理，建立了海浪和导弹高度控制系统的数学模型，将文献[5]的撞地概率算法用于反舰导弹坠海概率的计算。湛必胜[9]等人根据概率论的中心极限定理，给出了巡航导弹飞行撞地概率的一种简化算法，通过仿真计算得出与碰海概率有关的高度标准差，估算了浪级为中浪状态下，特定航迹高度导弹的击水概率。郑崇伟[10]等基于第三代海浪模式和文献[9]中击水概率的简化算法，开展了飞行器击水概率的预报研究。

秦志强等[11]深入研究了海上阵风、海浪以及巡航导弹垂直平面内飞行和高度控制等数学模型，给出了阵风、海浪的仿真方法，提出巡航导弹海上生存能力的计算方法和计算流程。李妍等[12]在导弹动力学模型中考虑了海浪要素的影响，结合海浪数值模式，通过仿真试验，客观定量的分析了海浪对巡航导弹掠海飞行的影响。

总结以上研究成果，在飞行器掠海飞行击水概率的分析计算中，可以采用两种方法。（1）仿真法：基于蒙特卡洛方法，在导弹动力学模型中引入波浪等环境要素的影响，对导弹飞行过程进行仿真，通过统计分析可以得到击水概率计算公式；（2）解析法：根据海浪扰动引起飞行器坠海的原理，将地形或波浪扰动作为误差随机过程处理，基于多种假设，得到飞行器击水概率近似计算公式。使用解析法计算击水概率，各种因素对击水概率的影响较直观，便于分析计算，但由于该法采用诸多假设，其计算结果精度不高。采用仿真方法，可以更精确的分析飞行器在各种起始偏差干扰和随机干扰下的飞行性能，但仿真过程加入了特定飞行器参数，通过统计得到的击水概率具有一定的局限性。下面分别列举两种方法得到的飞行器击水（撞地）概率计算公式。

文献[3]基于仿真结果进行统计，利用函数多项式拟合得到掠海飞行反舰导弹击水概率估算公式：

式中，hs为有效波高；L为导弹水平飞行距离；h为导弹飞行高度；β为导弹飞行速度方向与海浪传播方向之间的夹角。

采用解析方法，首先假设导弹飞行离下垫面高度偏差过程：

式中，H0为规划高度；H(t)实际飞行高度，当e(t)＜0 且 e′(t)＞0 时，认为飞行器撞地，且为正穿越。假设误差随机过程e(t)是均值为0，方差为σ2的平稳正态随机过程，自相关系数R(t)，R(0)=σ2。可以得到在已知地形特征，且不考虑水平和垂直干扰的飞行器撞地概率计算公式（3），该式反映了撞地概率P与飞行高度h、飞行时间T、地形高度标准差σ0、概率系数c（由飞行器飞行状态及自身参数决定）的函数关系。

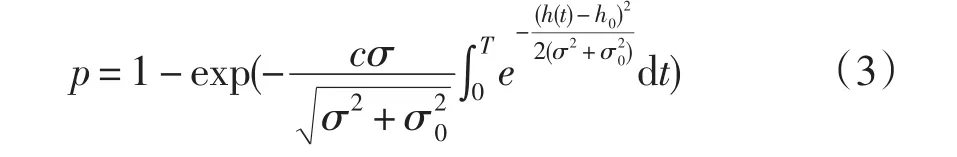
飞行器作低空地形跟踪飞行时，可以积分得到简化公式（4）。飞行器作等高飞行时，可以得到简化公式（5）。上两式被用于实际进行航迹规划或航迹评价中撞地概率计算[7]。

3 海浪数值模拟及检验

南海位于低纬度热带季风区，海区的海气环境复杂多变，热带气旋、冷空气的频繁活动使该海区出现恶劣海况的概率远大于我国近海其它海区。海上大风、巨浪、海雾及强降水等恶劣海况是影响海上活动安全的重要因素。本文选择发生在南海的一次典型的冷空气过程和一次超强台风过程，利用南海中尺度海气耦合模式进行模拟分析，重点检验模式对海上大风，巨浪的模拟效果。

3.1 模式工具

南海中尺度大气-海流-海浪耦合模式是在中尺度大气模式MM5、区域海洋模式POM及第三代海浪模式WAVEWATCHⅢ的基础上建立的，耦合物理方案包括大气动量强迫、海气间热量交换、波浪及海洋飞沫在通量传输中的作用、波致应力对海流的影响以及海表流场对波浪传播的影响。作者前期工作研究了模式对重要海气相互作用过程的敏感性，验证了模式在高海况下对大气、海洋要素的模拟效果[13-14]。

3.2 个例选取

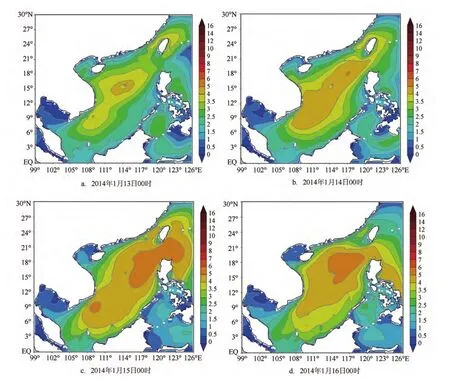
图1 耦合模式模拟的南海海面有效波高分布图（单位：m）

2014年1月中旬，有一次强冷空气过程影响南海北部海区。此次冷空气为典型的东路冷空气，其主体位于乌兰巴托附近，主力指向我国东北-华北地区。13日，冷空气主体东移入海，经南岭回流影响南海东北部海区。试验时段2014年1月9日00时至19日00时（世界时）。

2014年第9号超强台风“威马逊”（Rammasun）于7月12日14时（北京时）在美国关岛以西大约210 km的西北太平洋洋面上生成，16日上午，以台风强度进入南海东部海面，之后稳定地向西北方向移动，18日05时在我国近海加强为超强台风。“威马逊”为近41年来登陆华南、影响南海的最强热带气旋。试验时段2014年7月16日00时至20日18时（世界时）。

3.3 结果及检验

（1）冷空气过程模拟结果及检验

图1为1月13日至16日每日00时（世界时，下同）南海海面有效波高分布图。受冷空气过程影响，14日，南海东北部、中西部出现4 m以上巨浪区，15—16日，受持续偏东风作用，吕宋海峡、南海东北部先后出现5 m以上巨浪区。

采用卫星高度计资料对海浪模拟结果进行检验。高度计资料包括jason-2卫星和saral卫星的沿轨海面风速资料和有效波高资料，海面测高精度2.5—3.4 cm；图2为试验时段内两颗卫星在南海的轨道分布，试验时段分别位于jason-2卫星的cycle203-204和saral卫星的cycle009。从模拟结果对比图（见图3）可以看到，耦合模式较好的模拟了冷空气过程中南海海面风场（图略）和海面有效波高情况：在风速小于15 m/s，波高小于4 m时，模式模拟结果略偏大，在轨道靠近沿岸点，模式模拟有效波高偏小，这主要受高度计资料系统误差、海浪模式地形分辨率及网格插值影响。进一步计算风速和有效波高的模拟误差得到：模式模拟海面风速均方根误差1.412 m，与轨道卫星风速相关系数0.876；海面有效波高均方根误差0.541 m，与轨道卫星波高相关系数0.869。

（2）台风过程模拟结果及检验

图4给出了模式对1409号超强台风移动路径和强度的模拟结果。耦合模式较好地模拟了此次台风在南海的活动过程，台风路径模拟与实况较接近；从对台风强度的模拟来看，耦合模式模拟台风略偏弱，尤其在台风发展较强的时次。这一结论与以往研究[14]中耦合模式对南海西行路径台风的模拟情况一致，考虑与大气模式分量中参数化方案的参数设置和耦合模式中海洋热通量交换偏小有关，具体原因还需要通过敏感性试验进一步研究。

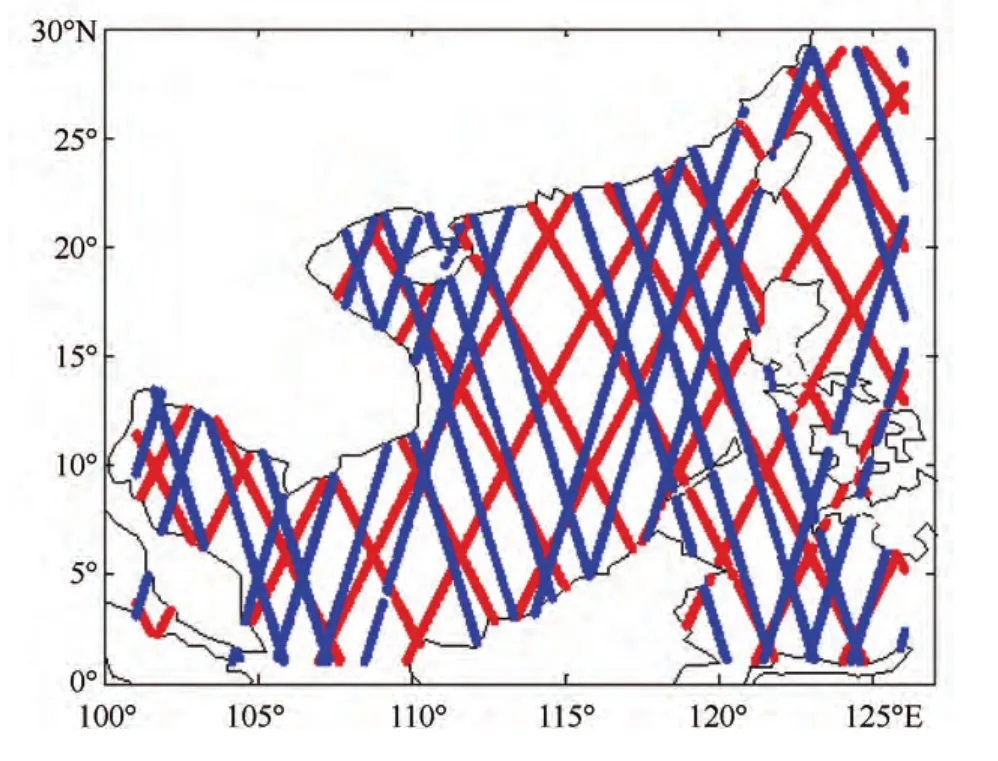
图2 2014年1月9日00时—19日00时卫星轨道分布（红色为jason-2星，蓝色为saral星）

图3 海面有效波高模拟结果对比图（2014年1月9日00时—19日00时）

图4 1409号超强台风移动路径、强度模拟结果与实况对比图

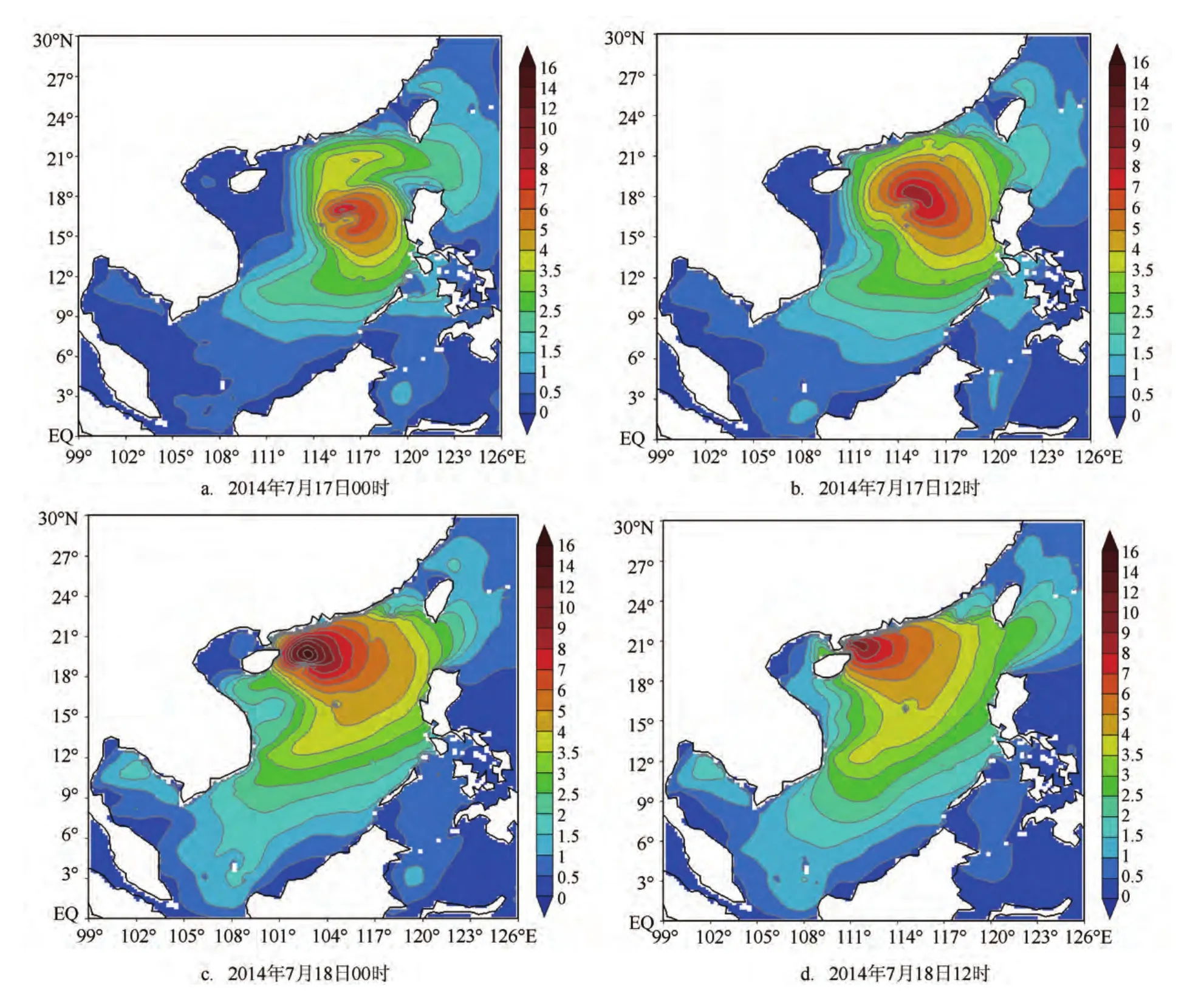
图5 耦合模式模拟的南海海面有效波高分布图（单位：m）

图5给出了1409号台风过程中南海海面有效波高的分布和演变情况。南海海浪场对台风的响应迅速，海浪高值区随台风中心移动，最大波高出现在台风路径右侧危险半圆内，最大台风浪高达到13.8 m。采用卫星高度计资料对海浪模拟结果进行检验。图6为试验时段内两颗卫星在南海的轨道分布，试验时段分别位于jason-2的cycle222和saral的cycle014-015。分析模拟结果对比图（见图7）可以得到，不同轨道上风速和波高的模拟误差差别明显，高海况条件下模拟误差增大。进一步计算风速和有效波高的模拟误差：在此次台风过程中，模式模拟海面风速均方根误差1.975 m，与轨道卫星风速相关系数0.799；海面有效波高均方根误差0.623 m，与轨道卫星波高相关系数0.821。

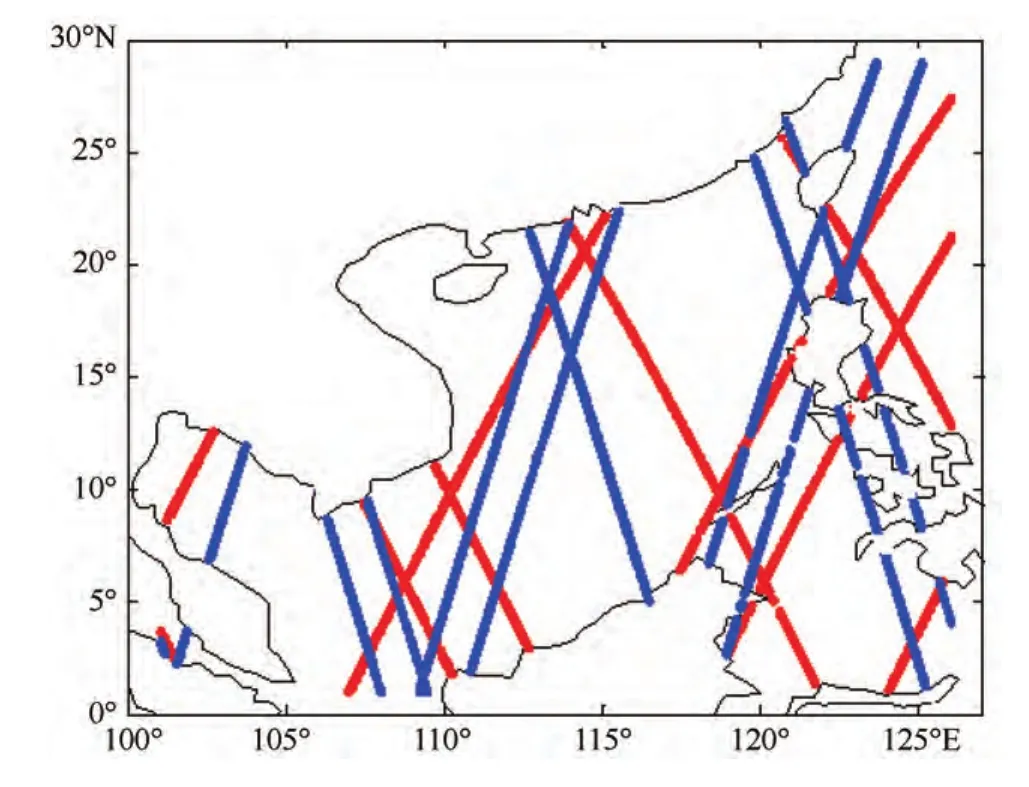
图6 2014年7月16日00时—20日18时卫星轨道分布（红色jason-2星，蓝色saral星）

4 击水概率计算分析

下面采用公式（5）计算两次天气过程中，真实海况影响下某型号巡航导弹的击水概率分布。研究表明[8]，当海浪高度标准差在1.5 m以下时,弹上雷达高度表测量误差非常小，导弹巡航飞行基本上不受海浪影响。因此，只计算波高大于1.5 m的海区导弹巡航飞行的击水概率。巡航导弹掠海飞行高度通常在7—15 m，图8给出了两次典型天气过程中导弹飞行高度为10 m的击水概率分布。分析得到：飞行器击水概率受海面波浪影响显著，击水概率高值区分布与波浪场相对应，在4 m以上的巨浪区，飞行器10 m高度飞行的击水概率超过60%，在高海况下，飞行器击水概率大幅度增加。为了规避恶劣海况下飞行器击水风险，进一步计算了在击水概率小于10%条件下飞行器的最低飞行高度（见图9），在南海4 m以上的巨浪区，为降低击水风险，最低飞行高度应超过13 m，在飞行高度固定的情况下，为降低风险则需要调整飞行线路，以上结论可以为飞行线路调整提供参考。

5 主要结论

本文归纳总结了海浪影响下飞行器掠海飞行击水概率算法研究进展；利用区域海气耦合模式分别模拟了影响南海海区的一次典型冷空气过程和一次超强台风过程，重点检验了模式对高海况下海面风、海浪场的模拟效果；并在其基础上采用解析模型，定量分析了真实海况下某种巡航导弹击水概率的分布特征。得到以下结论：

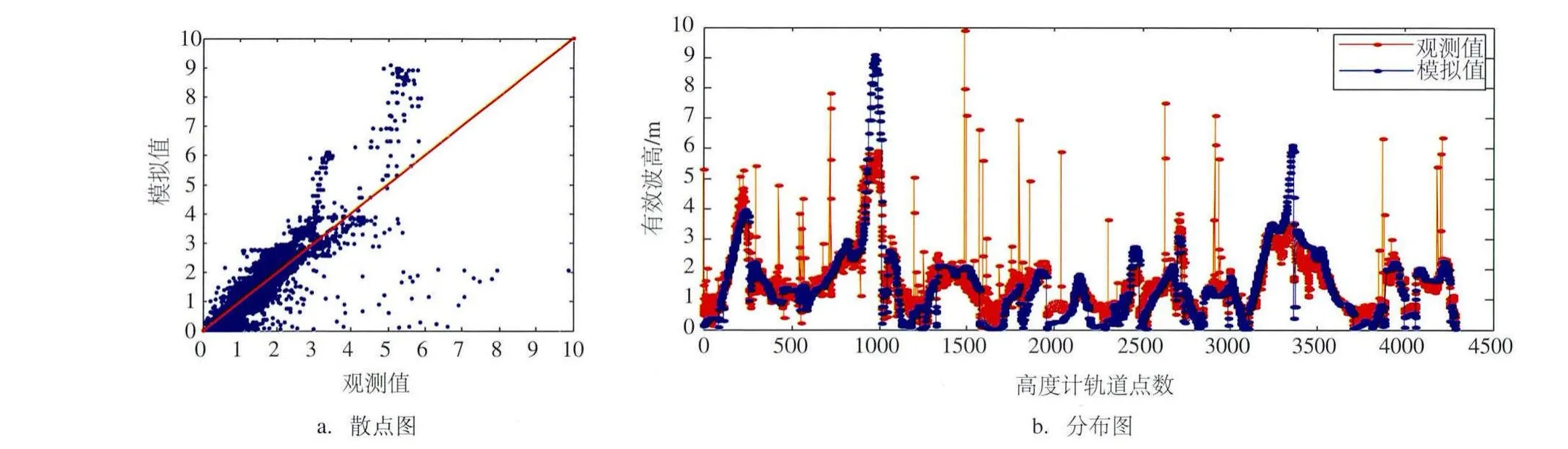
图7 海面有效波高模拟结果对比图（2014年7月16日00时—20日18时）

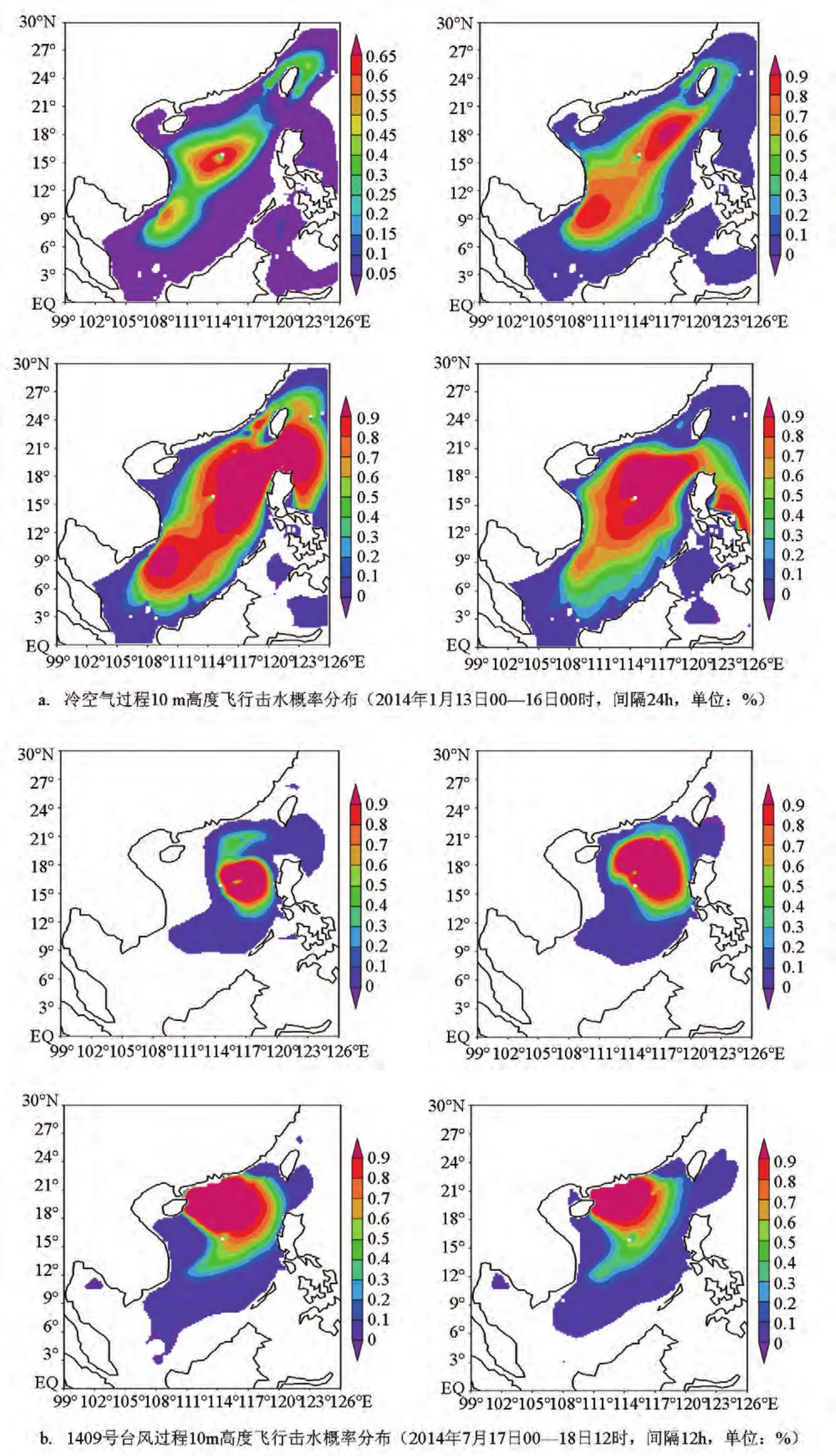
图8 飞行高度为10 m的击水概率分布

图9 飞行击水概率小于10%条件下的飞行高度分布

（1）考虑波浪影响，计算飞行器掠海飞行击水概率可以采用两种方法。解析法直观简便，但计算精度不高；仿真法计算精确，但过程复杂，对特定飞行器具有局限性；

（2）本文采用的耦合模式较好地模拟了冷空气和超强台风过程中南海海浪场的分布和演变特征，采用卫星高度计资料进行检验，模拟有效波高平均均方根误差0.582 m，相关系数0.845；

（3）飞行器击水概率受海面波浪影响显著，在高海况下，飞行器击水概率大幅度增加，其分布与有效波高分布较一致。对于本文研究的特定飞行器，在4 m以上的巨浪区，飞行器10 m高度飞行的击水概率超过60%，为了规避飞行器击水风险，飞行最低高度应在13 m以上；

（4）本文只考虑了波浪对飞行器击水概率的影响，在实际飞行规划和控制中还应考虑其它气象条件、环境因素、仪器误差等对飞行器生存能力和作战性能的影响，还需借助仿真方法对特定飞行器开展研究。

[1]刘剑威,吴传利,徐国亮.反舰导弹典型攻击模式及运动仿真研究[J].指挥控制与仿真,2006,28(5):47-50.

[2]雷小龙,关世义,常伯浚.掠海飞行导弹击水概率的仿真研究[J].宇航学报,1990,(3):16-22.

[3]朱璘,王航宇.掠海飞行反舰导弹攻击效果仿真研究[J].微计算机信息,2008,24(10):15-20.

[4]李一龙,王光辉,吕超.掠海飞行高度对反舰导弹突防能力的影响[J].四川兵工学报,2014,35(1):45-48.

[5]潘幸华,周慧钟,赵靖敏,等.无人飞行器超低空飞行撞地概率初探[J].飞航导弹,1995,(11):28-32.

[6]周韬,周慧钟.导弹主要参数对撞地概率的影响研究[J].北京航空航天大学学报,2008,24(2):240-243.

[7]娄联堂,周成平,丁明跃,等.基于误差随机过程无人飞行器的撞地概率计算公式[J].宇航学报,2003,24(2):121-129.

[8]张金春,叶振北.海浪引起的反舰导弹坠海概率分析[J].战术导弹技术,2010,13(6):29-32.

[9]湛必胜,王明海,李邦杰,等.巡航导弹飞行撞地概率的一种计算方法[J].飞行力学,2006,24(3):78-84.

[10]郑崇伟,潘静,黄刚.利用WW3模式实现中国海击水概率数值预报[J].北京航空航天大学学报,2014,40(3):314-319.

[11]秦志强,王明海,湛必胜.巡航导弹海上生存能力模型研究[J].弹箭与制导学报,2006,26(3):71-73.

[12]李妍,陈希,费树岷.海浪对巡航导弹掠海飞行气动性能的影响[J].弹箭与制导学报,2014,34(3):129-135.

[13]关皓,周林,薛彦广,等.南海中尺度大气-海流-海浪耦合模式的建立及应用[J].热带气象学报,2012,28(2):211-218.

[14]关皓,王汉杰,周林,等.南海台风与上层海洋相互作用的数值模拟研究[J].地球物理学报,2011,54(5):1141-1149.