全球海洋模式中不同海表热力与动力强迫对海温模拟的影响

史珍,李响,凌铁军,刘娜

（1.北京大学物理学院，北京 100871；2.国家海洋环境预报中心国家海洋局海洋灾害预报技术研究重点实验室，北京 100081）

1 引言

海洋是全球气候系统的重要组成部分，以其巨大的储存和释放热量的能力，给气候系统以长期记忆并能影响到从季节到世纪尺度的气候变化。同时，海洋作为全球CO2的汇，存储了约93%的CO2，是大气的50倍，陆地生态系统的20倍[1]。基于海洋的重要性，越来越多的学者关注海洋的研究。但由于海洋的观测比较困难，海洋数据较少且在时间和空间上分布不均，绝大部分海洋数据位于北半球及其海表面附近，同时海洋数据一般为间接获得，通常只提供热力场而缺少速度场。因此，目前进行海洋研究及预测的最主要工具是海洋环流模式，其不仅可以模拟及预测海洋环流状况，同时可以用于研究海洋生物地球化学[2]。

自20世纪60年代普林斯顿大学的地球物理流体动力学实验室（GFDL）研究开发了第一个海洋普通环流模式开始，至今各科研机构已发展40多个海洋模式[3]。这些模式具有各自不同的特点，分别适用于不同海域和不同海洋学科方向。目前国内外常用的业务化海洋模式有HYCOM、NEMO、MOM、ROMS和POM等，其中HYCOM、NEMO及MOM模式为全球海洋环流模式。在假定潮汐力对海洋长期平均性质的影响可以忽略的情况下，海洋模式主要是由风应力、热通量及淡水通量三种“外力”驱动[4]。采用不同的外强迫场时，海洋会产生不同的响应，因此采用何种外强迫场会对海洋模式的模拟及预报结果产生直接的影响。

国际上常用的用于驱动海洋模式的强迫场数据集有多种，包括：美国国家环境预报中心（NCEP）的再分析数据集（R2）[5]、欧洲中期数值预报中心（ECMWF）的三代再分析数据集（ERA-15、ERA-40以及ERA-Interim）[6]、日本气象厅（JMA）的25年再分析数据集（JRA-25）[7]、美国NCEP的气候预报系统再分析数据集（CFSR）[8]、美国航空航天局（NASA）的再分析数据集（MERRA）[9]、以及美国国家气候数据中心的海洋大气综合数据集（COADS）[10]等。这些数据集各自具有不同的特点，国内外学者对这些数据集进行了一定的对比研究。张增海[11]对比了六套数据在南海区域的感热通量及潜热通量，结果表明HOAPS2（Hamburg Ocean-Atmosphere ParametersandFluxesfromSatelliteData2）、NCEP1,2以及ERA40数据均或多或少的高估了该区域的热通量值。Josey等[12]对比了5套数据的风应力，发现NCEP的风应力偏弱，而Hellerman and Rosenstein（HR）数据的风应力偏强，ERA40、COADS数据则与南安普顿国家海洋学中心（Southampton Oceanography Centre，SOC）数据的结果有较好的一致性。Brunke等[13]评估了6套再分析数据的潜热、感热以及风应力的不确定性，研究了各个变量的误差范围，其中潜热为3.0—20.2W·m-2、感热为1.4—6.0 W·m-2、风 应 力 为 7.6×10-3— 7.9×10-3N·m-2。Chaudhuri等[14]研究了常用于海洋模式外强迫的大气再分析产品的不确定性，结果表明ERA-Interim，CORE2（Coordinated Ocean-ice Reference Experiments V2），JRA-25以及NCEP 4套再分析产品尽管具有一定的可比性，但是没有一套数据参与评估的8个变量与卫星数据完全相符。国内外的研究人员不仅对这些常用的大气分析场进行对比，更进一步的对比研究了不同的外强迫数据集对海洋模式模拟结果的影响。俞永强等[15]采用3种不同的风应力数据强迫中国科学院大气物理研究所大气科学和地球流体力学数值模拟国家重点实验室的全球海洋环流模式（IAP/LASG Climate System Ocean Model，LICOM），结果表明3个试验的结果大致相同，但也体现了不同的特征，ERA和佛罗里达州立大学“伪”风应力（FSU）试验模拟的SST距平的强度要好于NCEP再分析数据（NCEP Reanalysis，NRA）试验，但是NRA试验模拟的位相比另外两个试验更合理。Hunke等[16]使用三套数据分别强迫一个全球海洋海冰耦合模式，发现尽管外强迫场差异较小，但是模拟结果却产生了较大的差异。陈光泽等[17]用数值模拟研究了海表流场对外强迫（风应力和海表热通量）的响应特征，结果表明不同海区的表层环流对这些外强迫有不同的响应特征。俞永强等[18]对比3套不同来源的海表热通量和风应力资料在热带太平洋和印度洋区域的差异，并强迫一个海洋模式研究了印度洋和西太平洋暖池对这些外强迫响应的敏感性。虎雅琼等[19]用3套外强迫数据驱动LICOM模式，设计了多组试验研究不同的外强迫场对模拟结果的影响，发现海洋模式对比计划的（Ocean Model Intercomparisin Project，OMIP）风应力数据和NCEP的SST数据更适合作为LICOM模式的强迫场。以上这些研究中均未探讨过CFSR数据集强迫全球海洋模式对模拟结果的影响。

目前，国内外海洋预报蓬勃发展，主要海洋大国均建立了先进的海洋预报系统[20]。国家海洋环境预报中心采用MOM4模式进行未来5 d的全球海洋预报，其动力及热力强迫场采用NCEP的全球预报系统（Global Forcast System，GFS）数据。由于GFS数据的预报时效仅为15 d，该强迫数据无法用于气候预测中。CFSR数据作为国际上比较新的高分辨率数据，在预报中心大气的短期气候预测中使用。本文着眼于业务的短期海洋气候预测，对比研究了CFSR数据集与NCEP数据集的差异，并考察这两种不同的外强迫数据对MOM4模式的模拟结果的影响，为未来建立用于业务的全球海洋预测系统提供理论及试验支持。

2 模式及数据介绍

2.1 模式介绍

MOM4模式[21]是由GFDL开发的模块化海洋模式。该模式为自由表面原始方程海洋模式，采用非Boussinesq近似和静力近似，垂直坐标采用z坐标系，水平网格采用Arakawa B网格。模式提供了多种垂直混合参数化方案，包括KPP方案、Richardson数决定的涡动混合系数法等。该模式主要用于海洋气候系统研究和海洋预报。

本文的MOM4模式计算范围88.75°S—90°N,包含了全球所有大洋，水平网格分辨率为1/4°×1/4°，最大水深取为5500 m，垂向分为50层。模式中采用OCCAM 0.2°资料作为海底地形。通过提高MOM4在接近海表面处网格垂向分辨率，使上温跃层有更好的模拟效果。较高的水平分辨率提高了对副热带和极地海域的海洋环流结构及温度盐度等海洋环境要素的模拟能力。为了方便对北极点的处理，水平网格设计时采取三极点网格，可以有效消除北极奇点。全球海洋模式不需人为给定任何侧边界及开边界条件，温、盐、流等要素都是由模式本身直接模拟得到的，摒弃了以往一般区域模式开边界选取的人为性，将有利于提高全球及重点关心海域海洋要素的模拟精度。模式积分时间步长取值为：温、盐积分步长及流速时间步长和自由表面积分步长均取为1500 s，流函数积分时间步长取为25 s。模式采用来自OMIP_NCAR气候态数据集的海平面气压，10 m温度、比湿、风速、降水、长波辐射、短波辐射等数据作为外强迫场，运行气候态积分20 a。高频大气强迫数据分别采用CFSR月平均数据集及NCEP月平均数据集。所有资料均经过插值以适应模式需要。

2.2 试验设计及数据介绍

为了考察不同空间分辨率的外强迫数据集对MOM4模式的模拟结果的影响，本文设计了两组试验，分别为：采用CFSR数据集作为外强迫的试验，记作CFSR；以及以NCEP-DOE R2数据集作为外强迫的试验，记作NCEP。

本研究中用到的数据包括如下：

（1）美国国家环境预报中心（NCEP）的气候预测系统再分析数据（CFSR），该数据为1981年1月—2008年12月的月平均数据，水平分辨率为0.5°。该数据作为CFSR试验的外强迫数据驱动MOM4模式；

（2）美国国家环境预报中心（NCEP）再分析数据2（NCEP-DOE R2），该再分析数据是在NCEP/NCAR再分析数据1基础上改进而来。该数据为1981年1月—2008年12月的月平均数据，高斯网格，水平分辨率约为2°。该数据作为NCEP试验的外强迫数据驱动MOM4模式；

（3）美国马里兰大学的海洋再分析数据（SODA）[22-23]，该数据为1981年1月—2008年12月的月平均数据，水平分辨率为0.5°，垂直共40层。该数据作为观测数据与两组实验数据进行对比。

3 不同海表动力及热力强迫场的对比

为了更好的理解不同动力强迫场及热力强迫场对MOM4模拟结果的影响，首先对这两组不同的动力及热力强迫场进行对比分析。

3.1 动力强迫场的对比

海表面风场通过向海洋表层释放动量驱动海洋，在这个过程中最重要的大气参量就是风应力。风应力是驱动海洋上层环流的直接动力，是决定上层海水流动和影响SST分布的重要外部动力。图1给出了两套数据1月份及7月份的风应力平均值和1月份及7月份两套数据相对于平均风应力的差值。不论是1月还是7月，两套数据中风应力的大尺度空间分布基本一致，其主要特征在1月份表现为：在35°N以北的太平洋中高纬度主要被大范围的气旋性环流控制，大西洋则盛行西南风；在北印度洋大范围的东北季风跨越赤道后在10°S左右与南印度洋低纬的东南信风交汇，形成弱风槽，而西北太平洋则受到东北季风的影响，北半球低纬度其他海区盛行东北信风，并跨赤道与南半球地位东南信风交汇；南半球中高纬盛行西风。两套数据的风应力在1月份的差异主要表现为：除了赤道太平洋海域外，其他海域中CFSR数据的风应力偏强，而NCEP数据的风应力偏弱。7月份两套数据的平均风应力类似于1月份的情况。其他月份的结果与此类似（图略）。造成两套数据风应力差别的原因很多，如观测数据来源不一致、风应力计算方案的差异、模式及同化方案的差别等。

3.2 热力强迫场的对比

净的海表热通量，它是由净的短波辐射通量，净的长波辐射通量，潜热通量以及感热通量4部分组成。海表的净热通量对SST的模拟具有非常重要的影响。图2给出了两套数据1月份及7月份的海表净热通量平均值和1月份及7月份两套数据相对于平均海表净热通量的差值。从图中可以看出，两套数据的净热通量的空间分布类似，1月份海洋的净热通量南半球为正，海洋净吸收热量，而北半球除了赤道东太平洋及赤道西大西洋区域外，其他海域均为负的净热通量，海洋向外放出热量，其中在黑潮区域存在负的净热通量大值区。两套数据1月份平均的净热通量的差异为CFSR数据在绝大部分的太平洋海域释放更少的热量或吸收更多的热量（图2c），而NCEP数据在印度洋及绝大部分的大西洋海域释放更少的热量或吸收更多的热量（图2e）。7月份的结果（图2b、d、f）以及其他月份（图略）的结果类似于一月份。

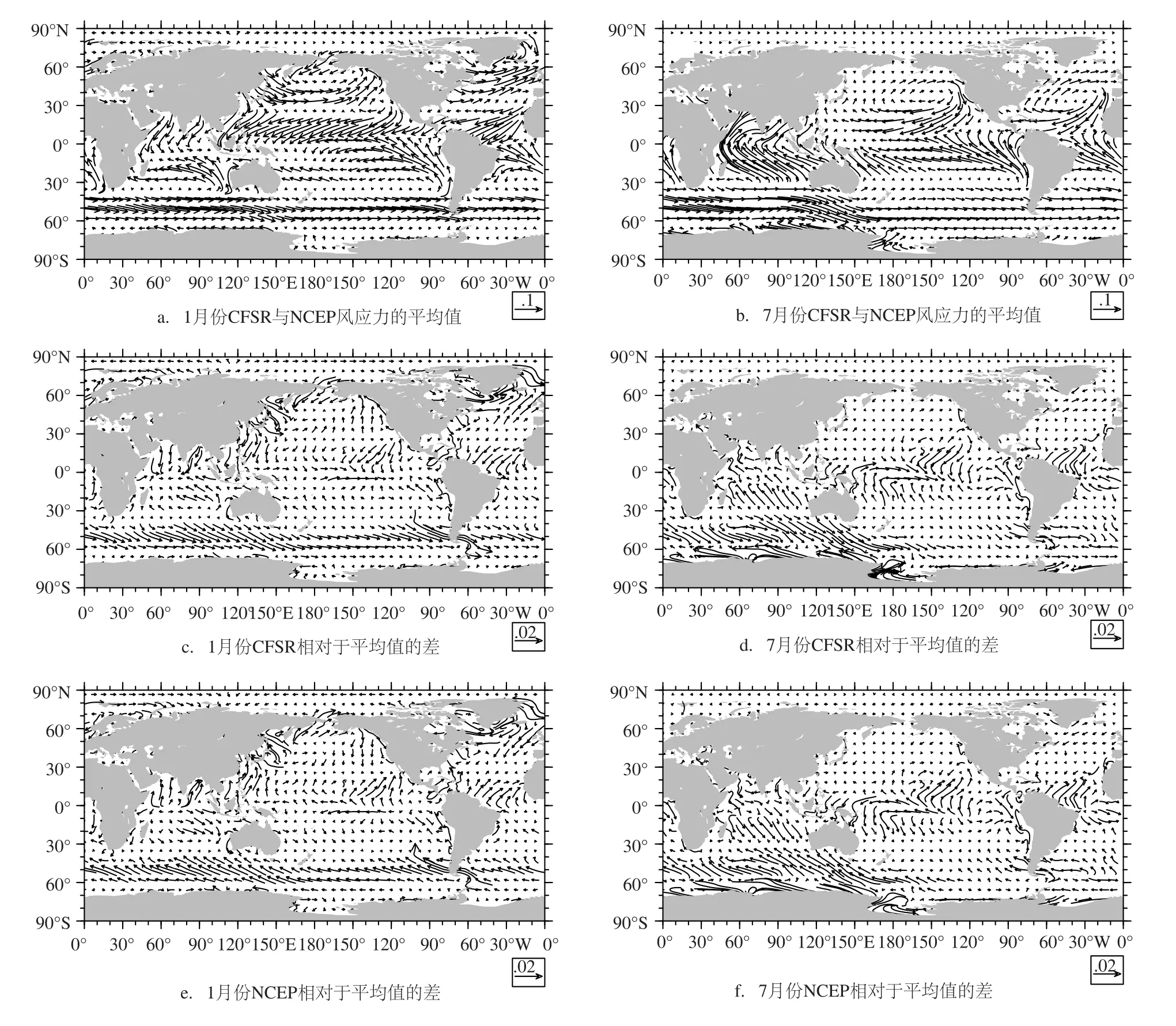
图1 全球风应力图（单位：N·m-2）

4 模拟结果对比分析

4.1 海表温度的气候态

SST在很大程度上控制着海洋向大气输送水分的空间分布和强度，它本身又受到海气相互作用的强烈影响，因而成为联结大气和海洋的最重要的变量。对于气候模式来说，SST是检验海洋模式能力的第一指标。

图3给出了采用不同外强迫的MOM4模拟的28 a平均SST全球空间分布和1981—2008年共计28 a SODA的年平均SST。从图中可以看出，两种外强迫数据均能使得MOM4模式再现全球SST的整体分布特征。SST等值线在中高纬度基本上都是沿着纬向分布的，等值线在中纬度较为密集，尤其是在大西洋及太平洋的西海岸的海域最为明显，体现了西边界流的特征。SST沿纬向不对称分布则主要集中在赤道附近的热带大洋上，尤其是热带太平洋海域，其东部偏暖而西部偏冷。在赤道偏北区域存在一暖水区，而赤道东太平冷海水区域与东南太平洋相连，形成冷舌。

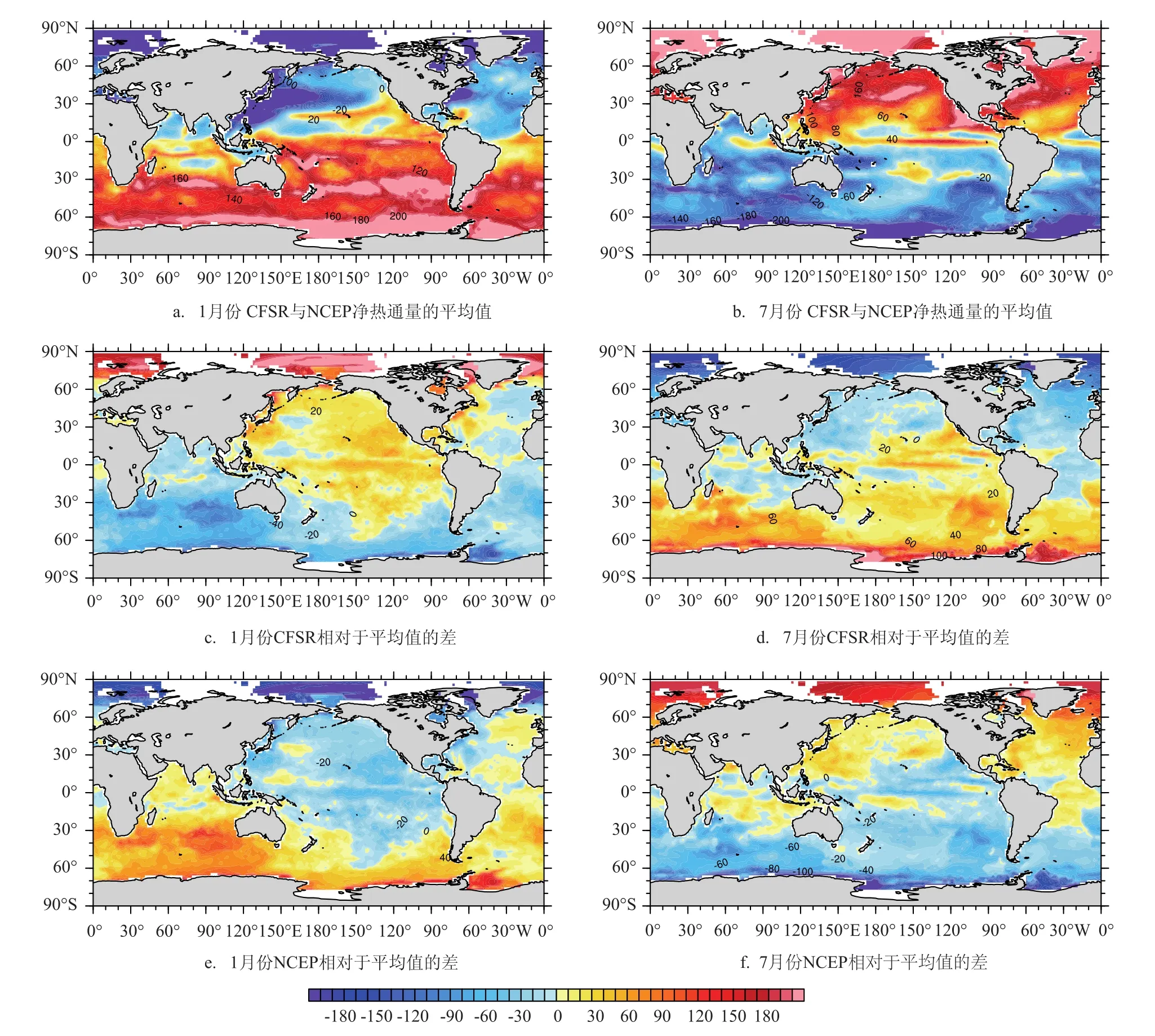
图2 全球净热通量图（单位：W·m-2）

虽然两套外强迫数据均能使MOM4模式模拟出SST的全球平均分布形态，但是模拟结果与观测之间仍然存在一定的差异。如图3d所示，CFSR试验中，其模拟的年平均海温在太平洋海域偏暖，整个洋盆偏暖约1—3℃，其中最大偏差出现在南太平洋海域，偏暖超过3℃。在印度洋海域，模拟的SST偏差较小，绝对值均在1℃以内，其中北印度洋及南印度洋海温偏冷，而赤道中印度洋海域偏暖。大西洋呈现SST偏冷偏热交替出现的情况。NCEP试验中，除了赤道东太平洋及赤道大西洋区域外，其他海域均表现为SST偏暖。但是与CFSR试验相比较，NCEP试验在太平洋的SST偏差较小，而印度洋及大西洋区域的SST偏差相对较大。这与净热通量的差异分布较为一致，更多的加热导致SST的偏差也较大。

4.2 海温的垂直分布

图3 全球28 a平均海洋表面温度图（单位：℃）

图4给出了观测及两组模拟试验的全球纬向平均的海温的纬度-深度分布图。从图中可以看出，两组试验模拟的纬向平均海温随的纬度-深度分布与SODA数据的结果具有较为一致的模态。比较有代表性的4℃等温线均位于水深1000 m附近，且在30°S附近向下伸展至2000 m左右。但是在赤道附近的浅层海洋，两组模拟试验的海温的垂直分布与观测有较大的差异，尤其在水深小于50 m海洋中。观测中，在赤道附近存在一个28℃以上的暖水区，且范围在10°S—0°之间，CFSR试验的模拟结果在赤道两侧分别有一个暖水区，且范围较大，位于10°N—15°S之间，而NCEP试验的模拟结果在赤道温度略低，而在赤道南北两侧分别有一个暖水区，分别位于10°—5°N之间以及12°S—0°之间。NCEP数据的风应力在0°—15°S的风应力偏大，使得垂直混合加强，导致海温相对CFSR试验偏低。由于CFSR试验在赤道附近吸收更多的热量，尽管在其他区域CFSR的风应力偏大，加强的垂直混合导致的直接结果是高海温区域延伸到海洋的更深处。

4.3 海温的季节变化

图4 全球纬圈平均的海温随纬度和深度分布图（单位：℃）

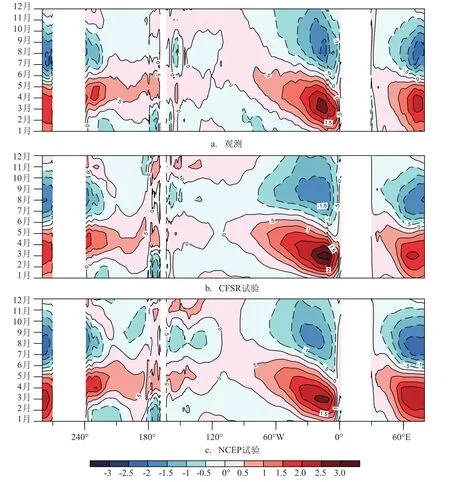
图5 近赤道（2°S—2°N）SST的季节变化图（单位：℃）

图5给出了采用两套不同的外强迫数据对SST季节变化的模拟与观测的对比。在赤道太平洋区域，观测的SST季节变化主要表现为赤道东太平洋为显著的年循环，赤道西太平洋为较弱的半年循环。在赤道大西洋区域及赤道印度洋区域，观测的SST季节变化为显著的年循环特征，但是强度相对赤道东太平洋弱。两组试验均能模拟出观测的SST季节变化特征，总体体现为春季暖异常，秋季冷异常，但同时也存在一定的差异性。在赤道东太平洋区域，相比于观测，CFSR试验模拟的SST的正异常偏强，而负异常偏弱，且正异常中心偏东；NCEP试验模拟的SST正异常偏弱且持续时间较短，而负异常偏弱，且正异常中心偏东。在其它赤道大洋上，相比于观测，CFSR试验模拟的SST的季节异常均偏弱，而NCEP试验模拟的SST的季节异常均偏强。

4.4 海温的年际变化

在年际尺度上，热带太平洋海温年际变化的最主要特征是ENSO，它也是年际时间尺度上气候变量的最主要模态，印度洋海温年际变化的最主要特征是印度洋偶极子(IOD)。这些事件通常可以通过用特定区域的SST异常进行定义。

4.4.1 热带太平洋海温年际变化

热带太平洋海温年际变化的最主要特征是ENSO[24-25]。当ENSO处于正位相时，海洋对应为El Niño事件，表现为赤道中东太平洋大范围持续异常偏暖；与之相反，当ENSO处于负位相时，海洋对应为La Niña事件，表征为赤道中东太平洋大范围持续异常偏冷。通常用赤道东太平洋特定区域海温异常的平均值代表ENSO指数。不同的研究人员对ENSO指数的定义的不同[26]，将赤道东太平洋划分了不同的Nino指数计算区域，这些区域包括Nino1+2区域，Nino3区域，Nino4区域以及Nino3.4区域，对应的Nino指数则为Nino1+2指数，Nino3指数，Nino4指数以及Nino3.4指数。本研究中以Nino3.4指数为代表，研究采用不同外强迫数据强迫MOM4模式，模拟的ENSO的差异。

图6 逐月Nino3.4指数变化图（单位：℃）

图7 逐月DMI指数变化图（单位：℃）

根据Nino3.4指数的定义，分别计算了SODA数据、CFSR试验及NCEP试验的Nino3.4指数，并进行了对比分析。图6给出了逐月Nino3.4指数变化观测值与CFSR试验、NCEP试验的对比。从图中可以看出，CFSR试验及NCEP试验计算得到的Nino3.4指数与SODA数据计算得到的Nino3.4指数具有一致的变化特征。其中，CFSR试验的Nino3.4指数与观测的Nino3.4指数的相关系数达到了0.89；而NCEP试验的Nino3.4指数与观测的Nino3.4指数的相关系数则达到了0.97。两者均超过了99%的信度检验。对于几次强的El Niño事件均模拟的较好，如1982—1983年及1997—1998年，El Niño事件的持续时间及振幅均与观测较为一致。但是对于La Niña事件，在2000年前，CFSR试验模拟的振幅偏大，而在2000年以后，CFSR试验模拟的振幅偏弱。NCEP试验在整个模拟期间，Nino3.4指数均与观测非常一致。这表明在赤道东太平洋区域，采用NCEP数据作为外强迫模拟的海温更接近观测。

4.4.2 印度洋海温的年际变化

在热带印度洋区域，存在着SSTA的偶极子分布特征。Saji等[27]将赤道西印度洋（50°—70°E，10°S—10°N）和东南印度洋（90°—110°E，10°S—0°）海区平均的SSTA之差定义为印度洋偶极子指数（DMI）。当DMI为正值时，偶极子处于正位相时期，印度洋海温异常呈西正东负的模态；与之相反，当DMI为负值时，偶极子处于负位相时期，印度洋海温异常呈西负东正的模态。

根据Saji等人的定义，分别计算了SODA数据、CFSR试验及NCEP试验的DMI指数，并进行了对比分析。图7给出了逐月DMI指数变化观测值与CFSR试验、NCEP试验的对比。从图中可以看出，CFSR试验及NCEP试验计算得到的DMI指数与SODA数据计算得到的DMI指数具有一致的变化特征。对于几次强的IOD正位相年份及负位相年份，均有较好的模拟。其中，CFSR试验的DMI指数与观测的DMI指数的相关系数达到了0.85；NCEP试验的DMI指数与观测的DMI指数的相关系数也达到了0.8。两者均超过了99%的信度检验。但是需要指出的是，在大部分年份中，NCEP试验的DMI指数的振幅相对较大。这表明在印度洋区域，采用CFSR数据作为外强迫模拟的海温更接近观测。

5 结论

本文利用MOM4模式研究了全球海洋模拟对不同的海表动力及热力强迫的响应情况，并与SODA海洋同化数据进行了对比，主要结论如下：

（1）两套数据的风应力及净热通量的对比结果表明，CFSR数据的风应力相对于NCEP数据偏大，而CFSR数据的净热通量相对于NCEP数据偏小；

（2）两套数据强迫MOM4模式能再现SST的总体空间分布特征，但是区域性差异仍然存在，如CFSR试验模拟的海温在印度洋区域误差相对较小，而NCEP试验模拟的海温在太平洋区域误差相对较小，这与两套数据的净热通量的差异分布较为一致；

（3）两组试验模拟的海温的垂直分布结构与观测类似，但是在上层海洋海温的模拟差异较大，尤其是赤道附近，两组试验均表现为两道南北两个暖水区，但是NCEP试验在赤道以南的暖水区相对较小，一方面是由于NCEP数据在该区域的净热通量相对偏小，海温相对偏低，另一方面更强的风应力导致垂直混合加强，降低海温；

（4）对于SST季节循环的模拟，两组试验对海温的季节循环均的周期模拟较好，但是SST异常的大小存在一定的差异，CFSR试验在太平洋区域偏暖更多，而NCEP试验在印度洋及大西洋偏暖更多；

（5）两组试验模拟的海温年际信号均与SODA数据较为一致，其中CFSR试验模拟的DMI指数更加接近观测，而NCEP试验模拟的Nino3.4指数更加接近观测。

[1]胡敦欣.海洋在全球气候变化中的作用——概况、展望与建议[J].科学中国人,2005,11:23-25.

[2]赵琦,陈中笑,徐永福,等.全球海洋CFC-11吸收对传输速度的敏感性[J].大气科学,2012,32(6):1253-1268.

[3]赵艳玲,张铭,司广宇.海洋环流模式研究回顾与展望[J].解放军理工大学学报(自然科学版),2006,7(3):281-290.

[4]张学洪,俞永强,周天军,等.大洋环流和海气相互作用的数值模拟讲义[M].北京:气象出版社,2013.

[5]Kanamitsu M,Ebisuzaki W,Woollen J,et al.NCEP-DOE AMIP-II Reanalysis(R-2)[J].Bulletin of the American Meteorological Society,2002,83(11):1631-1643.

[6]Uppala S M,Kållberg P W,Simmons A J,et al.The ERA-40 re-analysis[J].Quarterly Journal of the Royal Meteorological Society,2005,131(612):2961-3012.

[7]Onogi K,Tsutsui J,Koide H,et al.The JRA-25 Reanalysis[J].Journal of the Meteorological Society of Japan Ser II,2007,85(3):369-432.

[8]Center E M.NCEP Climate Forecast System Reanalysis(CFSR)selected hourly time-series products,January 1979 to December 2010[J].Research Data Archive at the National Center for Atmospheric Research,Computational and Information Systems Laboratory[Available online at http://rda ucar edu/datasets/ds0931]2010.

[9]Rienecker M M,Suarez M J,Gelaro R,et al.MERRA:NASA’s Modern-Era retrospective analysis for research and applications[J].Journal of Climate,2011,24(14):3624-3648.

[10]Slutz R J,Lubker S J,Hiscox J D.COADS:comprehensive ocean-atmosphere data set release 1[M].1985.

[11]张增海.南海湍流热能量的质量分析和季节变化研究[D].青岛:中国海洋大学,2006.

[12]Josey S A,Kent E C,Taylor P K.Wind stress forcing of the ocean in the SOC Climatology:Comparisons with the NCEP-NCAR,ECMWF,UWM/COADS,and hellerman and rosenstein datasets[J].Journal of Physical Oceanography,2002,32(7):1993-2019.

[13]Brunke M A,Wang Z,Zeng X B,et al.An assessment of the uncertainties in ocean surface turbulent fluxes in 11 reanalysis,Satellite-derived,and combined global datasets[J].Journal of Climate,2011,24(21):5469-5493.

[14]Chaudhuri A H,Ponte R M,Forget G,et al.A comparison of atmospheric reanalysis surface products over the ocean and implications for uncertainties in Air-sea boundary forcing[J].Journal of Climate,2013,26(1):153-170.

[15]俞永强,Izard A,张学洪,等.IAP/LASG海洋环流模式对风应力的响应[J].大气科学,2001,25(6):721-739.

[16]Hunke E C,Holland M M.Global atmospheric forcing data for Arctic ice-ocean modeling[J].Journal of Geophysical Research:Oceans,2007,112(C4):C04S14,doi:10.1029/2006JC003640.

[17]陈光泽,张铭,李崇银.表层洋流对外强迫响应敏感度的数值研究[J].大气科学学报,2011,34(2):199-208.

[18]俞永强,李超,王东晓,等.暖池季节变化的数值模拟及其对海表热力和动力强迫的敏感性[J].热带海洋学报,2011,30(1):1-10.

[19]虎雅琼,刘海文,李阳春,等.全球海洋模式对不同强迫场的响应[J].大气科学,2015,39(1):180-196.

[20]方长芳,张翔,尹建平.21世纪初海洋预报系统发展现状和趋势[J].海洋预报,2013,30(4):93-102.

[21]Griffies S M,Harrison M J,Pacanowski RC,et al.A technical guide to MOM4[J].GFDL Ocean Group Tech Rep 2004;5:371.

[22]Carton J A,Chepurin G,Cao X H,et al.A simple ocean data assimilation analysis of the global upper ocean 1950-95.Part I:Methodology[J].Journal of Physical Oceanography,2000,30(2):294-309.

[23]Carton J A,Chepurin G,Cao X H.A simple ocean data assimilation analysis of the global upper ocean 195095.Part II:Results[J].Journal of Physical Oceanography,2000,30(2):311-326.

[24]巢纪平.厄尔尼诺和南方涛动动力学[M].北京:气象出版社,1993.

[25]黄荣辉.ENSO及热带海-气相互作用动力学研究的新进展[J].大气科学,1990,14(2):234-242.

[26]李晓燕,翟盘茂.ENSO事件指数与指标研究[J].气象学报,2000,58(1):102-109.

[27]Saji N H,Goswami B N,Vinayachandran P N,et al.A dipole mode in the tropical Indian Ocean[J].Nature,1999,401(6751):360-363.