Integral型Lupas-Bézier算子收敛阶的估计
黄坤阳
(泉州师范学院数学与计算机科学学院,福建 泉州 362000)
Integral型Lupas-Bézier算子收敛阶的估计
黄坤阳
(泉州师范学院数学与计算机科学学院,福建泉州362000)
运用概率型算子的概率性质,研究了局部有界函数f的Integral型Lupas-Bézier算子收敛阶,得到更精确的估计。其研究对于Bézier型算子逼近的研究工作,以及提高运用Bézier法的计算机辅助设计几何造型的精度的估计有重要意义。
Integral型Lupas-Bézier算子;收敛阶;估计
文献[1-2]主要研究了定义在区间[0,∞)上局部有界函数f的Integral型Lupas-Bézier算子收敛于[f(x+)+α f(x-)]/(α+1)的收敛阶的估计。本文中我们进一步讨论了文献[1-2]关于Integral型Lupas-Bézier算子收敛阶,利用基函数的概率性质等方法,在其基础上给出了更精确的估计式。关于概率型算子逼近理论的相关研究可参见文献[3-7]。首先我们介绍Integral型Lupas-Bézier算子。文中所采用的记号与文献[1]同。
1 定义和引理
定义1设f是定义在区间[0,∞)上的可测函数,称下列为Integral型Lupas-Bézier算子:
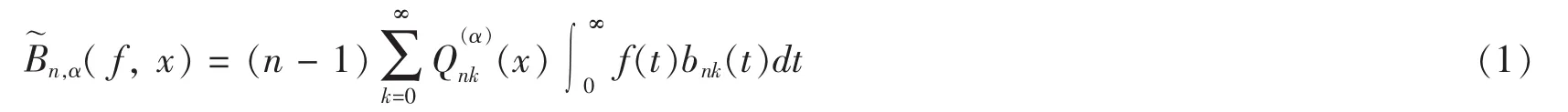

为了得到本文的结果,我们引入一些引理。
引理1[8]设为独立同分布的随机变量序列,数学期望EXi=a1∈(-∞,∞),方差DX1=σ2>0,三阶绝对矩.又设Fn是的分布函数,对于所有的n=1,2,…,则

引理2设X服从分布:P(X=k)=xk(1+x)-1-k(k=0,1,2,…)x∈(0,∞),则X方差σ2及三阶绝对矩ρ分别为
由于0≤Jnk(x),Jn-1,k+1(x)≤1,α≥1.故

证明:求各阶原点矩:

引理3对一切x∈(0,∞)及k=0,1,2,…,有

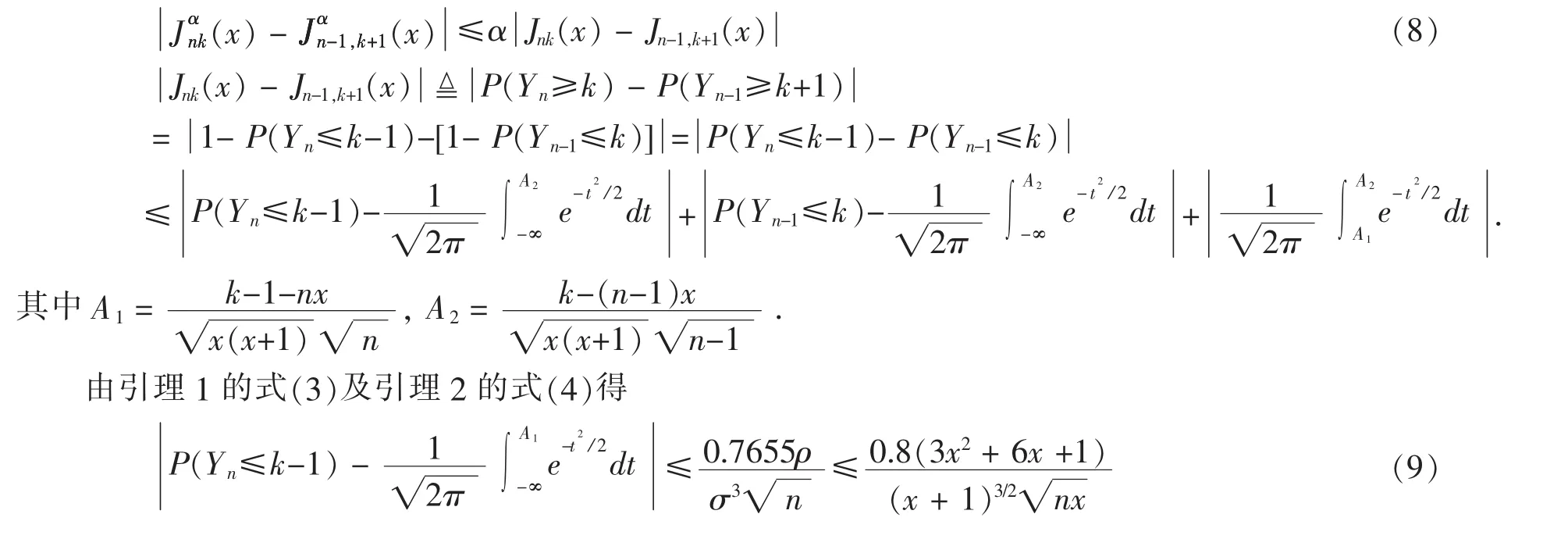
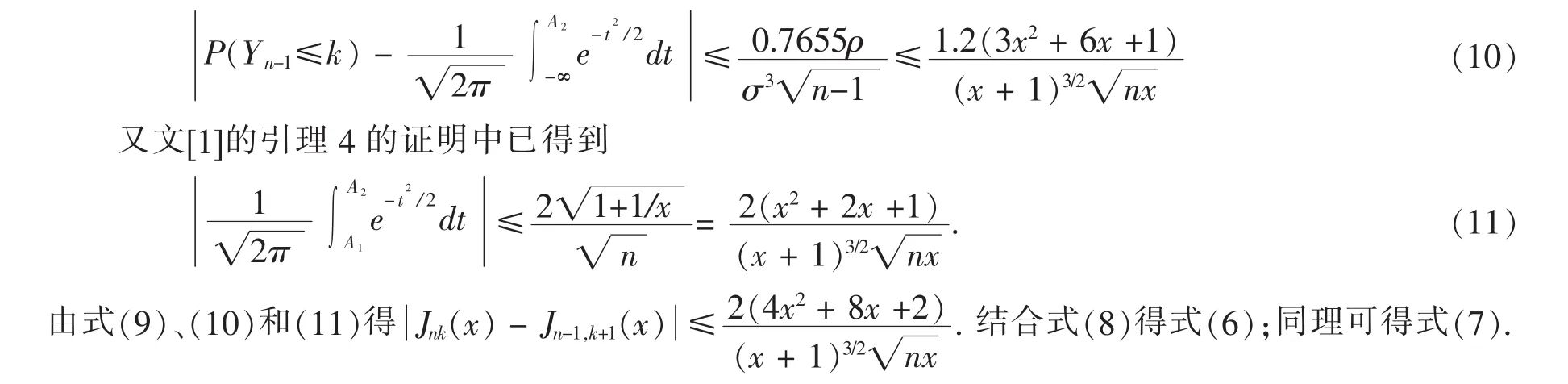
2 主要结果


另一方面,文[2]已给出了的估计式

把式(15)、(18)代入式(14)得式(12),定理1得证。
我们把结果与文献[1]和文献[2]进行比较,可见本文关于局部有界函数f的Integral型Lupas-Bézier算子的收敛阶的估计式更优。
[1]Zeng X.M,Wang T.Rate of convergence of the integral type Lupas-Bezier operators[J].Kyungpook Mathematical Journal. 2003,(4):593-604.
[2]王平华,沈晓斌,李志伟.Integral型Lupas-Bézier算子的收敛阶[J].泉州师范学院学报,2007,(6):1-4.
[3]Gupta V,Pant R.P.Rate of convergence for the modified Szasz-Mirakyan operators on functions of bounded variation[J].J. Math.Anal Appl.,1999,(233):476-483.
[4]Zeng X.M,Gupta V.Rate of Convergence of Baskakov-Bezier Type Operators[J].Computers and Mathematics with Applications,2002,(10-11):1445-1453.
[5]Wang P.H,Cai Q.B,Li Z.W.Estimate on Rate of Convergence of the Integral Type Lupas-Bezier Operators[J].Far East Journal of Mathematical Sciences,2008,(1):189-196.
[6]王平华.有界变差函数的Durrmeyer-Bézier算子收敛阶的估计[J].大学数学,2007,(1):75-78.
[7]王平华.对积分型Lupas-Bézier算子收敛阶的估计[J].数学的实践与认识,2009,(18):139-143.
[8]林正炎,白志东.概率不等式[M].北京:科学出版社,2006:9-33.
ESTIMATION ON THE CONVERGENCE RATE OF THE INTEGRAL-TYPE LUPAS-BéZIER OPERATOR
HUANG Kun-yang
(School of Mathematics&Computer Science,Quanzhou Normal University,Quanzhou Fujian 362000)
In this paper,using the probabilistic property of the probabilistic operator,this paper studies the accurate estimation of the convergence rate of the Integral-type Lupas-Bézier operator for the locally bounded variation function.This study is important for the research of the Bézier operator approximation and improving the accurate estimation of CAD geometric model through using the Bézier way.
Integral-type Lupas-Bézier Operator;convergence rate;estimation
O174.41
A
1672-2868(2015)03-0012-04
责任编辑:陈侃
2015-02-11
黄坤阳(1974-),男,福建泉州人。泉州师范学院,讲师,硕士。研究方向:应用数学。
——泉州宋船

