基于FLUENT的TIG焊接电弧数值模拟＊

杨晓锋，周灿丰

（1.北京化工大学 机电工程学院，北京100029；2.北京石油化工学院 机械工程学院，北京102617）

惰性气体保护焊（tungsten inert gas，简称TIG）因其较高的焊接质量和稳定的电弧长度被广泛应用于焊接行业。焊接电弧物理特性可直接影响熔池表面的热流分布，进而影响到电弧与熔池之间的热传递，对焊缝的成形和质量具有决定性的作用。在实际焊接过程中，电弧具有很高的温度以及强烈的弧光，电弧物理特性很难通过试验方法一一确定。采用模拟软件进行数值模拟对于焊接现象进行研究是一种行之有效的方法，同时可以大幅度节约人力、物力和时间，降低工业成本。本文选用FLUENT软件，采用数值模拟的方法为TIG焊接电弧特性进行研究，为焊接过程控制和改进提供了理论依据［1－2］。

1 数学模型

焊接过程中产生的等离子体属于低温等离子体，其温度在2 000～25 000K，在研究TIG焊接等离子体的过程中，一般不考虑等离子体的波动现象［3］。通常把其看成是由导电粒子所组成的流体，在仿真研究的过程中，作为磁流体来处理。数学模型如图1所示，其中，HI为钨极尖端，AB为钨极半径，DG为阳极。

图1 电弧数学模型

1.1 基本假设

在TIG焊接电弧的模拟过程中，对其做如下假设：焊接电弧为光学薄；电弧处于局部热平衡（LTE）状态；忽略电弧等离子体的重力；等离子体流不可压缩；流动状态为层流［4－5］。

1.2 控制方程组

1）磁流体方程组。电弧仿真过程中涉及到电磁学与流体动力学2种理论［6］。

质量连续方程为：

动量方程的径向表达式为：

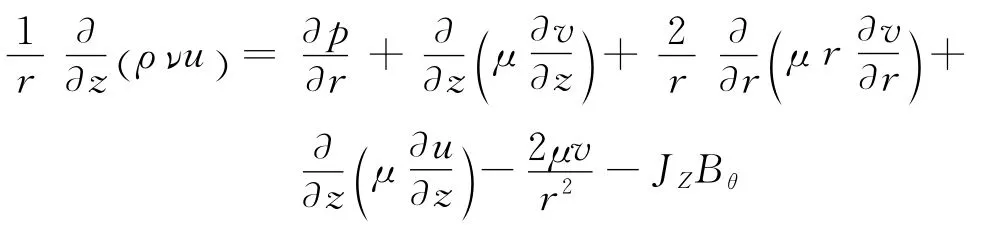
动量方程的轴向表达式为：

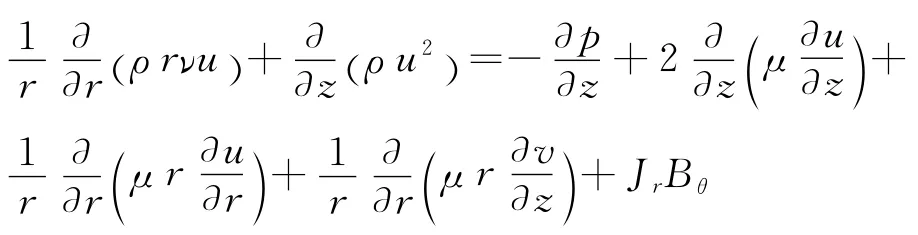
能量守恒方程为：

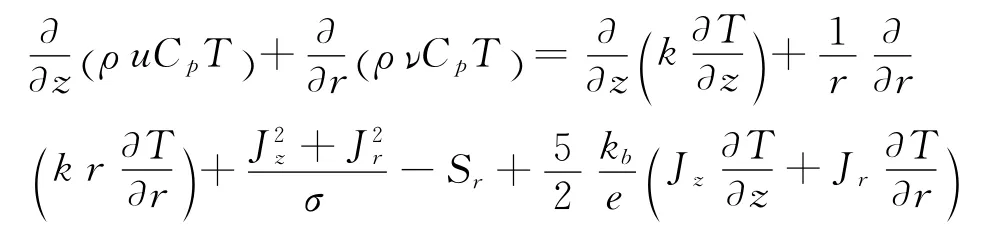
式中，ρ是密度；μ是黏度；Cp是比热容；k是导热系数；P是压力；T是温度；v是速度。

2）麦克斯韦方程组。

电流连续方程：

欧姆定律：

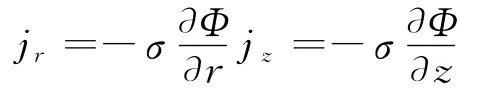
安培环流定律：

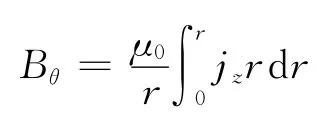
式中，Φ是电势；σ是电导率；μ0＝4π×10－7，表示真空磁导率。

1.3 边界条件

焊接电弧数学模型边界条件见表1。

表1 边界条件

氩元素在高温状态下才具有导电性，设置弧柱区的温度赋值为10 000K。

1.4 Gambit前处理

使用前处理软件Gambit对电弧建模并划分网格，保护气流量为20L／min，保护气体为氩气，钨极半径为2.4mm，尖端直径为0.8mm，弧长为10 mm。网格划分如图2所示。

图2 网格划分

2 FLUENT计算结果与分析

2.1 电弧温度场分布

焊接电流恒定为200A，使用FLUENT软件数值计算得到TIG焊接电弧温度场分布如图3所示。模拟结果表明，在靠近阴极区域，温度达到最高值（22 000K左右），这与实际测量所得的温度值基本相符，电弧温度由钨极向阳极及径向方向逐渐发散，温度下降的速度呈梯度逐渐减小。温度场中，高温区域所显示的形状基本呈扇形，这与焊接时的电弧形状基本相符。

图3 TIG焊接电弧温度场分布

2.2 电弧电势场分布

TIG焊接过程中形成电弧的主要原因是存在着电势差，在电势差的驱动下，阴极和阳极之间形成了电流，同时形成了电磁场。电势场的分布如图4所示，在阴极附近，电势线密集，电势差较大，电势随着离开阴极距离的增大而逐渐发散，这样的电势差分布导致阴极区域电流强度和电流密度较大。

图4 电势场分布

2.3 电弧等离子体速度场分布

在电磁场的作用下，电弧中的等离子体受到洛伦兹力的作用从阴极向阳极高速运动，如图5所示。电弧阴极附近具有较大的电势差，阴极区域的等离子体流动速度迅速增大，并在阴极附近达到最高速度，可达322m／s。当电弧等离子体运动到阳极时，对阳极造成冲击，形成电弧压力，与此同时，由于阳极阻力，电弧等离子体的速度迅速下降。在轴向方向上，偏离中心轴线越远，电磁力越弱，电弧等离子体的运动速度越小。

图5 速度场分布

3 结语

本文以TIG焊接电弧为研究对象，建立了二维TIG焊电弧数学模型，并合理假设了钨极形状。采用有限元数值模拟的方法，利用FLUENT仿真软件，得到了焊接电流为200A条件下TIG焊接电弧的温度分布、电势分布和等离子体速度场分布。从模拟结果可知，TIG焊接过程中阴极附近电弧温度较高，电势差较大，电弧等离子体在这个区域达到最高的运动速度，并逐渐向阳极发散。

［1］贾海棠.K－TIG焊接电弧特性的数值分析［D］.兰州：兰州理工大学，2011.

［2］Hsu K C，Etemadi K，Pfender E.Study of the freeburning high－intensity argon arc［J］.Journal of Applied Physics，1983，54（3）：1293－1301.

［3］乔慧娟.磁场作用下TIG焊接电弧模拟研究［D］.北京：北京石油大学，2007.

［4］Freton P，Gonzalez J J，Gleizes A.Comparison between a two－and a three－dimensional arc plasma configuration［J］.Journal of Physics D：Applied Physics，2000，33（19）：2442.

［5］范红刚，陆家榆，史耀武.直流TIG焊接电弧的数值分析［J］.海军工程学院学报，1996（3）：32.

［6］Schmidt H P，Speckhofer G.Experimental and theoretical investigation of high－pressure arcs.I.the cylindrical arc column （two－dimensional modeling）［J］.Plasma Science，IEEE Transactions on，1996，24（4）：1229－1238.