基于低秩分解的信号噪声分离方法

林 劲 张长浩

基于低秩分解的信号噪声分离方法

林 劲 张长浩

在处理随机平稳信号过程中通常要进行噪声分离。基于低秩分解的噪声分离算法，通过将一段目标信号截断构造信号矩阵，并将信号矩阵分解成代表噪声的稀疏矩阵和代表去噪后信号的低秩矩阵，即信号矩阵的低秩逼近，完成信号的噪声分离。该方法需要经过几何校正和低秩分解两个步骤，在几何校正的过程中同时完成低秩分解。实验表明该算法收敛性好，耗时少，有较高的精确度和效率。

应用背景

在图像信号处理中，常见的处理手段是将二维的图像信号直接转换为图像矩阵，进行各种代数变换或矩阵分解提取图像特征。经典的基于低秩分解的图像信号噪声分离方法采用的就是奇异值分解的方法，利用奇异值这一代数特征作为图像的唯一特征。该方法只进行奇异值分解，省略了特征提取和匹配的步骤，而是利用数学的降维思想，直接实现特征提取，同时分离噪声。实践证明该算法耗时少，收敛性快，对于大块的稀疏噪声有较强的检测和校准能力，目前在图像处理领域已得到广泛应用。受此启发可将该算法从传统的图像信号处理延伸到一般的平稳信号处理中，验证其适用性。

对于一段随机平稳信号，算法的研究对象是该信号截断之后的一系列子信号。不同于基于信号的内容或者信息的某些局部表征，算法试图从信号的全局出发，以数学的角度看待信号矩阵，从高维数据降维这一基本数学思想出发，研究信号的代数特征。具体实现上，它用一个低秩的模型去逼近信号矩阵所代表的高秩模型。通过低秩分解实现信号的噪声剔除，最后用低秩模型恢复原始信号。

低秩分解模型

模型建立

将原始信号均匀截断成由若干子信号组成的集合，并表示成一个矩阵，矩阵的每一列代表每一子信号。在极端理想的情况下，子信号集合中每一子信号都是一样的，那么得到的矩阵的秩应该为1。换而言之为了使得信号矩阵的秩尽可能逼近为1，需要对信号矩阵作几何校正以排除各种畸变影响。同时对信号矩阵进行奇异值分解，并进行奇异值压缩降维，用被保留的奇异值重新生成一个新的秩比较低的矩阵来代替原始矩阵，用新的低秩矩阵重新构造原始信号以达到噪声分离的目的。由于不同信号之间差异总是存在的，理想条件总是不能达到，但是这不妨碍选择矩阵的秩作为衡量子信号相似性的原则。即使达不到理想条件，仍然可以用一个低秩矩阵去表示一个经过良好噪声分离的信号。因此各子信号之间差异性越小则原始信号矩阵D的秩越低，而这一点也即判断信号是否完成噪声分离的标准。

要用一个低秩模型去逼近一个高维的数据模型，也即矩阵D的降维：

算法所讨论的低秩分解模型，是基于几何校正的低秩分解。因此在降维之前，有必要对子信号进行校正。我们先定义算子“˚”表示矩阵的几何校正运算，并假设A表示经过校正之后的信号矩阵，那么问题（1）可以转化为如下形式：

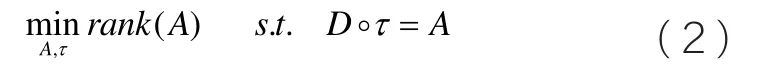
对于式（2），矩阵A代表的经过几何校正的信号矩阵，而不是最终完成噪声分离的低秩矩阵。在低秩分解实现噪声分离过程中，假设ej代表任意一个子信号Ij的噪声，即可代表经过噪声分离之后的n个子信号，把这样的噪声ej统一到一个矩阵E中，将式（2）改写成如下形式：

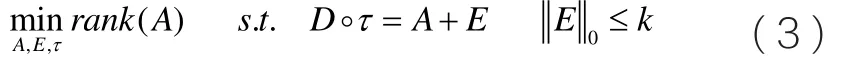
引入参数γ的目的是为了平衡该目标函数。为了避免该问题最终转化为半定矩阵的求解，引入奇异值分解理论，用奇异值分解替代广义拉格朗日乘子法中的迭代计算，最终实现拉格朗日函数局部极小点的求解，进而求解该凸优化问题，实现低秩分解，达到信号噪声分离。

模型求解

几何校正的实质是信号变换，目的是去除信号畸变影响和其他干扰混叠。假设

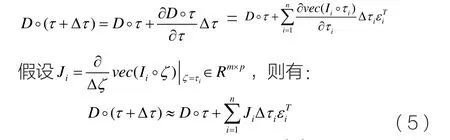
Ji是第i个子信号的雅克比式子。｛εi｝是一个列向量，它是n维空间的一个基向量。

于是问题（4）可以表示成为：

至此，我们就将该优化问题的约束条件通过高斯线性迭代，实现了线性逼近。

对（6）的目标函数进行凸性松弛，简化成易于优化的凸性问题：

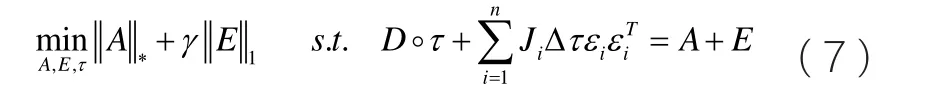
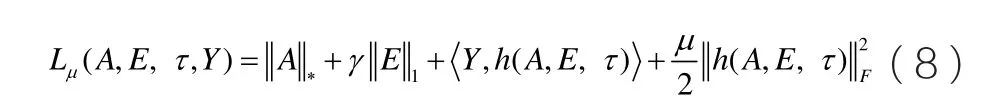
这样，我们就将问题（8）转化为如下的：

问题9）变成一个含三个变量的无约束最优化问题。可分解为如下问题：

可以将问题（10）就从一次迭代计算三变量的问题分解为三次迭代计算单变量的问题，最后采用奇异值分解将问题简化。此处给出完整算法的流程。

Step1 有n个子信号I1,...,In，各子信号所对应的初始化几何变换τ1,...,τn，比例系数λ〉0；

Step2 首先进入外部主循环，判断收敛条件是否达到，如果不收敛，转Step3；否则结束循环，输出式（4）的解A∗, E∗,τ∗。

Step3 计算各子信号进行几何校正的雅克比式：

Step5 进入内部循环，判断内部循环是否收敛达到，如果不收敛，转Step6；否则结束内部循环，输出（4）式的解A∗, E∗,τ∗，转到Step8。

Step6 令k等于0，进行第一次迭代运算。给出Ak, Ek,Δτk的初值。对当前迭代中A的估计进行奇异值分解：

从分解得到的奇异值中选择符合要求的若干奇异值，重构低秩矩阵形成Ak+1；并得到：

Step7 更新拉格朗日算子，Yk+1=Yk+ukh( Ak+1,Ek+1,Δτk+1)，转到Step5；

Step8 更新几何变换算子τ∗，转到Step2。

算法试验验证

验证1

为了对算法的效果有直观认识，首先将该算法应用在经典的图像处理上。

图1是输入图像集，该图像集是同一个人在不同光照背景、角度下拍摄所得，并将每幅人物头像作不同角度轻微旋转。图1中第1行第1列头像右眼被噪声覆盖，第4行第9列面部被噪声覆盖，第7行第1列头像被上下颠倒等等。图2是经过算法噪声分离之后的图像。图3是所分离的噪声。在图3中可以清晰地看到被噪声所覆盖的眼睛、嘴巴等，均可在图1中找到清晰的对应关系。由此可见该算法具有很强的噪声分离能力。

图1　

图2　

图3　

图4　

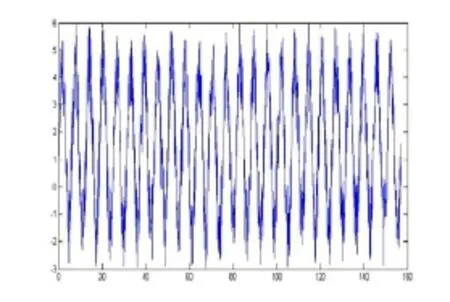
图5　

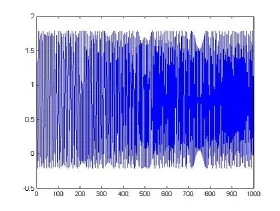
图6　

图7　

验证2

在验证1的基础上考虑对一般信号进行算法验证。

（1） 图4为含高斯白噪声的单频正弦信号，长度160000点，将其截断成4000*40的矩阵，利用以上公式中的求解算法进行噪声分离，将算法输出的低秩矩阵拼接重新生成信号，如图5所示。

（2） 构造线性调频信号，起始频率100Hz，带宽200Hz，添加高斯白噪声，其时域信号和频谱分别如图6和图7所示。

经过算法处理之后的时域信号和频谱如图8和9所示。

对比图6和图8，信号经过算法处理后，噪声分离效果良好，在100Hz到300Hz范围频谱明显得到增强，可见该算法具有较好的噪声分离能力。

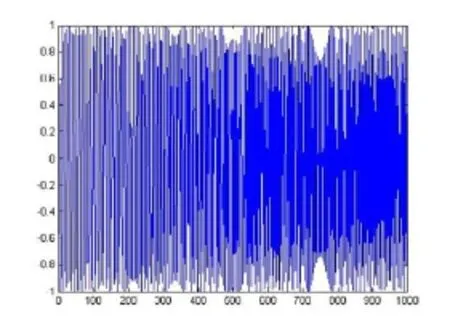
图8　

图9　

结语

从图像处理领域延伸而来的基于低秩分解信号噪声分离算法，拓展到一般的信号处理上，仍然具有一定的适用性。使用经典的图像信号进行算法验证时，其效果一目了然。使用正弦信号验证时，经过算法过滤后的信号波形清晰，使用线性调频信号验证时，对比算法处理前后，其频谱具有明显改观，可见算法效益明显。当然对于更一般的随机平稳是否扔具有如此强的效果值得进一步探讨，乃至对于非平稳的信号算法是否依然可用都值得作进一步探讨。

10.3969/j.issn.1001-8972.2015.21.004