基于先验信息的脑图像数据信息提取算法

冯 宝，刘晓刚

（桂林航天工业学院自动化系，广西桂林541004）

基于先验信息的脑图像数据信息提取算法

冯 宝，刘晓刚

（桂林航天工业学院自动化系，广西桂林541004）

传统稀疏表示方法选择出的脑激活体素空间分布过于稀疏，不具有空间团块特性，在分析真实数据时的性能较低。针对该问题，提出一种基于先验信息的脑激活体素选择算法。该算法结合脑图像数据的高维性特点，以张量分析为基础，建立脑图像数据与任务函数之间的回归模型。用凸优化技术将脑激活体素的空间团块特性以凸约束的形式整合到体素选择过程中，使得该算法更加适合脑图像数据的信息提取，并采用脑激活区定位和解码实验对算法进行验证。实验结果表明，与传统稀疏表示算法相比，该算法选择出的脑激活体素空间分布更集中，在解码分析中能获得较高的解码准确率，在脑图像数据分析时表现出较高的求解质量和求解效率，能有效分析脑图像数据。

体素选择；稀疏表示；功能核磁共振成像；张量表示；脑激活区定位

1 概述

众所周知，人脑是迄今为止人类所知道的最复杂、最精密的系统。大脑对信息的快速处理依赖于大脑系统中高效的信息处理机制。对脑信息处理机制的研究不仅有助于深入了解人脑的信息加工和处理过程，而且有助于提升现有的信息科学理论与技术水平，为当前信息科学相关领域（如航天电子信息等）的关键问题提供技术借鉴。

功能核磁共振成像（functional Magnetic Resonance Imaging，fMRI）技术对于探索人脑功能以及人脑信息处理机制至关重要［1-2］。目前，体素选择（也可称为脑激活区定位）是fMRI数据分析的一种主要方式［3］。如何准确地找到与实验任务相关的激活体素对于脑科学研究至关重要，这也是fMRI体素选择分析的主要目的。

为了准确地从大脑中选择出与实验任务相关的激活体素，需要根据人脑激活过程确定合理的先验信息，并以此来设计合适的体素选择算法。目前稀疏表示算法，在fMRI数据分析领域受到了广泛关注。传统的稀疏表示算法即最小收缩选择算子（Least Absolute Shrinkage and Selection Operator，LASSO）算法［4］，主要利用激活体素的空间稀疏特性来对fMRI数据进行分析。近期的研究发现，单个激活体素无法完成某一特定生理任务，不具有生理意义和研究价值，而有研究价值的激活体素往往是以团块（Cluster）的形式出现［5-6］。然而，传统的稀疏表示算法在进行激活体素选择时，仅考虑激活体素的空间稀疏性而忽略了其空间团块特性，导致算法在分析真实数据时性能下降［7］。

研究表明，当激活体素在空间分布上形成一个团块时，处于同一团块中的激活体素激活程度相近，因而其所对应的回归系数值大小也相近，表现出空间平滑的特点。在数学上，这种平滑特点可以用多维空间导数来进行描述。因此，通过在原有稀疏表示优化模型中增加平滑性约束条件，可以使得新算法选择出的激活体素不但保持空间稀疏特性，还具有空间团块特点。

为了解决传统稀疏表示算法在fMRI数据分析中存在的问题，本文提出一种基于多维导数约束的鲁棒稀疏体素选择（Robust Voxel Selection Method with Multi-dimensional Derivative Constraints，RVSMDC）算法。与传统fMRI数据分析算法不同的是，新算法的设计采用张量表达的方式。由于fMRI数据是一个天然的四阶张量，采用张量技术对其分析，因此能够很好地保持fMRI数据空间结构信息不被破坏，此外，用张量技术分析高维数据，有利于引入激活体素空间团块特性这一先验信息。

2 脑激活体素选择算法

2.1 fM RI信号模型

基于稀疏表示算法的fMRI数据信号模型是一个fMRI数据与任务函数之间的回归模型，可以表示为：

体素选择分析的主要目的是从大脑中寻找出M（M≤I1×I2×I3）个被实验任务所激活的体素。由于张量矩阵ω的每个元素反映了体素对于实验任务的重要程度，因此可以将ω中较大的值所对应的体素选为激活体素（权重系数越大，表明该体素对实验任务越重要）。此外，由于大脑中包括了上千万个体素，而激活体素只是占了所有体素中的少数（表现出稀疏特性）。因此，权重系数ω中的大部分值是为零的，只有一部分值非零。所以，基于稀疏表示算法的fMRI体素选择分析可以用如下的数学优化表达式来表示：

2.2 基于多维导数约束的稀疏体素选择算法

研究发现，传统的稀疏表示算法存在一些可以改进的地方：首先，传统的稀疏表示算法在进行fMRI模型构建的过程中并没有加入对模型误差的考虑，在一定程度上降低算法的性能。为了进一步改善这一缺点，在RVSMDC算法中引入了误差容忍机制：

其中，εt为一向量，其标准差为σ。

为了使RVSMDC算法对于不同类型的误差都具有鲁棒容忍能力，将fMRI信号模型式（1）改为：

在增加了误差容忍机制之后，稀疏表示算法的优化表达式（2）可以进一步表示为：

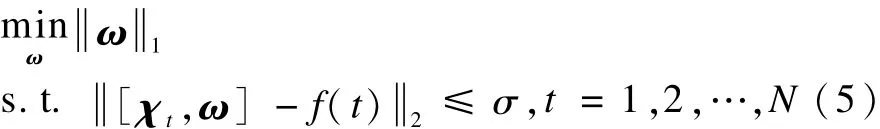
研究表明单个激活体素不能够完成一项有意义的任务，因此，有研究价值的激活体素都是以团块的形式分布在脑区中的［9-11］。为了使RVSMDC算法同时获得空间稀疏特性和空间团块特性。对处于同一团块中的激活体素进行了研究，并发现当激活体素处于同一团块中时，它们所对应的回归系数ω具有平滑特性。在数学上，ω的平滑特性可以表示为函数Sm（ω）：

其中，U1∈R（I1-P）×I1，U2∈R（I2-P）×I2，U3∈R（I3-P）×I3表示大脑所处三围空间中轴向、冠状、矢状3个维度方向上体素空间导数矩阵；P是空间导数的阶数。在实际应用中，矩阵Ui，i=1，2，3可以是一阶或者二阶导数矩阵。本文采用了一阶导数矩阵，该导数矩阵是通过激活体素的空间分布来求得的。

综上所述，适合fMRI体素选择分析的算法应该同时考虑到激活体素空间稀疏特性和空间团块特性。因此，在RVSMDC算法的优化表达式中，同时最小化ω的L1范数和Sm（ω）：

其中，α1是关于激活体素的空间稀疏特性和空间团块特性的一个正则化参数。

3 实验结果与分析

为了验证算法的可行性和有效性，将本文算法与传统稀疏表示算法［12］同时应用在真实fMRI数据集上。

3.1 数据描述

在数据选择方面，采用了匹兹堡大学于2007年举办的一次fMRI数据分析竞赛（Pittsburgh Brain Activity Interpretation Competition 2007，PBAIC2007）。PBAIC2007实验数据是在西门子（Siemens 3（Tesla））磁共振扫描仪中采集的。该数据共包含了3个被试（编号分别为被试13、被试14、被试01）。每一个被试重复进行3次实验，并分别记录了3次实验的完整的fMRI数据。每次实验包含了704个fMRI采样点。在实验过程中，被试者置身于一个虚拟的环境中，并且被要求执行一些不同的任务（如按照提示的命令行走，按照提示的命令捡起虚拟环境中的水果等）。在整个实验过程中，大多数实验任务都是随机给出的［13］，这就为实验数据的分析增加了难度。

3.2 结果分析

实验结果展示方面主要从体素选择和解码分析两方面进行。体素选择分析目的比较明确，即寻找与实验任务最相关的体素作为脑激活体素。而解码分析可以看作是体素选择分析的深入。解码分析主要是通过对当前激活体素时间序列的分析来重构任务函数，以此来解码大脑当前的认知状态。在解码分析中，需要建立一个回归模型，模型的输入是激活体素时间序列，模型的输出是解码函数，即对任务函数的预测。解码分析算法的主要目的是获取合理的回归系数来对激活体素的时间序列进行加权组合。因此，解码分析建立了激活体素与任务函数之间的关系。在解码分析中，解码准确率是一个重要的性能评判指标，它主要指解码函数与真实任务函数之间的相关系数。

本文选择被试13的Instruction任务来进行体素选择以及解码分析结果的展示。在体素选择分析方面，传统稀疏表示算法和新算法同时选择了50个激活体素。如图1所示，传统稀疏表示算法选择出的激活体素共分布在15层上，且在16层～26层的分布比较零散。

图1 体素激活的空间分布情况

新算法选择出的激活体素共分布在13层上，显得更加集中，并在一些层（如11层、12层、13层、14层）上形成了团块。尤其从图1中代表第14层（Slice 14）的子图可以看出，新算法选择激活体素形成的团块空间分布更集中，这表明这些团块中的激活体素是有意义的实验任务相关体素（因为单个激活体素无法完成某一特定生理任务，有研究价值的激活体素常以团块形式出现）。因此，新算法选择出的激活体素更加符合脑激活的生理过程，更容易从生理角度对结果进行解释。

在结果分析中还发现，传统稀疏表示算法和本文算法都各自单独找到了一些激活体素。为了验证其有效性，对这些由2种算法单独找到的激活体素做了进一步的解码分析。图2展示了2种算法各自单独找到的激活体素的解码准确率，从图中发现，本文算法单独找到的激活体素，能够以更高的解码准确率来对任务函数进行解码（传统稀疏表示算法对应的解码准确率为r=0.57，本文算法对应的解码准确率为r=0.68）。

图2 体素激活的解码函数对比

此外，由于PBA IC2007数据集中包含了3个被试的多个任务的数据，因此接下来针对不同被试的不同任务分别进行了解码分析。

本文用被试13的Instruction任务和Fruit Anxious任务对应的数据进行了进一步的分析。将所选激活体素的数目设定为一个从1～100递增变化的量，并用选择出的激活体素进行解码分析。图3展示了当激活体素数目从1增加到100情况下的解码准确率，从图中可以发现，与传统稀疏表示算法相比，新算法取得了较高的解码准确率。本文也对被试01的Instruction任务和FruitAnxious任务对应的数据进行了同样的解码分析。从图4可以看出，在大多数情况下，新算法取得的解码准确率要比传统稀疏表示算法高。换言之，新算法选择出来的体素与实验任务更相关。

图3 体素激活的解码准确率（被试13的2种任务）

图4 体素激活的解码准确率（被试01的2种任务）

4 结束语

为了选择出与实验任务相关的激活体素，将合理的先验知识以正则约束的形式引入到了优化过程中，本文提出一种适用于体素选择分析的RVSMDC算法。通过引入误差容忍机制获取对于fMRI数据模型误差的容忍能力，在原有稀疏表示优化表达式中增加对于回归系数的平滑性约束，使得基于RVSMDC算法选择出的体素在空间分布上同时具有空间稀疏特性和空间团块特性。此外，RVSMDC算法是建立在张量分析基础上的，由于fMRI数据具有高维性特点，采用张量技术构建算法可以很好地保护fMRI信号的空间结构不被破坏，有利于发现更好的结果。今后将推进凸优化技术在fMRI数据分析中的运用，继续深入研究fMRI数据的特点，并探索如何将这些特点转换为先验信息，并以凸约束形式进行整合，从而提高算法的分析效果。

［1］ Bandettini P A，Eric W C，Hinks R S，et al.Time Course EPI of Human Brain Function During Task Activation［J］. Magnetic Resonance Medicine，1992，25（2）：390-397.

［2］ 李启虎.人类大脑信号处理机制研究［J］.世界科技研究与发展，1999，21（4）：16-18.

［3］ 袁 宏.fMRI数据分析方法研究［D］.成都：电子科技大学，2005.

［4］ Grosenick L，Greer S，Knutson B.Interpretable Classifiers for fMRI Improve Prediction of Purchases［J］.IEEE Transactions on Neural Systems and Rehabilitation Engineering，2008，16（6）：539-548.

［5］ Forman S D，Cohen J D，Fitzgerald M，et al.Improved Assessment of Significant Activation in Functional Magnetic Resonance Imaging fMRI：Use of a Cluster-size Threshold［J］.Magnetic Resonance Medicine，1995，33（5）：636-647.

［6］ Heller R，Stanley D，Yekutieli D，et al.Cluster-based Analysis of fMRIData［J］.NeuroImage，2006，33（2）：599-608.

［7］ Bunea F，She Yiyuan，Ombao H，et al.Penalized Least Squares Regression Methods and Applications to Neuroimaging［J］.NeuroImage，2011，55（4）：1519-1527.

［8］ 刘亚东，周宗潭，胡德文，等.大脑fMRI数据时/空模式综合分析的一种新方法［J］.中国科学：E辑，2005，34（10）：1139-1147.

［9］ Oikonomou V P，Blekas K，Astrakas L.A Sparse and Spatially Constrained Generative Regression Model for fMRIData Analysis［J］.IEEE Transactions on Bio-medical Engineering，2012，59（1）：58-67.

［10］ Harrison L，Penny W，Daunizeau J，et al.Diffusion-based Spatial Priors for Functional Magnetic Resonance Images［J］.Neuro Image，2008，41（2/3）：408-423.

［11］ 张 波，谢松云，赵海涛.一种改进ICA算法在脑功能区提取中的应用［J］.计算机仿真，2010，27（1）：222-225.

［12］ Li Yuanqing，Nam buri P，Yu Zhuliang，et al.Voxel Selection in fMRI Data Analysis Based on Sparse Representation［J］.IEEE Transactions on Bio-medical Engineering，2009，56（10）：2439-2451.

［13］ Carroll M K，Cecchi G A，Rish I，et al.Prediction and Interpretation of Distributed Neural Activity with Sparse Models［J］.Neuro Im age，2009，44（1）：112-122.

编辑 刘冰

Brain Image Data Information Extraction Algorithm Based on Priori Information

FENG Bao，LIU Xiaogang
（Department of Automation，Guilin University of Aerospace Technology，Guilin 541004，China）

Voxels selected by the traditional sparse representation algorithm s are too sparse in spatial distribution and hard ly show cluster effect，and the analysis performance of the real data is low.To overcome this problem，this paper proposes a prior information based algorithm for useful information extraction from brain image data.Considering the high dimensionality property of brain image data，a regression algorithm between function Magnetic Resonance Imaging（fMRI）data and task function is established by using tenor formulation.By introducing cluster effect of activated voxels in spatial distribution as prior information into voxel selection methods based on convex optimization technique，the proposed algorithms are more suitable for useful information extraction from brain image data.It uses experiments of brain activation localization and neural decoding to evaluate the proposed algorithm.Numerical results show that，compared with traditional sparse representation algorithm，voxels selected by the proposed algorithm are more concentrated in spatial distribution.It achieves higher decoding accuracy for decoding analysis.The proposed algorithm has high quality solution and can reliably process the brain image data.

voxel selection；sparse representation；function Magnetic Resonance Imaging（fMRI）；tensor representation；brain activation area location

冯 宝，刘晓刚.基于先验信息的脑图像数据信息提取算法［J］.计算机工程，2015，41（9）：194-198.

英文引用格式：Feng Bao，Liu Xiaogang.Brain Image Data Information Extraction Algorithm Based on Priori Information［J］.Computer Engineering，2015，41（9）：194-198.

1000-3428（2015）09-0194-05

A

TP393.41

10.3969/j.issn.1000-3428.2015.09.036

广西高校科学技术研究基金资助重点项目（KY2015ZD143）；广西高校机器人与焊接技术重点实验室培育基地基金资助项目；桂林航天工业学院博士启动基金资助项目。

冯 宝（1986-），男，讲师、博士，主研方向：模式识别，脑信号分析，凸分析与优化；刘晓刚，教授、博士。

2014-10-19

2014-11-10 E-m ail：fengbao1986.love@163.com