预警机群信息化装备能执行任务率的系统设计
丁定浩
预警机群信息化装备能执行任务率的系统设计
丁定浩
美国空军的预警机联队通常由4架机组成,对规定的海空领域的目标进行探测与定位,引导与指挥战机进行拦击或攻击。国外在效仿美国组建预警机群时,通常预警机联队也以4架机组成。实际上,预警机联队的数量,必须由适应任务环境的各种需求、预警机及其信息化装备的使用有效性等条件来确定。配置不当,出现预警黑洞,可能发生严重的后果;反之,闲置不用,积压可观的资源又会造成浪费。当前,美国预警机群以能执行任务率为目标,使用仿真试验来确定预警机的数量。正确性如何,无法考证。研究开发计算机辅助专用设计分析软件,直接从计算任务期内平均工作时间入手,实现预警机的信息化装备的系统设计。
预警机群;能执行任务率;任务时间的平均工作时间;预警黑洞
0 引言
能执行任务率参数,最早被美国空军作为可靠性、维修性、保障性顶层参数之一,并列入空军军机系列指标之中;它的定义是在整个寿命周期内任务持续时间中实际能执行任务的平均时间与要求任务持续工作时间之比。但美国空军对此只给出定义,没有提供解析模型。
因此,在预警机群的系统设计中,美军只能采用计算机辅助作数字仿真。计算机数字仿真的正确性,完全取决于仿真模型能否正确地反映客观的实际过程,而仿真模型一般又不进行公开评审,任何局部不符合客观过程的仿真模型,其可能带来与实际大相径庭的结果,从而产生严重的后果。。
另一方面,就是如何论证能执行任务率的定量指标的确定。实际上,这应该从论证任务时间中能容忍出现预警黑洞时间为依据。预警黑洞时间就是相关区域丧失预警功能的时间。因此,论证能执行任务率指标,应该由任务持续工作时间ts中容忍出现的黑洞时间的数值来确定。
不难理解,预警黑洞时间th等于:
th=ts-t(1)式 (1)中:ts——要求承担区域预警任务的持续工作时间;
t——在任务持续工作时间内能够实际执行任务的时间,这一时间与承担预警任务的信息化装备的任务可靠度有关。
能执行任务率与任务成功率是有区别的。任务成功率在任务持续时间内一旦发生丧失规定的功能就视为一次任务完全失效,而能执行任务率在任务持续时间内发生失效,它在发生失效时刻以前的工作时间是有效的。失效持续时间的长短,即预警黑洞时间才是关注的焦点。不难明白,预警机信息化装备在任务时间内发生失效,对前面执行的任务没有影响,当其他预警机信息化装备接续工作,对整体任务是没有影响的。
1 能执行任务率的参数模型
复杂系统的能执行任务率MCR的解析模型,笔者已经导出[1]:
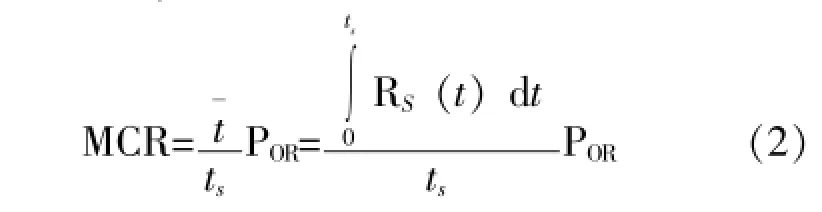
式 (2)中:Rs(t)——复杂系统的任务可靠度;
POR——复杂系统的战备完好率。
式 (2)中的复杂系统的任务可靠度的通用模型为:

式 (3)中的第1个连乘符号表示有ns1个串联结构,第2个连乘符号表示有ns2个并联结构,第3个连乘符号表示有ns3个表决结构;R1R2…Rm表示有m个其他结构的可靠度结构模型。
式中战备完好率模型更加复杂,对备件的不同性质 (消耗、可修)、备件供应的不同体制 (现场、供应站两站制,近距离库房、供应站两站制,现场、库房、供应站三站制,现场、中继站、供应站三站制),以及备件补充的不同方式 (定期补充,实时补充和定数补充)有不同的解析表达式,见文献[2]。
能执行任务率模型中的战备完好率参数,是保障系统在整个寿命周期中各个任务持续时间中能执行任务率保持不变的前提[3]。
2 预警机群信息化装备的系统设计
预警机群信息化装备的系统设计,就是在已知单套预警机信息化装备的可靠性、维修性、保障性的条件下,根据任务需求,在满足能执行任务率指标要求的前提下,确定最佳预警机及其信息化装备必要的成套数,并以节约寿命周期费用为目的,进行备件优化配置设计[4]。
首先要论证能执行任务率指标的定量要求。前面已经说过,要从任务持续时间内能容忍的预警黑洞时间出发。
对上述能执行任务率模型改写为下列形式:
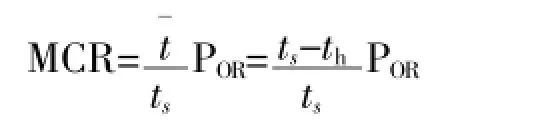
并设定预警机群的战备完好率,即可确定能执行任务率指标要求。设任务持续时间ts为24 h,容忍预警黑洞时间th为20 min,要求战备完好率POR为0.995,则能执行任务率MCR应为0.981 18。
指标确定以后,就要建立预警机群信息化装备的系统设计模型。
当单机可实现能执行任务率指标,则另配一套预警机及其信息化装备,以备替换任务机落地补充能源。系统模型就是单一能执行任务率模型。
当单机无法实现所要求的能执行任务率指标,且飞机从基地飞抵预警区域的时间超过能容忍的黑洞时间,则要求两架机同时在空中执勤。在此条件下的系统模型为:

当任务持续时间较长,两架机也不能实现能执行任务率的指标要求,必须再次增加机群数,在此条件下,不需要也不允许多架机同时执勤,必须在基地待命。
对于3架或更多架次的并联冗余结构中既有热备并联,又有旁并联,没有现成的模型可以套用,当前流行的4套机群就是这一模型,因为其中1套用于替代飞机落地并补充能源之用,实际是3套机群模型,必须另行推导。当单套信息化装备的系统失效率为常数时,可用马氏动态模型建立。以3套装备为例,可得经拉普拉斯变换后的状态转移矩阵如下所示:

由上列状态转移矩阵可以解出:
R3s=4exp(-λsts)-(3+2λsts)exp(-2λts)代入能执行任务率模型得:
MCR=
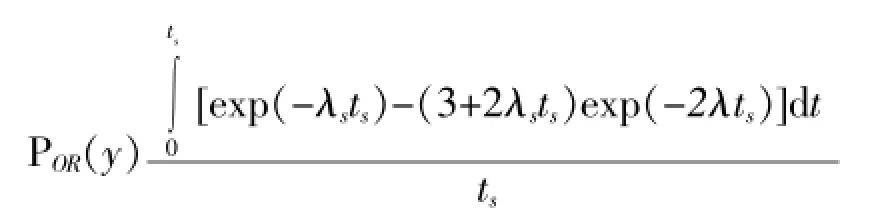
但上式实际上是不适用的。首先,因为复杂的信息化装备的系统失效率不可能是与时间无关的常数,也即包含的现场更换模块全部是串联结构,一旦存在冗余结构,系统失效率为常数的假设就是不成立的;其次,在地面待命的飞机,当值勤机中发生失效需要接替时,需要等待由基地飞抵预警区域的时间因素模型中不能反映,因而上列能执行任务率模型是不适用的。
因此,常规的解析方法无法解出,必须研究编制计算机辅助分析计算软件及数值解法加以解决。
当前,我们已经完成了软件开发,正在解决通用性问题[5]。
4 数字示例
下面用一个虚拟数值示例说明。
我们虚拟预警机信息化装备包含100种类别、239个现场更换模块,其中包括70个单个串联结构,5个多元串联结构,2个并联结构,23个表决结构,各更换模块的失效率、修复率如表1所示[4]。通过复杂系统任务可靠度分析软件,已知在任务持续为6 h条件下,任务可靠度为0.919 7。
为了减轻预警机群的数量,首先要提升战备完好率水平。我们要求这一指标达到0.995。当备件对象为可修部件,备件供应为现场、供应站两站制,备件补充方式为实时时,假设备件的周转时间相同,均为2 190 h;在此条件下,战备完好率设计软件的输出结果因现场更换模块的修复率限制,战备完好率最高为0.982,备件总数为616件。为此,我们运用战备完好率全面设计软件,即对备件和维修保障同时进行设计。软件输出对各更换模块的修复率和备件分别要求如下。
a)各现场更换模块的每小时的修复率提升到下列数值:
.38.33.38 1.11 1.12.83 2.4 1.32.55.62 .31.121.51.011.191.191.19.9.55.83 1.01.83.83.69.54.62.44.44.62.9.9.9. 59.791.452.121.43.4.591.461.461.42 1.05.9.9.9.9.9 1.13 1.46 1.05 1.25 1.25. 621.251.05.621.13.31.83.691.181.58 1.32.77 1.37.99.3 1.26.3.96.74.79 2.28 1.71.7.9.91.41.761.511.121.561.33 1.33.25 1.75.71.95 1.39 1.02.25.86.33. 33 1.04 1.37.9.9.97
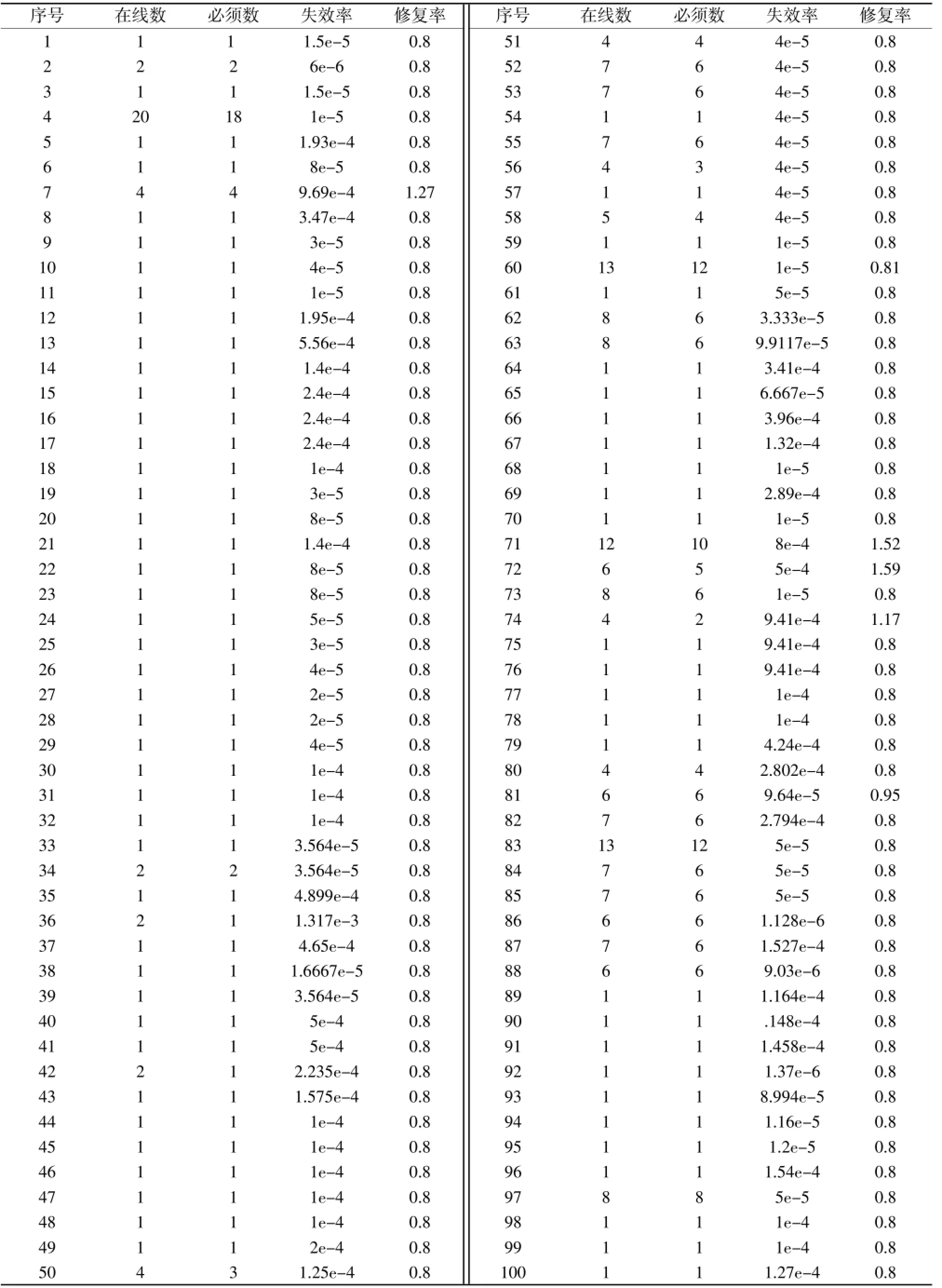
表1 100种现场更换模块的各种数据
b)现场备件的最佳配置为:
3 3 3 7 7 5 42 10 3 4 2 7 12 6 8 8 8 6 3 5 6 5 5 4 3 4 3 3 4 6 6 6 4 5 11 28 11 3 4 11 11 11 7 6 6 6 6 6 7 11 7 9 9 4 9 7 4 7 2 19 4 8 13 9 5 10 6 2 9 2 6 5 5 36 16 16 6 6 10 17 12 7 13 10 10 2 17 4 6 10 6 1 5 2 2 7 10 6 6 6
备件总计为771件。
备件采用实时补充方式,就是当现场任一备件减少时,要保障在2 190 h后得到补充。
下面分析由上述信息化装备组成的预警机群。
a)假设基地飞机飞达规定区域的时间为1.5 h,任务之间容许的停机时间td=2 h。
b)预警机群为2(不计接替能源补充的飞机在内,以下同)的条件下,任务持续时间ts分别为12、24、36 h,能执行任务率MCR和黑洞时间th分别为:
1)ts=12 h,能执行任务率MCR=0.987 03,黑洞时间th=5.766 8min;
2)ts=24 h,能执行任务率MCR=0.964 29,黑洞时间th=23.26 min;
3)ts=36 h,能执行任务率MCR=0.933 05,黑洞时间th=134.47min。
c)预警机群为3的条件下,任务持续时间ts分别为12、24、36 h,能执行任务率MCR和黑洞时间th分别为:
1)ts=12 h,能执行任务率MCR=0.994 19,黑洞时间th=0.58min;
2)ts=24 h,能执行任务率MCR=0.990 99,黑洞时间th=5.79min;
3)ts=36 h,能执行任务率MCR=0.981 89,黑洞时间th=22 min。
d)预警机群为4的条件下,任务持续时间ts分别为12、24、36 h,能执行任务率MCR和黑洞时间th分别为:
1)ts=12 h,能执行任务率MCR=0.999 97,黑洞时间th=0.02min;
2)ts=24 h,能执行任务率MCR=0.994 67,黑洞时间th=0.478 min;
3)ts=36 h,能执行任务率MCR=0.993 67,黑洞时间th=2.87min。
由此可见,预警机及其信息化装备配置,不存在固定模式,完全由任务剖面、任务要求的持续时间、基地离规定区域的飞行时间,预警机及其信息化装备的可靠性、维修性和备件保障性水平决定。
5 结束语
对预警机群的系统设计,涉及复杂冗余系统的动态检修过程,这一计算机辅助设计软件的研究编制完成,使这一复杂系统的可靠性、维修性、保障性的全面设计得到快速的实现,保障在最经济条件下实现预警机群信息化装备的配置设计。
[1]丁定浩.能执行任务率模型 [J].电子产品可靠性与环境试验,2011,29(6):1-5.
[2]丁定浩,陆军.装备寿命周期使用保障的理论模型和设计技术 [M].北京:电子工业出版社,2011.
[3]丁定浩.RMS一体化设计及其验证方法 [J].电子产品可靠性与环境试验,2014,32(1):1-5.
[4]丁定浩.备件配置的优化设计探讨 [J].电子产品可靠性与环境试验,2015,33(1):1-6.
[5]丁定浩.预警机群能执行任务率系统设计软件 [Z].
The System Design of Mission Capable Rate of AWACS Fleet's Inform ation Equipment
DING Ding-hao
A USAF AWACS fleet usually consists of four aircrafts,which can be used to detect and orientate the targets in the specified naval and air fields,and guide or direct fighters to intercept and attack.When an AWACS fleet is organized in other countries following the example of the US,usually it also consists of four aircrafts.In fact,the number of the aircraft in an AWACS fleetmustbe determined by the necessary demands,the AWACS itself,the effectiveness of its information equipment,and other conditions.If warning black hole appears because of misconfiguration,it will result in severe consequences.On the contrary,if it sits unused,the considerable resources will be wasted.At present,the number of the aircraft in a USAF AWACS fleet is often determined through simulation experiment on the basis of mission capable rate. However,the correctness of this method can not be verified.Therefore,it is necessary to research and develop the com puter-aided design and analysis software,directly com pute the average operation time in the task period to realize the system design of AWACS' information equipment.
AWACS fleet;mission capable rate;the average operation time in the task period;warning black hole
TB 114.3
A
1672-5468(2015)02-0001-05 doi:10.3969/j.issn.1672-5468.2015.02.001
2014-07-07
丁定浩 (1929-),男,江苏吴江人,中国电子科技集团公司电子科学研究院研究员,上海大学、南京航空航天大学兼职教授,长期从事系统可靠性、维修性、保障性理论和工程设计研究工作。ddh_ddh@126.com

