花岗岩损伤破坏的声发射评价

刘　刚，　张艳军，申志亮，　王一斐，　于　涵，　刘宏伟

（1.黑龙江科技大学 黑龙江省煤矿深部开采地压控制与瓦斯治理重点实验室，哈尔滨150022；2.黑龙江科技大学机械工程学院，哈尔滨150022；3.黑龙江科技大学 矿业工程学院，哈尔滨 150022）

花岗岩损伤破坏的声发射评价

刘刚1，张艳军2，申志亮3，王一斐3，于涵3，刘宏伟3

（1.黑龙江科技大学 黑龙江省煤矿深部开采地压控制与瓦斯治理重点实验室，哈尔滨150022；2.黑龙江科技大学机械工程学院，哈尔滨150022；3.黑龙江科技大学 矿业工程学院，哈尔滨 150022）

为评价花岗岩裂纹扩展对应损伤破坏状况，在单轴压缩方形花岗岩基础上，通过全程应力-应变曲线及声发射信号，利用声发射能量和计数与应力-应变曲线积分得到的能量，基于等时原理进行数据插值，拟合曲线，推导损伤演化方程，以此定量评估不同应力下花岗岩损伤程度。结果表明：花岗岩宏观破坏形态与应力-应变曲线峰值应力瞬时下滑趋势存在一致性。依据能量、声发射计数和声发射能量与损伤程度的数学解析式，与应力-时间曲线结合分析，给出脆性花岗岩损伤三阶段、预警时刻和报警点。根据特征参数优缺点和敏感度，通过损伤时间敏感效应优化处理，划分预警时刻六级区间。分析认为，声发射计数最早报警，声发射能量出现在第二阶段，最终通过能量变化判断花岗岩失稳。

花岗岩；声发射；损伤；能量

0　引言

花岗岩属火成岩，由地下岩浆喷出和侵入冷却结晶形成。由于原生缺陷和原始损伤存在，非均质性及各向异性明显。岩石内部缺陷在载荷作用下张开或闭合、扩展，致使损伤加剧，同时以弹性波形式携带应变能不断向外释放，产生声发射现象。声发射波形蕴含丰富岩石破坏损伤区及内部信息。声发射监测技术对岩石类材料裂纹闭合和扩展十分敏感，被广泛应用于煤矿、天然气和石油存储、辐射废物封存、地热存储、岩石和土体边坡、大坝等损伤渐进破坏监测。故通过声发射技术研究岩石损伤演化规律，能深刻挖掘岩石类材料破坏机制，并为预测预报相关灾害事故打下坚实理论基础。

国内外学者针对岩石类材料声发射损伤破坏规律研究成果非常丰富，但多集中于讨论不同加载应力、控制方式和时间效应下声发射特征参数与损伤规律之间的关系［1-13］。其中，在室内单轴声发射实验方面，徐子杰、李术方和肖福坤等研究了不同应力水平、监测手段、材料、岩石种类、实验路径、分析角度下岩石损伤破坏的声发射规律［1-8］。在三轴声发射实验和现场实验方面，赵洪宝、杨永杰和肖福坤等对型煤和原煤在不同瓦斯压力、围压、开挖尺度下损伤演化声发射规律开展了研究［9-13］。但针对花岗岩损伤演化致破裂过程的定量评估鲜有报道，为此，笔者在单轴压缩方形花岗岩基础上，通过全程应力-应变曲线及声发射信号，利用能量、声发射计数和声发射能量作为损伤参数，从多角度、多层次分析花岗岩损伤演化特征。

1　花岗岩声发射实验

1.1试样选取与制作

实验采用方形花岗岩试件，试件从一块尺寸为50 cm×50 cm×50 cm立方体花岗岩切割制取，选取表面光滑、无明显节理、裂隙试件，从而使实验结果有较高一致性。样品尺寸100 mm×25 mm×100 mm，为避免应力集中并使声发射信号真实准确，利用双端面磨平机对加载端面进行处理，试件两端面平整度小于0.05 mm，轴向偏差小于0.25°，共制取15块标准试件。

1.2加载设备与声发射设备

实验加载装置采用吉林金力技术有限公司生产的TAW-2 000 kN微机控制电液伺服岩石三轴蠕变试验系统，轴向压力达2 000 kN，精度为0.001 kN，位移光码器量程为30 cm，精度达0.001 mm，并能实时采集和绘制全程应力-应变曲线。

实验采用的声发射设备由美国物理声学公司开发的SH-Ⅱ型全天候健康监测系统，该设备可实时采集声发射波形，并对每个波形进行计算，得到计数、能量、幅值、上升时间、定位和峰频等声发射特征参数图，内置波形处理软件。结合实验室环境，声发射门槛值设定为40 dB，前置放大器为40 dB，传感器频率响应范围为125～750 kHz，采样频率为1 MHz，实验采用八个nano30传感器，传感器用皮筋布置在试样某一表面，平面四个，两个侧面各两个，为了增加传感器接收声发射信号的效果，表面涂抹凡士林。为减少压力机端面和试样端面摩擦杂乱信号，试样上下端面均涂抹凡士林。

1.3实验过程

为减小定位结果误差，将试样一面距离端面边缘20 mm处用记号笔定点，两个侧面位置为距离上下端面20 mm且位于布置面中部，用皮筋固定传感器，使其传感器中心与定点位置一致并在接触面涂抹凡士林，利用声发射材料声学矩阵自动测试系统发射标准脉冲检测传感器与试样耦合效果和平均波速，脉冲个数为五个，脉冲宽度为5 μs，脉冲间隔为100 ms。幅值均大于70 dB为耦合良好，记录此时平均波速。在声发射正常采集状态下，采用断铅法验证定位精度。分别对各个面中部位置进行测试，结果偏差小于1 mm为合理。启动压力机，实验采取压力机轴向位置控制方式，加载速率恒定保持在0.002 mm/min，为使接触面密实，预载力设置为0.5 kN。此时，声发射系统和压力机同步开始实验，直至试样完全破坏，同时停止实验。共对15块花岗岩采取单轴压缩声发射实验，文中选取较典型三组实验结果进行具体分析，其他结论类似，不再赘述。典型样品基本物理力学参数如表1所示。

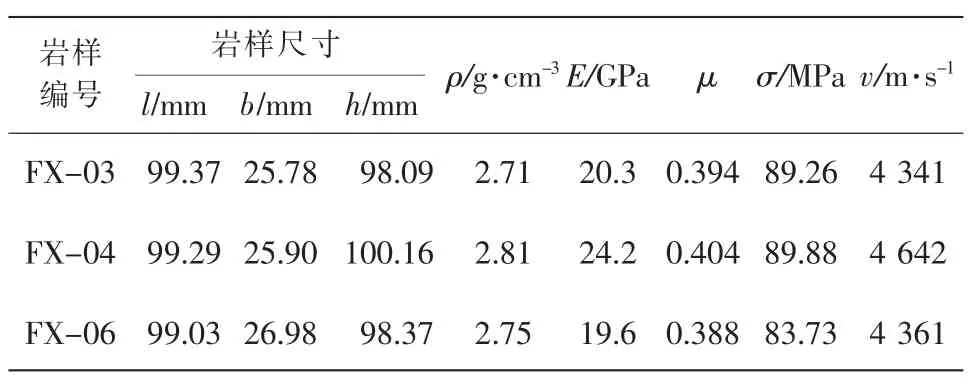
表1　花岗岩基本物理力学参数Table1　Basic physical and mechanical parameters of granite

2　结果与分析

2.1基于能量的损伤评价

图1a为花岗岩破坏全过程应力－应变曲线，图1b为对应的花岗岩破坏形态。由图1可见，峰后曲线出现瞬时局部下滑，实验过程中有清脆断裂声，花岗岩属于脆性破断。将全程应力－应变曲线积聚与释放的能量依据压密阶段Ⅰ、弹性阶段Ⅱ、塑性阶段Ⅲ和峰后阶段Ⅳ划分四个区间。

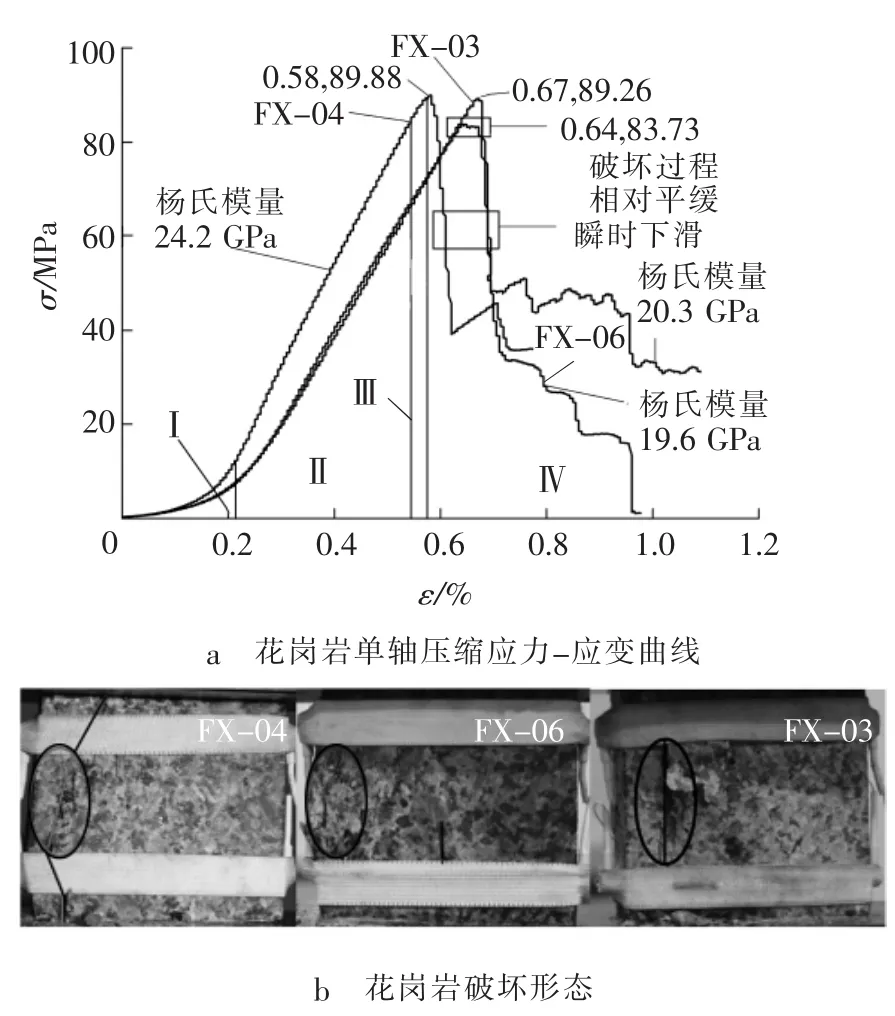
图1　花岗岩单轴压缩应力－应变曲线及破坏形态Fig.1 Granite uniaxial compression stress-strain curves and failure pattern

试件FX－03和FX－04单轴抗压强度分别为89.26和89.88 MPa，结果相近，但弹性阶段斜率相差较大，而FX－06强度低于其他两个试件，杨氏模量与FX－03一致。脆性花岗岩压密阶段明显，弹性阶段较长，塑性阶段极短，峰前积聚大量弹性能，峰后瞬时释放，弹性能部分转化为动能，易造成重大动力灾害，产生严重后果。由于破坏阶段极短且具有超长弹性阶段（积聚弹性能），预判难度极大。通过敏锐性较高的声发射监测手段获取各阶段声发射特征参数变化规律，从而为破坏失稳识别提供指导。从图1b花岗岩破坏形态来看，FX－06左侧集中破碎成小块体，并在中部出现一条未贯通裂纹，曲线峰值阶段出现一段平缓期（图1a），表明微裂纹在此时扩展、贯通，形成局部失稳，峰后仍具有一定承载力。FX－04左侧形成主贯通裂纹，由三段一定角度大裂纹拼接而成，峰值阶段平缓台阶短于FX－06，破碎成三大块体，微裂纹较少。FX－03形成纵向主控裂纹劈裂格局，局部微裂纹较少，从曲线来看，峰值阶段明显出现尖端，破裂也是瞬时失稳。应力－应变曲线和破坏形态有较好的一致性。

能量积聚势必造成压力和变形增大，而应力和变形是致使损伤加剧的主因，用能量表征损伤程度更具有实际意义。图2横坐标加载阶段N为1代表压密完成阶段，2代表弹性完成阶段，3代表塑性完成阶段，4代表峰后整个阶段。花岗岩压密阶段储存的弹性能较少，占峰前积聚能量的4.75%，弹性阶段积聚了大量弹性能，占峰前积聚总能量的86.86%，前两个阶段不计入损伤范畴 （不考虑循环载荷损伤），弹性能卸载后将完全释放，不对花岗岩损伤做功。塑性阶段储蓄能量相对较少，占峰前积聚能量的8.39%，但在极短时间内完成，前期捕捉就尤为重要。峰后阶段较离散，主要是破裂形式和程度不同导致的。花岗岩峰前各阶段能量呈现倒“V”形，压密和弹性区间占据峰前积聚总能量的91.61%，对脆性材料损伤影响极低，可忽略不计，但对基于损伤预判极其重要，据此，从能量损伤比出发，建立损伤判别式，并对图2进行损伤分区，其中一阶段为损伤低影响区，二阶段为损伤影响区，三阶段为损伤加剧区，其中二阶段为警示区，三阶段为报警区。

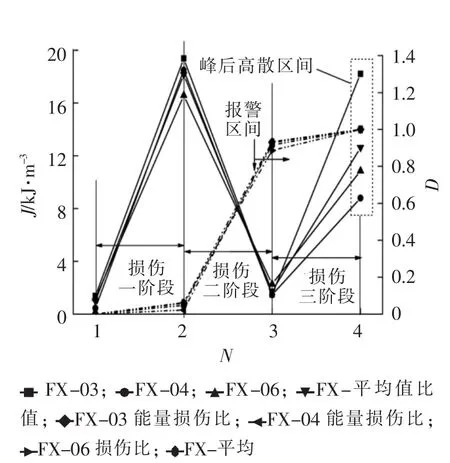
图2　花岗岩各个阶段能量转化规律Fig.2 Granite energy conversion law at various stages

对峰前应力－应变曲线进行积分，获取峰前积聚的总能量，对图1压密阶段、弹性阶段、塑性阶段分别积分，计算峰前积聚总能量与三阶段能量的比，给出能量损伤程度：

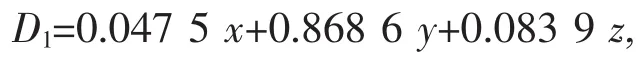
其中，D1为基于能量损伤程度，D1=0表示无损伤，D1=1表示失稳破坏。x、y、z分别为压密、弹性、塑性阶段损伤程度，均属于0到1区间。当为一级损伤时，取值范围0＜x＜1，y=0，z=0。当达到二级损伤时，取值范围x=1，0＜y＜1，z=0。当达到三级损伤，取值范围x=1，y=1，0＜z＜1。预警区间，x=1，0.8＜y＜1，0＜z＜1。

在能量损伤公式的应用过程中，塑性阶段对应时间较短，发生危险可能没有足够长的时间准备，易造成风险，所以笔者建议选取弹性阶段能量80%作为预警点，积聚能量达到该值时，采取减灾、避灾措施。针对脆性花岗岩，能量损伤比处于损伤一阶段波动可以忽视，而达到损伤二阶段引起一定重视，超过74.24%预警值应引起重视，在损伤三阶段波动处于极其危险状态，随时可能发生灾害。通过损伤二阶段塑性转折点划分，结合应力-时间曲线，试样FX－03处于441.57 s为时间预警点，463.17 s为时间报警点，破坏点为471.77 s。通过实验结果和能量损伤比法确定损伤危险分区，可以给出损伤程度值，并提出使用方式和阀值。

2.2基于声发射计数的损伤评价

声发射计数能够体现裂纹扩展释放弹性波波动的强度，也就是说通过声发射计数可以反推裂纹破裂的尺度，声发射计数值越大，内部损伤越剧烈。由于试样呈现相同规律，故选取FX－03进行分析。

依托全程应力－应变曲线，利用origin软件与声发射数据进行插值，得到声发射计数与应力－应变曲线关系，为探索损伤规律的时间效应，将应力－时间曲线与声发射曲线组合分析（图3）。通过声发射计数累计斜率将其分为五个典型阶段，声发射计数稳定增长阶段A、快速增长阶段B、急速增长阶段C、稳定阶段D和峰后线性增长阶段E，峰后线性段公式为

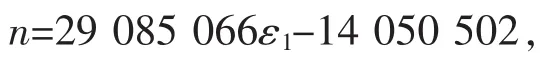
其中，ε1为应变，n为声发射计数。每个对应区间给出变化时间节点。压密阶段和弹性前期阶段共同组成稳定增长期，说明无论载荷大小均造成损伤的加剧。弹性中期为声发射计数的快速增长阶段，此时损伤程度加剧，转折点为峰值强度的74.5%，对应时刻为409.97 s。弹性阶段后期声发射计数急速增长，预示着损伤程度即将达到峰值，失稳前兆信息，分界点为峰值强度的88.4%，对应时刻为441.55 s。当加载时间到471.77 s时，达到峰值89.24 MPa，出现失稳破坏，此时声发射进入约12.48 s稳定期，损伤达到极值时，声发射计数在此阶段基本不再增长，此特性对于鉴别峰后作用明显，也就是说声发射计数快速增大后紧随稳定期，证明此时已经失稳破坏。残余破坏阶段，声发射计数呈现微波动线性增长，裂纹不断扩展贯通形成宏观裂纹。

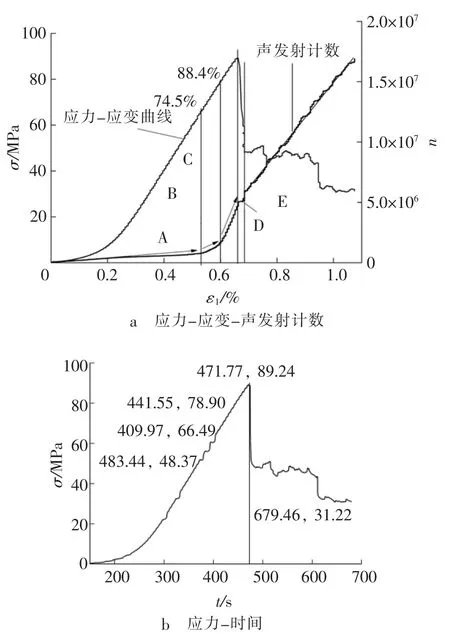
图3　声发射计数-应力-应变-时间关系Fig.3　Acoustic emission counts-stress-strain-time diagram

据此，笔者将峰前划分损伤明显三阶段，逐层递进对损伤程度进行评价，通过声发射计数累计值变化趋势归一化处理与损伤程度进行定量评价，给出三个阶段的分段函数损伤演化规律。损伤一阶段（声发射计数稳定增长期）拟合符合logistic规律（R2=0.991 9），损伤二阶段（声发射计数快速增长期）拟合符合allometric1趋势（R2=0.985 3），损伤三阶段（声发射计数急速增长期）拟合符合allometric1趋势（R2=0.983 3），通过阶段连续化组合得到基于声发射计数全过程损伤演化公式：

其中，a、b、c分别为一、二、三阶段损伤声发射计数累计值，D2为基于声发射计数损伤程度，E为常数10。

2.3基于声发射能量的损伤评价

声发射能量是采集到波形包络线的积分，能体现每个信号源释放的能量，裂纹扩展尺度越剧烈（损伤程度越大），释放弹性波振动幅度越大，所对应能量释放也就越明显，故通过声发射能量表征损伤程度具有合理性。

分析图4可知，曲线变化规律与图3极其相似，按照声发射能量转折点将其划分成五个阶段。声发射能量的稳定期较长，达到峰值载荷的78.6%，时刻为421.66 s，而快速增长期持续时间较声发射计数的短，持续了39.87 s，为预判损伤破坏留出充足时间，在声发射能量表征的急速增长期（峰值载荷96.7%），时刻为461.53 s，持续时间较短，但声发射能量斜率极大，说明声发射能量对损伤破坏前期极其敏感，峰后依然存在稳定期，可以确定其失稳破坏，脆性花岗岩失稳后声发射稳定期与破坏时间基本持平。峰后声发射能量保持线性增长，计算公式为

其中，ε2为应变，j为声发射能量。尽管峰值后总体失稳，但局部依然以裂纹扩展形式释放弹性波，致使局部失稳进一步加剧，最终达到完全破坏。

图4　声发射能量-应力-应变-时间关系Fig.4 Acoustic emission energy-tress-strain-time diagram

依据声发射计数思路，给出损伤演化过程与声发射能量累计值的对应关系：

其中，d、f、g分别为一、二、三阶段损伤声发射能量累计值，D3为基于声发射能量损伤程度，e代表自然对数底数，约等于2.718。

2.4三种评价方法基于时间的优化处理

通过能量、声发射计数和声发射能量分别对损伤破坏程度进行定量评价，损伤程度评价的目的是为预判失稳破坏做准备，预判时间长短能为减灾避灾提供条件，所以基于三种评价方法的优缺点，以时间为节点，综合衡量损伤程度。

以声发射计数最早做出反馈时刻为起点，此时单轴抗压强度为峰值强度的74.5%，对应时间t2为409.97 s。以声发射能量加速增长为第二阶段，此时达到峰值载荷的78.6%，时间t1为421.66 s。以声发射计数急速增长为第三阶段，此时为峰值强度的88.4%，对应时间为441.55 s。以能量为第四阶段，当时间t3达到441.57 s为预警点。以声发射能量急速增长为第五阶段，此时为峰值载荷的96.7%，时间为461.53 s，以能量为第六阶段，当达到463.17 s为时间报警点，最终花岗岩失稳破坏。

通过表2可以直观判断各种评判方法对应的时间，第一次反馈来自声发射计数，第二次反馈来自声发射能量，第三次反馈来自声发射计数，第四次反馈来自能量，第五次反馈来自声发射能量，最终第六次反馈来自能量。综合分析为声发射计数最早报警，声发射能量出现第二阶段，最终通过能量变化判断失稳。

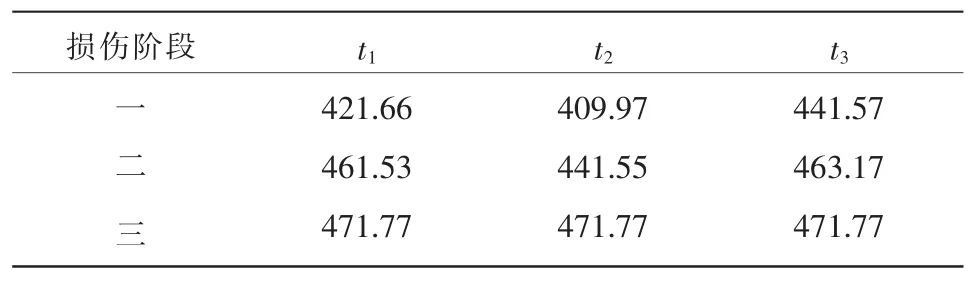
表2　三种评判方法时间关系统计Table 2 Three kinds of evaluation method time statistics s

3　结论

（1）花岗岩宏观破坏形态与应力－应变曲线峰值瞬时下滑速度存在一致性。通过应力－应变曲线积分得到能量变化规律，得到各个阶段能量损伤比与损伤程度对应关系，给出脆性花岗岩损伤三阶段、预警时刻和报警点。

（2）依据声发射计数和声发射能量与应变曲线斜率的变化特征，将曲线分成五个阶段，通过峰前三个阶段得到损伤演化过程中声发射计数、能量分段函数方程。与应力－时间曲线结合分析，给出预判时间点。

（3）通过能量、声发射计数、声发射能量与损伤预警时间点对应关系将其划分预警六级区间。综合分析为声发射计数最早报警，声发射能量出现在第二阶段，最终通过能量变化判断失稳。

致谢：

该研究得到了黑龙江省煤矿深部开采地压控制与瓦斯治理重点实验室开放课题：基于声发射的岩体损伤表征及流固耦合效应研究；国家自然科学基金：冲击地压煤层能量传递与引导规律；国家自然科学基金：煤矿井下应急救援中跨落巷道快速掘进的支持。

［1］徐子杰，齐庆新，李宏艳，等.不同应力水平下大理石蠕变损伤声发射特性［J］.煤炭学报，2014，39（S1）：70-74.

［2］李术方，许新骥，刘征宇，等.单轴压缩条件下砂岩破坏全过程电阻率与声发射响应特征及损伤演化［J］.岩石力学与工程学报，2014，33（1）：14-23.

［3］孙强，张卫强，薛雷，等.砂岩损伤破坏的声发射准平静期特征分析［J］.采矿与安全工程学报，2013，30（2）：237-242.

［4］吴贤振，刘建伟，刘祥鑫，等.岩石声发射振铃累计计数与损伤本构模型的耦合关系探究［J］.采矿与安全工程学报，2015，32（1）：28-41.

［5］李楠，王恩元，赵恩来，等.岩石循环加载和分级加载损伤破坏声发射实验研究［J］.煤炭学报，2010，35（7）：1009-1103.

［6］王述红，徐源，张航，等.岩体损伤破坏过程三维定位声发射试验分析［J］.工程与试验，2010，50（3）：19-23，48.

［7］刘春生，王庆华，李德根.镐型截齿截割阻力谱的分形特征与比能耗模型［J］.煤炭学报，2015，40（11）：2623-2628.

［8］肖福坤，樊慧强，刘刚，等.三轴压缩下含瓦斯煤样破坏过程的声发射特性［J］.黑龙江科技学院学报，2013，23（1）：10-15.

［9］赵洪宝，尹光志.含瓦斯煤声发射特性试验及损伤方程研究［J］.岩土力学，2011，32（3）：667-671.

［10］杨永杰，王德超，郭明福，等.基于三轴压缩声发射试验的岩石损伤特征研究［J］.岩石力学与工程学报，2014，33（1）：98-104.

［11］陈炳瑞，冯夏庭，肖亚勋，等.深埋隧洞TBM施工过程围岩损伤演化声发射试验［J］.岩石力学与工程学报，2010，29（8）：1562-1569.

［12］肖福坤，刘刚，樊慧强，等.瓦斯抽采钻孔煤体破裂过程声发射特性试验研究［J］.煤矿开采，2013，18（2）：7-10.

［13］XIAO FUKUN，LIU GANG.Test of acoustic emission characteristic and COMSOL simulation of coal-body failure in methane drainage bore-hole under complex stress［J］.Electronic Journal of Geotechnical Engineering，2014，15（K）：2367-2378.

（编辑王冬）

Granite damage acoustic emission evaluation

LIU Gang1，ZHANG Yanjun2，SHEN Zhiliang3，WANG Yifei3，YU Han3，LIU Hongwei3
（1.Heilongjiang Ground Pressure&Gas Control in Deep Mining Key Lab，Heilongjiang University of Science& Technology，Harbin 150022，China；2.School of Mechanical Engineering，Heilongjiang University of Science& Technology，Harbin 150022，China；3.School of Mining Engineering，Heilongjiang University of Science&Technology，Harbin 150022，China）

This paper is concerned with an evaluation of the granite crack extension corresponding damage.The evaluation is performed by using the whole stress-strain curve and acoustic emission signal under uniaxial compression of granite sample and applying the AE energy and AE count and stress-strain curve integral gain energy and thereby obtaining data interpolation using the same time theory；deducing the damage evolution equation using fitting curve and performing the quantitative evaluation of the extent to which granite damage occurs under different stress.The experimental results show that there exists consistency between granite macro failure pattern and stress-strain curve peak transition curve；the determination of the three damage stages、early warning，and emergency alarm of brittle granites is accomplished by using the combination of mathematical analytical formula underlying the energy，AE counts and AE energy and damage degree with stress-time curve analysis；and the division of early warning time into 6 ranges is determined by the advantages and disadvantages of characteristic parameters and sensitivity as well as optimizing damage time sensitive effect.The comprehensive analysis shows that AE counts function by giving the first alarm，AE energy works on the second phase，and energy change provides the final judgment of granite instability.

granite；acoustic emission；damage；energy

10.3969/j.issn.2095-7262.2015.06.009

TD315

2095-7262（2015）06-0615-06

A

2015－10－13

国家自然科学基金项目（51574115，51374097）；

刘刚（1986-），男，黑龙江省伊春人，助教，硕士，研究方向：岩石力学，E-mail：18944630110@qq.com。