一种多轴数控机床轮廓误差耦合控制方法*
刘晨希,赵国勇,岳 磊
(山东理工大学机械工程学院,山东淄博 255049)
一种多轴数控机床轮廓误差耦合控制方法*
刘晨希,赵国勇,岳 磊
(山东理工大学机械工程学院,山东淄博 255049)
在分析数控机床传统轮廓误差控制方法不足基础上,提出了一种计算简单、精度高、适合多轴控制的轮廓误差耦合控制方法。该方法包括轮廓误差计算模型和轮廓误差耦合控制方案两部分。提出的轮廓误差计算模型把当前采样周期实际刀具位置到本周期和上一周期插补指令点连线的最短距离近似为轮廓误差;设计的轮廓误差耦合控制方案,实现了对轮廓误差的实时补偿控制。数控仿真加工结果表明所提出轮廓误差耦合控制方法能够有效提高轮廓控制精度。
跟随误差;轮廓误差;耦合控制;轮廓精度
0 引言
轮廓误差补偿技术是提高数控机床轮廓精度的有效途径,因此对轮廓误差补偿控制技术的探索一直是众多学者的研究热点[1-7]。Lo、Chiu设计的切向轮廓误差控制器[8],李宏胜提出的基于模糊自整定控制的交叉耦合控制方案[9],以及赵希梅提出的将ZPETC、ARC、CCC三者结合的控制策略[10],都能在一定程度上提高轮廓误差的控制精度。
在分析传统轮廓误差控制方法计算繁琐、难于加工空间轮廓等不足基础上,本文提出了一种计算简单、精度高、适合多轴控制的轮廓误差耦合控制方法。
1 传统轮廓误差控制算法的不足
数控加工中,轮廓误差一般定义为某采样周期刀具实际位置到指令轨迹的最短距离。对复杂轮廓的数控加工,一般是先用直线段逼近复杂曲线,再用直线插补加工。传统的轮廓误差控制算法把某采样周期刀具的实际位置距指定轨迹在轨迹法线方向上的偏差近似为轮廓误差[1-2],采用的直线轨迹轮廓误差计算模型如图1所示。
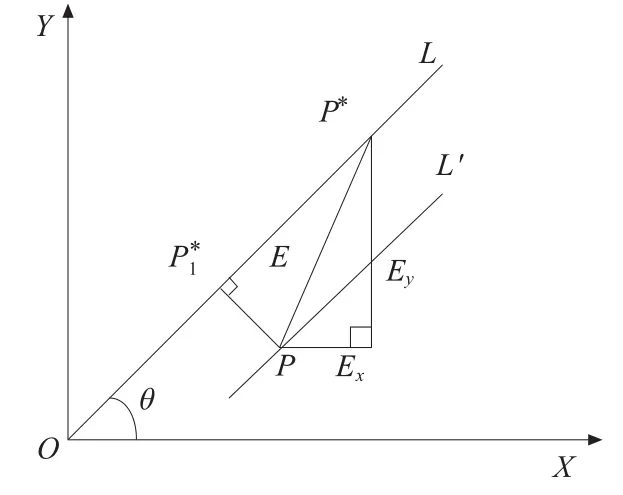
图1 传统轮廓误差计算模型
其中,L为理论加工直线,L′为实际加工直线,设P(Px,Py)为某采样周期刀具实际位置,该时刻指令位置坐标为,Ex和Ey分别是跟随误差在X轴和Y轴的分量,L与X轴的夹角为θ,设垂直于L,轮廓误差ε近似计算如下:
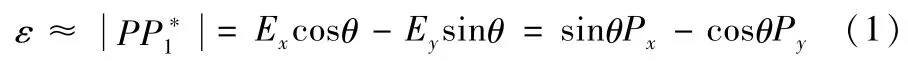
传统的轮廓误差控制算法较适合平面曲线加工,对于曲率变化较大的空间曲线轨迹,则显示出计算繁琐、轮廓误差模型计算精度低等不足。
2 提出的轮廓误差耦合控制方法
提出了一种计算简单、精度高、适合多轴控制的轮廓误差耦合控制方法。该方法包括轮廓误差计算模型和轮廓误差耦合控制方案两部分。
2.1 轮廓误差计算模型
提出的轮廓误差计算模型把当前采样周期实际刀具位置到本周期和上一周期插补指令点连线的最短距离近似为轮廓误差,如图2所示。
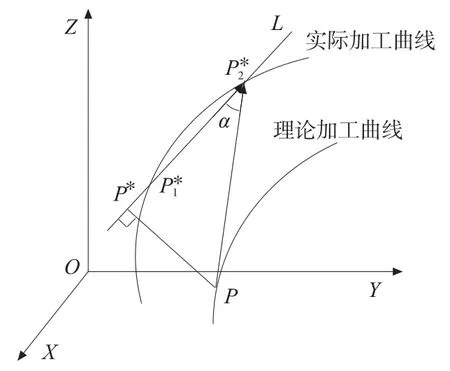
图2 提出的轮廓误差计算模型
设P(Px,Py,Pz)为第k个采样周期刀具实际位置,为第k个采样周期指令插补位置,为第k-1个采样周期的指令插补位置,直线L经过两点,PP*垂直于直线L,与之间的夹角为α,把PP*近似为轮廓误差。
设直线L的方向向量为S,即

则直线L的参数方程可以表示为:

其中,t为参数。
通过P点且垂直于空间直线L的平面的方程为:
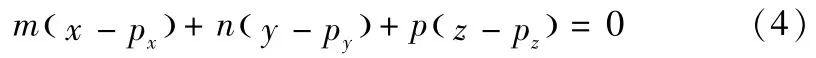
将式(3)代入式(4)得:

即
显然(x,y,z)即为P*点的坐标。轮廓误差在X、Y、Z轴的分量为:
其中:Ex、Ey、Ez分别是跟随误差在X、Y、Z轴的分量。总的轮廓误差为:
这种轮廓误差模型的计算误差始终小于等于插补误差,所以计算精度高。由于轮廓误差是根据空间向量的坐标形式进行计算的,其式(7)结果本身就是各坐标轴的分量,无需再进行解耦处理就可直接应用于轮廓误差补偿控制,因此实时性好。该轮廓误差计算模型适合于直线插补和各种曲线插补场合,通用性好。
2.2 轮廓误差耦合控制方案
提出的轮廓误差耦合控制方案如图3所示,该方案主要由插补器、内存模块、轮廓误差计算模块和各轴位置控制器、执行机构、位置反馈环节等构成。
工作流程如下所述:
(1)将第k-1和第k个采样周期由插补器输出的坐标指令队列同时输出给各轴和系统内存模块。
(2)由系统内存模块的坐标数据和当前插补周期X、Y、Z轴的跟随误差Ex(k),Ey(k),Ez(k)通过式(2)至式(7)即可得到各坐标轴的轮廓误差εx(k)、εy(k)、εz(k)。
(3)将各坐标轴的轮廓误差乘以缩放因子w后分别加到各自轴的跟随误差中,得:
(4)将E′x(k),E′y(k),E′z(k)输入到各自轴的位置控制器计算出向伺服执行机构输出的控制电压量Ux,Uy,Uz。
(5)将控制电压量输出到各轴伺服执行机构来控制系统加工。
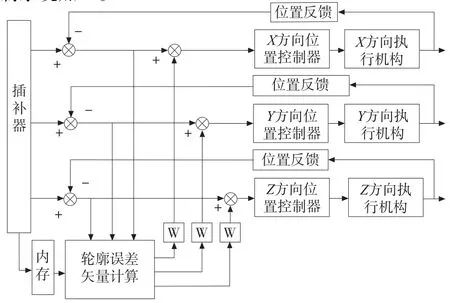
图3 提出的轮廓误差耦合控制方案
3 轮廓误差耦合控制仿真
为了验证所提出轮廓误差耦合控制方法的有效性,对一段空间圆柱螺旋线进行仿真加工。设空间螺旋线底面半径为0.5mm,高度为15mm,导程为1mm。
设机床X、Y、Z向进给系统均采用直流伺服电动机,在不考虑磁场回路电感的情况下可将直流伺服电机的传递函数简化为二阶模型。电机开环传递函数为:

(编辑 李秀敏)
电机开环增益Km=20s-1,磁场回路时间常数Tf=0.0125s,采样时间设为1ms。通过Z—N法整定PID参数,得到PID比例系数、积分时间常数、微分时间常数分别为:Kp=57.6,Ti=0.8,τ=0.0026。
在实际加工中由于电机本身各种参数不完全相同或者其它各种外部干扰的存在,导致各轴动态特性不一致、位置环增益不匹配。所以在PID整定基础上令X、Y、Z轴的磁场回路时间常数和位置环比例系数分别为:Tfx=0.0115s,Kpx=56.6,Tfy=0.0125s,Kpy=57.6,Tfz=0.0135s,Kpz=58.6,来验证所研究的轮廓误差耦合控制方法的有效性。
(1)图4为不采用本文提出的轮廓误差耦合控制方法时的仿真结果,轮廓误差最大值为3μm,平均值为2.8μm。
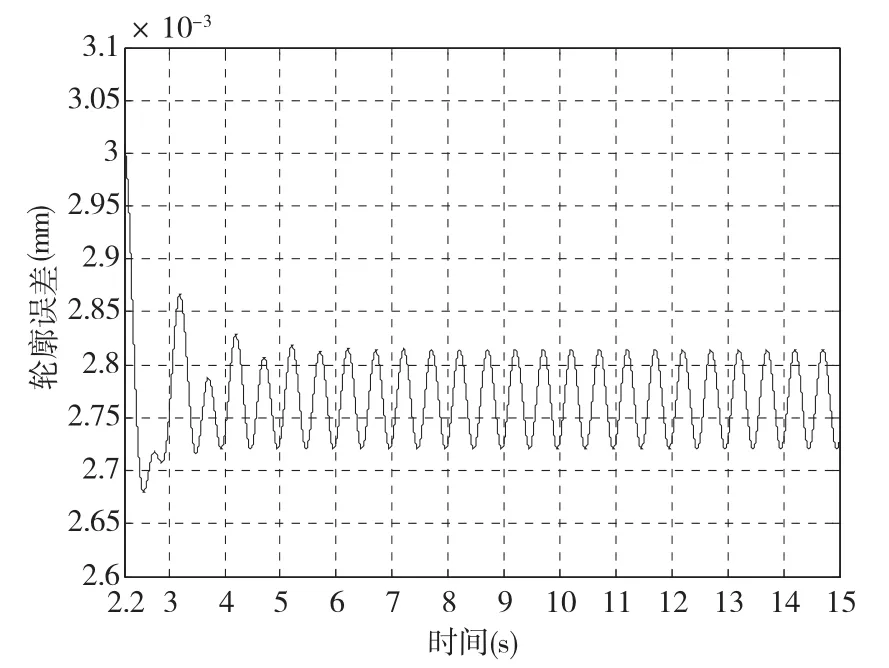
图4 不采用本文提出的轮廓误差耦合控制方法
(2)图5是采用本文提出的轮廓误差耦合控制方法时的仿真结果,采用的轮廓误差缩放因子w为0.9,轮廓误差最大值为0.61μm,平均值为0.56μm。当应用本文提出的轮廓误差耦合控制方法后,轮廓精度提高了近5倍。
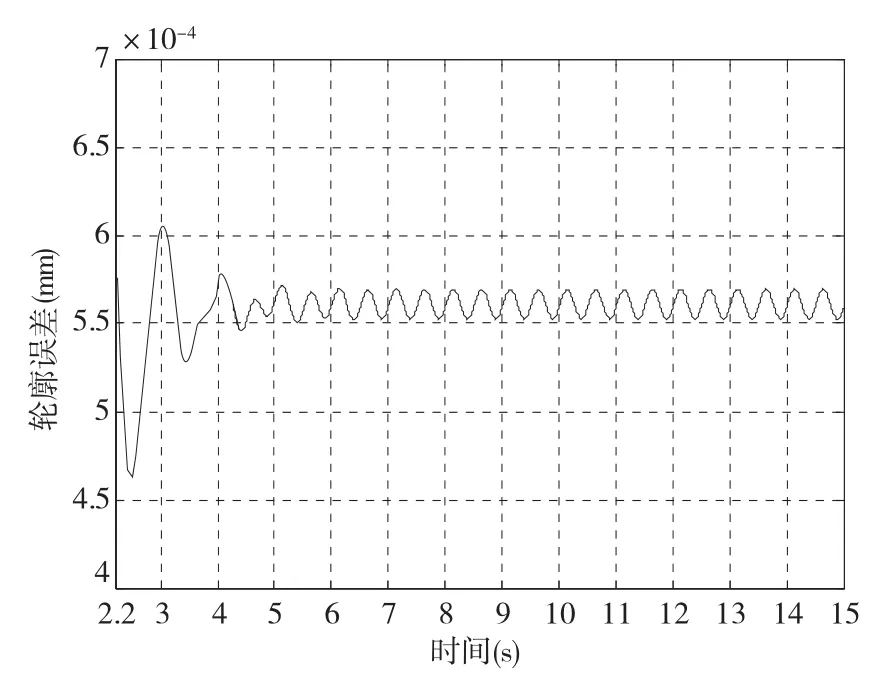
图5 采用本文提出的轮廓误差耦合控制方法
4 结论
提出了一种计算简单、精度高、适合多轴控制的轮廓误差耦合控制方法。该方法包括轮廓误差计算模型和轮廓误差耦合控制方案两部分。仿真结果表明所提出的方法能够有效提高轮廓精度。在以后的研究中,将会把提出的轮廓误差耦合控制方法应用于实际数控机床加工中,以减小各轴动态特性不匹配对轮廓精度的影响。
[1]王广炎,张润孝,帅梅.数控机床的轮廓误差的控制[J].机床与液压,1999(6):59-61.
[2]Myung-Hoon LEE;Seung-Han YANG;Young-Suk KIM;Cheol KIM and Yong-Rae ROH.A Multi-Axis Contour Error Controller for Free Form Curves[J].JSME International Journal.Series C,2004,47(1):144-149.
[3]朱年军,王文,季国顺.数控伺服系统跟踪及轮廓误差分析[J].机床与液压,2006(10):20-21.
[4]孙开珊.多轴空间轮廓误差的建模与交叉耦合控制[D].武汉:华中科技大学,2007.
[5]蔡家斌.两轴运动平台交叉耦合控制系统研究与分析[J].煤矿机械,2008,29(9):50-52.
[6]许强强,曾岳南.两轴变增益交叉耦合控制系统的仿真分析[J].组合机床与自动化加工技术,2010(12):80-82.
[7]孙建仁,胡赤兵,王保民.CNC多轴运动控制系统轮廓误差分析[J].兰州理工大学报,2010,36(4):37-40.
[8]Chen,Chin-Sheng;Chen,LiYeh.Cross-coupling po-sition command shaping control in a multi-axis motion system[J]. Mechatronics,2011,21(3):625-632.
[9]李宏胜.轮廓运动的交叉耦合模糊自整定控制[J].工业仪表与自动化装置,2005(5):18-20.
[10]赵希梅,郭庆鼎.数控机床多轴联动伺服电机的零相位自适应鲁棒交叉耦合控制[J].中国电机工程学报,2008,28(12):129-134.
A Contour Error Coupled Control Approach of Multi-axis CNC Machine Tool
LIU Chen-xi,ZHAO Guo-yong,YUE Lei
(Department of Mechanical Engineering,Shandong University of Technology,Zibo Shandong 255049,China)
On the basis of analyzing the weakness of conventional machine contour control methods,a multi-axis contour error coupled control approach is put forward,which is calculate-simple and high-precision.The developed approach includes contour error calculation model and contour error cross-coupled scheme.The contour error calculation model defines the shortest distance from the actual tool position of current sampling period to the line between the adjacent two interpolation points of the current and the last sampling period,as the contour error.The contour error coupled control scheme can realize real-time contour error compensation.The simulation results show that the developed method is effective to improve CNC machine tool contour accuracy.
tracking error;contour error;coupled control;contour accuracy
TH166;TG659
A
1001-2265(2015)01-0100-03 DOI:10.13462/j.cnki.mmtamt.2015.01.028
2014-05-05;
2014-06-09
国家自然科学基金项目″五轴联动数控机床轮廓误差耦合控制理论与方法研究″(51105236)
刘晨希(1989—),男,山东临沂人,山东理工大学硕士研究生,研究方向为数控技术与装备;通讯作者:赵国勇(1976—),男,山东淄博人,山东理工大学副教授,博士,研究方向为机械制造自动化技术,(E-mail)zgy709@126.com。

