基于GA与RBF神经网络的工程陶瓷点磨削表面硬度数值模拟*
马廉洁,曹小兵,陈小辉,李 琛
(1.东北大学秦皇岛分校控制工程学院,河北 秦皇岛 066004;2.东北大学 机械工程与自动化学院,沈阳 110819)
基于GA与RBF神经网络的工程陶瓷点磨削表面硬度数值模拟*
马廉洁1,2,曹小兵1,陈小辉1,李 琛1
(1.东北大学秦皇岛分校控制工程学院,河北 秦皇岛 066004;2.东北大学 机械工程与自动化学院,沈阳 110819)
基于RBF神经网络理论,对工程陶瓷点磨削表面硬度HV与切削速度vc、进给速度f、切削深度ap、倾斜角α、和偏转角β五个工艺参数的关系进行了单因素数值拟合,并以拟合优度对拟合结果进行了检验,检验结果表明模型具有较高可信度。基于遗传优化算法,对点磨削表面硬度关于五个工艺参数的多元模型进行了优化建模,设计了正交实验对模型进行检验,最大误差在10%以内,表明模型具有较高的可靠性。
表面硬度;数值模拟;遗传算法;RBF神经网络;点磨削;工程陶瓷
0 引言
氟金云母陶瓷是一种典型工程陶瓷,具有优良的机械性能、抗冲击性、热震性,兼具无机非金属材料的物理和化学性能[1-2],在国防、航空航天、精密仪器等尖端领域有着十分广阔的应用前景[2-4]。点磨削是一项高效磨削加工技术,它兼具磨削的高表面质量和车削的高生产率[5-6],为工程陶瓷加工制造提供了一种优质加工工艺。研究工程陶瓷加工表面完整性,获取高精密的加工精度和表面质量,是工程陶瓷材料获得广泛应用的重要前提[2-4],而表面硬度作为衡量表面完整性的重要指标,研究点磨削表面硬度与工艺参数的关系,对工程陶瓷加工表面质量的提高具有重要的理论指导意义。
遗传算法[7-8](Genetic Algorithms,GA)是一种仿生智能优化算法,能够有效地避免传统优化方法存在的微分问题,在求解不可导、非连续及高维极值等方面得到了广泛应用[8];径向基神经网络(Radial Basis Function,RBF)是一种三层前向型网络,具有训练速度快、结构简单、泛化能力强等特性,在数据挖掘、数值模拟、函数预测等领域得到了广泛应用[9-10]。
本文以氟金云母陶瓷点磨削加工实验为基础,建立了RBF神经网络预测模型,通过单因素数值拟合,研究了点磨削表面硬度分别与切削速度vc、进给速度f、切削深度ap、倾斜角α及偏转角β的关系,利用遗传算法对点磨削表面硬度关于五个工艺参数的多元模型进行了优化建模,并检验了模型的可靠性。
1 RBF神经网络理论
径向基神经网络(Radial Basis Function,RBF)是一种三层前向型网络,分别为输入层、隐含层、输出层,其基本神经元结构如图1所示,各邻层之间以权值连接,隐含层节点通过核函数实现一种非线性变化,将输入空间映射一个新空间,输出层节点在新空间实现线性加权组合。
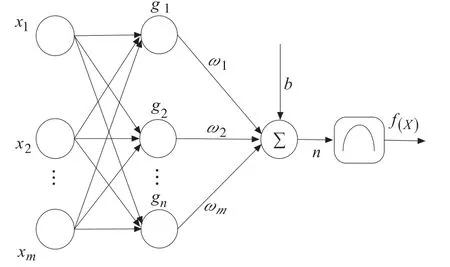
图1 RBF神经元网络结构图
设输入向量为X(x1,x2,···,xi),则RBF神经元网络结构可描述为:
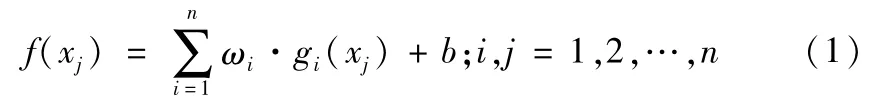
式(1)中ωi为隐含层与输出层之间的权值,n为隐层节点的个数,xj为第j个输入值,gi(xj)为第j个径向基核函数,取高斯径向基核函数:

式(2)中ci为第i个核函数中心,为第i个核函数的宽度,为欧几里得范数。
2 基于RBF网络的单因素数值拟合
2.1 表面硬度HV与切削速度vc的关系
基于实验值与RBF神经网络预测值(图2),在vc∈(20,70)区间内(单位:m/s),随切削速度的增大,表面硬度变化趋势为先下降后上升,提出假设模型模型(3),经数值拟合,得解析式(式(4)),模型拟合优度R=0.9813,表明模型具有较高的可信度。
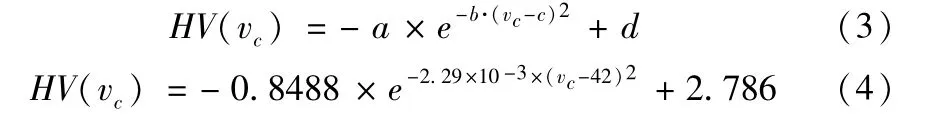
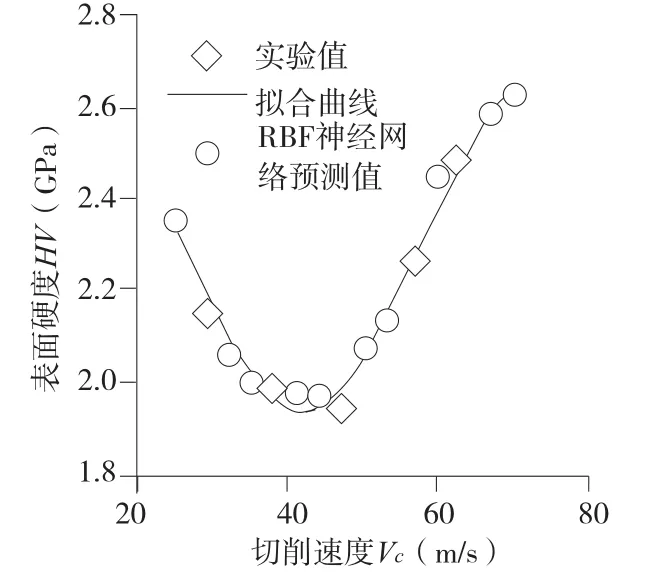
图2 表面硬度与切削速度的关系
2.2 表面硬度HV与进给速度f的关系
基于实验值与RBF神经网络预测值(图3),在f∈(10,80)区间内(单位:mm/min),随着进给速度f的增加,表面硬度总体变化趋势为先下降后上升,提出假设模型(式(5)),经数值拟合,得解析式(式(6)),模型拟合优度R=0.8552,表明模型具有一定可信度。

图3 进给速度对表面硬度的关系

2.3 表面硬度HV与切削深度ap的关系
观察实验值与神经网络预测值的变化趋势(图4),提出模型(式(7)),经数值拟合,得解析式(式(8)),模型拟合优度R=0.8152,表明模型具有一定可信度。

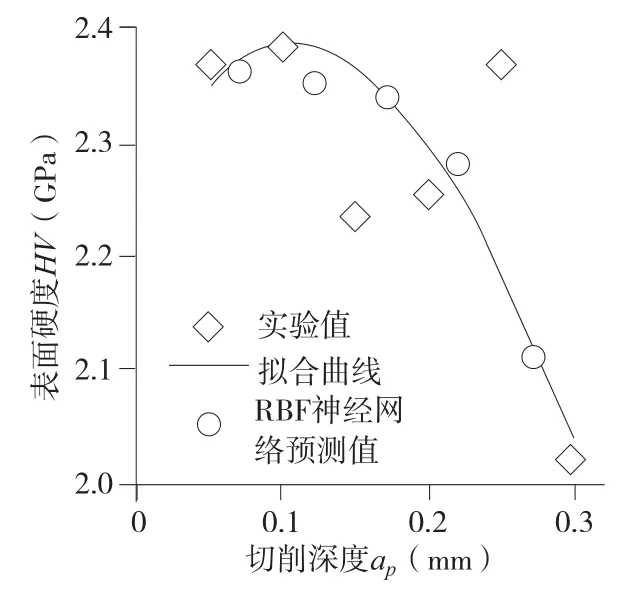
图4 切削深度对表面硬度的关系
2.4 表面硬度HV与倾斜角α的关系
基于实验值与RBF神经网络预测值(图5),当倾斜角α增大时,考查表面硬度的变化趋势呈现正弦变化,但考虑到振幅的变化,在振幅处添加了修正项,提出假设模型(式(9)),经数值拟合,得解析式(式(10)),拟合优度R=0.9652,表明模型具有较高的可信度。
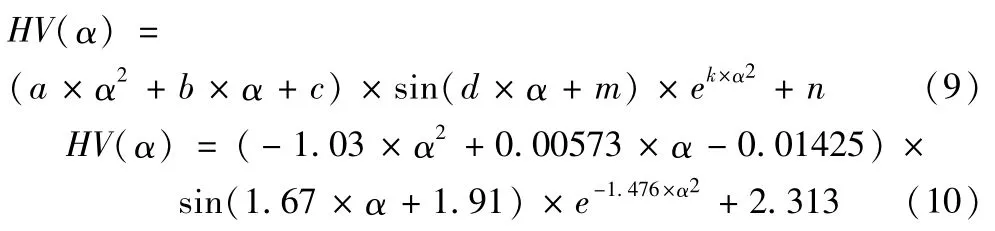
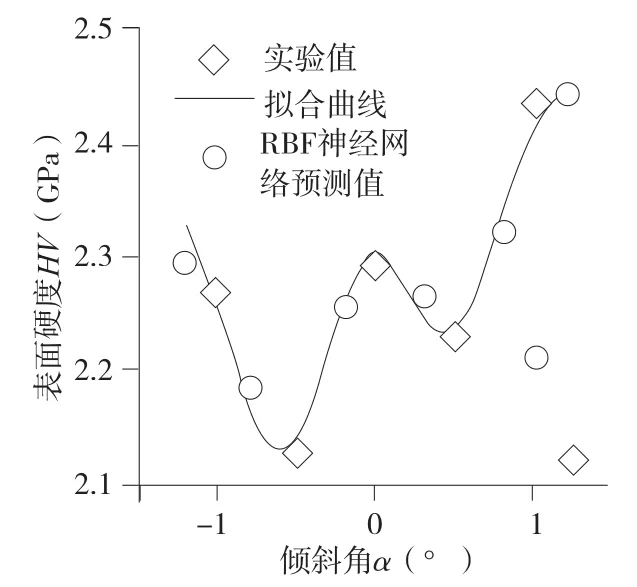
图5 倾斜角α对表面硬度的关系
2.5 表面硬度HV与偏转角β的关系
基于实验数据与神经网络预测值(图6),在β∈(-3,6)区间内,当偏转角β增大时,表面硬度呈现先下降后上升趋势,提出假设模型(式(11)),经数值拟合,得解析式(式(12)),拟合优度R=0.9498,表明模型具有较高可信度。

图6 偏转角β对表面硬度的关系
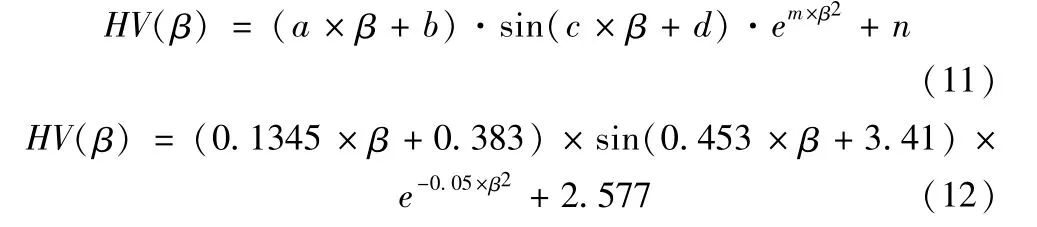
3 基于遗传算法的模型优化求解与检验
3.1 遗传算法原理
遗传算法(Genetic Algorithms,GA)是一种基于生物遗传与进化机制的仿生智能优化算法,效仿了自然选择遗传过程中的选择、交叉、变异等现象。遗传算法把问题参数编码为染色体,利用选择、交叉、变异等操作使种群的染色体进化到搜索空间中越来越好的区域,最终收敛符合优化目标的染色体。算法流程图如图7所示,具体步骤如下:
(1)编码,将待解问题编码成编码串,并随机生成初始种群;
(2)选取适应度函数,将待解问题目标函数转化成适应度;
(3)选择、交叉及变异,根据适应度函数,选取父代,遗传进化得到子代种群;
(4)重复步骤2~3,直到满足预先设定的停止准则为止;
(5)通过一代一代的迭代进化,得到最适应待解问题的个体,即最终收敛结果。

图7 遗传算法流程图
3.2 模型假设
基于单因素数值拟合的结果(式(4)、(6)、(8)、(10)、(12)),提出了点磨削表面硬度关于工艺参数的多元模型(式(13)),模型由四部分组成,观察式(8)、式(10)和式(12),考查它们的共同项,均含有二次或一次函数项,提出模型的第一项(a1×(apαβ)2+a2×apαβ+ a3);模型的第二项为正弦函数项,而只有式(10)和式(12)含有正弦项,故提出模型的第二项sin(b1×αβ+ b2),此项包含工艺参数α,β;模型的第三项为以欧拉数为底数的指数项,综合考查单因素数值拟合的结果,发现各工艺参数与表面硬度均呈现指数关系,故提出模型的第四项;模型的第四项为一常数。
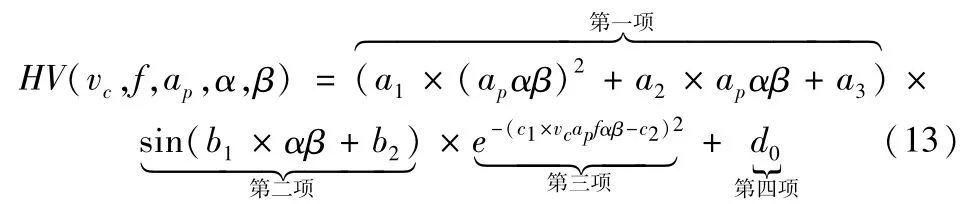
式(13)中a1,a2,a3,b1,b2,c1,c2,d0均为常数,其具体取值与刀具与工件的材料属性有关。
3.3 实验
本文采用正交设计优化实验方案(如表1所示,A—vc(m/s),B—f(mm/min),C—ap(mm),D—α(°),E—β(°)),对多元模型式(13)进行优化建模,正交实验结果如表2所示。以12组正交实验(第1,3,4,5,7,8,9,11,12,13,15,16组)进行多因素数值模拟,以多元模型与正交实验结果的方差最小为适应度准则(式(14)),利用遗传算法进行优化求解,以4组正交实验结果(第2,6,10,14组)对所解模型进行验证。
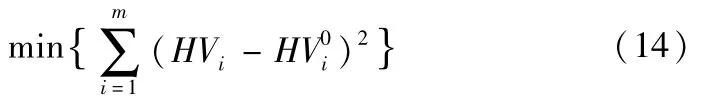
式(14)中HVi为多元模型值(式(13)),为实验值,m为用于优化的实验组数。
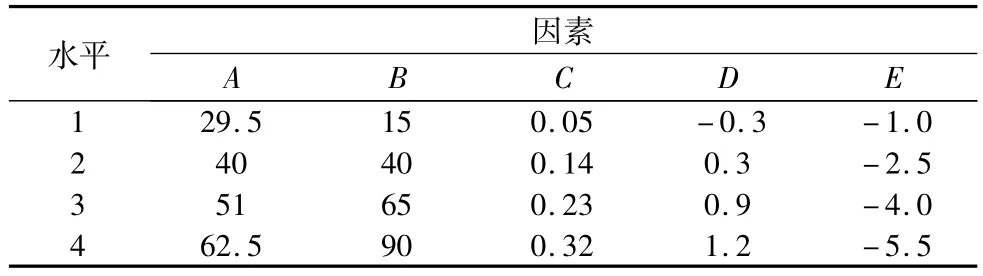
表1 正交实验因素水平表
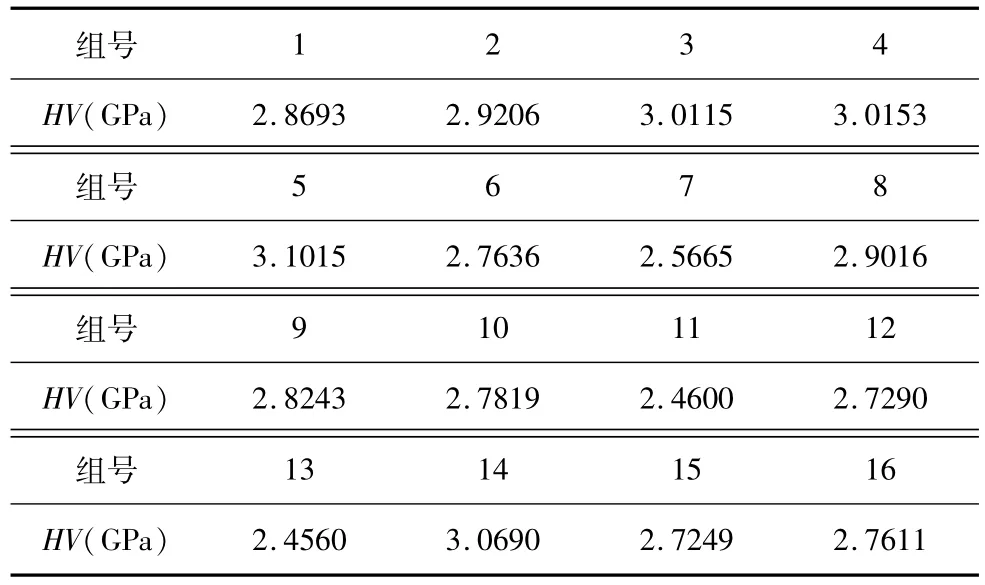
表2 正交实验结果
3.4 结果与检验
基于遗传算法优化的最优个体适应度函数值变化曲线如图8所示,反应了参数(a1,a2,a3,b1,b2,c1,c2,d0)的解的变化过程,所得优化参数解如表3所示,基于遗传算法优化的表面硬度多元模型如式(15)所示。利用4组正交实验对多元模型进行了验证,检验结果如表4所示,误差均在10%以内。通过实验值与多元模型值的比较(图9),可知模型在定量上与实验值存在着一定误差,但能够定性地反映出表面硬度的变化趋势,考虑到点磨削加工过程的复杂性,影响因素众多,此误差区间可以接受,模型具有一定的可靠性。


图8 最优个体适应度函数变化曲线

图9 实验值与模型值

表3 参数表

表4 误差表
4 结论
(1)基于实验数据与RBF神经网络预测数据,通过最小二乘一元回归进行了单因素数值拟合,得到了表面硬度HV分别与切削速度vc、进给速度f、切削速度ap、倾斜角α和偏转角β的关系式,拟合优度检验表明模型具有较高的精度,在定性上能够较好地反映出点磨削表明硬度的变化趋势。
(2)基于遗传优化算法,建立了点磨削表面硬度关于工艺参数的多元模型,并检验了模型的可靠性,结果表明,模型能够较好地反映出表面硬度与五个工艺参数之间的关系,模型具有较高的可靠性。
[1]Boccaccini A R.Machinablity and brittleness of glass-ceramic[J].J Mater Process.Technol,1997,65(1-3):302-304.
[2]郑治,黄伯云,谭彦妮,等.羟基磷灰石/氟金云母复合的生物玻璃陶瓷的力学性能[J].中南大学学报(自然科学版),2009,40(3):638-643.
[3]Taruta S,Hayadhi T,Kitajimak.Preparation of machinable cordierite/mica-composite by low-temperature sintering[J]. J.Eur.Ceram.Soc,2004,24(10-11):3149-3154.
[4]Mustafa E A A.Fluorophlogopite porcelain based on talcfeldspar mixture[J].Ceramics international,2001,27(1):9-14.
[5]巩亚东,仇健,李晓,等.超高速点磨削相关机理研究[J].机械工程学报,2010,46(17):172-178.
[6]巩亚东,曹振轩,刘月明,等.高速点磨削参数对温度场与表面硬度的影响[J].东北大学学报(自然科学版),2012,33(3):414-417.
[7]Holland J H.Adaptation in natural and artificial systems:An introductory analysis with applications to biology,control,and artificial intelligence[M].U Michigan Press,1975.
[8]张铃,张钹.遗传算法机理的研究[J].软件学报,2000,11(7):945-952.
[9]Park J,Sandberg IW.Universal approximation using radialbasis-function networks[J].Neural computation,1991,3(2):246-257.
[10]柴杰,江青茵.RBF神经网络的函数逼近能力及其算法[J].模式识别与人工智能,2002,15(3):310-316.
(编辑 李秀敏)
Numerical Simulation of Surface Hardness Based on GA and RBF Neural Network in Point Grinding Engineering Ceramic
MA Lian-jie1,2,CAO Xiao-bing1,CHEN Xiao-hui1,LI Chen1
(1.School of Control Engineering,Northeastern University at Qinhuangdao,Qinhuangdao Hebei066004,China;2.School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,China)
Inpoint grinding engineering ceramic,the relationship between surface hardness HV and cutting speed vc,feed speed f,cutting depth ap,inclining angleαanddeflecting angleβwere univariate numerical fitting based on RBF neural network.Andfitting resultsare tested by the coefficient of determination,test results show that the model has high credibility.Amultivariate modelissolvedbetween surface hardness with fiveprocess parametersbased on genetic optimization algorithmin point grinding.The orthogonal experiment was designed to test the model,the maximum error is less than 10%.The results indicated that the model has high reliability.
surface hardness;numerical simulation;genetic algorithms;RBF neural network;point grinding;engineering ceramics
TH161;TG506
A
1001-2265(2015)01-0030-04 DOI:10.13462/j.cnki.mmtamt.2015.01.009
2014-04-17
国家自然科学基金项目资助(51275083)
马廉洁(1970—),男,内蒙古赤峰人,东北大学副教授,博士,硕士生导师,研究方向为硬脆材料加工理论与技术,(E-mail)mlj@mail. neu.edu.cn。

