基于排队理论的云计算中心性能分析模型
廖倩文,潘久辉,王开杰
(暨南大学信息科学技术学院,广州510632)
基于排队理论的云计算中心性能分析模型
廖倩文,潘久辉,王开杰
(暨南大学信息科学技术学院,广州510632)
为全面、客观分析云计算系统中心的性能,提出一种改进的云计算中心系统分析模型。利用泊松分布描述批量到达云计算中心的用户服务请求变化特点,建立基于排队论的批量到达系统模型,在概率空间上求解队长的稳态概率,采用仿真实验对阻塞概率、立即服务概率等性能指标进行分析。仿真结果表明,随着批量到达请求数增加,云计算中心的平均队长相应增加,降低了系统的阻塞概率。
云计算系统;性能分析;排队论;平均等待队长;批量到达
1 概述
云计算系统是一种以互联网为核心的数据处理中心,对存储、软件、服务等资源进行统一调度,构成一个虚拟计算机中心,为用户提供按需服务的商业模式[1-2]。由于用户需求的种数不断增加,用户对云计算系统中心的服务质量提出更高的要求[3]。云计算中心是云计算系统的核心,其性能的优劣直接决定了云计算服务质量的优劣,因此对云计算系统中心的性能进行全面、准确分析具有十分重要的意义[4]。
针对云计算系统中心的性能分析问题,国内外学者、专家投入了大量的时间、精力进行广泛的研究,涌现了许多云计算中心的性能模型[5]。传统云计算系统中心性能分析模型采用模拟仿真系统如CloudSim实现[6],它们属于类静态分析模型,假设云计算系统中心是一种静态的工作状态,然而,在实际应用中,云计算系统中心规模庞大、结构复杂,具有时变性和突变性,传统模型难以建立准确的性能分析模型[7]。为了解决传统模型存在的不足,文献[8]提出了基于数据聚集算法的云计算系统中心分析模型,在考虑服务质量基础上降低系统能耗;文献[9]提出了性能受限的云中心异构服务器能耗优化模型,解决了云计算中心资源配置不合理等难题。近些年,随着排队理论的不断发展,一些学者将其引入到云计算系统中心性能分析中,文献[10]提出了基于利润最大化的云计算系统中心性能分析方法,将多服务器的云计算中心优化问题看作为一个M/M/m排队问题,根据利润最大化得到最优优化方案;文献[11]提出了基于M/M/l的排队系统云计算中心性能分析模型,提高了服务的响应时间,降低了中心的能耗;文献[12]提出了基于M/G/m/m+r排队论的云计算中心性能分析模型。
为了更加准确、全面对云计算系统中心性能进行分析,本文提出一种基于排队理论的批量到达云计算中心性能分析模型。将用户服务请求过程看作为是一个参数为λ的泊松流,而且每批用户服务请求数的概率分布已知,从而建立了云计算中心性能分析模型,然后给出系统稳态运行指标的计算方法,最后通过仿真实验对模型的有效性和优越性进行测试。
2 云计算中心的工作机制和排队模型
2.1 云计算中心的工作机制
在云计算系统中,通常有大批用户服务请求进入数据处理中心。由于中心有不同类型的服务台,一旦有用户服务需求到来时,云计算中心根据用户的需求自适应提供不同类型的服务,不同类型服务的价格不一样,云计算系统中心的工作机制如图1所示[13]。

图1 云计算中心的工作机制
2.2 云计算中心的排队模型
排队系统是运筹学的重要分支,又称为随机服务系统,通过排队等待中的概率处理最优化设计问题,其成功应用于通信系统、生产管理系统等[14]。排队系统包括到达过程、排队规则、服务机制,对于云计算中心性能优化问题,具体假设如下:
(1)用户服务请求到达云计算系统的中心是随机的,用户服务请求批与批之间到达时间的间隔服从参数为λ的泊松流,用户服务请求所需的服务时间均服从参数μ的负指数分布。
(2)每批用户服务请求的数目为一个随机变量ξ,其概率分布为:P(ξ=i)=αi,i=1,2,…,K。
(3)云计算中心有m个服务台(m<K),每一个服务台独立工作,在不同批次到达的用户服务请求中,服务顺序按先到先服务(First Come First Server,FCFS)的规则。
(4)云计算系统中心的容量有限,即系统中心最多可以容纳m个用户服务请求,如果云计算系统中心的容量已满,那么新到达的用户服务请求便离去,另寻服务,不然就需要进行排队等待[15]。
云计算中心的排队模型如图2所示。

图2 云计算中心的排队模型
3 云计算系统中心的性能分析模型
3.1 马尔可夫链
马尔可夫过程是指在已知某一随机过程现在的条件下,“将来”与“过去”是独立的,马尔可夫链是一个时间与状态都离散的时间序列。若随机过程{X(t),t∈T}满足:
(1)状态空间S为R的马尔可夫链。
(2)任n≥1,t1<t2<…<tn,如果式(1)成立,那么称{X(t),t∈T}为马尔可夫链。

设I为马尔可夫链{Xn,n≥0}的状态空间,那么条件概率为:

根据每个预测对象的具体情况,将状态空间划分成若干区域,每个区域构成一个状态,设任一状态记为Ei∈(E1i,E2i],i=1,2,…,s,s为状态数目,E1i和E2i分别为第i种状态的上下界,那么状态转移概率矩阵公式为:

得到状态转移概率矩阵的计算公式为:

3.2 云计算中心性能分析模型的建立
设X(t)表示t时刻云计算中心的用户服务请求数),根据排队论可以知道,云计算中心的状态空间为E=(0,1,…,m),云计算中心的状态转移过程如图3所示。
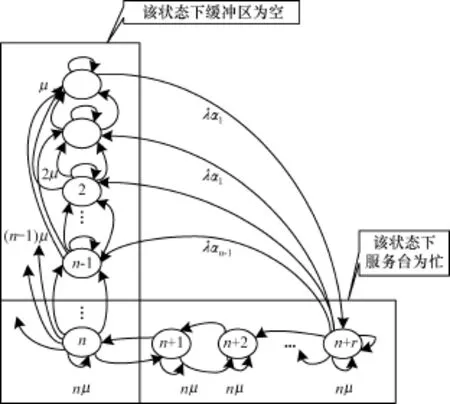
图3 云计算中心的状态转移过程
云计算中心的状态转移满足如下规则:
(1)任意一个状态i向右可以到达其后状态:i+ 1,i+2,…,i+K,向左可以到达自身的相邻状态i-1。
(2)任意一个状态i可以向左达到任意一个状态i-K,…,i-2,i-1,而右边状态中,只有状态i+1可到状态i。
(3)以状态n为分界点,左边和右边的状态i(0<i<n)转移率分别为iμ和nμ。
由于图3是一个有限状态马尔可夫过程,其存在平稳分布,根据由概率守恒原理得到稳态方程组:

根据式(5)进行求解,可得到系统稳态概率分布P0,P1,…,Pm,然后可以计算出队长概率Pi的值。
4 仿真实验
4.1 仿真环境
为了测试基于排队论的云计算系统中心性能分析模型的有效性和优越性,在Intel(R)Dual Core(TM)3.0 GHz CPU,4 GB RAM,W indows XP操作系统的计算机上,采用Matlab 2013进行仿真实验,相关参数如表1所示。

表1 仿真实验参数设置
4.2 性能评价指标
为了对云计算中心的性能进行客观和准确评价,本文选择系统请求总数、阻塞概率、立即服务概率、平均队长作为模型性能评价指标,它们分别定义如下:

4.3 结果与分析
性能指标分析如下:
(1)系统请求总数
系统请求总数的变化曲线如图4所示,从图4可以看出,随着输入队列缓冲区长度增加,当服务节点数m=100时,系统请求总数的增长比较平缓,当m=500时,根本看不出队列缓冲区大小对系统请求总数的影响。

图4 系统请求数
(2)阻塞概率
阻塞概率变化曲线如图5所示。从图5可以明显的看出,随着输入队列缓冲区的增加,阻塞概率大幅度下降,在系统阻塞概率小于0.2%条件下,输入队列缓冲区长度应该为服务节点数的10%,即当n= 100时,系统输入队列缓冲区长度最小值应该10,当增加缓冲区长度时,系统阻塞概率会下降,可以提高了系统的运行效率,但是增加到一定程度时,系统阻塞概率处于稳定状态。

图5 阻塞概率
(3)立即服务概率
立即服务概率是指用户请求服务无须任何排队等待就可以获得服务的概率,是评价云计算系统中心服务性能的一个关键指标。立即服务概率变化曲线如图6所示。从图6可以看出,随着输入队列缓冲区长度增加,立即服务概率下降,这意味着当输入队列缓冲区的长度较小时,到达云计算系统中心的请求可以获得立即服务,不需要进入排队等待。同时,从图6(c)看出,服务节点数越多,立即服务概率就越高,系统的性能就越好。
(4)平均队长的分析
平均队长的变化曲线如图7所示。从图7可知,随着批量用户请求服务数的增多,平均队长不断增加,到达一定的数量后,又慢慢开始减少,这主要是由于批量用户请求服务数增加,占据大量的队列缓冲区,后面的用户请求服务不能进入队列缓冲区而寻服务,等用户请求服务得到满足后,平均队长又逐渐减少。

图6 立即服务概率
5 结束语
为对云计算系统中心的性能进行描述,本文提出基于排队论的云计算中心性能分析模型,仿真结果表明,当批量到达请求数增加时,云中心平均队长不断增加,增加云计算系统的缓冲区长度,可降低系统的阻塞概率,而且服务节点数越多,立即服务概率就越高,实验结果可以为云中心的资源配置和参数调整提供较好的参考意见,具有一定的实用价值。

图7 平均队长
[1] 过敏意.绿色计算:内涵及趋势[J].计算机工程,2010,36(10):1-7.
[2] 王 珊,王会举,覃雄派,等.架构大数据:挑战、现状与展望[J].计算机学报,2011,34(10):1742-1747.
[3] 冻 康,郑纬民.云计算:系统实例与研究现状[J].软件学报,2009,20(5):1337-1340.
[4] 史佩昌,王怀民,蒋 杰,等.面向云计算的网络化平台研究与实现[J].计算机工程与科学,2009,31(z1):249-252.
[5] 许 丞,刘 洪,谭 良.Hadoop云平台的一种新的任务调度和监控机制[J].计算机科学,2013,40(1):112-117.
[6] 李春艳,何一舟,戴 彬.Hadoop平台的多队列作业调度优化方法研究[J].计算机应用研究,2014,31(3):705-708.
[7] 王意洁,孙伟东,周 松,等.云计算环境下的分布存储关键技术[J].软件学报,2012,23(4):962-986.
[8] 徐小龙,杨 庚,李玲娟,等.面向绿色云计算数据中心的动态数据聚集算法[J].系统工程与电子技术,2012,34(9):1927-1934.
[9] 何怀文,傅 瑜,杨 亮,等.性能受限下云中心异构服务器的能耗优化[J].计算机应用,2009,20(5):1337-1340.
[10] 王 巍,罗军舟,宋爱波.基于动态定价策略的数据中心能耗成本优化[J].计算机学报,2013,36(3):599-612.
[11] Khazaei H,M isic J,M isic V B.Performance Analysis of Cloud Computing Centers Using M/G/m/m+r Queuing Systems[J].IEEE Transactions on Parallel and Distributed System s,2012,23(5):936-943.
[12] Guo Liheng,Yan Tao,Zhao Shuguang,et al.dynamic Performance Optimization for Cloud Computing Using M/M/m Queuing System[J].Journal of Applied Mathematics,2014,24(12):2429-2438.
[13] Khazaei H,Misic J,Misic V B.Performance of Cloud Centers with High Degree of Virtualization Under Batch Task Arrivals[J].Parallel and Distributed System s,2013,24(12):2429-2438.
[14] 邱国新,姜海波.批量到达的M(ξ)/G/n/m多服务台排队系统研究[J].甘肃科学学报,2013,25(1):120-123.
[15] 何怀文,傅 瑜,杨毅红,等.基于M/M/n/n+r排队模型的云计算中心服务性能分析[J].计算机应用,2014,34(7):1843-1847.
编辑 索书志
Per form ance Analysis Model of C loud Computing Center Based on Queuing Theory
LIAO Qianwen,PAN Jiuhui,WANG Kaijie
(College of Information Science and Technology,Jinan University,Guangzhou 510632,China)
In order to com prehensively and objectively analyse the performance for cloud computing system s center,this paper presents a performance analysis model of cloud Computing center based on queuing theory.The characteristics of the user service request which reaches the center are described and a the system model for batch arrivals by using queuing theory is established,and the length of steady-state probability is solved in probability space.Finally,the simulation experiments are carried out to test the performance by using blocking probability,immediate service probability,etc. Simulation results show that,With the increase of the number of batch arrival request,average length of cloud Computing center increases,and increasing the buffer length can reduce the blocking probability.
cloud computing system;performance analysis;queuing theory;mean waiting queue size;batch arrivals
廖倩文,潘久辉,王开杰.基于排队理论的云计算中心性能分析模型[J].计算机工程,2015,41(9):51-55.
英文引用格式:Liao Qianwen,Pan Jiuhui,Wang Kaijie.Performance Analysis Model of Cloud Computing Center Based on Queuing Theory[J].Computer Engineering,2015,41(9):51-55.
1000-3428(2015)09-0051-05
A
TP393
10.3969/j.issn.1000-3428.2015.09.009
武汉大学软件工程国家重点实验室开放基金资助项目(SKLSE2012-09-37);公安部技术研究计划基金资助项目(2014 JSYJB048)。
廖倩文(1989-),男,硕士研究生,主研方向:信息集成,数据质量管理;潘久辉,教授、博士生导师;王开杰,硕士研究生。
2014-12-26
2015-02-11 E-m ail:liaoqianw en_77@163.com

