舰船瞬态信号判别方法

经验人：孙 嵘

舰船瞬态信号判别方法

经验人：孙 嵘

为了实现舰船瞬态信号的分析与评价，首先要解决的是信号的有无、在哪等问题，为此本文拟通过瞬态信号检测的方式来解决这一问题。传统的瞬态信号检测的方式多采用能量判别，即依据瞬态信号的“跳跃”特征进行判断，但是这一方法仅能判断信号的跳变而无法判断是否来源于舰船，基于此原因，本文基于似然函数比，利用信号匹配的方式，寻找最优样本函数，然后对最优结果进行似然比对，以似然函数最高者为判别输出，仿真研究结果表明，该方法可以较好地判别瞬态信号的产生时刻和结束时刻。

舰船瞬态信号判别方法的实现

假设海洋环境噪声服从高斯分布，在这一条件下的舰船瞬态噪声的检测问题主要是从舰船辐射噪声N 点 DFT数据中获取任意 M 点信号，该信号即为瞬态信号在辐射噪声谱中所占的成分。由于瞬态信号的强弱程度未知，因此对这类似于检测未知谱形状的信号，学者Nuttal 提出了以下非参量 Power-Law 检测方法，该方法基本原理是将获取的舰船辐射噪声时域信号中每间隔 N 个点分成一段，然后依次对每段数据利用（1）式进行判别是否存在“跃变”信号。

上式中，Xk为舰船辐射信号x（t）的DFT计算结果中第k个点幅度的平方，即

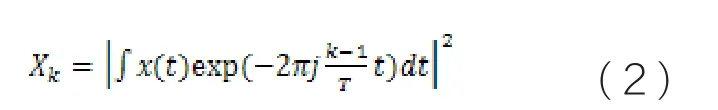
（2）式中 T 为整段信号的积分时间，m 为非负实数。经反复试验验证，学者Nuttal 提出 m = 2.5时瞬态信号的检测性能最佳。因此，该方法的检测统计量仅是周期图谱值 m 次方的和，其不需要任何与待检测信号相关的先验知识，说明这一方法对舰船噪声的先验认识依赖程度很低。

此外，上面阐述的 Power-Law 检测方法需要对待检数据首先进行预白化处理，为了克服这一局限性，Nuttal提出了不需要预白化的恒虚警检测表达式如下：

仿真研究

仿真算例1：100s的均值为0，方差为1的高斯白噪声信号noise，作为信号的主要成分。根据信噪比的公式有

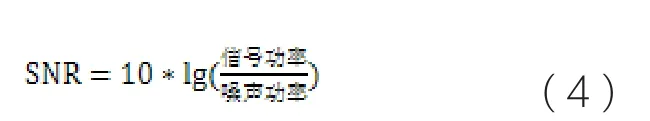
SNR为仿真信号的信噪比。噪声功率是指白噪声功率，即为白噪声的方差，为1。由此可以计算出信号的功率。以最简单的正弦信号为例，信号为，采样率为8000HZ，可以计算出信号的幅值A，最终得到的信号为

为了更好的说明Power-Law检测器的性质，x（t）取得时间长度为2s，大于实际瞬态噪声的时间长度。

图1给出了典型瞬态信号时域波形图，由图可见，瞬态噪声在中间时刻出现并呈现幅值随时间逐渐衰减的趋势。

先来讨论两种极端情况。当瞬态信号的初始幅值很大时，极限情况为无穷大，根据信号比的公式，则此时此瞬态信号的信噪比为无穷大；当瞬态信号的幅值衰减到很小时，极限情况为0，则根据信噪比公式信号的信噪比为无穷小。瞬态信号是时间非常短的信号，短时间内信号的幅值就从极大衰减到极小，故无法说明检测器在不同信噪比下的检测性能，因此用短时间的稳态信号来代替瞬态信号进行检测，可以很好的反应出该检测器在不同信噪比下的检测性能。

本文在信号的信噪比分别是10dB、5dB、0dB、-5dB、-8dB和-10dB的情况下（这里信噪比大小是通过瞬态信号和混合局部时间段信号的方差来确定），对检测器的性能进行了仿真，仿真结果如图2-图7所示。每幅图都分为上、中、下三幅小图，分别为信号的时域图、检测器仿真结果图和仿真结果的局部放大图。图中的最上面小图的时域信号中，采样频率为8000HZ，信号的长度为100s，其中50s至52s的时间是仿真的瞬态信号和白噪声信号的叠加。检测器的窗长度为信号长度的1/100，窗口重叠率为50％。

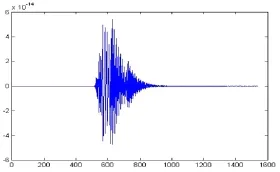
图1　典型瞬态信号时域波形

由图2至图7可以看出，在信号的信噪比很好的情况下，该检测器可以很好的检测出信号的出现时刻和持续时间。当信噪比逐渐降低时，检测器的性能开始逐渐下降，但是在信噪比为0dB甚至是-5dB时，仍能很好的对信号进行检测。当信号的信噪比进一步降低时，检测器的性能明显出现了不足，当信噪比降低为-8dB时，检测器的检测性能已经非常微弱，而当信噪比进一步降低为-10dB时，检测器完全失效，不能检测出该信号的出现时刻和持续时间。

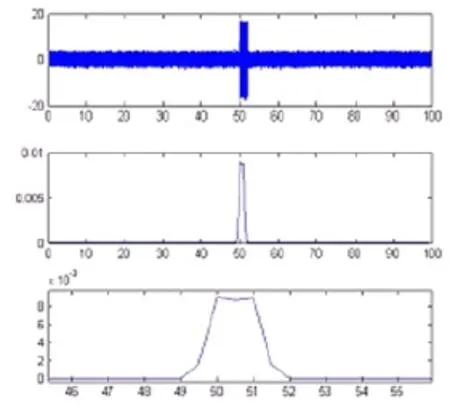
图2　信噪比为10dB的检测结果

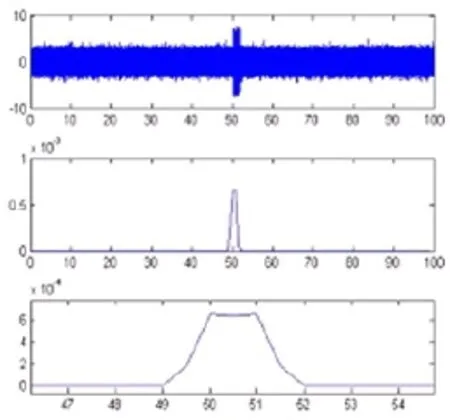
图3　信噪比为5dB的检测结果

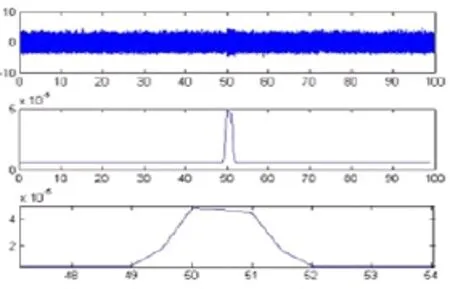
图4　信噪比为0dB的检测结果

图5　信噪比为-5dB的检测结果

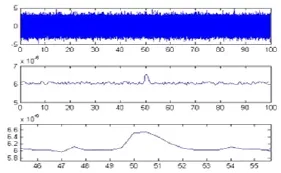
图6　信噪比为-8dB的检测结果

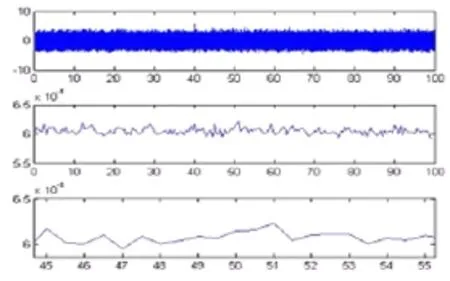
图7　信噪比为-10dB的检测结果

小结

通过上述仿真研究表明：基于似然函数比的瞬态信号判别方法可以较好地实现信噪比为-8dB以上的瞬态信号的判别，即能够确定瞬态信号的起始时刻和结束时刻，这也为后续的舰船瞬态信号的分析与评价奠定了基础。

10.3969/j.issn.1001-8972.2015.15.049