Coupling Multi-objective Constrained Optimization, Life Cycle Assessment, and Detailed Process Simulation for Potable Water Treatment Chains

Florin Capitanescu, Elorri Igos, Antonino Marvuglia, Enrico Benetto

Luxembourg Institute of Science and Technology （LIST）, Environmental Research and Innovation （ERIN） Department, 41-rue du Brill, L-4422 Belvaux, Luxembourg



Coupling Multi-objective Constrained Optimization, Life Cycle Assessment, and Detailed Process Simulation for Potable Water Treatment Chains

Florin Capitanescu†, Elorri Igos, Antonino Marvuglia, Enrico Benetto

Luxembourg Institute of Science and Technology （LIST）, Environmental Research and Innovation （ERIN） Department, 41-rue du Brill, L-4422 Belvaux, Luxembourg

Submission Info

Communicated by Beniamino Murgante

Potable water treatment chain

Life cycle assessment

Multi-objective optimization

Meta-heuristic global optimization algorithms

This paper deals with the optimization of key decision variables of a potable water production plant. To this end we propose a multi-objective constrained optimization approach which trades-off operational costs and environmental impact while satisfying outlet water drinkability criteria. The proposed solution approach consists in coupling a meta-heuristic global optimization algorithm and EVALEAU, which is a state-of-the-art process modelling - life cycle assessment （LCA） tool for simulating potable water treatment chains. The proposed eco-design optimization approach is successfully illustrated on a real-world model of a water production plant, and the relative performances of two highly praised stateof-the-art derivative-free global optimization algorithms, namely the Strength Pareto Evolutionary Algorithm （SPEA2） and Non-dominated Sorting Genetic Algorithm （NSGA-II）, are compared.

© 2015 L&H Scientific Publishing, LLC. All rights reserved.

1 Introduction

Life cycle assessment （LCA） is a standardized methodology, according to the ISO 14040 standard （2006）, which analyzes the lifecycle （i.e. generally from raw material acquisition through product disposal） environmental performance of any industrial process. LCA consists in fulfilling successively three tasks： goal and scope definition, life cycle inventory （LCI）, and life cycle impact assessment （LCIA）. LCI aims at computing the environmental burdens related to a product during its entire life cycle； it has been mathematically formalized in Heijungs and Suh （2002） and, in its matrix-based implementation, it consists in a two-step process which first solves a linear system of equations and then carries out a matrix multiplication. As LCI results often contain large amount of information which may be difficult to interpret, in order to facilitate decision making, LCIA aggregates LCI results into a few environmental impact categories, according to some suitable method such as ReCiPe in Goedkoop et al. （2008）, etc.

Because LCA per se does not provide levers for （optimally） acting on the various environmental impacts, in order to offer decision makers efficient solutions for improving the environmental impact of a process, LCA needs to be complemented by optimization tools, Azapagic and Clift （1999）. Furthermore the optimiza-tion of real-world processes has to be performed in most cases according to multiple and often conflicting specific criteria （e.g. economic, environmental, technical, etc.） while satisfying a set of technical operating constraints of the process.

The optimization of various industrial processes to further account for environmental constraints has been extensively investigated so far, as demonstrated in two recent survey papers： Jacquemin et al. （2012） and Pieragostini et al. （2012）. Most of the previous works assume that the process can be （approximately） modeled analytically by a set of equations enabling thereby resorting to suitable mature mathematical programming-based methods such as： linear programming in Azapagic and Clift （1998）, nonlinear programming in Gebreslassie et al. （2009）, mixed-integer linear programming in You et al （2012）, or mixed-integer nonlinear programming in Guillén-Gosálbez et al. （2008） and Grossman and Guillén-Gosálbez （2010）.

Comparatively with other research fields, the optimization of potable water treatment chains under LCA constraints has received very little attention up to now. The sole existing work in this field, Wallace et al.（2014）, performs a single-objective optimization of a water production plant by combining the Nelder-Mead local search algorithm and EVALEAU, which is a state-of-the-art process engineering - LCA tool described in Méry （2012） and Méry et al. （2013）. Although Wallace et al. （2014） initiates the LCA-based optimization of potable water production plants, it remains in a preliminary stage because： it does not consider multiple objectives or water quality constraints, and the local search algorithm utilized may be trapped into local optima.

This paper aims at correcting the above mentioned limitations by proposing a comprehensive multiobjective constrained optimization framework for the eco-design of a drinking water production plant and a solution approach which couples EVALEAU with appropriate state-of-the-art global search optimization algorithms such as Strength Pareto Evolutionary Algorithm （SPEA2）, described in Zitzler et al. （2002） or Nondominated Sorting Genetic Algorithm （NSGA-II）, proposed in Deb et al. （2000）. The advantage of these optimizers, over local search algorithms, is that they explore the design space globally and therefore have less chance to be trapped into local optima. In the absence of decision maker preference information, conflicting objectives （e.g. economic vs environment） will produce a set of optimal compromise solutions, called Pareto set. Also, the global optimizers are more suitable than classical derivative-based mathematical programming optimization methods for exploring complex Pareto fronts （e.g. irregular, discontinuous, etc.）.

It is important to emphasize that, as we will explain in detail in next Sections, the deep level of embedding of EVALEAU software makes impossible the expression of mathematical model of the problem in closed form and hence precludes taking an optimization approach based on classical derivative-based mathematical programming methods. Some among the main challenging features of the problem are： （i） some units process rely on an expert solver for simulating the equilibrium of chemical reactions （which may involve thousands chemical equations）； （ii） feedback loops are present in the process modelling； （iii） the LCIA results, operational cost, and outlet water quality depend on the simulation results of the whole chain. Therefore relying on derivative-free global optimizers for the optimization of a black-box problem as ours appears as a natural choice.

The remaining of the paper is organized as follows. Section 2 briefly describes the EVALEAU simulator. Section 3 provides the conceptual formulation of the optimization problem, explains the coupling approach and presents the global optimizers used （SPEA2 and NSGA-II）. Section 4 provides optimization results with these algorithms for a realistic model of a real-world potable water production plant. Section 5 concludes and provides directions for future work.

2 EVALEAU simulator for potable water treatment chain

EVALEAU is an integrated process modelling-LCA tool for prospective and retrospective simulation of potable water treatment chains, developed jointly by INSA Toulouse and the Public Research Centre Henri Tudor, to simulate and assess drinking water treatment chains, see Méry （2012） and Méry et al. （2013）. The salient features of the EVALEAU tool are the detailed modelling of potable water treatment unit operations andthe coupling with state of the art LCA tools.

The EVALEAU tool was developed in Umberto®1http：//www.umberto.de/en/and contains a library composed by a certain number of modules （see Fig. 1）, each module being a detailed and highly parameterized model of a specific water treatment process. The tool relies on the software Phreeqc®2http：//wwwbrr.cr.usgs.gov/projects/GWC_coupled/phreeqc/fs/FactSheetFS-031-02.htmlfor water chemistry calculation, detailed in Parkhurst and Appelo （2013） and its modules are linked to the Ecoinvent® LCI database, described in Weidema et al （2013）, for background processes （see Fig. 2）.

After extensive tests, Méry et al. （2013） reports that EVALEAU simulation results were validated within reasonable accuracy using measurements from an actual working plant. These results prove that the process modelling is sufficiently accurate, and, as a consequence, so is the LCA carried out in conjunction with the simulation. This provides incentives for a cost vs. environmental impact simulator-based optimization of key design variables of a drinking water production plant.

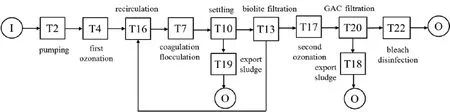
Fig.1. Simplified model of a real-world water treatment plant. I stands for “input”, O stands for “output”, and T stands for unit process.

3 The proposed optimization approach

3.1 Formulation of the multi-objective constrained optimization problem

The multi-objective optimization problem corresponding to a relevant operating scenario of a potable water production plant can be conceptually and compactly formulated as follows：

subject to：

where x is the vector of decision variables3For the sake of simplicity we make explicit only the decision variables of the optimization problem although there are also other“dependent” variables of the problem （e.g. water composition at the input and output of each process unit, etc.） whose values depend implicitly on the decision variables.（e.g., key design and operational parameters of the various water plant unit process）, the goal1f models the operational cost of the water production plant （e.g., costs of raw materials, chemicals, electricity, etc.）, the goal2f models the environmental impacts of the plant which can be calculated by an appropriate and widely agreed LCIA method such as the one we used here： ReCiPe method applied at midpoint level, see Goedkoop et al （2008）.

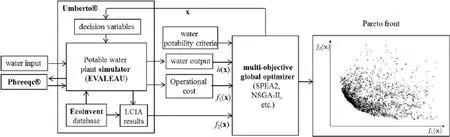
Fig.2. Software architecture of the proposed optimization approach coupling EVALEAU simulator with a multi-objective global optimizer.

Equality constraints （2） model the set of equations which describe the input-output mass flow for each unit process in the whole chain.

Inequality constraints （3） model the outlet water quality which is assessed according to the best class（which requires setting the limit hminto 80%） for potable water quality from the French evaluation grid SEQ Eau （2003）. The SEQ Eau grid defines five4The ranges （in %） of the five water quality classes are： ［0；20］, ［20；40］, ［40；60］, ［60；80］, and ［80；100］.classes of water quality, and satisfying its best water quality class also satisfies the French drinking water standards, described in the French water quality law （2001）. Upon recommendation from water production plant experts, we focus in this work on seven major aggregated parameters （e.g. total coliforms, total trihalomethanes, total organic carbon, Escherichia coli, faecal streptococci, turbidity, and conductivity） to enforce water drinkability, although the method can be easily incorporate other constraints. Inequality constraints （4） model physical limits of the decision variables.

3.2 Overview of the solution approach coupling an optimizer and the process simulation - LCA EVALEAU tool

Before presenting the proposed solution approach let us scrutinize the equality constraints （2） which model the water chain operation. The operation of any process unit i of the chain can be roughly described in an abstract way by the following input-output water flow set of equations （for the sake of simplicity one neglects other outputs than water, e.g. sludge, and different time-frames for chemical reactions）：

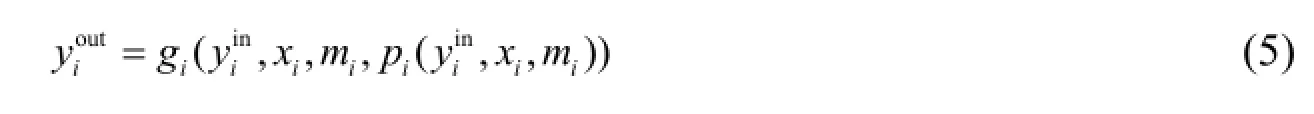
Due to the complexity of these equality constraints （e.g., non-convex, large scale, difficult to fully express in analytical form, feedback loops） and to the fact that the functions f1（x）,f2（x）, and h（x） further depend on the solution of these equality constraints, solving directly the optimization problem （1）-（4）, especially by means of classical mathematical programming methods, is impractical if feasible at all.

To overcome this difficulty we propose a solution approach, shown in Fig. 2, which couples the EVALEAU simulator with a multi-objective global optimizer （e.g., SPEA2, NSGA-II, etc.）. This approach breaks-down the optimization problem into two manageable blocks which are solved in a loop： （i） solution of equality constraints （2） obtained by running the EVALEAU simulator for a given value of decision variables x provided by the optimizer, and （ii） improvement of the solutions of the optimization problem （1）-（4） by theoptimizer, which is fed with the values of functions f1（x）,f2（x）, and h（x） evaluated by the EVALEAU simulator, and returns to the latter a promising value of decision variables x.

3.3 Global optimizers

SPEA2 and NSGA-II are mature second-generation （i.e. elitism-based） global meta-heuristic derivative-free multi-objective optimizers which have been successfully applied to many black-box optimization problems in various fields of research. Both are elitist multi-objective evolutionary algorithms aimed at finding or approximating the optimal set of trade-off solutions （i.e. the Pareto set and its image in the objectives space - the Pareto front）. Once an initial population is randomly generated an evolutionary algorithm, in its general form, repeats the following steps： evaluation （fitness assignment）, selection, crossover （or recombination） and mutation, until some termination criteria are met （e.g. a pre-defined maximum number of generations is reached, no progress in population quality is observed over the past few generations, etc.）.

Both algorithms are provided as free source code on the PISA platform, see Bleuler et al. （2003）. This platform facilitates user work by reliving the task of implementing the steps of the optimization algorithm which are independent of the problem （e.g. selection process） allowing the user to focus on the specific problem parts： generation, evaluation, recombination and mutation. Both algorithms have been adapted to the optimization problem of concern in this paper.

While a very detailed description of SPEA2 and NSGA-II algorithms can be found in Zitzler et al. （2002）and Deb et al. （2000）, respectively, a few distinctive features of both optimizers are highlighted hereafter.

3.3.1 SPEA2

The algorithm incorporates a fine-grained fitness assignment strategy （which takes into account for an individual the numbers of individuals it dominates and is dominated by, a nearest neighbor based density estimation technique, and an enhanced archive truncation method which guarantees the preservation of boundary solutions, as detailed in Zitzler et al. （2002）. SPEA2 operates with a population （archive） of fixed size, from which promising candidates are drawn as parents of the next generation. The resulting offspring then compete with the old ones for inclusion in the population.

3.3.2 NSGA-II

In order to improve population diversity, NSGA-II algorithm, described in Deb et al. （2000）, relies on the notion of crowding distance. The latter is calculated （in a parameter-free way） for each individual and represents a measure of how close an individual is to its neighbors. The crowding distance intervenes, together with the rank, in the process of parents' selection. Contrarily to SPEA2, NSGA-II does not use an external memory to store the best non-dominated individuals. To reduce the computational complexity the algorithm uses a fast non-dominated sorting approach. Also the elitist mechanism employed in the selection phase consists in combining the best parents and the best offspring obtained （with respect to fitness and spread）.

4. Numerical results and discussion

4.1 Description of the studied water plant and simulation tools

The optimization algorithm is applied to a realistic model of an existing French water treatment plant. The treatment chain of the inlet river water contains the major unit process （see Fig.1）： pumping, a first ozonation, coagulation/flocculation, settling, biolite filtration, a second ozonation, granular activated carbon （GAC） filtration, and bleach disinfection. The sludge produced during water treatment is discharged in the sewer system （the simulation of the sludge disposal has been excluded from the scope of the study）.

The simulations are run on a 2.70GHz/8GB computer. The EVALEAU tool runs in Umberto® 5.6 envi-ronment and is linked to the Ecoinvent® v2.2 LCI database for background processes. The environmental impact objective is computed using the scientifically sound Midpoint ReCiPe LCIA method, focusing only on climate change impact category （Global Warming Potential - GWP - factors based on 100 years-time horizon）.

4.2 Choice of effective decision variables for the optimization problem

The potable water production plant contains a set of 103 decision variables to be potentially optimized. However, given that, in the context of the optimization algorithms used, the simulation of the water treatment chain is computationally intensive （it takes in average around 120 seconds） a limited number of effective decision variables for the problem of concern should be carefully chosen. In a first step, expert drinking water plant engineering judgment allowed to reduce the full decision variables set to a subset of 18 potentially more sensitive variables, evenly selected from almost all process units. In order to further filtering out less sensitive or counterproductive variables for the optimization problem of interest, we have applied, for one parameter at the time, a brute-force sensitivity calculation. The latter consists in moving, whenever possible, each variable from its current position to its lower or upper bound, and running EVALEAU simulation in order to gather the impact of variable variation on both the two objectives and the inequality constraints.

Table 1 provides the results obtained with this technique for five typical variables. In this table the initial value of each variable is shown in bold and only the inequality constraint which are mostly influenced by the variable change is shown （actually, apart from the variable coagulant dose, one can remark that the other variables have negligible impact on the inequality constraints）. One can observe that acting on the variable pure oxygen percentage in the feed gas leads to a conflict between the two objectives （i.e. a significant reduction of cost at the expense of a large increase in the environmental impact）, while increasing the value of the GAC regeneration frequency variable is beneficial for both objectives. Note that the variable coagulant velocity gradient is already set at an optimal value, as any increase in its value deteriorates both objectives； hence it makes no sense to include it into optimization. The same treatment is applied to variable T10/T contact time ratio which has an insignificant impact on both objectives.

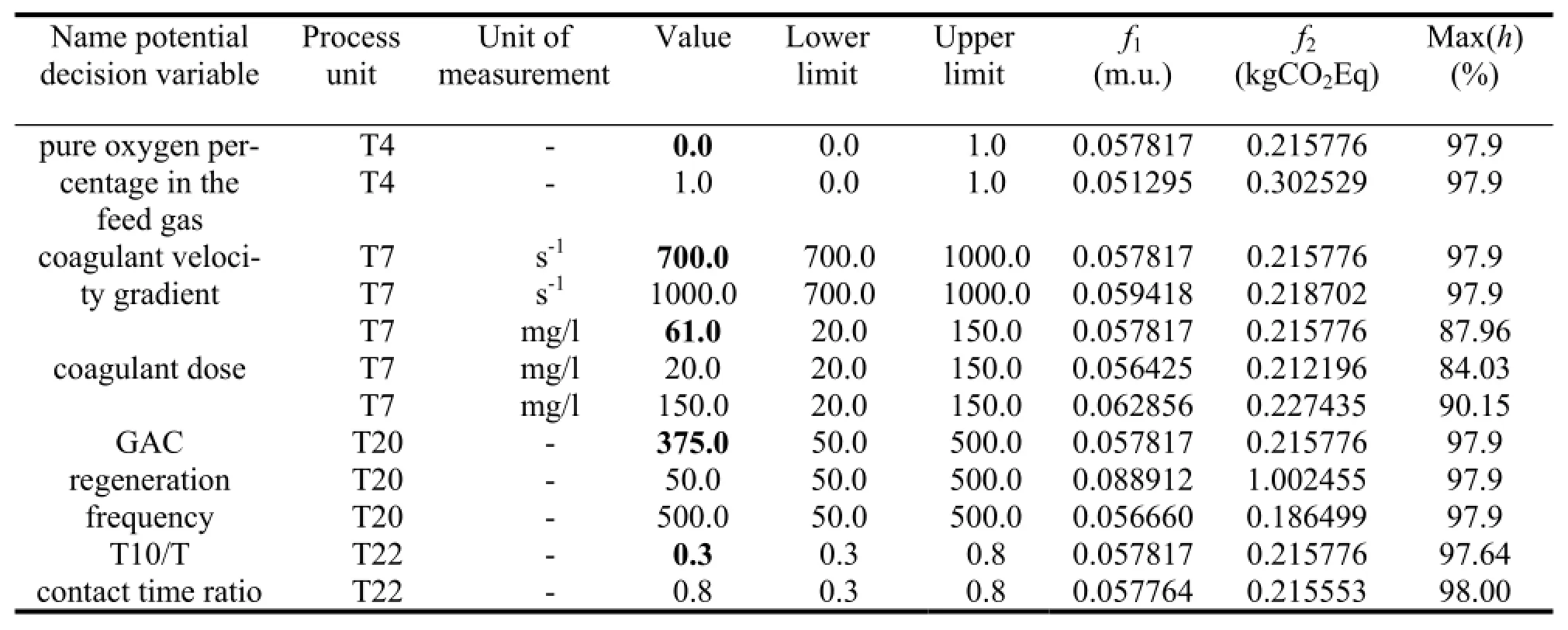
Table 1 Brute-force sensitivity analysis measuring the impact of variable change on the objectives f1, expressed in monetary units （m.u.） per 1m3of water treated, f2,expressed in kgCO2Eq per 1m3of water treated, and constraints h

This technique allows selecting finally only six decision variables as the most effective ones for the problem of concern （see Table 2）： the ozone transfer efficiency and the pure oxygen fraction in feed gas in both T4 and T17 ozonation unit processes （see Fig. 1）, the coagulant dose in the coagulation/flocculation unit （T7）, and the GAC regeneration frequency in the GAC filtration unit （T20）.

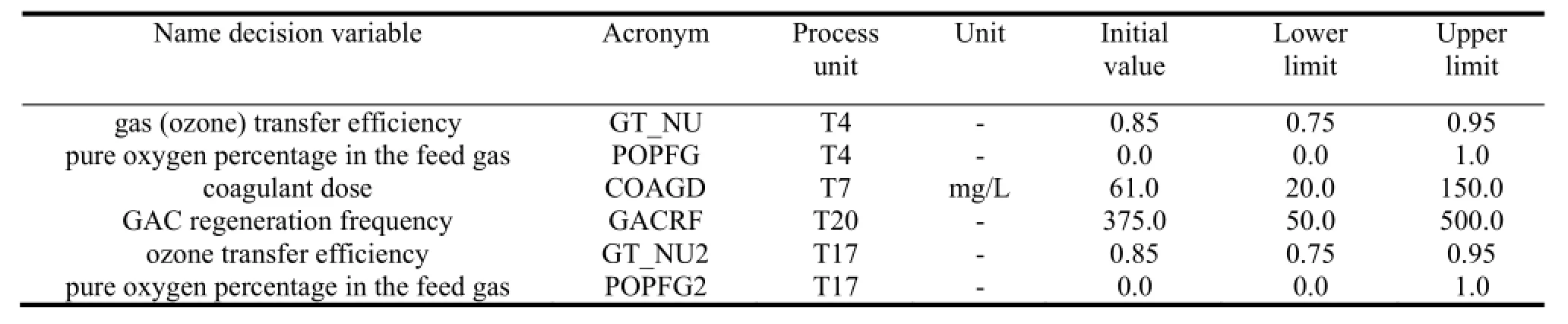
Table 2 Decision variables data

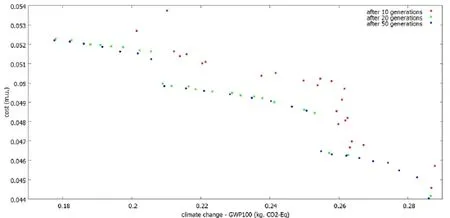
Fig.3. SPEA2： Best population evolution over generations and Pareto front （blue color）.

4.3 Results using SPEA2 global optimizer

SPEA2 algorithm is run using a population size of 24 individuals （or solutions） during 50 generations （since no significant improvement in the Pareto front has been observed by using larger number of generations） and using full replacement of the population. The variation operators are the SBX （simulated binary crossover）and the polynomial mutation operator.

Fig. 3 shows with blue color the Pareto front which contains cost vs. climate change trade-off optimal solutions. The front is composed of three disjoint concave parts. Since the initial water plant operating point（not shown in the figure for the sake of legibility） corresponds to a cost of 0.0578 monetary units （m.u.） per 1m3of water treated and a GWP100 environmental impact of 0.2158 kg CO2-Eq one can observe that the optimal solutions of the first concave part of the Pareto front （left side in the figure） improves both objectives. In particular the solution with the lowest environmental impact leads to a decrease of operational cost and GWP100 characterization factor of 9.7% and 18.0%, respectively.

The figure also shows the best population evolution during generations. Note that if after 10 generations the best population is still far from the Pareto front and contains dominated solutions, after 20 generations it approaches very closely the Pareto front and all solutions of the front are non-dominated. However, after 20 generations the best population distribution and diversity is insufficient （e.g. a small number of points in the right part of the figure）. Given that the shape of the Pareto front is not very complex, the convergence is hence reached after a relatively small number of generations. However, the computational effort of the algorithm, which corresponds mainly to 24x50=1200 runs of EVALEAU to evaluate the objectives and the constraints, amounts to 37.67 hours and is proportional and mostly due to EVALEAU running time （around 113 seconds）. This computational burden fully justifies the approach taken in this paper to identify the smallest possible subset of effective decision variables instead of working with the entire set. Although this computational effort is not a big concern at the planning stage timeframe of our optimization problem, further improvement in both algorithm and EVALEAU tool are desirable.

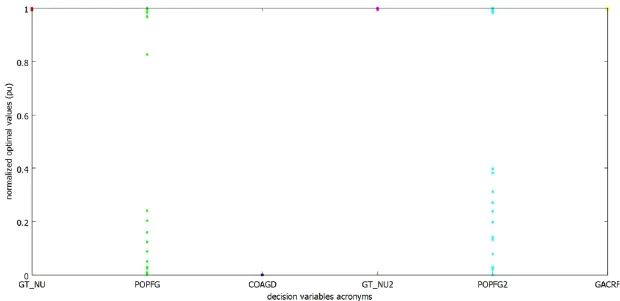
Fig.4. Pareto-optimal settings of decision variables in per unit （p.u.） normalized to interval ［0；1］.

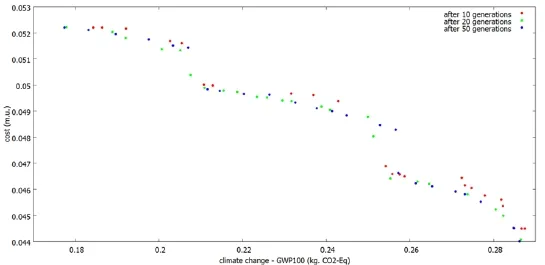
Fig.5. NSGA-II： Best population evolution over generations.

Figure 4 provides the Pareto-optimal set （i.e. the values of decision variables corresponding to the Pareto front shown in Fig. 3）. Note that four variables namely GT_NU, COAGD, GT_NU2, and GACRF take for all solution the same value （as expected they hit either the upper or the lower physical bound） which means that both objectives are improved for higher values of GT_NU, GT_NU2 and GACRF, and lower value of COAGD. On the other hand the optimal values of the two other variables （POPFG and POPFG2） present a certain spread in their range （still the spread is not too large aiding decision makers） and thereby can improve one objective to the detriment of the other.

4.5 Results using NSGA-II global optimizer

NSGA-II algorithm is run with recommended settings for a population size of 24 individuals （12 children being generated from 12 parents） during 50 generations5Note that NSGA-II evaluates at each generation 12 new individuals, except the first generation, where the 24-individuals initial population in generated. To ensure a fair comparison with SPEA2, which creates 24 new individuals at each generation, we consider that a generation requires the same number of evaluations, i.e. 24 for both algorithms..

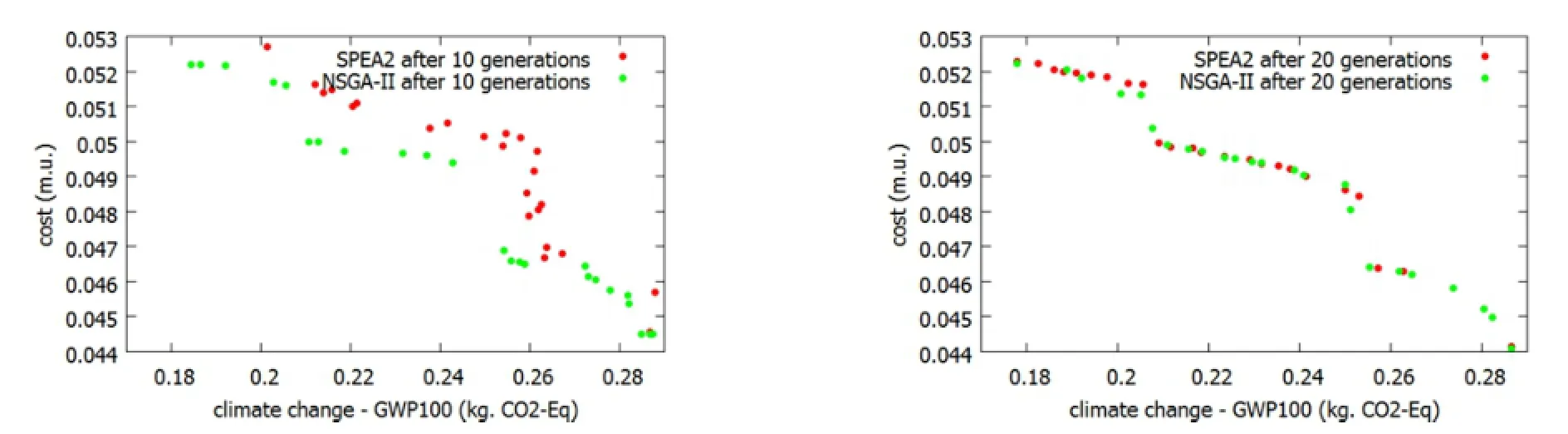
Fig.6. SPEA2 vs NSGA-II： best population evolution after 10 generations （left plot） and 20 generations （right plot）.

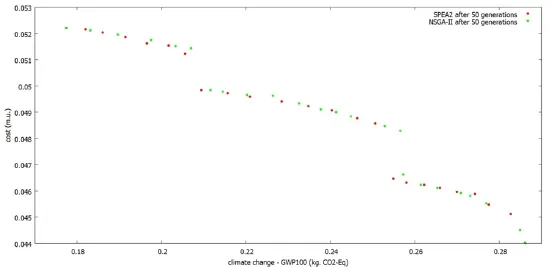
Fig.7. SPEA2 vs NSGA-II： best population evolution after 50 generations.

Fig. 5 shows a salient feature of this algorithm, i.e. it is able to approach in a small number of generations the Pareto front, as the differences between the three fronts is not significant. In particular the front shape after only 10 generations is already very good. On the other hand, since the algorithm tries to make a compromise between both the quality of solutions and solutions distribution, one can note that between generation 20 and 50 a few good quality non-dominated solutions are lost, phenomenon explained in Zitzler et al. （2004）.

4.6 SPEA2 vs NSGA-II

Figures 6 and 7 display the front obtained with both algorithms, SPEA2 and NSGA-II, after a certain number of generations. From the left plot of Fig. 6 one can first observe that after 10 generations NSGA-II front is much better （in terms of non-dominance, distribution and spread of solutions） than the one of SPEA2. This is to be expected given the NSGA-II algorithmic feature which focuses on combining best parents and best children. However, after 20 generations, the advantage of NSGA-II diminishes considerably, as shown in the right hand side plot of Fig. 6. As generations evolve, see Fig. 7, SPEA2 slightly outperforms NSGA-II, since the latter discards some good quality solutions in order to improve front diversity.

Due to the very large computational effort of this optimization problem, conducting a comprehensive comparison among these algorithms is very challenging. Nevertheless this preliminary comparison underlines some of their features： in a first phase of optimization NSGA-II approaches the Pareto front at a faster pace than SPEA2, while the latter keeps a better diversity of solutions which prevents convergence oscillations （as good quality solutions can be dismissed to improve the front diversity）.

5. Conclusions and future works

This paper has proposed a multi-objective constrained optimization approach for the eco-design of potable water treatment chains. The paper has demonstrated, using a real-world model of water production plant, the feasibility of the proposed approach, which couples a global optimization algorithm and EVALEAU, which is a state-of-the-art process modelling - life cycle assessment tool for simulating potable water treatment chains. The proposed optimization methodology is generic and can be applied to other drinking water production plants provided that an additional effort of unit process modelling is performed.

Although the paper focuses on the trade-off between operational cost and climate change （computed via ReCiPe midpoint method）, other environmental impact metrics （e.g. other midpoint impact categories, ReCi-Pe single score, etc.） could be incorporated preferably as constraints （since the computational effort grows dramatically as the number of objectives increases）.

The paper also proposed a sensitivity-based technique to quickly identify the most efficient decision variables for the optimization problem aiding thereby the decision maker and reducing the computational burden. We highlighted the presence of two classes of decision variables： non-conflicting （e.g. GT_NU, COAGD, GT_NU2, and GACRF）, which are able to improve both objectives, and antagonist （e.g. POPFG and POPFG2） which can improve one objective to the detriment of the other. Optimization results suggest that operating conditions with a better trade-off between costs and environmental impacts with respect to the current operating point of the water plant can be obtained by setting GT_NU, GT_NU2, and GACRF to their upper bounds, setting COAGD to its lower bound； while setting POPFG and POPFG2 within their bounds generates various trade-off optimal solutions. In terms of improvements compared to the current operating point of the water plant, the solution with the lowest environmental impact leads to a good decrease of both operational cost and climate change of 9.7% and 18.0%, respectively.

The two state-of-the-art global optimization algorithms investigated, SPEA2 and NSGA-II, showed comparable performances in terms of quality of the optimal solutions and convergence speed.

The results showed that, since the core simulator is time consuming, the optimization approach is expected to be very computationally expensive. Although this computational effort is not a big concern at the planning stage timeframe of our optimization problem, further improvement in both the optimization algorithm and EVALEAU tool are desirable. Future work will therefore explore the potential reduction of the computational burden of the algorithm along techniques proposed in Jones et al. （1998） for expensive black-box optimization problems, or by using hybrid algorithms combining global and local search methods, Sindhya et al.（2013）. Future work is also planned to extend the optimization approach so as to be able to manage the variability of operating conditions.

Acknowledgements

The authors acknowledge the funding from National Research Fund （FNR） Luxembourg in the framework of the OASIS project （CR13/SR/5871061）. The authors also wish to thank Dr. Aras Ahmadi （INSA Toulouse, France） for data provided and support in setting-up the multi-objective constrained optimization problem, and Dr. Richard J. Wallace （Insight Centre for Data Analytics, Cork, Ireland） for having initiated the research in this topic during a research visit at the Public Research Centre Henri Tudor （which has now become part of the LIST）, and for providing his code which lighten our programming effort regarding the use of Umberto® functionalities.

Azapagic, A. and Clift, R. （1998）, Linear Programming as a Tool in Life Cycle Assessment, The International Journal of Life Cycle Assessment， 3, 305-316.

Azapagic, A. and Clift, R. （1999）, Life Cycle Assessment and Multiobjective Optimisation, J. Clean. Prod., 7, 135-143.

Bleuler, S., Laumanns, M., Thiele, L. and Zitzler, E. （2003）, PISA - A Platform and Programming Language Independent Interface for Search Algorithms, In： Fonseca C.K.， Fleming P.J.， Zitzler E.， Deb K. and Thiele L. （Eds.）， Evolutionary Multi-Criterion Opti-mization （EMO 2003）， LNCS， Berlin, Springer, 494-508.

Deb, K., Agrawal, S., Pratap, A. and Meyarivan, T. （2000）, A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multiobjective Optimization： NSGA-II, PPSN VI （Eds. Schoenauer M. et al.）， LNCS, 1917, 849-858.

French water quality law, Décret n° 2001-1220 du 20/12/01 relatif aux eaux destinées à la consommation humaine （in French）, http：//www.ineris.fr/aida/consultation_document/2955.

Gebreslassie, B.H., Guillén-Gosálbez, G., Jiménez, L. and Boer, D. （2009）, Design of environmentally conscious absorption cooling systems via multi-objective optimization and life cycle assessment, Applied Energy, 86 （9）, 1712-1722.

Goedkoop M.J., Heijungs R, Huijbregts M., De Schryver A., Struijs J., Van Zelm R. （2008）, ReCiPe 2008, A life cycle impact assessment method which comprises harmonised category indicators at the midpoint and the endpoint level, First edition Report I：Characterisation, 6 January 2009, http：//www.lcia-recipe.net

Grossman, I.E. and Guillén-Gosálbez, G. （2010）, Scope for the Application of Mathematical Programming Techniques in the Synthesis and Planning of Sustainable Processes, Computers & Chemical Engineering, 34, 1365-1376.

Guillén-Gosálbez, G., Caballero, J.A. and Jiménez, L, （2008）, Application of Life Cycle Assessment to the Structural Optimization of Process Flowsheets, Industrial & Engineering Chemistry Research, 47, 777-789.

Heijungs, R. and Suh, S. （2002）, The Computational Structure of Life Cycle Assessment, Kluwer Academic, Dordrecht.

ISO 14040： Environmental Management - Life Cycle Assessment - Principles and Framework, （2006）, International Organisation for Standardisation, Geneva （Switzerland）.

Jacquemin, L., Pontalier, P.Y., and Sablayrolles, C. （2012）, Life Cycle Assessment （LCA） Applied to the Process Industry： A Review. The International Journal of Life Cycle Assessment, 17, 1028-1041.

Jones D., Schonlau M., and Welch W. （1998）, Efficient global optimisation of expensive black-box functions, Journal of Global Optimisation, 13, 455-492.

Méry Y. （2012）, Development of an Integrated Tool for Process Modelling and Life Cycle Assessment - Ecodesign of Process Plants and Application to Drinking Water Treatment, PhD Thesis, LISBP INSA Toulouse, France.

Méry, Y., Tiruta-Barna, L., Benetto, E., and Baudin, I. （2013）, An Integrated “Process Modelling-Life Cycle Assessment” Tool for the Assessment and Design of Water Treatment Processes, The International Journal of Life Cycle Assessment, 18, 1062-1070.

Parkhurst, D.L. and Appelo, C.A.J. （2013）, Description of input and examples for PHREEQC version 3--A computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations： U.S. Geological Survey Techniques and Methods, book 6, chap. A43, 497 p.

Pieragostini, C., Mussati, M.C. and Aguirre, P. （2012）, On Process Optimization Considering LCA Methodology, Journal of Environmental Management, 96, 43-54.

SEQ-Eau （version 2） Water Quality Evaluation System in France, （2003）, http：//sierm.eaurmc.fr/eaux-superficielles/fichierstelechargeables/grilles-seq-eau-v2.pdf, （in French）.

Sindhya K., Miettinen K., Deb K. （2013）, A hybrid framework for evolutionary multi-objective optimization, IEEE Transactions on Evolutionary Computation, 17, 495-511.

Wallace, R.J., Marvuglia, A., Benetto. E., and Tiruta-Barna, L. （2014）, A New Approach to Optimization with Life Cycle Assessment：Combining Optimization with Detailed Process Simulation, ICCSA 2014 （Eds. Murgante B. et al.）， LNCS, 8581, 707-720.

Weidema, B. P., Bauer, C., Hischier, R., Mutel, C., Nemecek, T., Reinhard, J. and Wernet, G. （2013）, Overview and methodology：Data quality guideline for the ecoinvent database version 3， Swiss Centre for Life Cycle Inventories.

You, F., Tao, L., Graziano D.J., and Snyder S.W. （2012）, Optimal design of sustainable cellulosic biofuel supply chains： Multiobjective optimization coupled with life cycle assessment and input-output analysis, AIChE Journal, 58 （4）, 1157-1180.

Zitzler, E., Laumanns, M., and Bleuler, S. （2004）, A tutorial on evolutionary multiobjective optimization, in Gandibleux, X. et al.（Eds.）, Metaheuristics for Multiobjective Optimisation, Springer, Heidelberg, 3-37.

Zitzler, E., Laumanns, M., and Thiele, L. （2002）, SPEA2： Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization, In： Evolutionary Methods for Design, Optimisation and Control with Application to Industrial Problems （Eds. Giannakoglou K.C. et al.）, Proceedings of the EUROGEN2001 Conference, Athens, Greece, 95-100.

30 November 2014

.

Email address： florin.capitanescu@list.lu

ISSN 2325-6192, eISSN 2325-6206/$- see front materials © 2012 L&H Scientific Publishing, LLC. All rights reserved.

10.5890/JEAM.2015.03.001

Accepted 30 July 2015

Available online 1 September 2015