基于MATLAB的储药柜优化设计

王建芳，陈斯养

（1.西安铁路职业技术学院陕西西安710016；2.陕西师范大学数学与信息科学学院，陕西西安710062）

基于MATLAB的储药柜优化设计

王建芳1，陈斯养2

（1.西安铁路职业技术学院陕西西安710016；2.陕西师范大学数学与信息科学学院，陕西西安710062）

针对储药柜优化设计问题，提出逐步分裂的迭代算法。该方法是在类型最少方案的基础上，为获得大幅冗余降低率，对隔板间距类型进行逐步拆分，以减少冗余。首先，通过Excel对数据进行统计分析，其次，利用Matlab给出分类冗余曲线拟合图，确立合理的横版和竖版间距类型，最后，根据药品日需量计算出最少需要的储药柜个数。结果证明了该方法确立储药柜规格的合理性。

储药柜；隔板类型；冗余；多项式拟合

目前，国内各级医院正迅速向现代化管理迈进，自动发药系统对药房有效管理药品，降低管理成本起到了很大的推动作用。文献［1］对其设计进行了研究。本文在此基础上，根据2014“高教社杯”全国大学生数模竞赛D题提供的数据和要求，通过建立优化模型，对储药柜的设计进行了具体研究。本研究可为医院计划性购置储药柜数量及药品摆放提供可靠的参考依据。

1　问题的提出

储药柜通常由若干个储药槽组成。为保证药品准确发放并从储药槽内顺利出入，一个储药槽只能摆放同一种药品，药盒与竖板、横板之间应留2 mm间隙，药盒在推送过程中不能出现并排重叠、侧翻或水平旋转。根据要求讨论以下问题：

1）设计合理的竖板间距类型。要求竖板间距类型尽可能少，总宽度冗余尽可能减少。

2）在问题1）基础上，确定横板间距类型。使得储药柜总平面冗余尽可能小，且横板间距类型也尽可能少。

3）计算每种药品需要储药槽个数，并计算最少需要储药柜个数。

2　竖板类型确定

首先，定义重叠、侧翻和水平旋转3种现象。假设竖板间距类型最少为k类，药槽宽度为Yk，药盒长度为xi，宽度为yi，高度为hi。

重叠：当药槽宽度小于两倍的药盒宽度时，药盒在储药槽内推送过程中不会出现并排重叠的现象，即Yk＜2yi。

侧翻：当药槽的宽度小于药盒宽度和药盒高度的对角线时，药盒在储药槽内推送过程中不会出现侧翻的现象，即Yk＜

水平旋转：当药槽的宽度小于药盒长度和药盒宽度的对角线时，药盒在储药槽内推送过程中不会出现水平旋转的现象，即

其次，药盒与两侧竖板之间应留2 mm间隙，即Yk≥yi+2。

问题1要求竖板间距类型尽可能少，总宽度冗余尽可能减少。假设竖板间距类型为k类，总宽度冗余为rs，则可得到如下模型［2］：

假设每个Yk可放mk种药品，且，若让每个Yk重复mk次，则每类药对应槽宽构成矩阵Ai，从而得到总宽度冗余为

如果将竖版按宽度归为47类，每类药宽对应频数为fi，每个Yk对应药宽为nk种，且若让每个Yk重复nk次，则每类药宽对应槽宽构成矩阵Bi，从而得到总宽度冗余为

对附件1数据用excel命令countif（D：D，H2）统计可得到竖版47类及每类对应的频数，并做条形图如图1。由图可知药盒宽度在18～25 mm范围内的药盒数量普遍较多，如果在其范围内适当增加竖板间距类型，并以频率较高的药盒宽度作为该种竖板间距类型中所能放下的最大药盒，则可以有效的降低总宽度冗余。根据图像的峰值和平坦度，将竖板间距类型分为5～12类，并通过（3）式算出每种分类对应的总宽度冗余（见表1）。然后通过Matlab拟合，得到k与rs之间的函数关系，最后确定出总宽度冗余rs尽可能小时对应竖板间距类型k的最小值。

1）取k=5，6，7…12，算出对应总宽度冗余rs

2）对k与rs拟合，确定函数关系

将表1中的k作为自变量，总宽度冗余rs作为因变量，运用Matlab软件［3］拟合（见图3），得出竖板类型k与宽度冗余rs之间的函数关系为

表1　竖版分类冗余数值表Tab.1Vertical version classification redundant data table

图1　药盒宽度-频数图Fig.1Box width-frequency diagram

3）确定rs尽可能小时对应k的最小值

表2　竖版分类取值表（k=12）Tab.2Vertical version classification value table（k=12）

3　横板类型确定

问题2要求横板间距类型尽可能少的情况下，尽可能减少总平面冗余，而平面冗余=高度冗余*宽度冗余，在问题1的基础上，竖版类型不变，宽度冗余则为一定值，那么，求解平面冗余尽可能小的问题就可转化为求高度冗余尽可能小的问题。

假设横板间距类型为k类，总高度冗余为rh，槽高为Hk，药盒高为Hi，则可得到如下模型［4-5］

假设每个Hk可放αk种药品，且若让每个Hk重复αk次，则每类药对应槽高构成矩阵Ci，从而得到总高度冗余为

如果将横版按高度归为98类，每类药高对应频数为gi，假设槽高为Hk，每个Hk对应药高为bk种，且若让每个Hk重复bk次，则每类药高对应槽高构成矩阵Di，从而得到总高度冗余为

对附件1数据用excel命令countif（C：C，H2）统计可得到横版98类及每类对应的频数，并做条形图如图2。由图可知药盒高度在60～82 mm范围内的药盒数量普遍较多，如果在其范围内适当增加横板间距类型，并以频率较高的药盒高度作为该种横板间距类型中所能放下的最大药盒，则可以有效的降低总高度冗余。根据图像的峰值和平坦度，将横板间距类型分为8～25类，并通过（7）式算出每种分类对应的总高度冗余（见表3）。然后通过matlab拟合，得到k与rh之间的函数关系，最后确定出总高度冗余rh尽可能小时对应的竖板间距类型k的最小值。

1）取k=8，10，12，14，16，18，20，25，算出对应总高度冗余rh

2）对k与rh拟合，确定二者函数关系

将表3中的k作为自变量，总宽度冗余rh作为因变量，运用Matlab软件拟合（见图4），得出横板类型k与高度冗余rh之间的函数关系为

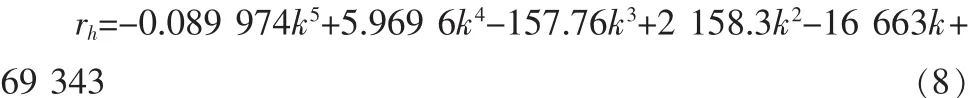
表3　横版分类冗余数值表Tab.3Horizontal version classification redundant numerical table

图2　药盒高度-频数图Fig.2Box height-frequency diagram

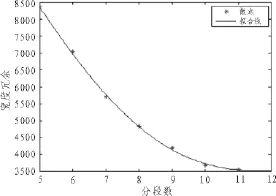
图3　宽度冗余图Fig.3Width redundant diagram

图4　高度冗余图Fig.4Height redundant diagram

3）确定rh尽可能小时对应k的最小值

对（8）式求二阶导数，并令rh″=0，得到k=18，即总高度冗余rh尽可能小时，横板类型k=18，此时对应总高度冗余rh=5 207。竖板类型k=18时，每种类型对应的药盒规格及数量见表4。

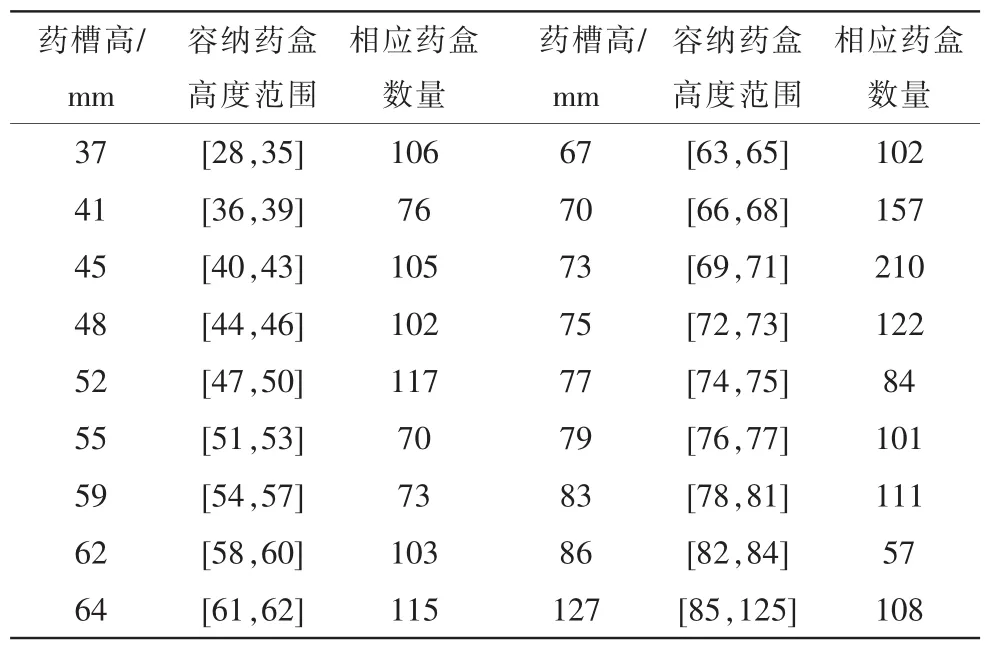
表4　横版分类取值表（k=18）Tab.4Horizontal version classification value table（k=18）

4）储药柜初步设计方案

由以上计算得出，储药柜横版类型为18类，竖版类型为12类，则药槽的类型一共有18×12=216种。

5）平面冗余的符合性检验

储药柜规格：宽度不超过2.5 m、高度不超过1.5 m。通过Matlab对平面冗余进行符合性检验［6］，计算得到面积误差很小，为0.126 2 m2，在允许范围内，故符合要求。

4　储药槽和储药柜需求量确定

4.1计算每种药品需要储药槽个数

根据附件2数据，在储药槽长度为1.5 m且每天仅集中补药一次的情况下，设Pi为第i种药品需要的储药槽个数；xi为第i种药盒长度；Qi为第i种药品每日最大需求量。则有：

4.2计算最少需要储药柜个数

设hi为第i类横版高度，sj为第j类竖版宽度，xij为第i类横版第j类竖版所需药槽数，则需要的储药柜为

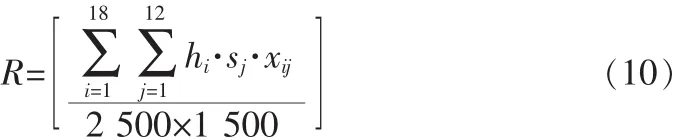
用Matlab编程计算得出需要1.307 6个储药柜，因此，在满足药房储药需求的情况下，至少需要2个储药柜。本问题的求解忽略了横向和竖向隔板的厚度影响，对于实际应用会导致一些问题，还需要在实践中进一步改善。

5　结束语

该模型推理严谨，可操作性强。具有推广使用价值。在数据统计时运用Matlab程序和Excel统计筛选功能，提高了处参考文献：

理数据的效率；在模型建立与求解中，采用多项式拟合法，找出了变量之间的相互关系，可靠性强.可进一步推广到大型图书馆书柜的设计，超市货物的摆放及集装箱装箱等问题处理中，具有一定的实用价值。

［1］张斐.药房全自动发药系统［J］.物流技术（装备版），2013（5）：1-3.

［2］孙晓娟，刘晓可.储药柜的设计数学模型的分析与求解［J］.才智，2014，11（32）：1-3.

［3］胡良剑，孙晓君.MATLAB数学实验［M］.北京：高等教育出版社，2006.

［4］姜启源，谢金星，叶俊.数学模型［M］.北京：高等教育出版社，2003.

［5］肖华勇.实用数学建模与软件应用［M］.西安：西北工业大学出版社，2008.

［6］韩中庚.数学建模实用教程［M］.北京：高等教育出版社，2012.

Medicine storing cabinet optimization design based on MATLAB

WANG Jian-fang1，CHEN Si-yang2
（1.Xi'an Railway Vocational Technical College，Xi'an 710016，China；2.College of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710062，China）

A gradually splitting iterative algorithm is suggested in this article to optimizing the medicine storing cabinet design. This method，basing on the least type solution，analyses the baffle spacing type to achieve a substantial redundancy reduction rate，thus to reduce the redundancy，This is done by firstly statistically analyzing the data via Excel，and secondly providing a classified redundant curve fitting chart via matlab to establish a reasonable horizontal and vertical version of spacing type，as well as by calculating the least number of storing cabinets needed，which turns out to prove the rationality of applying this method to establish storing cabinets'specifications.

medicine storing cabinet；baffle type；redundancy；polynomial fitting

TN102

A

1674－6236（2015）22-0004-03

2015-01-12稿件编号：201501088

国家自然科学基金资助项目（10871122，11171199）

王建芳（1972—），女，陕西西安人，硕士，副教授。研究方向：教学改革与数学建模。