三维强变异渗透系数随机场生成
王开丽,孙 磊,王立勇,孟 夏
(1.水利部松辽水利委员会,吉林长春130021;2.青岛市水利勘测设计研究院有限公司,山东青岛266071)
三维强变异渗透系数随机场生成
王开丽1,孙磊1,王立勇1,孟 夏2
(1.水利部松辽水利委员会,吉林长春130021;2.青岛市水利勘测设计研究院有限公司,山东青岛266071)
渗透系数的空间变异性是影响地下水运动的主要因素。研究利用改进的连续随机增加方法生成了渗透系数的对数(lnK)符合分维布朗运动(fBm)和分维Levy运动(fLm)的随机场,并对其统计特征进行了分析验证。结果表明:符合fBm和fLm统计特征的lnK随机场表现出强烈的空间变异性,其中fLm条件的lnK随机场的空间变异性更强,能更好反映地质介质中渗透系数呈现急剧变化的强变异性;符合fLm统计特征的lnK增量的概率密度分布(间距为1)符合Levy稳定分布且具有仿射不变性。
渗透系数;空间变异性;分维布朗运动;分维Levy运动
1 理论基础
1.1分维布朗理论与分维Levy理论
fBm是将空间随机变量(如lnK)在空间上的随机变化看作是具有分维特征的布朗随机游动,而将其增量处理成符合fGn的随机变量。设一维随机函数B(x)为分维布朗函数,即mB(x)=fBm,它的空间随机变化的统计特征由其增量函数nB(x,h)确定,定义为nB(x,h)=m(x+h)-m(x)=fGn,满足高斯分布,其概率密度函数GPDF(x)为:
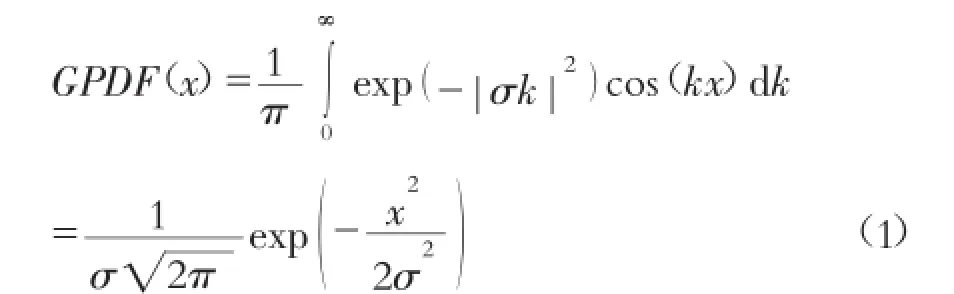
式中:σ为正态分布的标准差。
同理fLm是将空间随机变量(如lnK)在空间上的随机变化看作是具有分维特征的Levy随机游动,而将其增量处理成符合fLn的随机变量。即mL(x)=fLm,nL(x,h)=fLn。其中fLn的概率分布为Levy稳定分布,其概率密度函数LPDF(x)为:
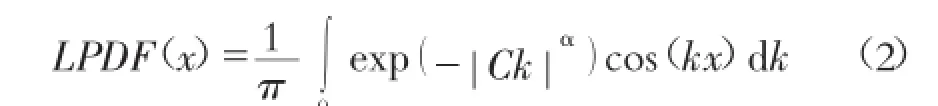
式中:C和a为表征Levy稳定分布特征的参数,C为宽度参数(Cα类似于正态分布的方差),α(0<α≤2)为决定LPDF(x)分布整体特征的指数,它使得Levy稳定分布的尾部按照P(|x|≥u)→uα衰减。与式(1)相比,式(2)的主要特征是它的尾部衰减比式(1)缓慢而且具有无限的二阶矩及以上高阶矩。同时α表征LPDF(x)空间分布偏离正态分布的程度,α越小,其偏离程度越明显,LPDF(x)尾部衰减越缓慢,即拖尾现象越明显。此分布特征使得LPDF易于描述局部尺度区域内在小尺度上呈急剧变化的地质介质的空间变异性(如沉积含水层的层状介质的垂直剖面上水力参数的急剧变异)。
fBm与fLm作为典型的分维随机模型,二者均具有仿射变换后的统计特征不变性(仿射不变性),即对随机函数nB(x,h)和nL(x,h)进行尺度变化后得到的随机函数nB(x,h)和nL(x,rh)满足:
1)nB(x,rh)=mB(x+rh)-mB((x)仍然具有高斯分布;同理nL(x,rh)=mL(x+rh)-mL(x)仍然具有Levy稳定分布;

2)nB(x,rh)与nB(x,h)所对应的高斯分布的标准差σrh与σh之间满足:式中:σrh与σh分别对应增量间距为rh和h时高斯分布的标准差;r为增量间距的放大倍数;H为Hurst系数(0<H<1)。
同理,nL(x,rh)与nL(x,h)所对应的Levy稳定分布的宽度参数与之间满足:
Crh=rHCh(4)式中:Crh与Ch分别对应增量间距为rh和 h时Levy稳定分布的宽度参数。式(3)与式(4)统称为分维模型的仿射不变性。当α=2时,Levy稳定分布即转化为高斯分布,式(4)与式(2)分别转化为式(3)与式(1),此时高斯分布的方差与Levy稳定分布条件下的宽度参数之间满足:
σ2=2C2(5)
因此可以说,fLm是fBm的推广,fBm是fLm的特殊情形。
Lu等(2003)开发了三维的SRA算法程序SRA3DC来生成符合fBm与fLm统计特征的随机空间变量。
1.2渗透系数随机场的验证
生成的lnK随机场是否具有fBm的统计特征,需验证:
1)lnK增量是否具有高斯分布;
2)不同间距的lnK增量的方差是否满足仿射不变性(式(3))。
其中,不同间距的lnK增量的方差通过离散分析进行估算,在此不作赘述,详情可参考Lu等论述。同理生成的lnK随机场是否具有fLm的统计特征,需验证:
1)lnK增量是否具有Levy稳定分布;
2)不同间距的lnK增量的宽度参数是否满足仿射不变性(见式(4))。
其中,不同间距的lnK增量的宽度参数及分位数分析可按如下公式进行估算:
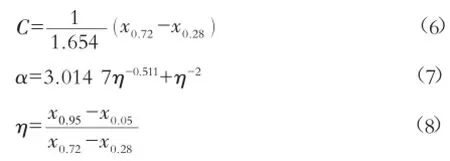
式中:x0.72,x0.28,x0.95与x0.05分别对应lnK增量的概率分布的0.72,0.28,0.95与0.05分位数。
2 符合fBm与fLm的lnK随机场生成及其验证
利用SRA3DC生成符合fBm与fLm统计特征的lnK随机场的一次实现结果表明:fBm与fLm条件下,lnK均表现出强烈的空间变异性。其中fBm条件下lnK的取值范围为(0~4),相对较集中;fLm条件下显示lnK的取值范围为(-4~12)。这说明与fBm相比,fLm条件下lnK的取值范围更广,逐渐偏离均值2.5,尤其是处于较小值与较大值间的范围增加,表明渗透系数的空间变异性更强。这也表明与高斯分布相比,Levy稳定分布能更好反映地质介质中渗透系数场呈现急剧变化的强变异性。
图1为对应的lnK增量(间距为1)的取样点概率密度与理论Levy概率密度函数及理论Gaussian概率密度函数的对比。从图中可看出,取样点概率密度与理论Levy概率密度函数拟合较好。其中与理论Gaussian概率密度相比,理论Levy概率密度函数能较好的捕捉到取样点概率分布的峰值和尾部收缩缓慢的特征。从而证明了通过SRA3DC生成的lnK随机场具有Levy稳定分布的统计特征,即lnK增量符合Levy稳定分布的条件。图2所示为由式(6)~(8)估值得到的不同间距的lnK增量的宽度参数与间距h之间的关系。从图中可以看出,宽度参数估计值与间距在双对数坐标下呈较好的线性关系,其拟合关系式如下:
ln(C)=0.305ln(h)-1.4684,R2=0.9802(9)
这表明利用SRA3DC生成的lnK随机场的宽度参数C与间距h之间满足仿射不变性(见式(4))。同时由式(4)可知斜率代表估计的Hurst数为0.305,与初始设置的Hurst数0.3非常接近。综合以上验证可知,由SRA3DC生成的符合fLm的lnK随机场样本满足fLm的统计特征。
3 结论
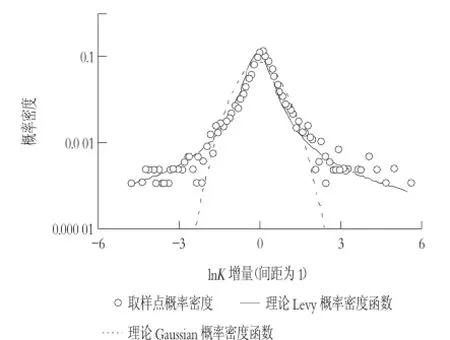
图1lnK增量(间距为1)的取样点概率密度与理论Levy稳定分布及理论Gaussian概率密度函数的比较
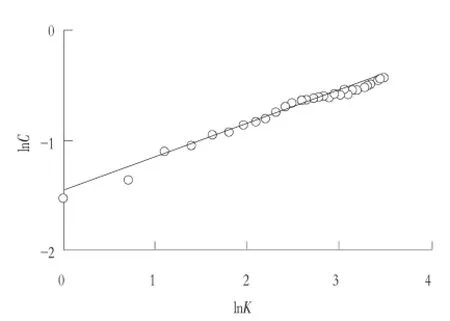
图2 宽度参数C的估计值与间距h的拟合关系
地下水流速的空间变异性是引起地下水污染物不规则迁移的直接因素。因此,正确评估地下水运动过程,对准确预测地下水污染发展趋势并治理地下水污染具有十分重要的理论和现实意义,这其中尤以确定含水层渗透系数的空间分布更为重要。通过利用SRA3DC程序生成了lnK符fBm和fLm的渗透系数随机场,结果表明,符合fBm和 fLm统计特征的lnK随机场表现出不同的空间变异性,其中fLm条件的lnK取值范围更广,空间变异性更强,能更好地反映地质介质中渗透系数场呈现急剧变化的强变异性;通过验证fLm条件下的lnK增量(间距为1)发现:取样点概率密度分布符合Levy稳定分布且宽度参数与增量间距之间的关系满足仿射不变性。此研究还仅局限于渗透系数的无条件生成,但在许多实际工作中,建立在已知部分观测数据基础上的条件生成,及其对地下污染物迁移的影响值得进一步深入探讨。
[1]杨金忠,蔡树英,伍靖伟.宏观水力传到度及弥散度的确定方法[J].水科学进展,2002,13(2):179-183.
[2]DaganG.Modelsofgroundwaterflowinstatistically homogeneousporousformations[J].WaterResources Research,1979,15(1):47-63.
[3]DiFedericoV,NeumanSP.Flowinmultiscalelog conductivityfieldswithtruncatedpowervariograms. WaterResourRes1998,34(5):975-987.
[4]黄冠华,ZhanHong-bin,叶自桐.水力传导度空间变异性的分形模拟研究进展[J].水科学进展,2003,14(2):236-241.
[5]SaupeD.Algorithmsforrandomfractals.In:PeitgenHO,SaupeD(.Eds.).Thescienceoffractalimage[sM].New York:Springer,1988.
[6]VossRF.Fractalsinnature:Fromcharacterizationto simulation.In:PeitgenHO,SaupeD(Eds.).Thescience offractalimage[sM].NewYork:Springer,1988.
[7]LuSL,MolzFJ,LiuHH.Anefficient,three-dimensional,anisotropic,fractionalBrownianmotionandtruncated fractionalLevymotionsimulationalgorithmbasedon successiverandomaddition[sJ].Computers&Geosciences,2003,29(1):15-25.
P641.2
A
1002-0624(2015)10-0044-03
2015-08-01

