光磁相互作用及自旋极化的光学调控

2015-10-31 05:31:08金钻明马红马国宏

物理学进展 2015年5期

关键词：铁磁磁化磁场

金钻明，马红，马国宏*

1.上海大学理学院物理系上海200444 2.山东师范大学物理与电子科学学院山东250014

光磁相互作用及自旋极化的光学调控

金钻明1，马红2，马国宏1*

1.上海大学理学院物理系上海200444 2.山东师范大学物理与电子科学学院山东250014

近年来，超短激光脉冲的发展为人们在极端时间尺度上研究光与物质的相互作用提供了有效工具。皮秒时间尺度上研究磁有序材料中的自旋动力学过程已经成为凝聚态物理研究的热点，促进了自旋电子学的发展。本论文基于飞秒激光抽运–探测技术，介绍了半导体及其纳米结构中光注入自旋极化及其弛豫过程；综述了铁磁性薄膜中的超快退磁，激光诱导磁阻尼进动和逆法拉第效应；利用太赫兹脉冲的磁场分量，研究了反铁磁晶体中自旋共振模式的激发，相干控制以及自旋重取向的探测；最后介绍了超快光谱用于研究多铁性材料中电子、晶格和自旋间的耦合。了解不同材料在超快时间尺度上的磁光、光磁效应的最新进展，有助于在磁有序的超快光控制研究领域做出原创性的工作。

自旋电子学；超快光谱；太赫兹；半导体及纳米结构；铁磁薄膜；反铁磁晶体；多铁性薄膜；超快退磁；逆法拉第效应；相干控制；自旋流

I.引言

20世纪初，施特恩和格拉赫在实验上，首次观察到电子自旋的存在，当时并没有提出“自旋”这一概念[1]。1925年，G.Uhlenbeck和S.Goudsmit根据碱金属原子光谱的双线结构和反常的Zeeman效应，提出了基本粒子的自转与相应角动量概念[2]。63年后，A.Fert等发现巨磁电阻效应（GMR）[3，4]，1991年自旋阀的发明，开启了自旋电子学器件时代。GMR效应的发现解决了制造大容量、小体积硬盘最棘手的弱信号读取问题。根据GMR效应，人们制造出了更加灵敏的数据读头，制作的硬盘存储器容量可以提高三个数量级，这引发了计算机存储的变革。1995年科学家在磁隧道结结构中发现了隧道磁阻效应（TMR）[5，6]，制造出更先进的磁随机存储器（MRAM）。使用这种存储器，数据在断电情况下不会丢失。纵观自旋电子学的发展历程，另一个重要的分支是半导体材料，1990年提出自旋晶体管的概念，2010年已初步实现新概念的自旋量子器件，自旋电子学已经成为国际研究热点领域之一。Albert Fert和Peter Grnberg因发现GMR效应的突出贡献，荣膺2007年的诺贝尔物理学奖。更详细的内容可参阅焦正宽、曹光旱撰写的《磁电子学》[7]。关于铁磁性薄膜的磁性介绍，特别是金属自旋电子学方面的工作可以参阅翟宏如等的《自旋电子学》[8]，韩秀峰等的《自旋电子学导论》[9]。

目前，信息处理过程主要是通过读/写磁头中线圈的电流来实现信息的写入和读取。如果要记录信息，就需要把磁性物质的磁极反转，常用的方式是用外加磁场。与CD-ROM用光束反射率的不同来判断数据是1还是0，磁光效应是通过反射或透射光的“旋转角”来判断反射光随磁化取向不同而产生的变化，称为磁光克尔效应或法拉第效应，只要知道此旋转角的变化就可判断数据是0还是1。然而，目前仍存在两个不足，一是磁头的磁感应过程相对较慢，限制了数据的读写速度；二是磁介质的存储密度受到磁性颗粒大小的限制[10]。光辅助磁光介质存储技术，使用激光热辅助手段将数据记录到具有高稳定性的介质上，随后快速冷却，使已写入的数据变得稳定。由于并不能够脱离读写磁头，读写速度和磁介质存储密度的提高受到限制。此外要求激光对“写入位”加热而对周围“记录位”又不能产生影响，所以激光束必须满足苛刻的空间限制条件。磁介质中信息的存储速度不断提高的需求，电流产生磁场脉冲固有极限的突破等都激发人们通过“非磁场”的方法，去实现电子自旋的操控[11∼13]。

1996年Beaurepaire和Bigot等利用60 fs的激光脉冲实现了镍薄膜中亚皮秒的退磁过程[14]。在随后的近20年里，自旋的“超快光学控制”逐渐成为凝聚态物理一个既充满挑战，又极具争议的研究领域[11]。

根据材料体系的不同，本文综述了飞秒激光在半导体及其纳米结构、铁磁薄膜、反铁磁单晶和多铁性薄膜等四类材料体系中实现电子自旋的激发，探测与控制。超短脉冲对自旋的探测与控制已经对未来自旋电子学的发展起到重要的作用。

II.基本概念及研究进展

A.半导体及其纳米结构中自旋极化弛豫动力学

目前，以荷电性为基础的传统半导体电子器件的运行速度和集成度仍然以摩尔（Moore）律蓬勃发展。但是，随着器件尺寸的不断缩小，量子效应越来越明显，并严重地制约着传统电子学的发展，因此必须寻找传统电子学器件的替代品，自旋电子学便应运而生。半导体自旋电子学是一个由多学科交叉形成的新兴领域，主要研究如何有效地操作/控制半导体及其纳米结构中电子自旋自由度，以期在器件设计中利用自旋自由度结合或替代电荷自由度制备新一代电子器件[15，16]。自旋器件能否实现应用，很大程度上取决于自旋的注入效率、输运距离以及弛豫时间等参数。

1.光学取向注入自旋

自旋注入方式根据注入方法的不同分为光学注入（光学取向）、电学注入、外加电场或者磁场和自旋霍尔效应等方法。本文主要介绍光学取向方法的基本概念。

光子不能直接与自旋自由度耦合，但可以实现电偶极跃迁。利用大多数晶体中都存在的自旋–轨道耦合，可以实现净自旋布居。比如，闪锌矿型半导体材料，导带底s态的轨道角动量为0，而价带顶p态的轨道角动量为1。通过电偶极跃迁，圆偏振光子将改变在光传播方向上的角动量投影，大小为1。假设三个价带（重空穴，轻空穴和自旋分裂带）上的动量在能级上是分离的，比如量子阱或者量子点等低维半导体结构。那么通过与光子能量的耦合，可以实现重空穴到导带的跃迁，重空穴的总角动量是3/2，投影角动量是+3/2或−3/2。轨道角动量和自旋角动量是平行的，即轨道角动量是+1，自旋角动量为+1/2或者轨道角动量是−1，自旋角动量为−1/2。因此，通过自旋–轨道相互作用，轨道的跃迁选择定则转换成自旋选择定则，最大的自旋极化率为100%。

对于半导体块体材料（重、轻空穴带在价带顶是简并的），由于自旋分裂带（J=1/2）具有不同的能量，仍然可以激发自旋极化。以II-VI族直接带隙化合物半导体CdTe为例，如图1所示。价带有3个两重简并的子能带，重空穴带，轻空穴带和自旋分裂带（|1/2，±1/2⟩），重空穴带和轻空穴带在k=0处重合，导带的最低能级有一个两重简并的能带。当用光子能量略大于带隙（Eg＜E＜Eg+∆，∆为自旋分裂带能）的左旋圆偏振光（σ−）激发，由跃迁选择定则可知，允许的跃迁为重空穴跃迁和轻空穴跃迁；同理，对于右旋圆偏振光（σ+）同时激发重空穴跃迁和轻空穴跃迁。根据跃迁选择定则，重空穴态的跃迁几率是轻空穴态跃迁几率的3倍，由重空穴带跃迁与轻空穴带跃迁产生的电子自旋方向是相反的，当用左旋或右旋圆偏振光同时激发重空穴与轻空穴跃迁时，就会分别在导带中产生50%自旋向上或向下的净自旋载流子布居。值得注意的是，光子能量不能高于自旋分裂带，即Eg+∆，因为由重空穴带、轻空穴带和自旋分裂带到导带的跃迁几率比为3∶1∶2，如果激发自旋分裂带，则不能实现电子自旋的光注入。利用圆偏振光光子的角动量选择激发某一取向的自旋电子，称为“光学取向”[17]。

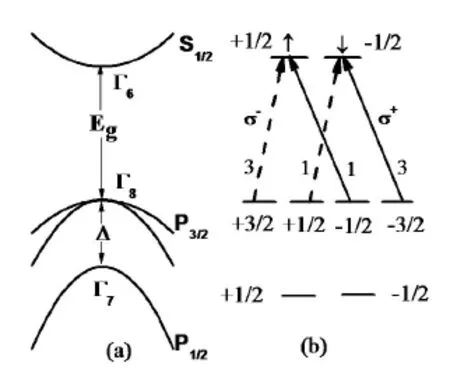
图1.体材料中的选择跃迁定则。图(a)是CdTe的能带结构，(b)图是左旋σ−（虚线）和右旋圆偏振光σ+（实线）的选择性跃迁，并标出了跃迁几率。

2.自旋相干时间

相干态是指在初始时刻系统中所有电子的状态（比如：自旋或轨道）是一致的，随着时间的演化，电子的状态保持一致地变化，这时的电子态称为相干态。在描述电子自旋相干态之前，首先介绍一下半导体中电荷相干态。在一个孤立的量子体系中，波函数Ψ满足薛定谔方程[18]：

其中H是系统哈密顿量，它通常包括系统、环境和它们之间的相互作用三个部分。一般考虑二能级系统与光场的相互作用。设二能级系统的波函数为：

其中a和b分别为激发态和基态的振幅。设在t= 0时系统处于基态，即a=0，b=1。从t=0开始，施加一个光场E，则电子与光场的相互作用哈密顿量写为：

设H对能级能量的影响很小，可以忽略，则（1）式改写为：

由（5）式可见，如果一个量子体系只与光场相互作用，则电子将在两个态之间振荡，振荡频率为：

这一频率称为拉比（Rabi）频率。振荡的一个周期内，系统经历了从光场吸收能量又还给光场的过程。对于半导体等实际材料体系，是由许多单个二能级体系组成的系综。如果在t=0，所有体系都保持相同的振幅a和b，并且所有体系的a和b都按照相同的规律（5）式随时间变化，这就是电荷的相干态。由于电子–电子相互作用，相干态只能维持一定的时间，这一持续时间称为退相时间。

现在考虑一个单自旋系统，具有自旋态+1/2，因此它的波函数是一个二分量函数，类似于（2）式，a和b分别代表自旋为+1/2和−1/2的振幅。磁场下自旋系统的哈密顿量为：

其中µ0是电子磁矩，g是半导体中电子的朗德因子，σ是泡利矩阵：设自旋的初态沿着垂直于磁场的方向，设为z方向，则自旋波函数的初始条件为a=1，b=0。磁场沿y方向，H=−µ0gBσy。代入薛定谔方程，得到：

解方程（9）式，并考虑波函数初始条件，得到：

如果将a和b看作是一个在垂直于磁场平面内的矢量的两个分量，则这个矢量将随时间在平面内转动，自旋绕磁场的运动称为拉莫尔（Larmor）进动，进动的频率为

图2.自旋弛豫过程中的(a)纵向弛豫时间T1和(b)横向弛豫时间T2示意图。

自旋布居的演化有两个不同的自旋相干寿命。非相干的纵向弛豫时间T1，描述的是两个自旋态上布居数的改变，如图2（a）所示。横向弛豫时间T2是相干的。若自旋的取向垂直于磁场，即包括了两个相等的，平行和反平行于外加磁场的自旋态布居，他们之间有一个特定的相位。这一相位相干的衰减过程反映了垂直于外加磁场自旋极化的衰减，如图2（b）所示。值得注意的是，相位的相干衰减并不影响两个自旋态的布居情况。纵向和横向弛豫时间之间最大的区别在于：纵向弛豫时间涉及布居数变化，与系统的能量相关；横向弛豫过程不涉及能量。

半导体中的自旋极化电子是由许多单个电子自旋态所组成的系统，自旋相干态就是指所有电子都以同一个频率进动。由于自旋–自旋，或者自旋–杂质、自旋–声子间的相互作用，系统的总自旋（磁化强度）将随时间呈现指数衰减：

在原子核系统中，由于能量从自旋系统转入或转出相当困难，这一能量瓶颈预示T1和T2有几个数量级的大小差异。然而对于块体或者量子阱半导体系统，则没有这个能量瓶颈。

3.实验技术

a.时间分辨光致荧光光谱技术

电子自旋研究的初期，主要的研究方法是光致自旋荧光测量法，这种方法基于自旋极化向上和向下的电子辐射复合时分别发出左、右旋圆偏振光。借助四分之一波片和偏振片，用条纹照相机可分别获得时间分辨的左、右旋圆偏振光强度，从而得到发光的圆偏振度。基于电子自旋极化度与所发光的圆偏振度相同的基本假设，则可获得电子自旋极化偏振度。起初这种技术只能计算电子自旋的偏振度，不能得到动态的弛豫过程。基于条纹相机和上转换技术的时间分辨光致荧光法，能成功探测初始自旋偏振度和自旋极化载流子荧光偏振度的时间演化，被用于电子自旋动力学的实验研究。1980年，Alfano等基于此技术，实验测得Zn∶GaAs（Zn的浓度为7×1017/cm3）在77 K时，电子的自旋弛豫时间常数为88±34 ps[20]。由于光致荧光要求激发态自旋偏振电子有大的辐射复合概率，一般材料在常温下的荧光效率很低，因此实验测量通常需要在低温下进行，以提高辐射复合概率，增加发光效率。这就限制了常温条件下电子自旋弛豫时间的研究。

b.圆/椭圆偏振光抽运探测透射/反射光谱技术

以超短激光脉冲为光源的抽运-探测技术是研究材料超快动力学的基本手段之一，可以获得激发态随时间演化的信息。1990年Tackeuchi等首次通过圆偏振光激发和探测自旋载流子的密度变化来研究电子自旋，室温下测得GaAs/AlGaAs多量子阱中的电子自旋弛豫时间为32 ps[21]。这种光谱技术使用左、右旋圆偏振光分别测量自旋极化向上和向下的电子数布居弛豫，从而获取电子自旋极化弛豫时间常数[22−24]。一束强圆偏振光激发材料在相应的激发态上实现自由电子布居，这些电子会通过各种途径离开激发态，从而减少激发态布居，受激发电子布居的变化与材料的光电子特性密切相关。用另一束较弱的圆偏振激光脉冲（探测光）去探测这个变化，可以反推出激发态的信息，逐步改变探测光和抽运光的时间延迟就可以得到激发态随时间演化的整个过程。如果采用圆偏振的脉冲激光，光子的角动量是±1，根据光学取向原理，可激发净自旋极化，就可以得到自旋弛豫动力学过程。当改变探测光的旋向，实现抽运光和探测光的旋向相同或相反，重复扫描光谱，即完成同向圆偏振和反向圆偏振抽运–探测光谱，两条曲线的差值可以去除热电子弛豫信息，仅留下自旋弛豫过程。

Lai等进一步发展了抽运探测技术，用椭圆偏振光代替圆偏振光，形成椭圆偏振光吸收量子拍光谱技术[25∼27]。利用这一技术测量了GaAs及其量子阱中的自旋极化、相干与弛豫过程。另外，还发展了圆二色吸收差分谱，得到n−GaAs体材料的自旋扩散常数为Ds=201±25 cm2/s[28]。

c.时间分辨法拉第/克尔旋光技术

早在1845年法拉第在探索电磁现象和光学现象之间的联系时，发现当一束平面偏振光穿过沿光的传播方向加有磁场（B）的介质时，观察到光经过样品后偏振面转过一个角度θF，见图3，亦即磁场使介质具有了旋光性，这种现象称为法拉第效应。法拉第效应中的磁场可以是外加磁场，也可以是有效磁场。在半导体及其纳米结构中，Awschalom提出圆偏振光通过光学取向诱导有效磁场，当另一束强度较弱的线偏振探测光透过材料后其偏振面会发生偏转，透射光偏振面的偏转角称为Faraday旋光角（反射光偏转角称为Kerr旋光角）[29∼31]。其本质是右旋和左旋圆偏振光在介质中的折射率不同，即η+̸=η−，旋转角的大小与右旋和左旋圆偏振光在材料中的折射率之差成正比[32]。

研究表明，当材料是非磁性半导体材料时，偏转角要比稀磁半导体小1到2个数量级。实验中要探测的信号是由抽运光引起的探测光偏振面偏转角度的微小变化，大约在10−4度的量级。如何将如此微弱的信号取出，是实验光路设计的难点。为此必须用光学平衡桥检测电路，来消除激光强度和偏振噪声的影响，并使用锁相放大器进一步提高信噪比。

除了以上三种常用方法测量自旋弛豫时间之外，还有Scholes等最近发展的超快偏振瞬态门技术，利用这种技术测量了多种半导体材料的自旋动力学[33，34]；另外还有适合测量异质结的自旋极化的抽运–探测二次谐波技术[35]等。

图3.时间分辨的磁光法拉第效应示意图。圆偏振光抽运，线偏振光探测样品。

4.电子自旋弛豫机制

目前半导体中电子自旋弛豫机制主要包括DP（D’yakonov-Perel’）机制[36]，EY（Elliott-Yafet）机制[37，38]，BAP（Bir-Aronov-Pikus）机制[39]。DP机制源于中心反演不对称系统的自旋–轨道相互作用，它使得导带的自旋分裂，这一分裂相当于存在一个与波矢k有关的有效磁场，有效磁场驱使自旋进动。EY机制是指，存在晶格和自旋–轨道耦合相互作用的情况下，精确的Bloch态不是自旋的本征态，这就引起了一个有限的自旋翻转几率。由于电子–空穴之间的交换作用而产生的自旋翻转散射导致的自旋弛豫机制称为BAP机制。在本征半导体体材料中，空穴的弛豫比电子快的多，约100 fs，所以不考虑BAP机制。这些机制的相对重要性随着材料本身的性质、温度和浓度等因素而不同，因此实验过程中观察到的现象丰富多彩。

5.研究进展

自旋弛豫的研究从上世纪50年代开始，大多数研究集中在Ⅲ-Ⅴ半导体中。因为在这些材料中通过光学手段可以直接测量自旋弛豫时间，例如GaAs[40]、p-GaSb、GaAlAs、n-InSb、n-GaAs以及InAs[41−43]。其中Kikkawa等利用时间分辨的法拉第（Faraday）旋转技术测量了GaAs体材料在低温时的自旋弛豫时间[41]。结果表明自旋弛豫时间对电子浓度有非常强的依赖关系，当电子浓度为1×1016/cm3时，自旋弛豫时间达到最长。Kimel等也利用此方法研究了CdTe、GaAs和In-P体材料中的电子自旋弛豫过程[45]，常温下电子的自旋弛豫时间非常短，从几个皮秒到几十个皮秒。

Song等基于先前的实验结果，构造了一个类似相图的图来说明主要的自旋弛豫机制，对不同自旋弛豫机制之间的竞争做了全面的阐释。对几种Ⅲ-Ⅴ族半导体体材料，如p型和n型GaAs、GaSb、InAs、InSb，标记出主要的自旋弛豫过程与温度和杂质浓度的函数关系。结果发现，对p-GaAs和p-GaSb得到的相图定量地与以前的结果一致。但在低温下，n-GaAs理论结果与实验结果存在很大差异。在实验中，5 K时ND=1016/cm3的条件下，τs≈100 ns，而DP理论预言ns[46]。在这样低的温度范围内，自旋弛豫应该主要源于EY机制[47]。然而，根据动量弛豫时间τp≈1 ps，得到，DP机制和EY机制都不能很好地解释实验结果。理论与实验不符合的原因可能来源于忽略了电子与核的超精细相互作用。但是Dzhioev人测量了n-GaAs在4.2 K时束缚电子的自旋时间，观察到了290±30 ns的结果，还是不能和理论符合[48]。最近考虑了所有的散射机制的微观动力学布洛赫（Bloch）方程方法[49]，对上述理论进行了修正，很好地解释了实验结果。

Ma等研究了CdTe和InP本征体材料[50，51]的自旋弛豫时间τS与载流子浓度的依赖关系，首次观察到本征体材料的自旋弛豫寿命τS随着载流子浓度的变化是非单调的，随着载流子浓度的增加，自旋弛豫时间常数先增加，到达最大值后再减小，如图4所示。由图4（a）可知室温下CdTe单晶的自旋弛豫寿命只有几个皮秒，相比InP单晶的寿命更短。在70 K时，InP的激发浓度为1.376×1017/cm3时，自旋弛豫最慢，寿命最长，达到2164 ps。常温下自旋弛豫时间随载流子浓度的变化和低温的趋势相同，但是峰值浓度却明显不同，常温下峰值浓度为2×1017/cm3，大于低温的峰值浓度，如图4（b）。因此自旋寿命的转折点与温度有关，温度越高自旋寿命的最大值所对应的光生载流子浓度越高。实验结果证实了基于全微观动力学自旋布洛赫方程方法对半导体中电子自旋寿命的预测，表明本征半导体中的电子自旋寿命主要由DP（D’yakonov-Perel’）机制决定。

除了半导体体材料之外，稀磁半导体中电子自旋过程也是的研究热点。赵建华等的综述文章对磁性半导体做了详尽的介绍[52]。Crooker等[53]最早利用时间分辨的Faraday旋转技术研究了掺Mn2+的磁性半导体量子阱中的自旋极化。他们分别观测了空穴、电子以及Mn2+的自旋信号随着时间的演化：空穴极化很快完成弛豫，而Mn2+却可以持续几百皮秒，电子的弛豫寿命在几十皮秒量级。理论上通过建立Bloch方程[54]给出了Faraday旋转角和自旋相干的关系，很好的描述了他们的实验。在掺Fe的InP中，法拉第旋转角实验结果表明与自旋有关的弛豫过程持续几百皮秒，随激发强度的增加而变长[55]。

在低维半导体材料中，由于强量子限制效应引起的准连续能级分裂为类分子的分立能级，导致自旋弛豫寿命变长。Ohno等利用光致发光方法得到了GaAs（110）量子阱中自旋弛豫时间长达几个纳秒[56]。Sogawa等采用光致荧光光谱研究了GaAs/AlAs量子线的自旋弛豫过程，发现一维结构的材料具有比同类量子阱和体材料有更长的自旋弛豫时间[57]。常温下ZnO量子点中的电子相时间达到25 ns[58]。He等利用超快偏振瞬态门技术测量了CdTe/CdSe核/壳结构量子点0中自旋的弛豫过程，结果表明壳的厚度从0.2 nm增加到2.0 nm过程中，空穴的弛豫时间从0.3 ps增加到10 ps。这是因为当壳层的厚度约为1.2 nm时，量子点从Ⅰ类转变成了Ⅱ类，在Ⅱ类量子点中实现了电子和空穴的分离，从而抑制了电子–空穴交换相互作用，最终使得空穴的弛豫时间变长[33]。Ruan等利用时间分辨克尔技术研究了GaAs/Al0.35Ga0.65As异质结，温度从1.5 K增加到30 K的过程中，自旋弛豫时间表现出了非单调性，在14 K时达到最大值3.12 ns[59]。

图4.自旋弛豫寿命随激发载流子浓度的变化。(a)CdTe单晶，激发光子能量为1.485 eV，温度为室温。(b)InP单晶，(■)线表示室温，(⋆)线表示70 K，激发光子能量为1.393 eV。

Zhang等研究了II-VI族半导体量子点自旋与量子点尺寸的关系[60]，Feng等对CdS凝胶量子点进行了光学操控，线偏振的预抽运光有效提高了电子自旋相干信号，控制光有效抑制了电子自旋相干幅度，发现抑制强度与光的旋转特性无关[61，62]。Ma等利用圆偏振抽运探测光谱研究了CdSe凝胶量子点。研究结果表明激子自旋寿命与量子点的尺寸密切相关，对于大尺寸的量子点，激子自旋寿命表现为几个皮秒的单指数过程，该过程是由空穴的自旋反转所引起的；而对于尺寸较小的量子点，其激子的自旋寿命存在两个过程，一个是几个皮秒的快过程，另一个为纳秒量级的慢过程。研究证实了快过程是空穴的自旋反转过程，而慢过程为电子自旋反转的结果。空穴自旋反转可以用激子的带间跃迁来描述，电子自旋的反转可由激子的带内跃迁表述[63]。利用法拉第旋转光谱还研究了水溶性CdTe量子点的瞬态磁光响应，值得一提的是，在水溶性CdTe量子点中首次观察到瞬态磁光法拉第效应由抗磁向顺磁演变的光谱学行为[64]。

最近，有机无机杂化钙钛矿结构CH3NH3PbI3薄膜中的自旋极化得到了研究，样品厚度约70 nm，带隙为1.6 eV，其带隙结构和常规III-V族、II-VI族半导体不同，不考虑自旋轨道耦合时，CH3NH3PbI3属于直接带隙半导体（R点），导带为6重简并（总角量子数J={1/2，3/2}，L=1），价带为双重简并（J=1/2，L=0）[65]。考虑自旋轨道耦合时，导带分裂为2个态，导带底为双重简并态（J=1/2），距离价带顶（带隙）为1.6 eV，和一个能量较高的四重简并的态（J=3/2），距离价带顶为2.8 eV，价带结构基本不变。mj=+1/2态由33%自旋向上态和67%的自旋向下态组成，而mj=−1/2态由67%自旋向上态和33%自旋向下态组成。如图5所示，CH3NH3PbI3的自旋弛豫寿命较短，即使在77 K低温下，电子自旋弛豫寿命只有约7 ps，空穴只有约1 ps，但是这种材料具有超大的法拉第旋转角，200 K时旋转角达到最大值10◦/µm，这些研究表明CH3NH3PbI3在自旋光开关方面具有广阔的应用前景，是一个崭新的研究方向[66]。

图5.(a)CH3NH3PbI3的法拉第旋转角与延迟时间的函数，抽运光分别是左旋圆偏振光（红色），右旋圆偏振光（蓝色）和线偏振光（品红）；(b)最大旋转角度随温度的依赖关系，摘自文献[66]。

对半导体自旋电子学领域想要有更系统和深入的了解，可以参阅科学出版社出版的夏建白、葛惟昆、常凯编写的《半导体自旋电子学》[67]；和姬扬翻译的由迪阿科诺夫主编的《半导体中的自旋物理学》[68]。

B.过渡金属及合金薄膜中光磁动力学

从大功率变压器，传感器到数据存储和自旋电子器件，具有巡回特性的金属铁磁体有着众多的应用前景。超快磁动力学起步于看似简单的金属铁磁体，如：Ni、Co、Fe、Gd等[69−71]。光子能量首先注入到电子和晶格系统。磁化动力学的时间尺度由内部的平衡过程所决定，包括电子–电子、电子–声子和电子–自旋相互作用。对于过渡族铁磁材料来说，退磁过程短至约50 fs。退磁寿命也受到外部参数，如衬底的热导率，样品的几何形状等的影响。尽管取得了很多重要的结果，但无论是实验还是理论，都还存在着争议[72，73]。

1.三温度模型

1996年，Beaurepaire等用60 fs的激光脉冲，首次成功得到了22 nm厚Ni薄膜的瞬态透过率和时间分辨的磁光克尔效应，并通过唯象“三温度”模型定性解释了这一超快退磁过程，如图6所示[14]。从瞬态反射率估算电子的热化时间约为260 fs，电子的温度衰减常数为1 ps。自旋温度可以通过时间分辨的磁滞回线估算，在2 ps左右达到最大值。电子和自旋有着不同的动力学行为[74]，退磁过程中还会有太赫兹辐射，如图7所示。

图6.飞秒激光脉冲(60 fs)激发后，Ni薄膜的剩磁关于时间的函数，摘自文献[14]。

一个简单的模型用来描述退磁过程中复杂的相互作用[11]，包含三个各自独立但又相互关联的体系，即电子、晶格和自旋，称为现象学“三温度模型”。它描述了三个自由度耦合的时间演化，从唯象角度定性描述“退磁过程”[11，14]：

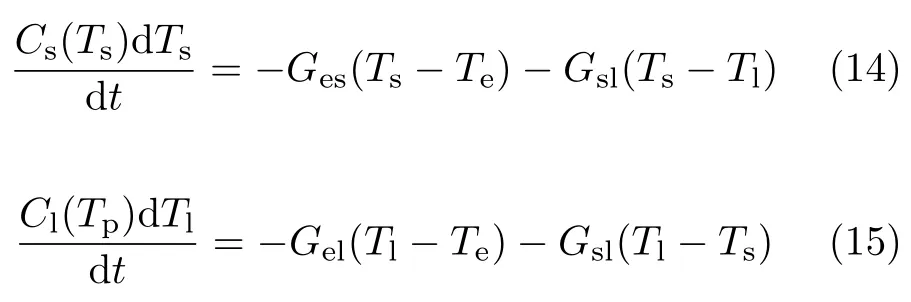
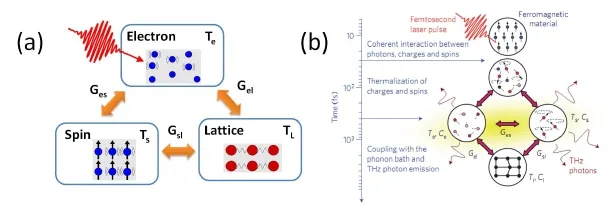
图7.(a)唯象三温度退磁模型，(b)超快退磁过程伴随有THz波辐射，摘自文献[74]。

其中，Ce、Cs和Cl分别代表电子、自旋和晶格的比热容，Gel、Ges和Gsl分别是电子–声子、电子–自旋和自旋–声子耦合的唯象系数，能反映体系间的相互作用强弱，但不能用于解释相互作用的本质。Ti代表相应系统的温度，P（t）表示光子能量的注入。由于电子的热容比晶格的小一到两个数量级，因此电子温度在激发后的几十飞秒内就达到几千开尔文，此时晶格仍相对“较冷”。

“三温度模型”发展于描述金属及其纳米结构中的热电子动力学的“二温度模型”[75，76]。在光频区，只有电子能响应电磁场的激发，同步地吸收或散射光子。

1.光子能量被铁磁系统吸收后产生高能热电子，这一过程的时间尺度为1 fs左右；

2.这些热电子通过电子–电子相互作用，在约50∼500 fs内形成费米–狄拉克分布，且具有热平衡电子温度Te；

3.热电子通过声子级联过程弛豫，弛豫时间决定于电子–声子相互作用时间（对金属而言，在100 fs∼1 ps左右），同时热化声子，使晶格温度升高至Tl。

在约1∼2 ps内，电子和晶格系统达到热平衡，如图8（a）所示。

半金属具有特殊的电子能带结构，既有金属行为，又包含半导体行为（具有能隙结构）的材料体系。激光诱导半金属的退磁研究能揭示其电子能带结构和自旋动力学间的联系。2000年，Kise等研究了半金属铁磁体Sr2FeMoO6中约500 ps的自旋弛豫，这一慢过程归结为半金属的本征特性。半金属中自旋与电子和晶格体系存在“热隔绝”[77]。2006年，Zhang等在半金属CrO2中观察到相似的慢退磁过程，解释为自旋和电子间不存在相互作用[78]。2009年，Mller等系统研究了半金属材料体系退磁时间和费米能级处自旋极化（45%∼98%）之间的联系，如图8所示[79]。

除能量外，磁化的本质是角动量，在磁性系统中，需要考虑角动量守恒。在退磁过程中，自旋系统必将损耗掉一定量的角动量。因此，当涉及超快退磁过程时，揭示角动量转移的途径是至关重要的。通常来说，电子和晶格系统都会吸收角动量，自旋–晶格相互作用和磁晶各向异性能通常是在同一数量级上。过渡金属的磁晶各向异性能相当弱（约为100µeV），这起源于晶体场诱导电子轨道的猝灭。因此，可以预见相应的相互作用时间会相当长，在Ni中约为300 ps[80]。然而，超快退磁过程清晰地表明金属中，自旋和其他系统间存在更强的耦合，Elliot-Yafet自旋反转散射可能是导致自旋系统温度快速上升的原因[81，82]。Elliot-Yafet散射过程起源于自旋–轨道耦合，导致的电子自旋向上和向下态的带混合。如图8（a）所示，激光脉冲升高了电子温度Te后，瞬间同时增加了自旋系统的温度，时间尺度在几百飞秒。尽管“三温度模型”可以成功地定性解释超快退磁，估算电子–声子热化时间和退磁时间。电子–自旋或者声子–自旋耦合对解释小于100 fs的超快退磁仍是目前学术界争论的主题。争论主要集中于退磁过程中，角动量的守恒。如图9所示，Malinowski等在Co/Pt多层膜中研究了自旋角动量在层间的转移可以加速退磁过程[83]。通过飞秒激光产生自旋流所诱导的自旋转移力矩提供冲力，来控制磁化。具体的做法是使用磁多层膜结构，第一层铁磁膜直接受光脉冲激发或者来自于周围非磁性材料中的热电子作为自旋流的源；第二层铁磁层则用来探测自旋流[84]。Schellekens[85]和Choi[86]两个小组都观察到了第二层铁磁膜的磁化旋转，这是激光诱导自旋流产生自旋转移力矩的标志。

图8.(a)超短激光脉冲激发后，电子、晶格和自旋温度的时间演化过程。自旋温度的演化过程选取了两种情况，一是在金属中的强耦合（点线），二是在介电材料中的弱耦合（虚线）。(b)全光抽运–探测实验获取退磁时间，尽管Ni和哈斯勒合金Co2MnSi表现出快退磁过程，半金属材料Fe3O4、CrO2和LaSrMnO3的退磁过程，其退磁时间τm要慢2个数量级以上，摘自文献[79]。

图9.(a)实验构置分别代表反平行和平行状态。(b)异质结构处于磁化平行（红色圆圈）和反平行状态（黑色圆圈），隔绝层分别为NiO(1.2 nm)和Ru(0.4 nm)，曲线在电子热化后的3 ps处归一化，摘自文献[83]；(c)超快自旋转移力矩示意图，初始（最终）磁化矢量用黑色箭头表示，摘自文献[84]。

2.磁化矢量的动力学

磁化矢量与外磁场的相互作用是理解磁现象的基础。对于均一的固态磁体，M=Vm，其中M是磁化矢量。如果V是原子体积，那么m是单位原子体积的磁矩；如果V是磁性材料的体积，那么M是材料的总磁矩。对于非均一的情况，磁性固体可以被分割成若干小区域，每个小区域里的磁矩被认为是均一的。若这些区域足够大，则磁化运动仍可以认为是经典的。在没有阻尼的情况下，磁矩的进动可以通过转矩方程来描述。根据量子理论，角动量与磁矩M的关系[8]：

其中γ是旋磁比。磁矩M在外场H作用下，经历一个转矩：

从基本的角动量守恒定则可以得到自旋在外场中的运动：

上式表明，磁动量随时间的演化与外场和磁矢量本身都垂直，因此磁矢量将绕着外场进动，进动频率是外磁场的线性函数。当磁矩不仅受外场的作用，还受到磁晶各向异性，形状各向异性等的影响，情况就更加复杂。所有这些相互作用都将对热动力学势ϕ产生贡献。方便起见，可以用一个有效磁场来综合考虑这些影响：

因此，磁化矢量的动力学方程可以改写成：

其中Heff包括了许多贡献：Heff=Hext+Hani+ Hdem+···，其中Hext是外磁场，Hani是各向异性场，Hdem是退磁场。除了外磁场，其他的贡献均与材料性质密切相关。

其中α是无维的Gilbert阻尼系数，通常包含本征和非本征两项。本征系数α0源自于自旋–轨道耦合。非本征阻尼系数常在薄膜和异质结构中，来自非局域自旋弛豫过程，导致了α系数增加[87]。Gilbert阻尼项用来解释磁激发能量的弛豫过程。相干进动是目前所知最快的改变宏观磁化方向的方式。

图10.磁矢量进动动力学示意图：(a)M的初始态沿着平衡方向Heff；(b)有效磁场的方向发生突变Heff→He′ff，导致磁矢量绕着新的有效磁场进动；(c)由于阻尼M最终停留在新的平衡位置。

超快光诱导磁化的改变提供了研究磁进动的实验方法。当飞秒光脉冲激发磁性材料时，通过光诱导材料相关场的改变，导致光诱导磁动力学，M开始绕着新的有效场H′eff进动，如图10所示。外磁场应施加于接近“难磁化轴”方向，目的在于使得各向异性场、退磁场和外磁场呈现“非共线”几何构置。磁化处在某一平衡位置，它是各向异性场、退磁场和外磁场共同作用的结果；激光诱导的温度改变和磁化的改变会导致磁晶各向异性和/或形状各向异性发生变化，从而形成新的平衡位置。如果这一改变比相应的磁进动周期快，那么磁矢量将绕着新的平衡位置进动，最终由于热扩散重新回到最初的平衡位置。

图11.Ni薄膜亚皮秒的退磁过程(τm)，通过电子–声子弛豫(τE)回复，当延迟时间大于100 ps可以观察到磁进动阻尼过程(τLLG)，摘自文献[88]。

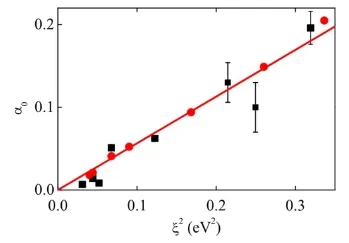
图12.L10FePd1−xPtx有序合金中对于不同的x，实验（实心方块）和理论（实心圆圈）所得的本征阻尼系数α0随自旋–轨道耦合强度的变化，实线为正比函数拟合，摘自文献[89]。

Koopmans等提出的微观模型成功解释铁磁金属中磁化矢量的超快回复过程，并发现退磁时间τm与Gilbert阻尼系数α间的联系τm≈ħ/kBTcα，将亚皮秒的磁响应归结为声子调制的自旋反转散射，如图11所示[88]。He等人系统研究了L10FePd1−xPtx有序合金在不同外加磁场下的磁化动力学过程，发现Gilbert阻尼系数随着Pt含量的增大而增大，解释为材料体系中的自旋–轨道耦合强度ξ的加强，如图12所示[89]。非本征阻尼系数可以通过设计缓冲层，覆盖层等来调节[90]。Zhao等利用时间分辨的磁光克尔技术系统研究了庞磁阻锰氧化物LaCaMnO3的自旋动力学，在时间维度上给出了各向异性和阻尼等量化信息[91−93]。

3.研究进展

a.特定元素退磁的探测

随着研究的深入，新的磁化动力学研究方法：时间分辨的X射线磁圆二向色性（XMCD）被用于研究自旋的反转，其优点在于对不同化学元素的“专一性”探测[94]。用能量为66 eV的X-射线脉冲探测被1.6 eV光照射下的铁磁样品，可以区分电子的荷电和自旋自由度，抽运和探测脉冲的偏振都在入射面内（入射光和出射光所组成的平面）。通过改变抽运–探测脉冲的时间间隔，可以勾勒出铁磁薄膜的退磁时间。如图13所示，Gd和Fe离子亚晶格的剩磁在光激发后迅速塌陷，各自的磁化方向快速反转，两套亚晶格在各自不同的时间尺度上重建剩磁。Radu等发现1.5 ps内，Gd完成了反转，比Fe的反转慢300 fs。因此，尽管这个材料的基态是反铁磁耦合的，在磁反转过程中（0.4 ps）会出现一个Gd和Fe自旋瞬态的平行排列状态，如图13所示[95]。此外，X射线可以克服红外脉冲在空间分辨上的限制。纳米尺度的空间分辨，使得超快自旋研究逐步从“时域”走向“空间”[96]。

时间分辨的X射线圆二向色性还能用于研究每一种元素的自旋和轨道角动量各自的贡献。Bergeard等发现，角动量在两套交换耦合的亚晶格中的局域转移驱动了亚铁磁合金Co0.8Gd0.2的退磁过程，过程中总角动量保持不变；而在Co0.74Tb0.26中，总角动量向外部转移，且延迟了约150 fs[97]。

b.全光磁化反转

获得快速、可靠的磁化矢量在两种磁亚稳态间的转换是现代磁存储技术的关键课题。一种具有潜力的研究方案是用圆偏振飞秒脉冲通过逆法拉第效应实现全光旋性选择的高速磁开关。Stanciu等使用无定形的铁磁合金Gd22Fe74.6Co3.4（GdFeCo）作为研究对象。如图14所示，40 fs的激光脉冲垂直入射到样品表面，所产生的有效磁场将直接沿着激光脉冲的传播方向。不同的偏振光对于初始磁畴有着截然不同的影响：圆偏振光扫描时，被扫过的区域显示为由左旋光产生的“向上”和右旋光产生的“向下”的有效磁场所决定的“白”或“黑”的磁畴状态；而被线偏振光扫过的区域则显示为“灰色”，表明磁化方向既有“向上”又有“向下”，说明磁畴处于杂乱的状态。实验结果表明，在没有任何外磁场的条件下，40 fs的圆偏振光实现了全光磁反转[98]。

图13.(a)外磁场H下，Fe和Gd磁化的非平衡动力学示意图，及其(b)时间分辨的XMCD实验测量，摘自文献[95]。

图14.(a)偏光显微镜下，GdFeCo合金的磁化“向上”和“向下”的磁畴分别对应于观察到的“白色”和“黑色”区域；(b)右旋(σ+)，左旋(σ−)和线偏振L三种不同偏振的光脉冲对合金GdFeCo进行扫描，摘自文献[98]。

值得注意的是，Vahaplar等发现这一磁化反转发生于一个相对较窄的激光强度范围。当光强低于某一值时，激光不能诱导磁化反转，然而当强度超过某一值后，两种旋性的光都能导致磁化翻转[99]。实验和理论工作都表明，不使用外加磁场，单纯使用激光脉冲的“热量”也能颠倒磁极[100，101]。Ostler等认为GdFeCo中全光磁化反转的关键是两套不相等的磁亚晶格，与激光的偏振无关，而是由于稀土和过渡金属具有不同的退磁时间。并将先前所发现的圆偏振依赖的全光磁开关归结为磁圆二向色性，即吸收光子能量的多少取决于光的偏振。Satoh等通过调节抽运脉冲的聚焦特性，实现了形状不同的自旋波源，最终能控制自旋波的辐射方向[102]。全光磁反转实验表明，光子学在自旋电子学中扮演了重要角色。对于超快磁过程的光学激发和探测，姬扬翻译的由史拓和希格曼主编的《磁学–从基础知识到纳米尺度超快动力学》具有极高的参考价值[103]。

c.超快退磁与THz辐射

激光诱导超快退磁的另一个特点是辐射THz波。当铁磁薄膜的磁化矢量Mx在亚皮秒时间尺度上发生变化，根据Maxwell方程，远场辐射的电磁波Ey（t）∝∂2Mx/∂t2，携带丰富的自旋信息。2004年，Beaurepaire等首次观察到Ni薄膜中有THz发射，如图15所示[104]。Hilton等的实验结果表明Fe薄膜中的THz发射有两部分贡献，一是与抽运光偏振有关的非线性光整流效应，另一个是与抽运光偏振无关的起源于超快退磁的部分[105]。Shen等发现THz电磁脉冲的幅度正比于铁磁薄膜的Gilbert阻尼系数[106]。

2012年，Kampfrath等实现对铁磁/非磁金属薄膜异质结构中，飞秒激光诱导的“自旋流”脉冲的有效调控[107]。具体的，借助于铁磁材料能带结构的自旋相关性，光激发的多数自旋电子能跃迁到迁移率高的能带，而少数自旋电子则跃迁到迁移率较低的能带。这一非对称光激发，能产生非零的扩散自旋电流。逆自旋Hall效应（自旋–轨道耦合使电子偏离）使得自旋流转换成横向电荷电流，作为太赫兹电磁辐射源，如图所示。通过裁剪异质结构，比如选择低迁移率（Ru）或者高迁移率（Au）作为覆盖层，可以有效调控飞秒光所诱导的“自旋流”，从而改变THz辐射的形状，如图16所示。

THz发射光谱可以作为一个有效的自旋电流探测器。在未来自旋光电子集成电路中起到快速且非破坏性的表征作用。材料不局限于金属，可以是稀磁半导体[109]，强关联过渡金属氧化物和超导材料等。

图15.THz产生于激光热化的Ni薄膜，(a)中的光滑曲线来自于假设如(b)所示的磁化随时间演化过程与高斯函数的卷积，摘自文献[104]。

C.反铁磁单晶中光磁相互作用

1.光诱导自旋的瞬态极化

早在1965年，J.P.van der Zie等预言逆法拉第效应的存在，并观察到圆偏振光可以在掺Eu2+的CaF2、一系列抗磁性玻璃、甚至在有机或无机液体等非吸收材料中诱导磁化[110]。随着激光脉冲的脉冲宽度不断的压缩，飞秒激光使得光磁效应在磁有序材料中的强度大大增强。光和电子自旋间直接的相互作用可以从“能量”角度进行推导。在单色光场E（ω）作用下，磁有序材料的热动力学势ϕ包含[8]：

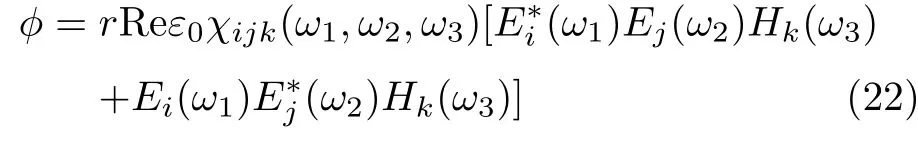
式中χijk表示磁光系数。电偶极近似下，对于光场E（ω），材料的线性光学响应定义为光极化矢量。从（22）中可以看出光极化矢量P（ω）存在正比于磁化矢量的部分：

图16.(a)铁磁异质结构辐射THz脉冲示意图，(b)时域上，从不同结构发射出的两种THz脉冲形状。深色和浅色的线表明，样品的磁化方向相反时，信号发生反转。(c)根据(b)的瞬态电场所得的傅立叶光谱，摘自文献[107，108]。

从上式可以看出，当线偏振光通过磁性介质时，光的偏振方向将发生旋转θF，如图17（a）所示：

式中，c是真空中的光速，n是材料的折射率，L是光在介质中传播的距离。公式（24）所描述的就是Faraday在1846年发现的法拉第磁光效应。

根据公式（22），还可以发现一个频率ω的光场，沿着光波矢的方向产生一个有效磁场，如图17（b）所示：

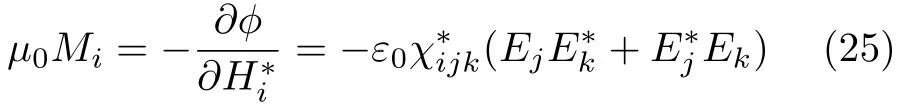
在各向同性材料中，χijk是全反对称张量，可以将

其看成一个独立的张量元χ，上式可改写为：

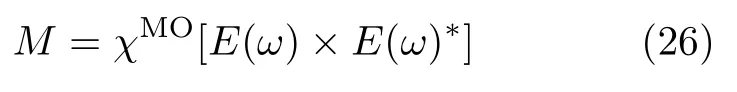
图17.(a)法拉第效应和(b)逆法拉第效应示意图；(c)一种可能的光诱导磁化的微观机制，相干受激拉曼散射示意图。

从（26）式得出结论，右旋圆偏振光和左旋圆偏振光分别能产生方向相反的瞬态磁场。因此，除了磁光效应，同一个磁光系数χ也决定着光磁效应，即圆偏振光诱导磁化。相比于“磁共振”，即通过电磁场的磁场分量使得微波光子与磁矩耦合，逆法拉第效应则是通过光的电场分量起到了类似的作用。上述公式的推导过程考虑了单色光激发，并且运用了热平衡近似。当[E（ω）×E（ω）∗]的改变速度比磁有序材料中的基本时间尺度，如自旋进动周期或自旋–晶格弛豫时间快时，就必须研究逆法拉第效应所产生的影响。

逆法拉第效应亦可从微观角度进行考虑。一个飞秒激光脉冲（∆t=100 fs）内的自旋激发过程，经傅立叶变换后，可以在频域上进行考虑，如图17（c）所示。起初，电子处于基态，自旋向上。如果基态是非简并的，那么自旋轨道耦合可以忽略。当光子作用到一个电子上，在电子跃迁期间，电子波函数的多个本征态将发生叠加，这必将有效地增加电子的轨道角动量，导致电子–轨道耦合，发生强烈的自旋翻转。当光子能量低于能隙，不能激发起真实的电子跃迁，但是会导致基态电子自旋的翻转（激发到一个虚态，退激发过程非常快）。这个过程伴随着光子的相干辐射，即ħω2=ħ（ω1−Ωm）。在磁有序材料中，ħΩm对应于一个磁振子的能量。如果频率ω1和ω2都在同一个激光脉冲内，那么激光诱导自旋翻转过程就是“相干”受激过程。自旋翻转时间（τsf）由受微扰的基态上的自旋–轨道相互作用能ESO给出。对于磁光系数大的材料，若自旋–轨道耦合能超过50 meV，那么自旋翻转过程可以快至τsf∼ħ/ESO∼20 fs。这一微观图像可以用来描述圆偏振光产生亚皮秒时间尺度上的有效磁场。

上述的自旋翻转过程是在“电偶极近似”下允许的，这一机制的效率高于“磁偶极跃迁”，且不需要光子的湮灭。能量从光子转移到自旋（磁振子）是通过非弹性散射过程。尽管一些光子失去了小部分能量，但光子总数仍然不变。值得注意的是，自旋翻转过程是受激Raman散射过程，受激发的和再次辐射的光子具有相同的极化，表明这样一个光诱导自旋翻转并不伴随光子角动量的损耗。然而这也受到了Woodford理论研究的挑战，他认为通过光子的线性角动量可以提供材料的自旋角动量[111]，当然这需要进一步实验的验证。此外，Yoshino的研究表明，基于经典的电子运动模型，逆法拉第效应可以与光学常数，即材料的复折射率指数的实部和虚部联系起来[112]。

图18.由于逆法拉第效应，圆偏振的飞秒光脉冲在DyFeO3中激发高频自旋进动，摘自文献[113]。

由于Dzyaloshinskii-Moriya相互作用，DyFeO3中两套铁离子的反铁磁耦合并非严格平行，产生约8 G的自发磁化（Ms）。尽管这一自发磁化强度非常小，由于极强的自旋–轨道耦合，DyFeO3表现出巨大的法拉第旋转角3000◦cm−1。2005年，Kimel等首次在倾角反磁体系DyFeO3中光激发百吉（亚太）赫兹的反铁磁共振模式[113]。如图18所示，在相反旋性的圆偏振光脉冲激发下（垂直于[001]晶轴方向），DyFeO3的法拉第旋转信号随时间的演化过程。在光激发后的60 ps内，清晰可辨三个不同的过程：（1）在零时间延迟点，观察到法拉第旋转角瞬间发生突变。圆偏振抽运光的“旋性”控制着光诱导磁化的方向；（2）在零延迟处的瞬态磁光信号之后，可观察到频率为0.2 THz（周期为5 ps）的磁振荡信号。磁振荡的相位由圆偏振光的“旋性”所决定，表明光子和自旋角动量的有效耦合；（3）除振荡外，还观察到一个时间常数约为100 ps的指数衰减过程。解释为光诱导磁化矢量的平衡方向发生改变，并衰减至初始状态。

除了反铁磁晶体，圆偏振飞秒激光脉冲在磁光晶体NaTb（WO4）2[114]，TGG[115]和磁流体[bmim]FeCl4[116]等中也可诱导瞬态磁化响应。旋向相反的圆偏振抽运光得到变化方向相反的旋转角信号和椭圆率信号。这是由于圆偏振光在磁光晶体和顺磁流体中产生的瞬态有效磁场的方向取决于抽运光的圆偏振旋向。NaTb（WO4）2和TGG晶体的顺磁特性决定了其几十飞秒的自旋弛豫时间，探测光旋转角信号和椭圆率信号的半高全宽均约为500 fs，其强度随着抽运光脉冲能量密度的增加呈线性增长，可用于实现全光磁开关。

2.THz脉冲激发自旋共振

铁磁共振一般指在外磁场作用下铁磁材料对电磁波的吸收，是外磁场作用下Zeeman能级劈裂的结果。对于常规铁磁材料，在不是很高的外磁场作用下（几个特斯拉磁场），其铁磁共振频率一般在射频和微波波段。对于反铁磁结构，由于内部很强的交换作用以及磁各向异性，大多数反铁磁材料的本征磁偶极跃迁频率在太赫兹波段。在Nel温度以下，NiO有两个铁磁共振模式，一个为1 THz的面外共振模式，另一个为0.14 THz的面内共振模式[117]。

反铁磁结构中基于磁偶极跃迁的铁磁共振与一般意义上的基于Zeeman效应的铁磁共振有所不同，前者是太赫兹波的磁场分量与反铁磁结构的本征模式共振而激发的磁偶极跃迁，是非平衡态下的磁化进动；后者是静态磁场作用下的稳态过程。宏观上，瞬态THz磁场（BTHz）的方向正交于材料的宏观磁化矢量M，必将产生一个作用于M的瞬态Zeeman转矩[118]：如图19（a）所示，这一瞬态转矩T使得反铁磁介质中的磁化矢量M偏离平衡位置。当瞬态磁场BTHz消失后，M将围绕材料的有效磁场以Larmor频率进动，并最终弛豫到平衡位置。磁化矢量M的进动过程中，旋转的磁偶极子会辐射圆偏振的电磁波，

此电磁波的频率等于磁化矢量的进动频率，这一过程称为自由感应衰减（FID）。

图19.(a)超短THz脉冲的磁场分量BTHz激发相干磁化振子，通过磁偶极跃迁相互作用，转矩作用于自旋M上诱导自旋进动；(b)在NiO中，THz激发周期约为1 ps的自旋波（自旋箭头的连线），摘自文献[118]。

对于频率范围0.1∼10 THz的太赫兹电磁波辐射，相应的能量范围在0.4∼40 meV。固体中许多决定材料基本性质的“元激发”的能量均在该能量范围内，如等离子体、声子、磁化振子、超导能隙和电子自旋共振能谱等。利用飞秒激光脉冲光整流和光电导天线方法可以产生0.1∼3 THz的THz辐射，其电场振幅达MV/cm，相应的磁场振幅达1 T量级（B=E/c）。Kampfrath等利用高强度THz脉冲的磁场分量与磁有序结构相互作用[119，120]，实现对磁介质中自旋极化元激发的激发和相干调控，如图20所示。

在RFeO3（R=Y，Nd，Dy等稀土元素）倾角反铁磁结构中，利用THz脉冲磁场共振地激发其准铁磁模式（quasi-ferromagnetic mode，以下称FM）和准反铁磁模式（quasi-antiferromagnetic mode，以下称AFM）。如图20（b）所示，利用THz时域光谱，对c切YFeO3单晶进行了系统研究，通过改变THz的偏振方向，可以有效地激发频率在0.3 THz的FM模式[121]。其中位于0.45 THz的较宽的吸收带来源于YFeO3晶体在THz波段的双折射效应。磁有序结构吸收THz波后使自旋磁化离开平衡态，当THz脉冲离开后，偏离平衡位置的自旋取向将以其本征模式频率进动弛豫回平衡位置，YFeO3中M的进动辐射出具有圆偏振特性的THz波。

上面提到，两种自旋模式的THz共振激发取决于THz的电磁场极化方向和宏观磁化方向M。利用这一特性，THz时域光谱可用以探测宏观磁化方向在外触发下的重取向过程。当改变样品所处的环境温度或者施加强磁场等，都能改变稀土离子和铁离子之间的交换相互作用，诱导M发生旋转。当M和THz偏振方向的夹角发生变化，就能从自由感应衰减信号的振幅和频率等的变化读取出自旋重取向信息。通过研究稀土离子在Fe的重取向中扮演的微妙而重要的角色，有望设计成功能不同的自旋开关[122−124]。

从色散关系的角度，THz电磁波电场分量与介质相互作用可以用介电常数ε（ω）来描述，而其磁场分量与介质作用则可用磁导率µ（ω）来描述[125]。THz在磁有序介质中的传输，其复折射率n（ω）和复波阻抗Z（ω）分别为和。需要同时测量THz波的透射T（ω）和反射光谱R（ω），并根据R=（Z−1）/（Z+1）和T= exp（−inωd），确定介质的色散关系n（ω）与Z（ω）。Nmec等提出了仅用THz相干脉冲的透射谱，可直接得到介质的色散关系[126]，这一方法适用于亚毫米到厘米量级厚度的样品。相干THz脉冲会在样品界面上发生二次反射。根据THz透射主脉冲T0与二次反射脉冲T1的时间间隔，只要样品厚度精确测定，利用公式，可确定其色散关系［126］：

这里，d是样品厚度，f=ω/2π为频率，c为真空中的光速。利用这一方法，Song等研究了PrFeO3晶体在0.2∼1.0 THz波段的色散关系。当入射THz的电场与晶体c轴平行时，只有AFM模式被激发，0.41 THz处折射率的突变是由于磁导率的色散所引起的[127]。

图20.THz自旋共振激发(a)THz脉冲的磁场随时间的变化，法拉第旋转角信号上周期为1 ps的振荡起源于反铁磁自旋进动，插图为法拉第旋转角和THz驱动电场的振幅谱，摘自文献[119]；(b)c切YFeO3单晶中THz透射谱，摘自文献[121]。

3.自旋相干控制

固体材料中量子相干态的控制是实现未来信息技术的关键。为了实现自旋电子学和量子计算等新一代技术，就需要固体材料中的元激发或者跃迁具有能为外场所调控的长的相干时间。长期以来，在核磁共振领域，兆赫兹和吉赫兹的交流脉冲磁场被用来实现自旋的相干控制。然而，固体中磁化子的退相时间极短，因此，高强度的超短磁脉冲是实现固体中磁激发相干控制的关键。

首先介绍通过光脉冲串实现自旋进动的超快“非热相干控制”。如图21（a）所示，零延迟时间时，一个右旋圆偏振抽运光（σ+）触发磁化进动。当再用一个左旋圆偏振光（σ−）在进动周期的整数倍时激发DyFeO3，会使磁化矢量进一步远离平衡位置，从而导致随后的进动振幅大约是单脉冲激发时的两倍，如图21（b）所示。若第二个抽运脉冲是在奇数个半进动周期时到达样品，则磁化矢量将重新回到最初的平衡位置，抑制了磁化进动，如图21（c）所示。实验结果表明飞秒脉冲可以用来直接相干地控制自旋进动。当第二个脉冲到来时，根据进动的相位，能量可以从光脉冲转移到磁系统（进动振幅增强）或者从磁激发系统转移到光脉冲（进动振幅消失）。考虑到正铁氧体和石榴石中的本征阻尼较低[129]，因此存在长寿命的磁振子。超短激光脉冲可以瞬时地将长周期的相干进动完全关断。这一能量回到光脉冲的过程也可以认为是磁化振子的相干激光冷却过程。

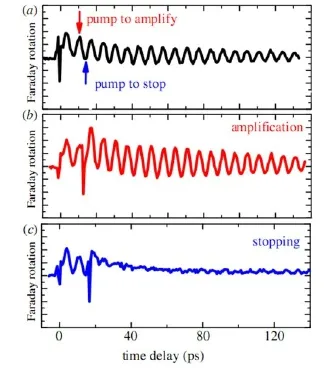
图21.两种圆偏振激光脉冲在DyFeO3中实现自旋的相干控制，摘自文献[128]。

THz脉冲中蕴藏的瞬态高强度磁场，是实现高频自旋波激发和控制的另一个潜在工具。反铁磁材料体系提供了实现THz自旋极化波的“非热”激发和相干控制的可能。Yamaguchi等利用THz脉冲对，研究了c−切和b−切的YFeO3晶体中FM和AFM模式的相干控制[130]。通过调节THz脉冲对的延迟时间，可以选者性地使某个自旋模式增强或消失。值得一提的是，作者发现基于THz磁场脉冲对实现自旋的相干控制不是源于自旋波的相干叠加，而是THz脉冲磁场直接与自旋波间的能量交换。Kampfrath等利用THz脉冲磁场激发NiO单晶中的自旋波，并利用一束同步的飞秒激光脉冲进行探测。基于同样的THz脉冲对，成功实现了NiO中AFM模式的激发和相干控制[120]。Jin等选择b切DyFeO3单晶为研究对象，FM模式的频率在0.38 THz，对应自旋极化波的周期TFM=2.6 ps，AFM模式的频率为0.52 THz，相应的振荡周期为TAFM=1.92 ps。图22（a）是利用双THz脉冲对FM模式的相干控制实验结果，当THz双脉冲的时间延迟T=1.5 TF时，可以看到辐射频率为0.38 THz的振荡完全消失，实现相干相消；当T=2.0 TF时，0.38 THz的自由感应衰减信号的振幅加倍；图22（b）是利用双THz脉冲对AFM模式的相干控制实验结果，当THz双脉冲的时间延迟T=1.5 TAF时，可以看到辐射的频率为0.52 THz的电磁波实现相干相消；而当T=2.0 TAF，辐射的频率为0.52 THz的电磁波振幅加倍，实现了相干相长。

图22.b切DyFeO3晶体的THz透射时域光谱，利用一定时间延迟的THz脉冲对实现对(a)FM和(b)AFM模式的相干相消和相干相长控制。

除了双脉冲相干控制，Jin等利用YFeO3晶体THz波段的双折射效应，提出用THz单脉实现反铁磁结构中自旋极化波的相干控制。如图23所示，其基本原理是入射到晶体中的THz脉冲由于双折射分解为o光和e光，通过调节入射THz偏振与晶体光轴的角度，可以得到任意强度比例的o光和e光，这两个偏振垂直的脉冲在晶体中传播伴随相应的相位延迟，从而实现对自旋极化的单THz脉冲相干控制[131]。

对于RFeO3（R=Y或Nd和Tm等稀土离子）倾角反铁磁结构，第一性原理计算结果表明如果R为4f电子不全空或全满稀土元素[132]，由于R与Fe离子间的相互作用，该结构的磁各向异性取向与温度有关，也就是说温度可诱导该结构的自旋重取向（如NdFeO3、ErFeO3等）：宏观磁化矢量M由高温下平行与c轴随着温度降低旋转90◦角度，至平行于晶体的a轴。如果R为非磁性金属，如Y、Pr等，不含有4f电子，则R与Fe之间作用可以忽略，则温度不可能诱导Fe离子的自旋重新取向，但外磁场却可以实现自旋取向相变。由于RFeO3共振吸收对THz磁场取向敏感，因而THz时域光谱为研究该类结构的自旋重取向等磁相变动力学特性提供了很好的研究手段。Yamaguchi等[133]利用THz时域光谱研究了ErFeO3单晶自旋重取向。对于c−cut的ErFeO3晶体，其自旋重取向温度区为97∼86 K，高温下晶体是Γ4相，垂直入射的THz波仅能激发其FM模式，低温下晶体是Γ2相，垂直入射的THz脉冲可以同时激发FM和AFM两个模式。同时，沿晶体c方向观测FID信号的偏振也不一样，FM的FID信号具有圆偏振特性，而AFM则表现为线偏振特性。

Jiang等[134]首次利用THz时域光谱对NdFeO3晶体的自旋重取向相变过程进行了研究。NdFeO3的自旋重取向温区较宽（170∼100 K），因而可以对其相变中的中间相（Γ4）进行研究，并研究了相变过程中AFM模式的幅度、共振频率和FID的偏振特性随相变温度的变化关系。

Constable等[123]结合中子衍射实验和THz光谱，讨论了NdFeO3晶体中自旋重取向的物理机制。实验结果与第一性原理计算结果相一致：自旋重取向源于温度相关的R-Fe作用和Fe-Fe作用的竞争结果。除了温度诱导自旋重取向外，外加磁场也可以诱导自旋重取向。Jiang等[135]基于全光纤THz时域光谱系统详细研究了外磁场诱导NdFeO3自旋重取向过程。其主要结论包括两点：（1）磁场诱导自旋重取向所需的临界磁场Hcr与温度有关，当温度接近自旋重取向温度时，临界磁场越小；（2）磁场诱导自旋重取向不可逆性：高温下（晶体处Γ4相）沿着晶轴a方向的外加磁场可以诱导自旋重取向发生；而低温下（晶体处于Γ2相），沿着晶轴c方向的外磁场则不能诱导自旋重取向。其内在原因与NdFeO3晶体的特殊磁各向异性结构有关，中子衍射的实验结果也应证了这一点。磁场诱导自旋重取向的不可逆性可以为设计磁存储和磁开关器件等自旋电子学器件提供重要参考。

图23.(a)当θ=0◦、45◦、90◦时，透过样品后THz波的电场强度，θ的定义如插图（下）所示。当θ=0◦时，振荡部分傅立叶变换谱的振幅(EFM)如插图（上）所示，(b)为振荡部分的放大，其时域区间为10～35 ps范围内的THz电场，实线是单指数衰减拟合，竖直的虚线旨在突显三个角度上THz自旋波的相位存在差异，摘自文献[131]。

图24.b−cut NdFeO3单晶中温度诱导自旋重取向相变的THz时域光谱研究。(a)表示NdFeO3的磁结构随温度变化示意图；(b)140 K温度下，自由感应衰减(FID)所辐射的电磁波电场强度随时间弛豫的三维轨迹图；(c)各种温度下FID信号在(ac)面上的投影。可以看到，250～170 K，晶体处于Γ4相，辐射的FID信号电场具有水平偏振，当温度低于100 K时，晶体处于Γ2相，FID信号电场具有垂直偏振，170～100 K温度区间，晶体处于Γ24相，辐射的FID信号电场在水平和垂直方向均有分量。摘自文献[134]。

对于非磁性金属，如YFeO3晶体，温度不能诱导其自旋重取向相变的发生。但是可以用外加磁场等方式触发其自旋重取向。Lin等[124]将THz时域光谱置于低温和强磁场系统下，研究了外磁场诱导YFeO3（c−cut）单晶的自旋重取向过程。无外加磁场时，从3 K到室温范围内，只有FM模式共振出现，且频率变化范围不大，表明从3∼300 K温区内，该晶体没有自旋重取向发生。但外磁场可以诱导YFeO3中自旋重取向的发生。下图给出250 K温度下，外磁场沿着晶体a轴施加，磁共振频率随外场变化情况。当外磁场强度低于2 T时，其FM模式的共振频率几乎不随磁场而变化，当磁场高于2 T时，FM模式的共振频率随外场增加而降低，出现模式软化，这是自旋重取向发生的征兆。进一步增加外磁场高于4 T时，FM模式的软化加剧，除了低频FM模式外，在0.55 THz处出现一个新的共振模式，这个模式与YFeO3的AFM模式频率接近。进一步研究表明，0.55 THz处的共振频率来自晶体的AFM模式共振。该模式频率几乎不随磁场增加而变化。通过朗道–栗弗席兹–吉尔伯特（LLG）方程并考虑YFeO3晶体自由能，可以数值得到FM和AFM模式频率随外磁场的关系，其趋势与实验结果相一致。

反铁磁和亚铁磁结构的磁共振频率一般在百GHz至THz频段，相干THz脉冲的磁场为研究这类磁有序的自旋极化的激发和相干控制提供了理想的实验方案。基于THz时域光谱，我们不但能获得磁共振的强度信息，而且还可以获得自旋极化的弛豫动力学，利用THz脉冲对可以选择性地激发和控制特定模式的自旋波。这对THz自旋电子学的研究开辟了新的研究领域和研究方法。THz波的磁场与磁介质自旋极化作用不但可以用于研究磁介质的自旋重取向相变动力学，而且当THz波所携带的磁场足够强时，还可以驱动磁有序介质中各种磁相变（如自旋重取向和磁化反转等相变）的发生[136，137]。这为研究磁相变的THz波非线性调控提供了研究新的研究思路。当然要实现THz波驱动的各种磁相变的发生所需要的THz脉冲磁场在数特斯拉甚至数十特斯拉量级，所以研究THz磁场近场增强效应，以实现几个量级的近场增强效应是实现磁振子的THz非线性调控一个有效思路。利用THz人工电磁材料实现电磁场的近场增强是目前一个比较现实的解决方案[13，139]。另外，THz光谱还可用于研究多铁材料的磁电耦合动力学。最后，值得一提的是，THz脉冲整形技术的发展，可以得到具有特定脉冲形状和相位的THz脉冲，也即可获得具有特定波形和相位分布的磁场分布，这为利用THz实现自旋波的有效相干控制提供了理想的研究思路和实现方法。

D.多铁性薄膜超快动力学

多铁材料（multiferroics）指的是同时具有铁电与铁磁两种以上有序参数的材料，且磁–电间存在一定的耦合，即能在外磁场作用下产生介电极化，在外电场作用下产生磁化[140]。1894年，居里预言磁电效应的存在，从此开启了磁电材料研究的大门。1960年，Astrove等在Cr2O3单晶中首次发现了多铁性[141]。尽管在后续的研究中陆续发现硼酸盐、稀土铁酸盐和磷酸盐等单相材料体系中，也存在磁电效应，然而所观察到的磁电耦合效应非常弱。因此，单相多铁性材料的研究进展缓慢，严重影响了多铁材料的发展。两个重大突破，重新掀起了世界范围内多铁材料研究的热潮。一是理论工作开始介入多铁性材料的研究，第一性原理计算旨在回答为什么磁性和铁电共存是如此的微弱，从而为多铁材料的研究提供了新方向；二是实验上成功地获得了两类不同的多铁材料。2003年，Ramesh等成功制备了具有良好铁电性和铁磁性的铁酸铋薄膜（BiFeO3，BFO），并发现薄膜形式BFO的多铁性能高于块材样品[142]。通过掺杂等手段，可以提高单相BFO多铁薄膜的铁电、铁磁和磁电耦合性能[143]。同一年，Tokura等发现了另一个新的多铁材料TbMnO3。这类材料的磁性和铁电性并非仅仅共存，而是磁性导致其铁电性[144]。此外，在钙钛矿结构的稀土锰氧化物（RMnO3）中，观察到不同外加磁场下，不同的介电行为，表明磁场对多铁材料介电特性的调控。与此同时，人们逐渐意识到了多铁材料潜在的应用价值，比如实现四种逻辑状态（上和下的极化，上和下的磁化），磁电传感器等。多铁材料的研究进入了高速发展阶段。

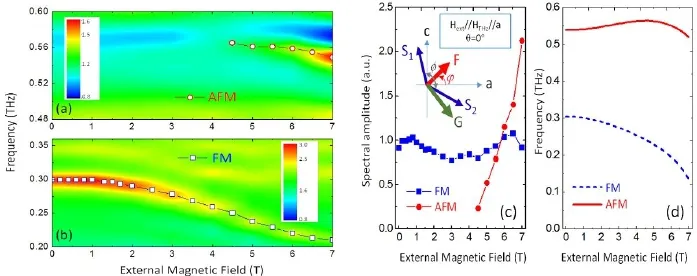
图25.外加磁场诱导c−切YFeO3晶体的自旋重取向THz时域光谱研究。YFeO3单晶中AFM(a)和FM(b)共振频率随外场变化关系，可以看到当H＞4 T时，FM共振频率出现剧烈软化，同时AFM共振开始出现。(c)FM（蓝）和AFM（红）吸收强度随外磁场变化，其中的插图表示了外磁场诱导晶体自旋重取向示意图；(d)基于LLG方程和磁自由能所计算的FM和AFM频率随外磁场的变化。摘自文献[124]。

为了理解多铁材料的基本现象，就必须了解支配这些特性的微观机制。多铁性的产生源自于材料体系中晶格、自旋、轨道以及电荷的强相互关联。理解电荷、自旋、轨道和晶格自由度间的耦合是多铁性材料体系的一个重要的研究课题。自旋–晶格之间的耦合机制还有待进一步完善。研究方案通常是通过外加磁场（电场）的变化研究电滞（磁滞）回线和温度依赖的磁化强度变化等。由于“相互作用”或者“耦合”常常伴随着能量转移，因此“光学方法”可以有效提供各种序参数间的耦合信息。实现不同外加条件（如电/磁场，温度和压强）下的原位“非接触”测量。抽运–探测光谱技术广泛地应用于材料的微观动力学研究，擅长在时域上同时探测多个自由度的演变过程以及各自由度之间的相互耦合。特别是温度依赖的抽运-探测光谱，被认为是研究多铁材料体系中，电子–声子和自旋–晶格相互作用的有效手段，为研究多铁氧化物磁电耦合的微观机制提供了不可或缺的动力学信息[145]。

1.电–声–磁相互作用

瞬态反射率变化（∆R/R）与介电常数∆ε的时间演化息息相关，在时域上直接反应电子–声子的能量交换过程。根据“三温度模型”，受激发的电子还会将能量传递给自旋系统。以La0.7Ca0.3MnO3为例，其电子、晶格和自旋的比热大小关系，Ce＜Cl，Ce＜Cs。当激光照射到样品表面，表面局域区域内的电子最先被激发（由于电子系统的比热最小），电子系统吸收光子能量，使得这一区域内电子温度高于附近的电子温度。电子–电子相互碰撞，使得局域电子的温度达到平衡，称为热化。热化过程的时间尺度在飞秒量级。热能通过电子–声子相互作用，从电子系统传递给晶格系统，使得电子和晶格的温度达到平衡，这段过程的时间尺度在亚皮秒–几个皮秒量级，称为“快过程”。Jin等系统研究了BFO薄膜的电子弛豫动力学过程，发现四方结构BFO薄膜中电子–晶格能量弛豫时间（τe−ph）要比六角结构BFO薄膜的τe−ph快，表明电子–声子相互作用对BFO薄膜的结构十分敏感。应力和对称性破缺使四方结构的BFO薄膜具有更大的电–声耦合强度[146]。

图26.通过拟合，得到两个激发光子能量下(a)慢过程的时间常数，(b)慢过程分量的幅度B和(c)准常数参量T∞随温度的变化关系。(a)、(c)垂直的虚线相应于转变温度Tc=120 K，摘自文献[148]。

此外，理论分析表明，多铁性样品中磁电耦合所对应的电磁振子元激发的能量一般在THz波段，所以，THz脉冲的电场可以激发多铁介质的磁振子，而THz脉冲磁场可以激发介质的电极化，从而有望实现THz频率的磁电互控。对于极强的THz辐射，强的磁脉冲与介质的相互用偏离谐振子模型，必须考虑磁偶极子相互作用的非线性效应，这种非线性作用对于自旋波的传输和控制提供了更为丰富的研究方法。

2.光致瞬态应变

除了通过载流子的弛豫过程研究BFO的瞬态光谱特性，越来越多的研究开始注重光诱导效应与铁电、铁磁和铁弹等特性的耦合。在开路电压下，BFO单晶的光生伏特效应与沿着电极化方向的晶体长度成正比[152]。Kundys等研究了光与BFO力学自由度的耦合，发现了BFO单晶波长依赖的尺寸变化，这一现象被称为光致应变效应[153]。尽管室温下BFO单晶中的光致应变效应已经开始得到学术界的重视，还需要进一步加深对光与铁弹动态耦合效应的理解。对于非中心对称材料，电磁场与物质相互作用的二阶非线性极化可以表示为[154]：

其中，χ(2)是二阶非线性极化率。E（t）和E∗（t）分别是光的电场分量及其共轭项。（30）式中等号右边的第一项为光诱导的直流极化项，反应光整流效应。这也是单晶块体材料中，光诱导产生THz的原因[155]；第二项与材料的二次谐波产生相关[156]。由于电致伸缩效应，二阶极化的直流项（t）会导致晶格畸变，从而产生纵向声学声子波[157，158]。当这一应力波传播通过样品，探测光脉冲在与行进的应力波相互作用后，频率将发生多普勒频移，类似于受激布里渊散射。因此，通过扫描抽运脉冲与探测脉冲间的时间延迟，可以获得纵向声学声子的传播行为。图26（a）描绘了光诱导纵向声学声子的传播与探测。

Chen等早期的研究已经发现，镧（La）和铌（Nb）共掺杂的BFO薄膜Bi0.8La0.2Fe0.99Nb0.01O3（BLFNO）相比于本征BFO薄膜，表现出更强的电极化特性[159]。因此，共掺杂的BLFNO薄膜的光致应变效应可能同样会得到加强。如图27（b）所示为室温下，（001）-STO衬底上的BLFNO薄膜和本征BFO薄膜的归一化瞬态反射率。通过快速傅立叶变换，可以观察到在36、33、25 GHz三处有峰，分别对应于（001）-Si、（001）-YSZ和（001）-STO衬底上的BLFNO薄膜。实验中，振荡频率不随激发光能量密度的变化而变化，其振幅正比于抽运光能量密度。这些振动被指认为纵向声学声子[160]。在[010]取向的斜方六角结构BFO单晶中也发现了频率为36 GHz的纵向声学模式。然而在薄膜样品中，我们并没有观察到在BFO单晶中所发现的频率为12.5和20 GHz的横向声学模式[157]。

图27.(a)抽运–探测技术研究光诱导应力波传播示意图。室温下，(001)-STO衬底上的(b)BLFNO薄膜和(c)本征BFO薄膜的归一化瞬态反射率。探测波长分别是(d)800 nm和(e)400 nm时，(001)-Si衬底上BLFNO薄膜的归一化瞬态反射率信号，摘自文献[160]。

通过设计复杂的氧化物异质结构，可以实现超快应力调制[162]。Sheu等利用时间分辨二次谐波光谱，全光探测和控制了超快时间尺度上电有序和磁有序的耦合。在Ba0.1Sr0.9TiO3（BSTO）/La0.7Ca0.3MnO3（LCMO）异质结中，抽运光激发了LCMO中的非平衡的准粒子，并与声子快速相互作用，发生在几十ps的自旋–晶格弛豫过程前。LCMO中自旋–自旋关联的减弱通过磁致伸缩效应会在BSTO上施加压力，从而通过压电效应调制了BSTO的铁电极化，这一过程的时间尺度远快于从LCMO到BSTO光诱导的热扩散。通过弹性耦合，实现了在铁磁/铁电异质结构中的一个超快的间接的磁电效应，这一过程比铁磁层中的自旋–晶格弛豫快[163]。

III.总结与展望

本文通过时间分辨的光谱技术，在飞秒时间尺度上给电子自旋动力学过程“拍照”。围绕着半导体块体及其纳米结构、铁磁、倾角反铁磁、多铁性磁电耦合材料等，综述了近年来光与电子自旋的相互作用。在什么“速度”和什么“空间尺度”上实现材料磁性状态的调制是目前磁性材料研究领域两个最前沿的课题。这些研究课题触及磁性材料中的各种基本极限，比如将目前磁存储器吉赫兹的开关速度极限向太赫兹频率推进；研制新型磁性微纳器件等。如何同时实现纳米尺度的空间分辨将是未来研究的方向之一[164−166]。

探测波长的选择范围可以从微波一直到X射线。X射线不仅可以实现钆铁钴合金薄膜中铁原子或钆原子特定的电子激发，且X射线的短波长可以用于实现纳米级的空间分辨率。分析时间分辨的X射线衍射图案可以得到每个化学元素的自旋角动量演化过程。

THz时域光谱技术对研究磁有序结构的自旋波的激发、弛豫、输运和相干控制具有其他自旋电子学研究方法所不具备的特点，如非接触性、宽带性和相干性等诸多优点，同时也是对常规自旋电子学研究方法的补充和拓展。利用THz光谱技术研究电子自旋特性才刚刚开始，随着研究的拓展和深入，我们相信THz光谱为自旋电子学的研究将会在磁化模式软化、THz脉冲磁场驱动磁相变和磁化反转和自旋–晶格耦合动力学中发挥更大的作用。利用强THz脉冲与磁有序介质非线性相互作用，实现磁振子的THz非线性调控是下一步THz自旋电子学所面临的挑战性研究课题。

除了自旋自由度的调控，人们开始展开全新的对轨道序的调制与应用。此外，利用飞秒激光所激发电子态间的相干，通过突然破坏强关联体系中各相之间的竞争与介电平衡从而实现磁有序转换，比如在Pr0.7Ca0.3MnO3中发现了飞秒时间尺度上光诱导的“反铁磁有序”向“铁磁有序”的转换过程[167]。

光与电子自旋相互作用的研究在不断向前发展，并逐渐开辟了太赫兹自旋电子学等新的研究方向。飞秒磁学这一领域的研究尚处于起步阶段，“超快退磁”背后的微观物理机制仍不明朗，需要大量的原创性实验和理论工作去丰富它。我们相信，飞秒磁学一定能推动凝聚态物理的新发展，最终开发出新型基于自旋的光电子学器件，造福人类。

致谢

上海大学超快光子学实验室开展光磁相互作用的研究已走过十年历程。在这个过程中得到许多老师和同学的指导和帮助，在此一并表示感谢：在半导体及其纳米结构中的自旋光注入和弛豫动力学研究中，受到中山大学赖天树教授和中科大吴明卫教授在实验和理论方面的帮助；基于光磁逆法拉第效应研究中，福州师范大学陈建中教授提供了高质量磁光晶体；利用THz脉冲研究自旋极化波的激发和相干控制，上海大学曹世勋教授提供了各种高质量的稀土铁氧化物单晶；澳大利亚University of Wollongong的程振祥教授提供了多种高质量多铁薄膜样品；天津大学太赫兹研究中心的韩家广和田振教授对强磁场下THz时域光谱的测试提供了很多帮助；感谢上海大学超快光子学课题组成员戴晔、阎晓娜、林贤、李栋、李高芳、周润泽、张郑兵、徐悦、薛新、张文涛、张泽宇和江俊杰等的出色工作。这项工作得到国家自然科学基金（10774099，11174195，11247290，11304186），高等学校博士点专项科研基金（20123018110003），上海市浦江人才计划（06PJ14042），上海科委科技攀登计划（09530501100），上海市教委创新重点项目（14ZZ101）和上海高校特聘教授（东方学者）岗位计划的资助。部分工作还受到山东师范大学优秀青年骨干教师国际合作培养计划的资助。

参考文献

[1]Gerlach W，Stern O.Zeitschrift fr Physik A Hadrons and Nuclei，1922，9(1)：353-355

[2]Uhlenbeck G E，Goudsmit S.Nature，1926，117：264-265

[4]Baibich M N，Broto J M，Fert A，Nguyen Van Dau F，Petroff F，Etienne P，Creuzet G，Friederich A，Chazelas J.Phys.Rev.Lett.，1988，61(21)：2472

[5]Moodera J S，Kinder L R，Wong T M，Meservey R.Phys.Rev.Lett.，1995，74(16)：3273

[6]Miyazaki T，Tezuka N，J.Magn.Magn.Mater.，1995，139(3)：L231-L234

[7]焦正宽，曹光旱.磁电子学.浙江：浙江大学出版社，2005

[8]翟宏如等.自旋电子学.北京：科学出版社，2013

[9]韩秀峰等.自旋电子学导论.北京：科学出版社，2014

[10]伯纯(Bertram H N)（作者），车晓东（注译），金庆原（注译）.磁记录理论.上海：复旦大学出版社，1981.1

[11]Kirilyuk A，Kimel A V，Rasing T.Rev.Mod.Phys.，2010，82(3)：2731

[12]Bigot J Y，Vomir M.Ann Phys.-Berlin，2013，525(1-2)：2-30

[13]Kirilyuk A，Kimel A V，Rasing T.Rep.Prog.Phys.，2013，76(2)：026501

[14]Beaurepaire E，Merle J C，Daunois A，Bigot J-Y. Phys.Rev.Lett.，1996，76(22)：4250

[15]Awschalom D D，Kikkawa J M.Phys.Today，1999，52：33-39

[18]曾谨言.量子力学.北京：科学出版社，2007.1

[19]Lai T，Liu X，Xu H，Jiao Z，Wen J，Lin W.Appl. phys.lett.，2006，88(19)：192106

[20]Seymour R J，Alfano R R.Appl.phys.lett.，1980，37(2)：231-233

[21]Tackeuchi A，Muto S，Inata T，Fujii T.Appl.phys. lett.，1990，56(22)：2213-2215

[22]Tackeuchi A，Wada O，Nishikawa Y.Appl.phys. lett.，1997，70(9)：1131-1133

[23]Tackeuchi A，Wada O，Mishikawa Y.Physica B，1999，272：318

[24]Hilton D J，Tang C L.Phys.Rev.Lett.，2002，89(14)：146601

[25]Lai T，Liu L，Shou Q，Lei L，Lin W.Appl.phys. lett.，2004，85(18)：4040-4042

[26]Lai T，Liu X，Xu H，Jiao Z，Lei L，Wen J，Lin W. Appl.phys.lett.，2005，87(26)：262110

[27]Lai T，Liu X，Xu H，Jiao Z，Wen J，Lin W.Appl. phys.lett.，2006，88(19)：192106

[28]Yu H L，Zhang X M，Wang P F，Ni HQ，Niu ZC，Lai T S.Appl.phys.lett.2009，94(20)：202109

[29]Kikkawa J M，Awschalom D D，Nature，1999，397：139-141

[30]Kikkawa J M，Awschalom D D.Phys.Rev.Lett.，1998，80(19)：4313

[31]Gupta J A，Knobel R，Samarth N，Awschalom D D，Science，2001，292(5526)：2458-2461

[32]刘晓东，半导体与铁磁薄膜中超快自旋动力学研究[D].中山大学博士学位论文(2008)

[33]He J，Zhong H，Phys.Rev.Lett..2010，105(4)：046601

[34]He J，Lo S S，Kim J，Scholes G D.Nano lett.，2008，8(11)：4007-4013

[35]Glinka Y D，Shahbazyan T V，Perakis I E，Tolk N H，Liu X，Sasaki Y，Furdyna J K.Appl.phys.lett.，2002，81(2)：220-222

[36]D’yakonov M I，Perel V I，Sov.Phys.JETP，1974，38：177

[37]Elliott R J.Phys.Rev.，1954，96(2)：266.

[38]Yafet Y.Sol.stat.phys.，1963，14：1-98

[39]Bir G L，Aronov A G，Pikus G E.Sov.Phys.JETP，1976，42：70

[40]Zerrouati K，Fabre F，Bacquet G，Bandet J，Frandon J，Lampel G，Paget D.Phys.Rev.B，1988，37(3)：1334

[41]Aronov A G，Pikus G E，Titkov A N.Sov.Phys. JETP，1983，57：680

[42]Clark A H，Burnham R D，Chadi D J，White R M. Phys.Rev.B，1975，12(12)：5758

[43]Kikkawa J M，Awschalom D D.Phys.Rev.Lett.，1998，80(19)：4313

[44]Paillard M，Marie X，Renucci P，Amand T，Jbeli A，Gerard J M.Phys.Rev.Lett.，2001，86(8)：1634-1637

[45]Kimel A V，Bentivegna F，Gridnev V N，Pavlov V V，Pisarev R V，Rasing T.Phys.Rev.B，2001，63(23)：235201

[46]Song P H，Kim K W.Phys.Rev.B，2002，66(3)：035207

[47]de Sousa R，Sarma S D.Phys.Rev.B，2003，67(3)：033301

[48]Dzhioev R I，Zakharchenya B P，Korenev V L，GammonD，Katzer D S.J.Exp.Theor.Phys.Lett.，2001，74(3)：182-185

[49]蒋建华，Ⅲ-Ⅴ族半导体及其纳米结构中的自旋动力学[D].中国科技大学博士学位论文(2010)

[50]Ma H，Jin Z M，Ma G H，Liu W M，Tang S H. Appl.Phys.Lett.，2009，94(24)：241112

[51]Ma H，Jin Z M，Wang L H，Ma G H.J.Appl.Phys.， 2011，109(2)：023105

[52]赵建华，邓加军，郑厚植.物理学进展，2007，27：109-150

[53]Crooker S A，Awschalom D D，Baumberg J J，Flack F，Samarth N.Phys.Rev.B，1997，56(12)：7574

[55]Li B，Tamargo M C，Meriles C A.Appl.Phys.Lett.，2007，91(22)：222114-3

[56]Ohno Y，Terauchi R，Adachi T，Matsukura F，Ohno H.Phys.Rev.Lett.，1999，83(20)：4196

[57]Sogawa T，Ando H，Ando S，Kanbe H，Phys.Rev. B，1998，58(23)：15652

[58]Liu W K，Whitaker K M，Smith A L，Kittilstved K R，Robinson B H，Gamelin D R.Phys.Rev.Lett.，2007，98(18)：186804

[59]Ruan X Z，Luo H H，Ji Y，Xu Z Y.Phys.Rev.B，2008，77(19)：193307

[60]Zhang Z，Jin Z，Ma H，Xu Y，Lin X，Ma G，Sun X. Physica E，2014，56：85-89

[61]Feng D H，Shan L F，Jia T Q，Pan X Q，Tong H F，Deng L，Sun Z R，Xu Z Z.Appl.Phys.Lett.，2013，102(6)：062408

[62]Feng D H，Li X，Jia T Q，Pan X Q，Sun Z R，Xu Z Z.Appl.Phys.Lett.，2012，100(12)：122406-4

[63]Ma H，Jin Z，Zhang Z，Li G，Ma G.J.Phys.Chem. A，2012，116(9)：2018-2023

[64]Ma H，Jin Z，Zhang Z，Ma G，Wang L.AIP Advances，2012，2(1)：012116

[65]Ma H，Jin Z，Zhang Z，Ma G，Wang L.AIP Advances，2012，2(1)：012116

[66]Giovanni D，Ma H，Chua J，Grtzel M，Ramesh R，Mhaisalkar S，Mathews N，Sum T.Nano lett.，2015

[67]夏建白，葛惟昆，常凯.半导体自旋电子学.北京：科学出版社，2008

[68]迪阿科诺夫主编，姬扬译.半导体中的自旋物理学.北京：科学出版社，2010

[69]Aeschlimann M，Bauer M，Pawlik S，Weber W，Burgermeister R，Oberli D，Siegmann H C.Phys. Rev.Lett.，1997，79(25)：5158

[70]Zhu H J，Ramsteiner M，Kostial H，Wassermeier M，Schnherr H-P，Ploog K H.Phys.Rev.Lett.，2001，87(1)：016601

[71]Lisowski M，Loukakos P A，Melnikov A，Radu I，Ungureanu L，Wolf M，Bovensiepen U.Phys.Rev. Lett.，2005，95(13)：137402

[72]Koopmans B，Malinowski G，Longa F D，Steiauf D，Fhnle M，Roth T，Cinchetti M，Aeschlimann M.Nat.mater.，2010，9(3)：259-265

[73]Eschenlohr A，Battiato M，Maldonado P，Pontius N，Kachel T，Holldack K，Mitzner R，Fhlisch A，Oppeneer P M，Stamm C.Nat.mater.，2013，12(4)：332-336

[74]Bigot J Y，Vomir M，Beaurepaire E.Nature Phys.，2009，5(7)：515-520

[76]Bonn M，Denzler D N，Funk S，Wolf M，Wellershoff S-S，Hohlfeld J.Phys.Rev.B，2000，61(2)：1101

[77]Kise T，Ogasawara T，Ashida M，Tomioka Y，Toku-ra Y，Kuwata-Gonokami M.Phys.Rev.Lett.，2000，85(9)：1986

[78]Zhang Q，Nurmikko A V，Miao G X，Xiao G，Gupta A.Phys.Rev.B，2006，74(6)：064414

[81]Koopmans B，Kicken H H J E，van Kampen M，de Jonge W J M.J.Magn.Magn.Mater.，2005，286：271-275

[82]Koopmans B，Ruigrok J J M，Longa F D，de Jonge W J M.Phys.Rev.Lett.，2005，95(26)：267207

[83]Malinowski G，Longa F D，Rietjens J H H，Paluskar P V，Huijink R，Swagten H J M，Koopmans B.Nat. Phys.，2008，4(11)：855-858

[84]Carva K.Nat.Phys.，2014，10(8)：552-553

[85]Schellekens A J，Kuiper K C，de Wit R R J C，Koopmans B.Nat.Commun，2014，5：4333

[86]Choi G M，Min B C，Lee K J，Cahill D G.Nat. Commun，2014，5：4334

[87]Urban R，Woltersdorf G，Heinrich B.Phys.Rev. Lett.，2001，87(21)：217204

[88]Koopmans B，Ruigrok J J M，Longa F D，de Jonge W J M.Phys.Rev.Lett.，2005，95(26)：267207

[89]He P，Ma X，Zhang J W，et al.Phys.Rev.Lett.，2013，110(7)：077203

[90]King J A，Ganguly A，Burn D M，et al.Appl.Phys. Lett.，2014，104(24)：242410

[91]Zhao H B，Talbayev D，Ma X，et al.Phys.Rev. Lett.，2011，107(20)：207205

[92]Zhao H B，Smith K J，Fan Y，et al.Phys.Rev. Lett.，2008，100(11)：117208

[93]Gong Y，Zhang Z，Ascienzo D，et al.EPLEurophys.Lett.，2014，108(1)：17010

[94]Bigot J Y.Physics，2012，5：11

[95]Radu I，Vahaplar K，Stamm C，et al.Nature，2011，472(7342)：205-208

[97]Bergeard N，L´opez-Flores V，HaltV，Hehn M，S-tamm C，Pontius N，Beaurepaire E，Boeglin C.Nat. Commun.，2014，5：3466

[98]Stanciu C D，Hansteen F，Kimel AV，Kirilyuk A，Tsukamoto A，Itoh A，Rasing T.Phys.Rev.Lett.，2007，99(4)：047601

[99]Vahaplar K，Kalashnikova A M，Kimel A V，et al. Phys.Rev.Lett.，2009，103(11)：117201

[100]Ostler T A，Barker J，Evans R F L，et al.Nat. Commun.，2012，3：666

[101]Evans R F L，Ostler T A，Chantrell R W，Radu I，Rasing T.Appl.Phys.Lett.，2014，104(8)：082410

[102]Satoh T，Terui Y，Moriya R，Ivanov B A，Ando K，Saitoh E，Shimura T，Kuroda K.Nat.Photonics，2012，6(10)：662-666

[103]（德）史拓，（德）希格曼著，姬扬译.磁学—从基础知识到纳米尺度超快动力学.北京：高等教育出版社，2012

[104]Beaurepaire E，Turner G M，Harrel S M，Beard M C，Bigot J-Y，Schmuttenmaer C A.Appl.Phys. Lett.，2004，84(18)：3465-3467

[105]Hilton D J，Averitt R D，Meserole C A，Fisher G L，Funk D J，Thompson J D，Taylor A J，Opt.Lett.，2004，29(15)：1805-1807

[106]Shen J，Fan X，Chen Z，DeCamp M F，Zhang H，Xiao J Q，Appl.Phys.Lett.，2012，101(7)：072401

[107]Kampfrath T，Battiato M，Maldonado P，et al.Nat. Nanotechnol.，2013，8(4)：256-260

[108]Averitt R D，Nat.Nanotechnol.，2013，8(4)：232-233

[109]Rungsawang R，Perez F，Oustinov D，et al.Phys. Rev.Lett.，2013，110(17)：177203

[110]Van der Ziel J P，Pershan P S，Malmstrom L D. Phys.Rev.Lett.，1965，15(5)：190

[111]Woodford S R.Phys.Rev.B.，2009，79(21)：212412

[112]Yoshino T.J.Magn.Magn.Mater.，2011，323(20)：2531-2532

[113]Kimel A V，Kirilyuk A，Usachev P A，et al.Nature，2005，435(7042)：655-657

[114]Jin Z，Ma H，Wang L，Ma G，Guo F，Chen J.Appl. Phys.Lett.，2010，96(20)：201108-3

[115]金钻明，郭飞云，马红，王立华，马国宏，陈建中.物理学报.2011，60：087803

[116]Jin Z，Ma H，Li D，Ma G，Wang M，Zhao C.J. Appl.Phys.，2011，109(7)：073109

[117]Satoh T，Cho S J，Iida R，et al.Phys.Rev.Lett.，2010，105(7)：077402

[118]Kono J.Nat.Photonics，2011，5(1)：5-6

[119]Kampfrath T，Sell A，Klatt G，et al.Nat.Photonics，2011，5(1)：31-34

[120]Kampfrath T，Tanaka K，Nelson K A.Nat.Photonics，2013，7(9)：680-690

[121]Zhou R，Jin Z，Li G，Ma G，Cheng Z，Wang X. Appl.Phys.Lett.，2012，100(6)：061102

[122]Yamaguchi K，Kurihara T，Minami Y，Nakajima M，Suemoto T.Phys.Rev.Lett.，2013，110(13)：137204

[123]Constable E，Cortie D L，Horvat J，et al.Phys. Rev.B，2014，90(5)：054413

[124]Lin X，Jiang J，Jin Z，Wang D，Tian Z，Han J，Cheng Z，Ma G.Appl.Phys.Lett.，2015，106(9)：092403

[125]刘公强，乐志强.沈德芳磁光学上海：上海科学技术出版社.20011

[127]Song G，Jiang J，Wang X，Jin Z，Lin X，Ma G，Cao S.J.Appl.Phys.，2013，114(24)：243104

[128]Kimel A V，Kirilyuk A，Rasing T.Laser&Photonics Reviews，2007，1(3)：275-287

[129]Hansteen F，Kimel A，Kirilyuk A，Rasing T.Phys. Rev.Lett.，2005，95(4)：047402

[130]Yamaguchi K，Nakajima M，Suemoto T.Phys.Rev. Lett.，2010，105(23)：237201

[131]Jin Z，Mics Z，Ma G，Cheng Z，Bonn M，Turchinovich D.Phys.Rev.B，2013，87(9)：094422

[132]Chen L，Chen T，Li T，et al.J.Appl.Phys.，2012，111(10)：103905

[133]Yamaguchi K，Kurihara T，Minami Y，Nakajima M，Suemoto T.Phys.Rev.Lett.，2013，110(13)：137204

[134]Jiang J，Jin Z，Song G，Lin X，Ma G，Cao S，Appl. Phys.Lett.，2013，103(06)：062403

[135]Jiang J，Song G，Wang D，Jin Z，et al.Magneticfield induced irreversible spin switching in NdFeO3: A terahertz study，未发表数据

[136]Wienholddt S，HinzkeD，Nowak U.Phys.Rev.Lett.，2012，108(24)：247207

[137]Shalaby M，Vidal F，Peccianti M，et al.Phys.Rev. B，2013，88(14)：140301(R)

[138]Kurihara T，Nakamura K，Yamaguchi K，et al.Phys. Rev.B，2014，90(14)：144408

[139]Mukai Y，HiroriH，Yamamoto T，Kageyama H，Tanaka K.Appl.Phys.Lett.，2014，105(02)：022410

[140]何泓材，林元华.南策文科学通报.2008，53：1136

[141]Astrov D N.Soviet Physics Jetp-Ussr，1960，11(3)：708-709

[142]Wang J，Neaton J B，Zheng H，et al.Science，2003，299(5613)：1719-1722

[143]Cheng Z X，Li A H，Wang X L，et al.J.Appl. Phys.，2008，103(7)：07E507-3

[144]Kimura T，Goto T，Shintani H，Ishizaka K，Arima T，Tokura Y.Nature，2003，426(6962)：55-58

[145]Basov D N，Averitt R D，Van Der Marel D，Dressel M，Haule K.Rev.Mod.Phys.，2011，83(2)：471

[146]Jin Z，Xu Y，Zhang Z，Li G，Lin X，Ma G，Cheng Z，Wang X，Appl.Phys.Lett.，2012，100(7)：071105

[147]Lobad A I，Averitt R D，Kwon C，Taylor A J.Appl. Phys.Lett.，2000，77(24)：4025-4027

[148]Jin Z，Ma H，Li G，Xu Y，Ma G，Cheng Z，Appl. Phys.Lett.，2012，100(2)：021106

[149]Talbayev D，Trugman S A，Balatsky A V，Kimura T，Taylor A J，Averitt R D.Phys.Rev.Lett.，2008，101(9)：097603

[150]Wall S，Prabhakaran D，Boothroyd A T，Cavalleri A.Phys.Rev.Lett.，2009，103(9)：097402

[151]Qi J，Yan L，Zhou H D，Zhu J-X，Trugman S A， Taylor A J，Jia Q X，Prasankumar R P.Appl.Phys. Lett.，2012，101(12)：122904

[152]Kundys B，Viret M，Colson D，Kundys D O.Nat. mater.，2010，9(10)：803-805

[153]Kundys B，Viret M，Meny C，Costa V Da，Colson D，Doudin B.et al.Phys.Rev.B，2012，85(9)：092301

[154]Shen Y R.Principles of nonlinear optics Now York：Wiley，1984.1

[155]Talbayev D，Lee S，Cheong S W，Taylor A J.Appl. Phys.Lett.，2008，93(21)：212906

[156]Yokota H，Haumont R，Kiat J M，Matsuura H，Uesu Y，Appl.Phys.Lett.，2009，95(8)：082904

[157]Ruello P，Pezeril T，Avanesyan S，VaudelG，GusevV，InfanteI C，Dkhil B，Appl.Phys.Lett.，2012，100(21)：212906

[158]Chen L Y，Yang J C，Luo C W，et al.Appl.Phys. Lett.，2012，101(4)：041902

[159]Cheng Z，Wang X，Dou S，Kimura H，Ozawa D. Phys.Rev.B，2008，77(9)：092101

[160]Jin Z，Xu Y，Zhang Z，Lin X，Ma G，Cheng Z，Wang X.Appl.Phys.Lett.，2012，101(24)：242902

[161]Thomsen C，Grahn H T，Maris H J，Tauc J.Phys. Rev.B，1986，34(6)：4129

[162]La-o-vorakiat C，Tian Y，Wu T，Panagopoulos C，Zhu J-X，Su H，Chia Elbert E M，Appl.Phys.Lett.，2014，104(14)：141602

[163]Sheu Y M，Trugman S A，Yan L，Jia Q X，Taylor A J，Prasankumar R P.Nat.commun.，2014，5：5832

[164]Graves C E，Reid A H，Wang T，et al.Nat.mater.，2013，12(4)：293-298

[165]Hashimoto Y，Khorsand A R，Savoini M，et al.Rev. Sci.Instrum.，2014，85：063702

[166]Guyader L L，Savoini M，Moussaoui S E，et al.Nat. Commun.，2015，6：5839

[167]Li T，Patz A，Mouchliadis L，Yan J，Lograsso T A，Perakis I E，Wang J，Nature，2013，496(7443)：69-73

Recently，the development of ultrashort pulse laser technology provides an effective tool for investigating the interaction of light and matter on critical timescales.The studies on spin dynamics have become a new forefront of condensed matter physics.In this review，we attempt to analyze the rich physics of dynamical electron spins pumped and probed by time-domain optical measurements focusing on common attributes revealed by diverse materials.The spin injection and relaxation are the central problems of spintronics in semiconductors.We discuss the mechanism of ultrafast demagnetization and spin procession in magnetically ordered structures.Our interests also include the opto-magnetic effect，spin wave excitation and coherent control with THz magnetic field.Finally，important information on charge-lattice and spin-lattice coupling can be provided by ultrafast spectroscopy.

Opto-magnetic interaction and ultrafast optical manipulation of spin waves

Jin Zuan-Ming1，Ma Hong2，Ma Guo-Hong1
1.Department of Physics，Shanghai University，Shanghai，200444，China 2.College of Physics and Electronics，Shandong Normal University，Shandong，250014，China

spintronics；ultrafast spectroscopy；terahertz；semiconductor nanostructures；ferromagnetic films；multiferroic，ultrafast demanetization；inverse Faraday effect；coherent control；spin current

date：2015-03-12

O43

10.13725/j.cnki.pip.2015.05.003

*ghma@staff.shu.edu.cn

1000-0542（2015）05-212-28212

光磁相互作用及自旋极化的光学调控

目录

I.引言

II.基本概念及研究进展

III.总结与展望

致谢