一种新的TOFD检测平板对接焊缝缺陷深度的计算方法

伍卫平，范钦红

(1.水利部水工金属结构质量检验测试中心， 郑州 450044;2.郑州辰维科技股份有限公司， 郑州450001)



一种新的TOFD检测平板对接焊缝缺陷深度的计算方法

伍卫平1，范钦红2

(1.水利部水工金属结构质量检验测试中心， 郑州 450044;2.郑州辰维科技股份有限公司， 郑州450001)

针对TOFD检测应用最为广泛的平板对接焊缝，在常规TOFD检测中焊缝缺陷深度计算的基础上，进行了进一步的数学推导，得到了一种更简洁的基于时差的数学表达式，以用于缺陷深度的测量计算。该方法无需进行声速和探头入射点间距值的测量，只需利用TOFD检测设备读取有关的时间参数及人工输入板厚值就可进行计算，避免了声速、探头入射点间距值的输入精度导致的测量误差。并通过扫查TOFD对比试块，测量其中的横孔缺陷的深度，验证了该方法的计算精度和可行性，取得了满意的效果。最后,对于存在余高的平板对接焊缝，提出了为提高计算精度而进行板厚值修正的方法。

超声衍射时差法;平板对接焊缝;时差计算;缺陷深度;深度误差;板厚修正

超声衍射时差法(Time of flight of diffraction，TOFD)[1]是一种依靠从缺陷的端角和端点处得到衍射信号来检测焊缝中缺陷的方法，其以直通波和底面反射波为参考基准波，根据缺陷端部产生的衍射信号的时差参数，通过一定的几何三角关系的计算，对缺陷进行定位和定量，检测原理如图1所示。TOFD技术具有检测速度快、定量精度高、定位准确和检测结果直观等优点。平板对接焊缝和管道环向对接焊缝为主的规则几何形状构件的焊接接头检测是其主要的应用领域之一。

图1　TOFD检测原理示意

TOFD做非平行扫查时，是假定缺陷位于焊缝中心线上的，也即在探头对连线的中心位置，则缺陷深度h为：

(1)

式中：CL为纵波的传播速度;t为超声波在工件及楔块对中传播的总时间;t0为超声波在单个楔块探头楔块中传播的时间;s为探头入射点间距的1/2。

若以直通波为参考起点进行直通波校准，根据直通波及缺陷衍射波声程差，有：

(2)

则根据式(2)可得到缺陷深度h：

(3)

式中：Δt为缺陷上端点的衍射波与直通波间的传播时间差。

同理可计算出缺陷下端点的深度，从而得到缺陷的高度。

目前市场上的主流TOFD设备工作时一般根据公式(1)或(3)来计算缺陷的深度，其中需要用到的时间值或时差值是通过设备读取的；而纵波声速CL、探头入射点间距2s值、楔块对的延时2t0是通过测量后人工输入设备的(设备在利用式(3)进行计算时，无需测量和输入的楔块对延时2t0)，这几个参数的精度直接影响着缺陷深度的测量误差。

常规的TOFD检测中，为了减少测量误差，需要进行有关的校准：在利用式(1)进行计算时，要进行声速CL和楔块对延时2t0的校准，则必须在A扫描信号中找准直通波和底面反射波的位置，输入底面反射波所对应的准确的板厚值及探头入射点间距值；在利用式(3)进行计算时，要进行楔块对延时2t0的校准，则必须在A扫描信号中找准直通波的位置，输入准确的探头入射点间距值。

1　TOFD检测中常规时差计算方法的缺陷深度误差分析[2]

由式(1)和(3)可看出，人工输入设备中的纵波声速CL、探头入射点间距2s值及楔块对延时2t0的精度直接影响着缺陷深度的计算。对于时间参数，目前的TOFD设备数字化采样频率很高，一般可达到50 MHz以上，因此时间参数的测量精度可达到0.02 μs以上，时间参数测量精度引起的计算误差很小，故只讨论CL和s值对深度测量的影响。

根据未进行直通波校准的式(1)，求h关于s的偏导数，得到：

(4)

根据进行过直通波校准的式(3)，求h关于s的偏导数，得到:

(5)

由式(4)和(5)可以发现，测量误差δh受s值、人工输入的探头入射点间距所导致的偏差δs和缺陷真实深度h值的影响；人工输入的纵波声速CL不影响测量误差δh。

根据未进行直通波校准的式(1)，求h关于CL的偏导数，得到：

(6)

根据进行过直通波校准的式(3)，求h关于CL的偏导数，得到:

(7)

由式(6)和(7)可以发现，测量误差δh受s值、人工输入的探头入射点间距所导致的偏差δs、缺陷真实深度h值、人工输入的纵波声速CL的影响。

2　一种新的基于时差的缺陷深度计算方法

为了减少因人工输入设备中的纵波声速CL、探头入射点间距2s值、楔块对延时2t0这三个参数的精度对缺陷深度的测量误差，并且减少有关校准声速和楔块延时的步骤，简化检测程序，笔者提出了一种新的计算方法。

直通波、底面反射波、底面变形波在工件中传输的时间tL、tbw、tcw(已经减去了超声波在楔块对中传播的时间2t0)可用下式表示：

(8)

式中：CL、CS分别为纵波、横波在工件中的传播速度;T为底面发射波所对应的厚度(一般为工件板厚值)。

将CL、CS、s看作未知数，求解式(8)中的方程组，得到：

(9)

缺陷衍射纵波信号在工件中传输的时间用tx表示(已经减去了超声波在楔块对中传播的时间2t0)，缺陷深度计算值用hx表示；将式(9)代入式(1)，则推导出笔者提出的缺陷深度计算公式：

(10)

式(10)为笔者通过数学推导得到的一种新的基于时差的缺陷深度的计算方法，通过该式只需要根据相关的时间参数和工件板厚值T(准确地说应是底面发射波对应的厚度)来计算缺陷深度，而无需进行直通波或者底波的校准，简化了操作步骤，且无需输入CL和s值，避免了纵波声速CL和s值引起的误差。

3　试验验证

试验采用的TOFD设备为以色列的ISONICStar，楔块角度为60°，探头中心频率为5MHz、晶片尺寸为φ6mm。采用厚度为50mm的TOFD试块，表面开有一条长40mm、深2mm、宽0.2mm的矩形槽；在另一侧离开槽表面深度分别为12.5,37.5,46mm处(圆心处的深度)，有直径分别为φ3、φ2.5、φ2mm，长度分别为60,45,30mm的平行于表面的三个侧孔，即三个孔上端点深度分别为11, 36.25, 45mm。试块尺寸示意见图2。

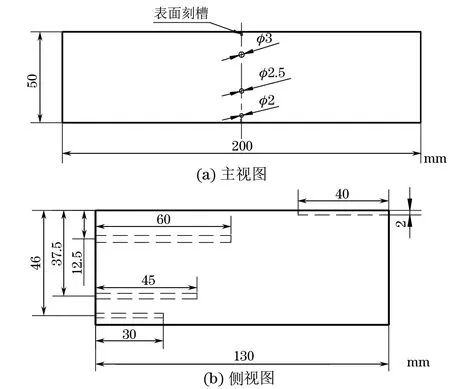
图2　TOFD试块尺寸示意

以开槽表面为扫查面，分别进行探头入射点间距为57,115,144 mm的对中非平行扫查(扫查图谱见图3)。考虑到上表面的检测盲区比较大，尤其是在探头入射点间距值比较大时；而最浅的孔埋深只有11 mm，其衍射信号容易与直通波混合在一起，深度测量误差比较大，因此试验部分只用所提出的新方法来测量实际深度为36.25,45 mm的两个孔的深度值。

在扫查该对比试块前，测量楔块对的延时为4.74 μs，试块中纵波声速为5 930 m·s-1。试验时时间参数测量位置选在对应脉冲信号的0.5个周期处(即D扫描灰度图中对应位置第一个黑-白分界线处)。

三种不同的探头入射点间距值的扫查，直通波在试块中传输时间tL分别为10.27,19.97,24.71 μs，则可以计算出理论探头入射点间距值分别为60.9,118.4,146.5 mm，与人工输入设备中的57,115,144 mm的差值分别为3.9,3.4,2.5 mm。按照常规的时差计算方法，缺陷深度计算误差较大，尤其是在未进行直通波校准时更大。

对于探头入射点间距值存在误差的情况，若δs=1 mm(即探头入射点间距值的偏差为2 mm)，采用常规的缺陷深度计算方法，根据式(4)与(5)，得到深度误差δh随真实深度变化的曲线如图4。

由图4可以发现，进行直通波校准后，深度测量精度得到了较大的提高；随着探头入射点间距值的增大，测量误差变小；随着缺陷深度的增大，测量误差增大。该情况下声速对测量精度没有影响。

对于输入设备中的声速CL存在误差的情况，如声速存在1%的偏差(即δCL=1%CL)，采用常规的缺陷深度计算方法，根据式(6),(7)，得到深度误差δh随真实深度变化的曲线见图5。

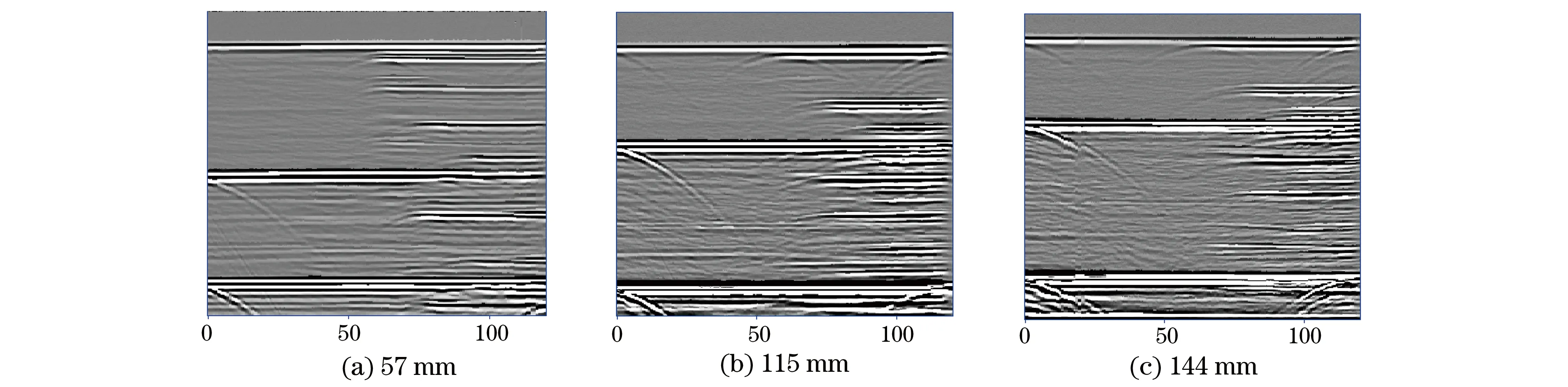
图3　不同探头入射点间距时的非平行扫查图谱

图4　不同探头入射点间距时的深度误差曲线(间距误差δs=1 mm，CL=5 930 m·s-1)

图5　不同探头入射点间距时的深度误差曲线(声速误差为1%，CL=5 930 m·s-1)

由图5和式(7)可以发现，进行直通波校准后，深度测量精度得到了较大的提高；随着探头入射点间距值的增大，测量误差变小；随着缺陷深度的增大，测量误差增大；随着声速的增大，测量误差变小。

按照笔者所提出的新计算方法，用tx表示缺陷衍射信号在工件中传输的时间，hx表示深度计算值，dx表示深度真值。表1为有关的深度计算结果，图6为对应的缺陷深度计算曲线。

分析表1中的数据，可以发现孔的深度测量精度很高；将表1中的数据与常规时差计算方法所对应的误差曲线(图4,5)进行对比，可以看出笔者提出的计算方法的精度明显高于常规计算方法，其很好地避免了声速、探头入射点间距值的偏差导致的误差。故文章所提方法的误差主要来自参数T。

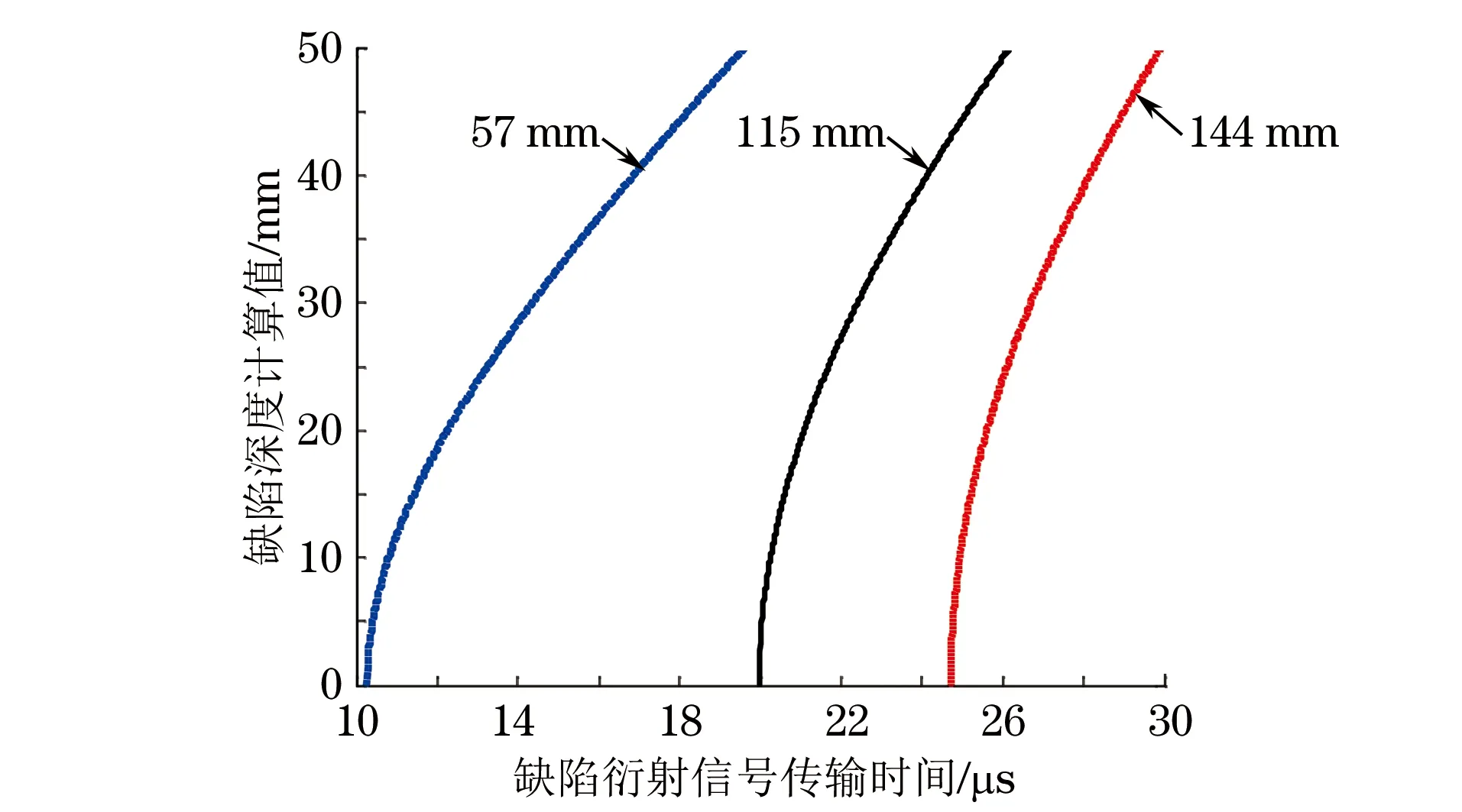
图6　新的时差计算法对应的缺陷深度计算曲线

4　带余高的平板对接焊缝中工件板厚的修正

根据式(10)可以看出，底面反射波所对应的工件板厚值T直接影响计算精度，因此对于有焊缝余高的平板对接焊缝，找准底面反射波所对应的真正板厚T′尤为重要。

表1　不同探头入射点间距时缺陷深度的计算值

对于有余高的焊缝，在TOFD扫查所对应的D扫描灰度图中，其底波是图7中焊趾部位的衍射信号；焊趾相当于一个轴偏离缺陷，其声程等于经过底面焊趾的椭圆曲线e1的长轴2a，该声程与焊缝底部中心深度为T′处的点的衍射信号声程一致：

(11)

输入设备中的板厚值不再是板厚T，而是图7中所示的T′(T′>T)，其等于椭圆曲线e1所对应的短半轴长b[3-4]：

(12)

焊缝余高d0一般只有几个毫米，远远小于探头入射点间距值，因此对于大多数情况，以下不等式是成立的：

(13)

因此，为了提高计算精度，需要对底面反射波所对应的板厚进行修正，不能简单地用T代替T′。

板厚修正值ΔT可以表示为：

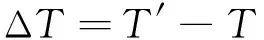
(14)

图7　带余高的平板对接焊缝TOFD检测示意

图8　带余高的平板对接焊缝板厚修正曲线

图8为针对不同探头入射点间距值和不同焊缝宽度2b0情况下的板厚修正曲线。通过图7所示的几何关系和图8中的曲线分析可以看出：探头入射点间距值越大、底部焊缝宽度2b0越小，则板厚修正值越小，T′越接近T，因此深度误差越小。

在焊缝余高里位于深度区间T′～T+d0的缺陷是TOFD检测的盲区，会出现漏检的情况[5]。焊缝余高的存在增加了底部焊缝中心的盲区，但可减少焊缝底部熔合线附近的轴偏离底面盲区[6]的情况。

5　结语

针对TOFD检测应用最为广泛的平板对接焊缝，根据TOFD检测时差计算的基本原理而提出的新的缺陷深度计算方法，只需要人工输入唯一的一个表示底面反射回波信号所对应的板厚值参数，而无须输入声波速度、探头入射点间距参数，避免了这两个参数对缺陷计算精度的影响，也无需进行直通波校准等操作，省略了CL,s和2t0的校准，优化了检测时的设备设置和操作步骤，提高了缺陷深度的测量精度；并且,对于带焊缝余高的情况，提出了为提高计算精度而进行板厚修正的方法。所提出的新的计算方法在实际检测工作中具有较大的参考价值和指导意义。

[1]胡先龙，季昌国，刘建屏，等.衍射时差法(TOFD)超声波检测[M].北京:中国电力出版社,2012.

[2]CHARLESWORTH J P, TEMPLE J A G. Engineering applications of ultrasonic time-of-flight diffraction(2nd Edition)[M]. England: Research Studies Press Ltd., 2001:25-37.

[3]AL-ATABY A, AL-NUAIMY W, ZAHRAN O. Towards automatic flaw sizing using ultrasonic time-of-flight diffraction[J]. Insight, 2010,52(7):366-371.

[4]伍卫平,范钦红,曹树林,等.TOFD检测中轴偏离缺陷方位参数的测量误差[J].无损检测, 2014,36(9):28-33.

[5]李海华,赵立烦,郭兴建,等.TOFD技术检测三维盲区的分析研究[J].压力容器, 2008,125(9):4-9.

[6]强天鹏,肖雄,李智军,等.TOFD技术的检测盲区计算和分析[J].无损检测, 2008,30(10):738-740.

A New Calculation Method of the Defect Depth by TOFD in Plate Butt Welds

WU Wei-ping1, FAN Qin-hong2

(1.National Center of Quality Inspection & Testing for Hydro Steel Structure Ministry of Water Resources,Zhengzhou 450044, China;2.Zhengzhou Chenwei Science and Technology Co., Ltd., Zhengzhou 450001, China)

In view of the most wide application of TOFD in the field of plate butt welds, the article proposed a new and succinct mathematical expression of time differences to calculate the defect depth by further mathematical deduction on the basic of the conventional defect depth calculation in TOFD. The method can calculate the defect depth just only according to the time parameters read from the TOFD equipment directly and the manually input thickness of the plate. The method avoids the measurement errors of the defect depth resulted from the precision of the velocity and the value of probe center separation . Experimental verification was carried out by measuring the depths of the holes in TOFD block, the precision and feasibility of the proposed method was validated. The Experiment achieves a satisfactory result. In the end, the article discussed how to implement the thickness correction for the plate butt welds with weld reinforcement.

Time of flight of diffraction; Plate butt weld; Time differences calculation; Defect depth; Depth error; Thickness correction of the plate

2015-03-11

伍卫平(1984-)，男，工程师，硕士，主要从事无损检测及信号分析方面的工作。

10.11973/wsjc201512008

TG115.28

A

1000-6656(2015)12-0033-05