矩形开口对吸收塔结构非线性屈曲特性影响分析

宋波　牛立超　常彦斌

摘要：为了分析矩形开口参数对于吸收塔结构稳定性的影响规律，以一实际在建吸收塔结构为研究背景，基于参数化模型的正交试验，采用有限元软件ANSYS对比分析了不同开口参数下吸收塔柱壳结构的非线性屈曲特性。结果表明：开口角度对于结构的影响较其他参数大，开口角度小于90°时，结构的非线性屈曲极限荷载下降趋势较为明显，超过120°后，降幅趋于缓和，壁厚25 mm工况下，90°开口时结构的非线性屈曲极限荷载较0°开口时下降91%，120°开口时较0°开口时下降95.2%；结构的非线性屈曲极限荷载随着矩形开口高度的增加而逐渐减小，但开口位置对于结构稳定性的影响在整个过程中近似呈线性变化。

关键词：吸收塔；矩形开口；开口角度；非线性屈曲；极限荷载；稳定性

中图分类号：TU33 文献标志码：A

0引 言

吸收塔作为典型的钢制薄壁圆柱壳结构，由于工艺要求，结构上需预留矩形开口，开口破坏了结构的完整性，导致结构的受力形式变得复杂，其承载能力主要决定于结构的屈曲特性[1-2]。综合吸收塔等开口圆柱壳结构的灾害特点可知，矩形开口是影响其稳定性的重要因素，因此准确把握矩形开口参数对结构稳定性的响应规律具有重要意义。

目前，各国规范没有明确给出矩形开口对结构稳定性影响的计算公式，美国API 650规范[3]是按均匀圆柱壳验算结构的稳定性，并考虑一定的折减系数；欧盟和日本的相关容器标准[4-5]对圆形开口柱壳结构提出了相应的计算公式，但对矩形开口没有说明；中国相关规范[6-7]只给出了外压、轴向压缩荷载等作用下的光滑圆筒临界荷载计算公式，对于有开口的薄壁壳结构的设计计算至今尚无规范可循，致使此类矩形开口结构的稳定性设计存在盲点。

吸收塔结构的烟道开孔属于数学中的边值问题，目前对于圆形小孔可以确定相对完善的理论解[8]，但对于大开口，尤其是矩形开孔，由于角点处存在显著的应力集中，无法推导出完善的理论解，因此宜采用数值解法来分析开口对吸收塔结构稳定性的影响。经典线性屈曲理论[9]中，轴压下结构的应力刚度矩阵会削弱壳结构的刚度，当荷载增加时，弱化效应加强，当轴压超过某一限定荷载时，结构净刚度为0，位移无限增加，结构发生屈曲，但Toda等[10-11]试验表明，柱壳实际的临界压力比线性屈曲解析值要低得多，除了在短圆筒的情况下，通常试验值只有经典线性分叉临界值的15%～50%，这主要是由于材料非线性、轴向和环向初始缺陷、约束条件以及加载方式等因素的影响造成的。非线性大挠度屈曲分析可以确定整个壳体的平衡位形过程（后屈曲平衡位形），其荷载为下临界荷载，远低于线性临界荷载，与吸收塔结构的实际屈曲特性更加相符。

本文以一实际吸收塔为研究对象，为分析开口的影响，去除其他因素的干扰（如分段壁厚、封头、加劲肋等），建立参数化的数值模型，分析不同开口参数下吸收塔结构的非线性屈曲特点，对吸收塔结构的局部补强和壁厚分段等稳定性设计问题提出一些合理有效的建议，以强化该类结构的安全服役。

1工程背景

以贵州织金一实际在建的吸收塔结构作为研究对象，该结构高75.25 m，内径9.7 m，壁厚沿高度递减，位于13～18 mm之间，下部矩形开口高度10.5 m，开口面积16.4 m×5.4 m（开口角度为116.5°），材料为Q235钢，弹性模量E=2.06×105 MPa，泊松比为0.3，其结构尺寸如图1所示。吸收塔实际结构模型如图2（a）所示，为分析矩形开口参数对轴压下圆柱壳结构稳定性的影响规律，建立简化的参数化模型[图2（b）]，结构壁厚t简化为均匀壁厚，开口角度θ、开口位置h0、开口高度h1、塔半径r各参数如图2（c）所示。

有限元模型采用ANSYS中的Shell43单元，该单元具有塑性、蠕变、应力刚化、大变形和大应变的特性，可以很好地模拟结构的非线性屈曲过程。结构的屈服准则采用Von Mises屈服准则，钢材本构模型选用双线性各向应力同性硬化弹塑性模型，塑性硬化模量取弹性模量的1/100。图3为材料的应力-应变（σ-ε）本构模型，其中，σy为屈服应力，εy为屈服应变。

2吸收塔结构参数化模型非线性屈曲

对于吸收塔类圆柱壳结构，其线性分叉荷载是圆柱壳发生非线性后屈曲的过程中结构所能承受的最小荷载，结构的后屈曲行为通常是在结构承载力达到或接近线性临界荷载值时才发生，屈曲后结构的承载力要远小于线性临界荷载值，并发生大范围的位移，导致结构失稳。因此出于结构安全方面的保守考虑，避免结构在实际承载过程中发生的后屈曲，对结构开展非线性屈曲分析十分必要[12-15]。

分析中，首先对参数化模型开展线性屈曲分析，结构顶部轴向施加单位荷载，确定结构的屈曲特征因子，即为结构的线性屈曲特征值[16]。按照欧洲ENV 1993-1-6：1994规范[17]，假定结构按照第1阶屈曲模态形式分布引入模型初始缺陷，缺陷大小为δ/t=0.05（δ为结构最大初始缺陷值）。在结构顶部相同节点处施加屈曲特征值的1.2倍荷载，采用弧长法对结构开展非线性屈曲分析，为保证结果精确，步数适当加大，当结构以荷载子步逐渐趋近于施加荷载时，计算逐渐难于收敛而计算中断，此时结构施加的荷载即为结构的非线性屈曲极限荷载Pmax。图4为模型结构（结构总高75.25 m，壁厚t=25 mm，θ=180°，h0=20 m，h1=5 m工况）的第1阶屈曲模态（放大20倍），图5为轴压下结构非线性屈曲分析时开口处节点的荷载-位移曲线（P为荷载），其中结构的线性屈曲特征值为1.37 MN，非线性屈曲极限荷载为1.6 MN。

为了综合考虑开口参数对于结构非线性屈曲特性的影响，下面通过正交试验分析吸收塔参数化模型在不同开口角度θ、开口高度h1、开口位置h0、壁厚t等工况下结构的稳定性。

2.1开口角度对结构稳定性的影响

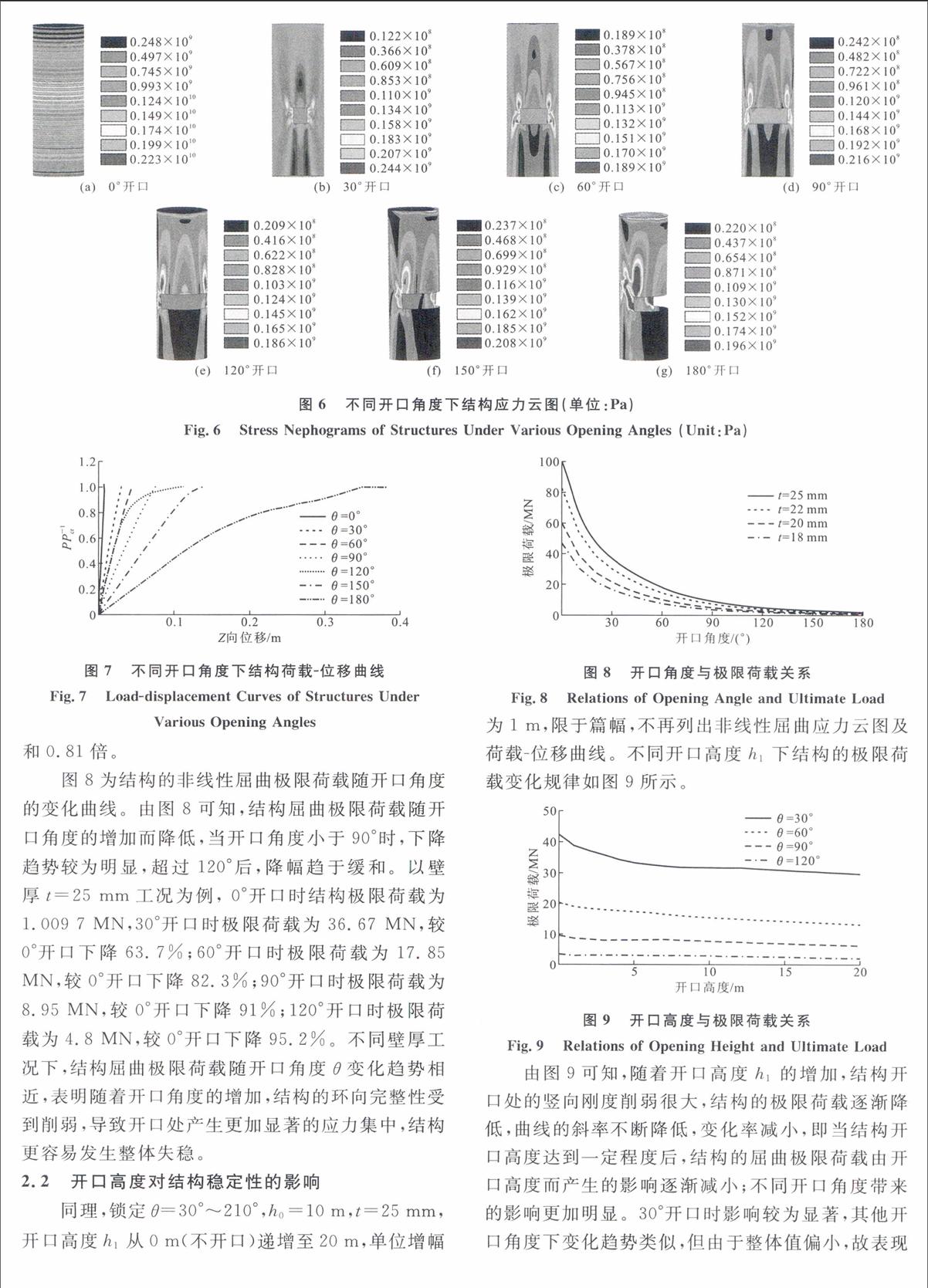
锁定其他变量（h0=10 m，h1=5 m，t=18～25 mm），开口角度θ从0°（不开口）递增至180°，增幅为10°，计算19种工况下结构非线性屈曲极限荷载随开口角度θ的变化规律，不同开口角度下结构非线性屈曲应力云图及结构开口位置处节点的荷载-位移曲线分别如图6，7所示。

由图6可以看出：开口与不开口结构表现出了不同屈曲模式，不开口时，结构变为均匀压曲；开口角度30°时，结构在开口的2条斜对角线方向的X形区域内应力变形较大，但与后续的大开口角度相比，应力影响范围较小；开口角度60°时，结构纵边界和上角点的应力集中更加显著；随着开口继续增加，结构应力集中影响区域向上扩展范围更大，对于开口角度180°这种理论工况，结构在自重下即会失稳。

由图7可知，随着结构开口角度的增加，结构的位移变形显著增加，其中，120°开口时结构开口上部节点的Z向位移为0.076 m，相对于结构0°开口（0.005 6 m）、60°开口（0.042 m）分别增加12.6倍和0.81倍。

图8为结构的非线性屈曲极限荷载随开口角度的变化曲线。由图8可知，结构屈曲极限荷载随开口角度的增加而降低，当开口角度小于90°时，下降趋势较为明显，超过120°后，降幅趋于缓和。以壁厚t=25 mm工况为例， 0°开口时结构极限荷载为1.009 7 MN，30°开口时极限荷载为36.67 MN，较0°开口下降63.7%；60°开口时极限荷载为17.85 MN，较0°开口下降82.3%；90°开口时极限荷载为8.95 MN，较0°开口下降91%；120°开口时极限荷载为4.8 MN，较0°开口下降95.2%。不同壁厚工况下，结构屈曲极限荷载随开口角度θ变化趋势相近，表明随着开口角度的增加，结构的环向完整性受到削弱，导致开口处产生更加显著的应力集中，结构更容易发生整体失稳。

2.2开口高度对结构稳定性的影响

同理，锁定θ=30°～210°，h0=10 m，t=25 mm，开口高度h1从0 m（不开口）递增至20 m，单位增幅为1 m，限于篇幅，不再列出非线性屈曲应力云图及荷载-位移曲线。不同开口高度h1下结构的极限荷载变化规律如图9所示。

由图9可知，随着开口高度h1的增加，结构开口处的竖向刚度削弱很大，结构的极限荷载逐渐降低，曲线的斜率不断降低，变化率减小，即当结构开口高度达到一定程度后，结构的屈曲极限荷载由开口高度而产生的影响逐渐减小；不同开口角度带来的影响更加明显。30°开口时影响较为显著，其他开口角度下变化趋势类似，但由于整体值偏小，故表现为曲线较平缓。

2.3开口位置对结构稳定性的影响

当开口角度θ=60°～180°，开口高度h1=5 m，壁厚t=25 mm时，对比分析开口位置h0从0 m（结构底部）递增至30 m（单位增幅为2 m）的16种工况，结构极限荷载随开口位置h0的变化规律如图10所示。

结构极限荷载随开口位置h0的增加几近于线性降低，其中开口角度为60°时，直线斜率近似为-0.248 3，开口角度为90°时，斜率为-0.150 3；开口角度为120°时，斜率为-0.087 25；开口角度为180°时，斜率为-0.029 83，即随着开口角度的增加，极限荷载-开口位置的绝对变化率降低，表现为曲线更平缓。开口高度适当时，开口所导致的应力集中会向上、向下传递分布，一定程度上对应力集中有缓解作用，而开口位置过于靠近端部会使结构更易发生局部失稳。

2.4壁厚对结构稳定性的影响

当θ=0°～180°，h1=5 m，h0=10 m时，结构壁厚t从5 mm递增至40 mm，增幅为2 mm，共11种工况。结构极限荷载随壁厚的变化规律如图11所示。

由图11可知，开口角度一定时，结构极限荷载值随壁厚的增加而增加，这主要是由于壁厚的增加对于结构整体和局部刚度都有提升。以开口角度120°为例，15 mm壁厚时结构的极限荷载较壁厚为5 mm时增加2.97倍（几近于3倍，3倍为壁厚比值），25 mm壁厚时极限值较5 mm时增加8.4倍（大于5倍，5倍为壁厚比值），35 mm壁厚极限值较5 mm时增加17.81倍（远大于7倍，7倍为壁厚比值）。由此可见，壁厚对于提高结构非线性屈曲极限荷载效果明显，可有效加强结构的整体稳定性，但是增加壁厚对于材料的使用也更多，费效比较低。因此，后续有必要开展不同加劲形式的研究，考虑补强对于结构非线性屈曲极限荷载的影响规律。图12为考虑补强作用后的吸收塔局部结构应力和位移云图。

3结语

（1）开口角度是影响柱壳结构稳定性的最主要因子，当吸收塔柱壳结构开口角度小于90°时，非线性屈曲极限荷载下降趋势较为明显，开口角度超过120°后，降幅趋于缓和，开口角度的增加对于结构的位移变化影响显著，120°开口时结构的最大Z向位移为0°开口的13.6倍，屈曲极限荷载为0°开口的4.8%。

（2）结构屈曲极限荷载随着开口高度h1的增加逐渐减小，但开口位置h0对于结构稳定性的影响在整个过程中近似呈线性变化。

参考文献：

References：

[1] 李春霞，宋 波.考虑加劲及开孔的薄钢板稳定性[J].建筑科学与工程学报，2011，28（1）：58-63.

LI Chun-xia，SONG Bo.Stability of Thin Steel Plate Considering Stiffening and Opening[J].Journal of Architecture and Civil Engineering，2011，28（1）：58-63.

[2]赵 阳，滕锦光.轴压圆柱钢薄壳稳定设计综述[J].工程力学，2003，20（6）：116-126.