多种干扰对同步直线电机伺服系统运动性能的影响

丁海波（中国船舶重工第七二三研究所，江苏 扬州　225001）

多种干扰对同步直线电机伺服系统运动性能的影响

丁海波
（中国船舶重工第七二三研究所，江苏 扬州225001）

受原有滚珠丝杠高速进给系统的限制，基于普通旋转电机基础上研制的直线电机实现了高速高精运动的控制，但是在该系统中还未配置相应的缓冲操作，导致同步直线电机伺服系统很容易受到多种干扰的影响。如果直线电机伺服系统运行过程中的任一运动部件受到影响就会出现问题，难以控制高速高精运动。因此研究多种干扰对同步直线电机伺服系统运动性能的影响，具有非常重要的意义。

直线电机；伺服系统；运动性能

0　引言

集成电路封装、纺织机械产品、数控高速加工与工艺、雷达跟踪产品等多个领域均应用到高速高精运动控制技术，该技术已经得到社会的广泛关注，对现代数控系统的发展具有极大的促进作用。但是随着对高速高精运动控制技术研究的不断加深，逐渐发现一些问题，其中最主要的就是外部干扰［1］。本研究在对直线电机伺服系统研究、分析的基础上，阐述了接地误差、电压波动与谐波、负载波动、传感器误差及负载波动对伺服系统的干扰，并以某一典型直线电机作为参考，通过仿真及实验为研究提供可靠的依据。

1永磁同步直线电机伺服系统的研究

旋转电机是直线电机形成的结构基础，在一定程度上视为沿径向将旋转电机剖开并展平的结果。本研究参考永磁同步旋转电机系统工作原理，从运动方程、磁链方程及电压方程等方面对直线电机系统进行了分析。

（1）直线电机电压方程式：

在上述直线电机电压方程中，角速度表示为Xr，线速度为Pv/S即Xr，转子相电阻表示为Rs，微分算子表示为p，极距表示为S，id、ud、Kd分别为d轴的电流、电压和磁链，iq、uq、Kq分别为q轴的电流、电压和磁链。

（2）直线电机磁链方程式：

在上述直线电机磁链方程式中，永磁磁体基波励磁磁场与定子绕组相交链的磁链表示为KPM，电机中的直轴（d轴）电感和交轴（q轴）电感表示为LS。

（3）直线电动机运动方程式：

电磁转矩公式为：

电动机的运动方程为：

在式（5）、（6）中：粘滞摩擦系数表示为B，负载阻力标示为Fl，动子和动子负荷总能量表示为M。若将动子线速度用v表示，反电动势系数用Ke表示，可以得出以下公式：

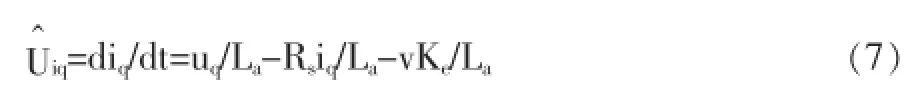
根据永磁同步直线电机的电磁转矩公式及运动方程，可以得出：

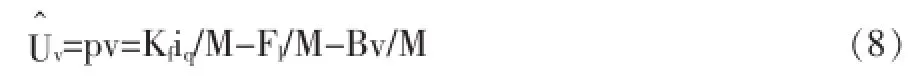
通过对式（7）、（8）的综合变形可得：

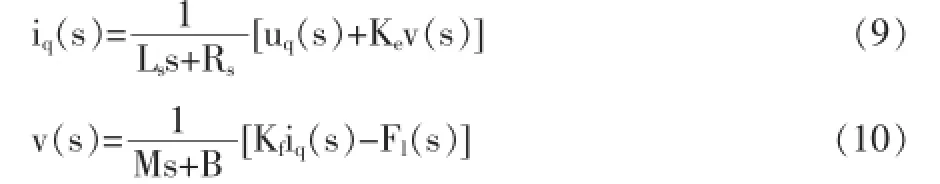
以上述整理所得的公式为基础，当粘滞摩擦系数设为零的情况下，实现多IP叠加，研究电流滞环跟踪逆变器控制［2］。同以往PI控制结构相比，在此基础上形成的IP控制的抗负载干扰性能更强，缩小了波动范围，其中Kv和Kvi分别表示IP速度环参数。永磁同步直线电机伺服系统示意图详见图1。

图1　永磁同步直线电机伺服系统示意图Fig.1 Permanent magnet synchronous linear motor servo system schematic diagram

2　永磁同步直线电机伺服系统的电机参数计算

永磁同步直线电机伺服系统框图中各个参数的意义如下：电流控制量表示为Im（s），而电流跟踪控制为Im（s）-iq（s）的过程，电流增益及电流反馈滤波时间常数分别为Kcf和Tcf，电流环开环放大系数为Kpc，电流反馈回路和逆变放大器的传递函数通过Kcf/（1+Tcfs）和KPWM/（1+TPWMs）来表示［3］。

选取丹纳赫kollmorgen Servostar系列驱动器、IL12-050A1型动子、MW0500256型定子及kollmorgen的直线电机对同步直线电机伺服系统的运动性能进行仿真，可设定永磁同步直线电机伺服系统框图中的各项数据的数值：

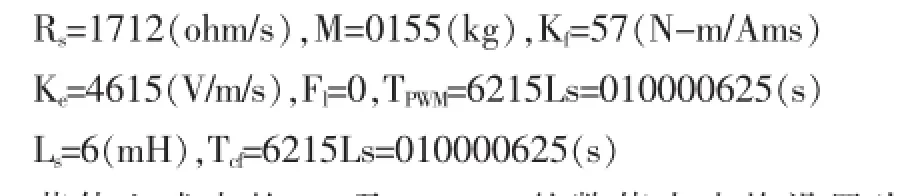
若使上式中的Kcf及KpcKPWM的数值大小均设置为10，Kv的可选取范围为1～20，而Kvi的值为20。

3　干扰同步直线电机伺服系统的主要因素

干扰同步直线电机伺服系统的主要因素有：①电磁干扰、接地误差干扰伺服系统；②电压波动、谐波对伺服系统的干扰；③负载波动对伺服系统的干扰［5］；④传感器误差对伺服系统的干扰。在本文中着重对④的干扰进行详细说明。

（1）传感器与电流采样电路方案设计。同步直线电机伺服系统达到高速高精运动的前提是要拥有高精度传感器，长光栅、圆光栅等高精度角度仪器中，对计数计算速度、分辨率等要素有严格的标准。对于光栅传感器来说，虽然制作过程中对精度进行了明确的定位，然而也有可能在组装或运行的环节出现一些问题，存在传感器误差的问题，必然会对直流电机伺服系统运动性能产生很大的影响。当光栅传感器的误差范围较小时，其虽然能够维持系统的稳定，继续发挥功能，但是还是会使反馈系统存在一些误差，导致伺服系统输出受干扰。

因为采样的精度和速度直接导致整个电流环的运算精度，从而直接对系统的性能产生非常重大的影响。而在电量参数测量领域内，霍尔电流传感器由于其稳定可靠的产品性能成为本系统设计的首选。型号为lts25-np。其具体特点和性能参数如下：原边额定电流有效值ipn：25a；原边电流测量范围ip：0～±80a；供电电压：+5v；输出电压vout：2.5±0.625v；转换率kn=np：ns为：1：2000；总精度：±0.2%；线性度：小于0.1%；反应时间：小于500ns。

该传感器有正极（+5）、测量端（out）及地（0）三个管脚。其工作原理如下：该款传感器是闭环霍尔电流传感器，使用霍尔器件作为核心敏感元件、用于隔离检测电流的模块化产品，其工作原理是霍尔磁平衡式的 （或称霍尔磁补偿式、霍尔零磁通式）。当电流流过一根长的直导线时，在导线周围产生磁场，磁场的大小与流过导线的电流的大小成正比，这一磁场可以通过软磁材料来聚集，然后用霍尔器件进行检测，由于磁场的变化与霍尔器件的输出电压信号有良好的线性关系，因此，可以用测得的输出信号，直接反应导线中电流的大小。为防止干扰，在霍尔传感器的供电电源端和地端单独并接一只1μf的退耦滤波电容。

在本系统中，由两个lem模块检测a相和b相的电流。在实际调试中，由于经过传感器出来的电流信号有高次偕波及其它干扰信号，因此必需要设计滤波器把高次偕波及其它干扰信号抑制掉。结合实际情况考虑，本文设计了带有电压跟随的二阶低通滤波器的电流检测电路。

在开关模式控制下，相电流信号含有需要滤出的高次谐波。设计中，首先利用pspice软件对滤波器进行虚拟设计［2］，经过仿真验证后，确定采用二阶的巴特沃斯滤波器结构，系统利用电流传感器检测电流，经滤波、幅度变换、零位偏移、限幅，转化为0～3v的电压信号送入dsp的a/d引脚。

电流检测及模拟二介低通滤波器设计电路中的二阶巴特沃斯滤波器 （虚线框内所示）的幅频特性曲线，通频带内的频率响应曲线最大限度平坦，截至频率为300hz，衰减斜率为-40db/dec。

（2）实验结果。实验系统中，pwm频率为15khz，死区时间为3μs，电流环采样周期为67μs，速度环采样周期为0.67ms，速度环的输出限幅值为额定电流的1.5倍，电流环的输出限幅为额定电压的1.2倍。实验控制一台8极的永磁同步电动机电机，其参数为：额定功率：1.88kw，额定转速：2500r/min，额定电流：7.5a，额定转矩：7.5nm，额定电压：220v。电机分别在 10r/min、200r/min、1000r/min、2000r/min且速度调节器参数设置为：kpv=0.5，kiv=0.02；电流调节器参数设置为：kpi=0.2，kii=0.02时的起动—停止过程的转速曲线分别如图2～5所示。

从图2～5所示的实验波形可看出当电机空载运行时，系统运行在速度电流闭环状态下，可迅速达到稳态，超调及稳态误差都很小，实验结果表明本系统设计合理，具有良好的动静态性能。

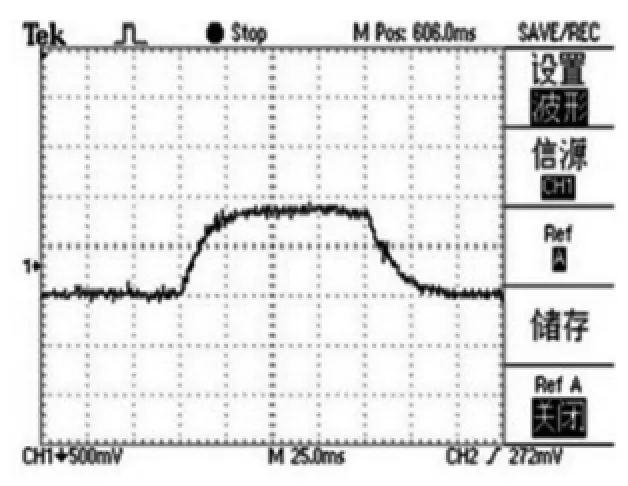
图2　10r/min起动-停止曲线Fig.2 10r/min start-stop diagram

图3　200r/min起动-停止曲线Fig.3 200r/min start-stop diagram

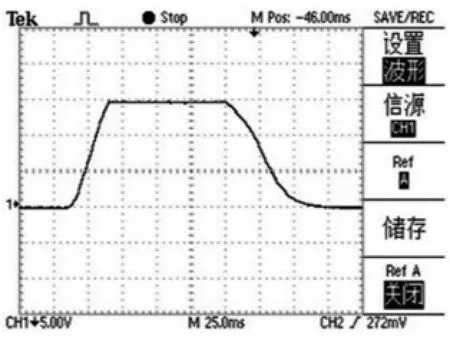
图4　1000r/min起动-停止曲线Fig.4 1000r/min start-stop diagram

图5　2000r/min起动-停止曲线Fig.5 2000r/min start-stop diagram

4　直线电机伺服系统运动性能的仿真与试验

为了更清晰的显示不同干扰因素对直线电机伺服系统运动性的影响，下面主要进行了一些仿真和试验研究。试验中系统模拟输入端电压为-10V—+10V，电机速度最大值为2125m/s，当输入端电压为+10V时，相应正方向速度为2125m/s，该仿真将输入速度设为10m/s。，详见图6。

（1）电压波动、谐波对伺服系统的干扰仿真。进行仿真时，将施加uq的干扰设置为-5%uq～+5%uq，结果显示：kv为最小值时，即为1～5时，误差最大，而kv为最大值时，即为10～20时，误差最小，kv为最小值时系统时，系统输出详见图6。图中30～40s时施加电压扰动，输出变化为0.9m/s～1.1m/s。

（2）电磁干扰、接地误差对伺服系统的仿真。试验中系统模拟输入端感应电压同接地误差值为30mV，相应输入速度为0.00675m/s，在30～40s时刻叠加到图7中的输入端，仿真结果详见图8。在30mV叠加误差中的结果显示，输出速度波动范围为0.993～1.007m/s。

（3）负载波动对伺服系统的干扰仿真。当电机系统，在 30～40s时受到矩形波外力扰中值为10N，系统输出仿真结果详见图9，输出值变化范围为0.93～1.07m/s。

（4）传感器误

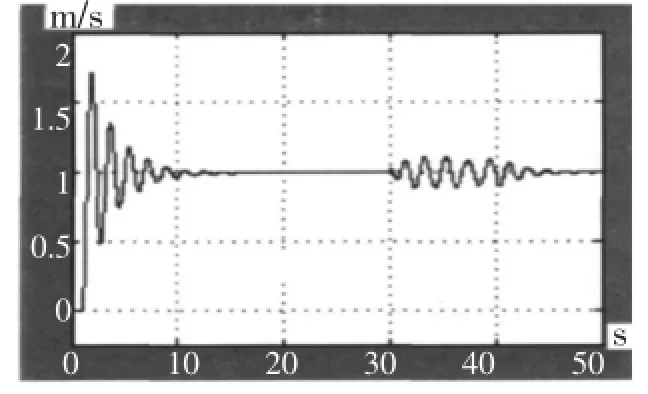
图6　电压波动对系统输出的干扰Fig.6 System interfered by voltage fluctuations

图7　电磁干扰、接地误差对系统输出的干扰Fig.7 System output interfered byelectromagnet interference and earth error

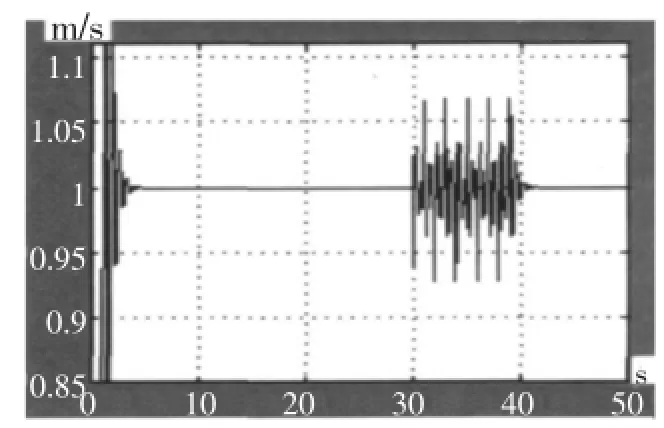
图8　负载波动对系统输出的干扰Fig.8 System output interfered by load fluctuation

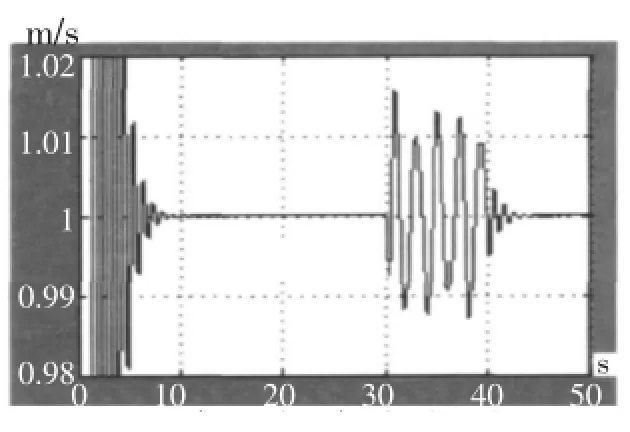
图9　传感器误差对系统输出的影响Fig.9 System output interfered by sensor error

差对伺服系统的干扰仿真。当传感器存在1%的误差时，图6中反馈回路中叠加误差范围为-0.01～+0.01m/s，系统的输出结果详见图9。在30～40s时受到误差影响，导致输出误差增大，范围为-0.012～+0.012m/s。

5　结束语

本研究在对直线电机伺服系统研究、分析的基础上，阐述了接地误差、电压波动与谐波、负载波动、传感器误差及负载波动对伺服系统的干扰，并以某一典型直线电机作为参考，通过仿真及实验为研究提供可靠的依据。

［1］张从鹏，刘强.直线电机气浮精密定位平台设计与控制［J］.北京航空航天大学学报，2008，2.

［2］王明杰，程志平，焦留成.永磁直线电动机的稳态参数计算分析及有限元验证［J］.微特电机，2014，7.

［3］韩江，苏志远.直线电机进给伺服系统的自适应模糊位置控制研究［J］.合肥工业大学学报（自然科学版），2008，1.

［4］蔡满军，赵成圆.永磁直线同步电机的自适应迭代学习控制［J］.微特电机，2014，6.

［5］张国柱，陈杰，李志平.直线电机伺服系统的自适应模糊摩擦补偿［J］.电机与控制学报，2009，1.

Multiple Interference on the Motion Performance of Synchronous Linear Motor Servo System

DING Hai-Bo
（723 Institute CSIC，Yangzhou Jiangsu 225001，China）

Restricted by the original high-speed ball screw feed system，the linear motor realized the high speed and high precision motion control which based on the general rotary motor，but in the system still don't configure corresponding buffer action，which make the synchronous linear motor servo system easily affected by multiple interference.It can be problem if any moving parts affected in the process of linear motor servo system，it is difficult to control the high speed and high precision motion.So it have great significance to study the multiple interference on the motion performance of synchronous linear motor servo system.

linear motor；servo system；motion performance

TH-39

Adoi：10.3969/j.issn.1002-6673.2015.05.042

1002-6673（2015）05-113-04

2015-06-30

丁海波（1989-），男，江苏南通人，大学本科，助理工程师。研究方向：机电一体化。