钛合金薄板Lamb波检测的有限元分析

张博南,霍宇森，吴　迪，滕永平，吴海燕

(1.北京有色金属研究总院，北京 100088；2.北京交通大学 理学院，北京 100044)



钛合金薄板Lamb波检测的有限元分析

张博南1,霍宇森2，吴迪2，滕永平2，吴海燕1

(1.北京有色金属研究总院，北京 100088；2.北京交通大学 理学院，北京 100044)

超声Lamb波广泛应用于板状材料的无损检测领域。半解析有限元法是求解导波在复杂介质中频散问题的一种计算方法。利用半解析有限元法推导了Lamb波在大型TC4钛合金薄板中传播的理论模型，分析了导波的特点，并选取S0模式对钛合金薄板进行了人工缺陷检测。实验选取S0模式的导波分别对深度为钛合金板厚5%和10%的缺陷进行线性扫描检测,结果显示在有缺陷的地方会出现明显的回波信号。结论表明,Lamb波传播距离远，且覆盖整个金属板，可用于大型板材缺陷的无损检测。

兰姆波；有限元分析；超声波检测

钛合金是一种比较难加工的特种材料，具有强度高且密度小，力学性能好，韧性和抗蚀性强的优点,是航空航天和兵器工业中广泛使用的一种重要的新型结构材料。但是,钛的工艺性能差，抗磨性能低，切削加工困难，钛合金薄板在加工过程中非常容易吸收杂质或产生划伤、结疤、气孔、夹层等缺陷，导致表面出现夹杂物或凹坑等质量问题[1-3]。

钛合金薄板在实际缺陷检测时,通常采用C扫描成像法。该方法速度慢，效率较低，检测大型工件较费时。而导波能在介质中长距离传播，采用线扫描方法可实现对大型钛合金板表面或内部缺陷的快速检测。目前,导波已成为超声检测领域研究的热点，主要应用于大型板壳、管道和铁轨的检测[4-6]。

笔者利用半解析有限元法，着重对TC4钛合金薄板中导波的特性、理论模型进行分析,并对缺陷进行检测试验与验证。

1　导波的传播特性

导波是波在竿、管、板等结构的波导介质中传播时，不断地与介质的上下边界发射折射、反射及纵波与横波之间的波型转换作用而产生的波[7]。由于边界条件的引入，使得导波具有频散性和多模态性两个重要特性。频散曲线是用来描述和预测相速度、群速度、模态和厚度关系的曲线。多模态是指导波以多种模式在波导内传播的特性,在板中可将导波分为对称模态和反对称模态两大类[7]。对频散方程的求解、频散曲线的绘制和分析是理解无损检测中导波的激发、接收和缺陷判别的基础[8]。利用导波检测工件缺陷时，回波信号不仅与缺陷有关，还与导波的模式有关。

2　半解析有限元法分析钛合金板Lamb波的传播特性

利用半解析有限元法分析钛合金板中Lamb波的传播特性时，将钛合金板看作截面为任意形状的无限宽板模型，依次对其进行离散、组装、求解。首先计算离散单元的刚度矩阵和质量矩阵，接着对单元刚度矩阵和单元质量矩阵进行标准有限元组装，得到整体刚度矩阵和整体质量矩阵，然后根据虚功原理推导出介质的波动方程，最后将整体刚度矩阵和整体质量矩阵代入波动方程进行求解。

假设板截面为oxy，导波沿着z方向传播，波数为ξ，频率为ω，波导中每个点的简谐位移分量u、应力分量σ、应变场分量ε分别可以表示为：

(1)

(2)

(3)

假设传播方向z的位移场是简谐的，空间分布函数用来描述oxy平面内截面位移场的振幅变化：

(4)

(5)

式中:N为形函数矩阵;q(e)为单元节点位移函数。

根据哈密顿原理，可得到单元刚度矩阵和单元质量矩阵，利用标准有限元法对单元矩阵进行组装可得到均匀介质的波动方程[9-15]：

(6)

式中:K1、K2、K3为整体刚度矩阵;M为整体质量矩阵;U为未知节点位移的全局矢量;下角标Q表示系统自由度数目。

引入辅助矩阵化简波动方程，最终的特征值问题可以写为：

(7)

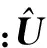
通过MATLAB编程求解本征值问题可以获得波数，从而得到波数和频率的关系，进而绘制Lamb波的相速度频散曲线。求解一系列不同波数对应的复杂特征值问题，获得相应的频率即可绘制Lamb波的群速度频散曲线。

图1为利用MATLAB编程绘制的TC4钛合金薄板中Lamb波的相速度、群速度频散曲线，其中该板板厚为0.278 mm，拉力试验测得钛合金薄板的弹性模量为106 GPa，泊松比为0.34，密度为4 430 kg·m-3,换能器发射频率为4.0 MHz。

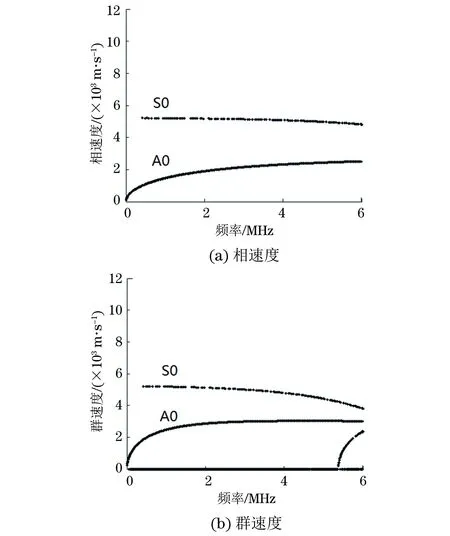
图1　钛合金薄板中的相速度与群速度频散曲线

3　模态选择

常用的超声Lamb波检测模态为零阶对称模态(S0模态)和零阶反对称模态(A0模态)。这两种模态的激励对于传感器有不同的要求：激励A0模态时，要求激励源离面位移为主，利用常用的压电换能器就能实现；激励S0模态时，要求激励源面内位移为主，较难实现。由于A0模态的易激励性，工程上常采用其进行检测，但A0模态衰减较大，而且对板表面附着物很敏感，在整个板厚方向无法实现一致的灵敏度，故在很多检测过程中并不适用。而S0模态即使板表面有负载时，其衰减也很小。根据S0模式的幅值最大而其他模式幅值相对较小时所对应的频率，即可识别出Lamb波S0模式优化的激发频率；然后调节频率，仅通过选择合适的激发频率，采用单面激励的方法即可获得优化的S0模式[16]。但是文中试验所用换能器的中心频率是固定的，因此选用的是未经优化的S0模式，通过其相速度频散曲线计算探头的发射角，对钛合金薄板的缺陷进行检测。当然，在选择检测模态时，必须考虑前面所述缺陷的类型。对于不同的缺陷，根据不同的波结构选择对被测缺陷比较敏感的模式。如为内部缺陷，应选择面内位移分量比较大的模式；若为表面缺陷，则应选择离面位移分量比较大的模式。

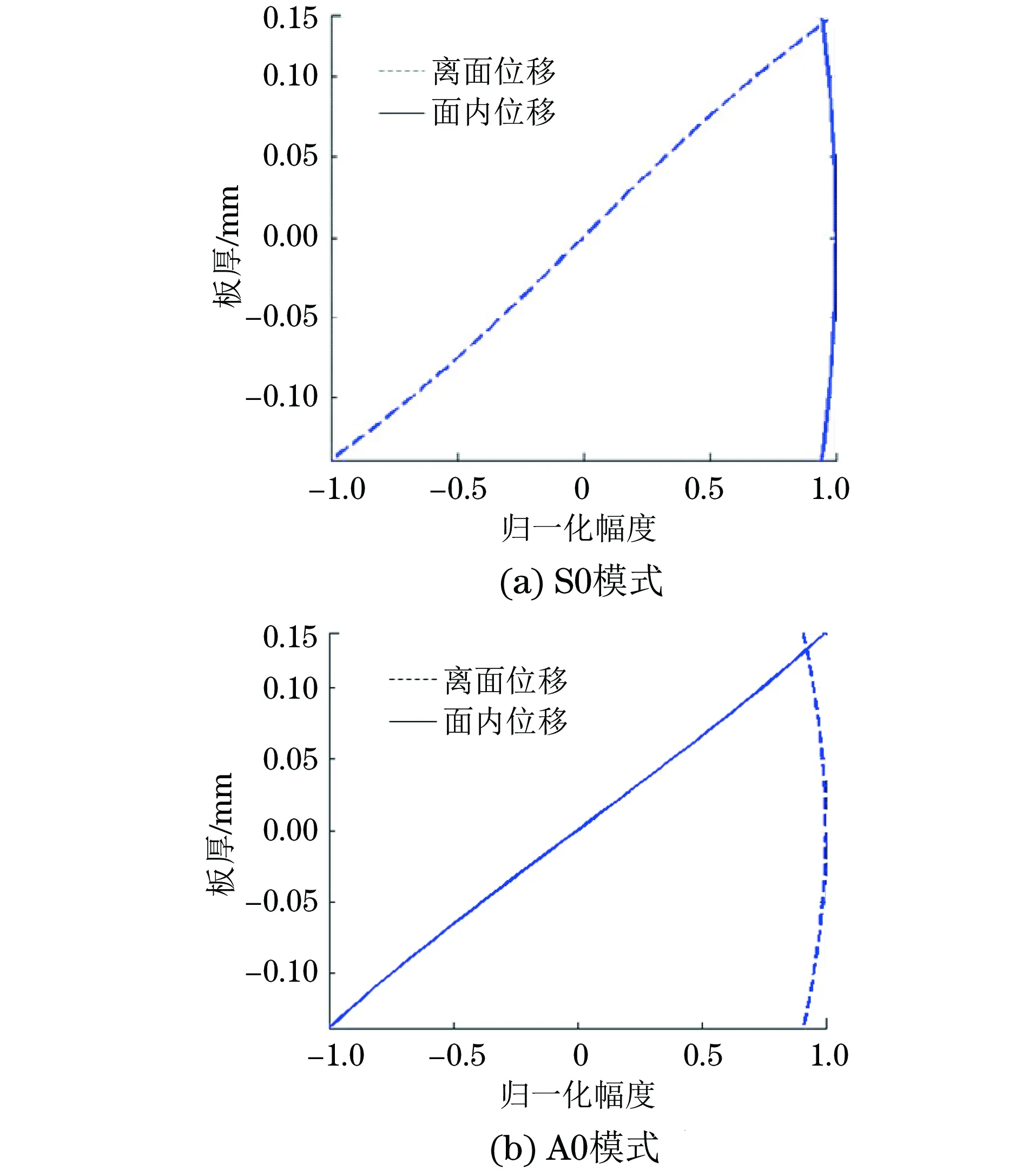
图2　钛合金薄板中S0和A0模式导波在板厚方向的位移分布(频厚积1.112 MHz·mm)

当被检测结构缺陷情况复杂时，有时候需要使用多种模式对材料结构的不同缺陷进行检测。文中所用探头的中心频率为4 MHz，钛合金薄板的厚度为0.278 m，则频厚积为1.112 MHz·mm。从图2可看出，对S0模式来说，在板的表面，面内位移分量比较大，离面位移相对较小；对A0来说，离面位移分量比面内位移分量大。

4　导波激励

利用可变角探头激励导波，如图3所示,将探头放置在板的一端A，由超声发射接收仪激发导波，导波沿着钛合金薄板传播，在板的另一端B反射回来被探头接收。查阅图1(a)所示的钛合金薄板的相速度频散曲线，找到激励频率为4 MHz时对应的相速度cp，可变角探头的发射角θ应满足Snell定理[17]，即：

(8)

由此即可算出可变角探头的发射角。

5　缺陷检测

试验时，钛合金板可看作无限大，上面一端刻有厚度为5%，10%板厚的细缝，另一端有不同大小的两个通孔。试验所用超声脉冲发射接收装置为DG1022函数信号发生器，示波器GOS-620，探头为德国某公司的MUWB 4-N型可变角探头，频率4 MHz，采用单探头发射和接收板端回波。试验系统结构示意如图3所示。接下来的所有试验中，信号发生器型号为RIGOL-DG1022，峰峰值电压为20V,方波脉冲个数为3，频率为4 MHz。

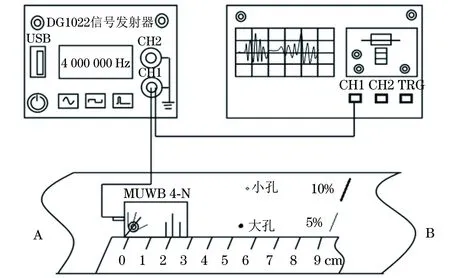
图3　试验系统结构示意

5.1模式激发和判断

从钛合金板的频散曲线图(图1)可看出，S0模式的传播速度相对A0模式的要快。而且对于细缝，S0模式的面内位移分量相对比较大，而A0模式的离面位移分量比较大，所以选择S0模式来检测钛合金板缺陷。对于通孔，虽然其半径很小，但鉴于板的厚度非常小，所以也可用S0模式检测通孔的存在。有机玻璃斜楔的纵波速度为2 740 m·s-1，从图1所示的相速度频散曲线中可查得S0模式的相速度约为5 214.29 m·s-1，代入Snell定律可计算得到，超声波的入射角为31.7°。

将探头放置在经过较大通孔的直线上，距离通孔20 mm, 通孔的反射回波如图4(a)所示。同样，也可在示波器上同时看到较大通孔和钛合金薄板板端的回波，更好地证明可采用这种方法进行板中通孔类缺陷的检测，其回波信号如图4(b)所示。

图4　较大通孔、较大通孔与板端的反射回波

由图4(b)可算出始波到缺陷反射回波的传播时间为8.39 μs;由式cg=ΔL/Δt计算群速度，式中ΔL为Lamb波的传播距离，Δt为Lamb波的传播时间，则:

而从图1(b)所示的群速度频散曲线可得到S0模态理论模拟的群速度值为4 792.79 m·s-1，误差为0.52%，所以该Lamb波的主要模式为S0模式。

5.2不同大小缺陷检测

将探头放置在经过较小通孔的直线上，接收到的缺陷回波信号如图5所示。对比图4(a)和图5所示的不同深度缺陷的回波信号可看到，较小通孔的反射回波的幅度小于较大通孔的反射回波幅度，这表明导波可以用于钛合金薄板中通孔类缺陷的检测，通过反射回波信号可检测到缺陷的存在，并定性地判断其相对大小。

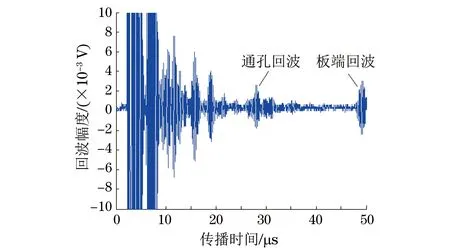
图5　较小通孔的反射回波

5.3刻槽的检测

首先,将探头放置在经过深度为5%板厚度刻槽的直线上，来回移动探头的位置，在示波器上找到刻槽所对应的回波信号，如图6(a)所示。然后，将探头放置在垂直于10%板厚度刻槽的直线上，来回移动探头，可在示波器上观察到刻槽的反射回波，如图6(b)所示。由图6可看出，用检测通孔时选取的导波模式，同样可检测到钛合金表面刻槽类缺陷的存在。

图6　5%，10%板厚的人工槽的反射回波

5.4试验结果分析

从试验得到的波形可看出，导波可实现长距离的缺陷检测。若选取合适的模式，在有缺陷的地方会出现明显的回波信号。根据缺陷回波与探头间的距离和传播时间差，可计算出缺陷的位置。观察不同深度刻槽或者不同半径大小通孔的缺陷回波的信号幅值，可看出，缺陷越大，回波信号幅值越大。

6　结语

利用半解析有限元法可以分析钛合金板中Lamb波的传播特性，得到相速度、群速度频散曲线和多个传播模态，并从中选择钛合金薄板缺陷检测的最佳模态，指导换能器的设计和实际检测。由于Lamb波具有频散性和多模态性，导致实际应用受到限制，故具体的检测中，需要先找到检测的最佳模态，尽可能地激发单一模式的导波，并采用更加精密的传感器，才能取得良好的检测效果。

[1]李梁, 孙健科, 孟祥军. 钛合金的应用现状及发展前景[J]. 钛工业进展, 2005, 21(5): 19-24.

[2]付艳艳, 宋月清, 惠松骁, 等. 航空用钛合金的研究与应用进展[J]. 稀有金属, 2007, 30(6): 850-856.

[3]钱九红. 航空航天用新型钛合金的研究发展及应用[J]. 稀有金属, 2000, 24(3): 218-223.

[4]冯占英, 周正干, 高翌飞.大型薄板中超声导波的产生与鉴别[J]. 无损探伤, 2007, 31(5).

[5]周正干,冯占英,高翌飞,等. 超声导波在大型薄铝板缺陷检测中的应用[J]. 航空学报, 2008, 29(4): 1044-1048.

[6]何存富, 周进节, 吴斌,等. 管道导波时反聚焦检测系统的设计与实现[J]. 仪器仪表学报, 2012, 33(2): 342-348.

[7]丁辉.计算超声学[M]. 北京:科学出版社, 2010:102-103.

[8]邹宁波,谌海云,刘全利,等.基于T(0,1)模态超声导波的输气管道腐蚀检测[J].无损检测，2013，9(35):19-22.

[9]曹志远,张佑启.半解析数值方法[M].北京:国防工业出版社,1992:1-60.

[10]HAYASHI T, SONG W J, ROSE J L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example[J]. Ultrasonics, 2003, 41(3): 175-183.

[11]LOVEDAY P W. Guided wave inspection and monitoring of rail track[J].Nondestruct Eval,2012,31(4):303-309.

[12]ROSE J L, AVIOLI M J, MUDGE P, et al. Guided wave inspection potential of defects in rail[J].NOT&E International,2004,37(2):153-161.

[13]MOSER F, JACOBS L J, QU J.Modeling elastic wave propagation in waveguides with the finite element method[J].NDT&E International,1999,32(4):225-234.

[14]RYUE J, THOMPSON D J, WHITE P R, et al. Investigations of propagating wave types in railway tracks at high frequencies[J]. Journal of Sound and Vibration,2008,315:157.

[15]HAYASHI T, SONG W J, ROSE J L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example[J].Ultrasonics, 2003,41(3):175.

[16]张海燕, 曹亚萍, 于建波, 等. 采用单个压电传感器的单模式兰姆波激发频率的选择[J]. 物理学报, 2011, 60(11): 377-385.

[17]李鸿源，徐鸿.基于压电晶片的超声导波激发特性试验[J]. 无损检测，2013，35(1): 22-26.

Finite Element Analysis of Testing of Titanium Alloy Thin Sheet Using Lamb Wave

ZHANG Bo-nan1, HUO Yu-sen2, WU Di2, TENG Yong-ping2, WU Hai-yan1

(1. General Research Institute for Nonferrous Metals, Beijing 100088, China;2. School of Science, Beijing Jiaotong University, Beijing 100044, China)

Ultrasonic Lamb wave is widely used in nondestructive testing of the plate material. In this paper, the theoretical model of Lamb wave propagating in the large TC4 titanium alloy sheet was derived using the semi-analytical finite element method to solve the dispersion equation of guided waves in complicated medium, followed by the analysis of the characteristics of guided wave and the test of the artificial defects in titanium alloy sheet using S0 mode. The liner scan was performed using S0 mode guided wave for the defects of titanium alloy sheet which were of 5% thickness and 10% thickness in the experiment. The result showed there was strong echo signal where artificial defects existed. So Lamb wave can be used in nondestructive testing of defects in large titanium plates with the advantages of long propagation distance and large detection range.

Lamb wave;Finite element analysis;Ultrasonic testing

2015-03-20

张博南(1989-),男,助理工程师,硕士,主要从事超声、涡流无损检测相关工作。

10.11973/wsjc201510015

TB559; TG115.28

A

1000-6656(2015)10-0064-05