各向同性材料的强度校核在Matlab中的实现

李昕，沈斌（同济大学 中德学院，上海 201804）

各向同性材料的强度校核在Matlab中的实现

李昕，沈斌
（同济大学 中德学院，上海 201804）

在汽车设计生产中，为了能高效及时的分析车身材料的特性及其之间相互影响的关系，需要开发一款利用Matlab评估材料特性的软件。论文介绍了由各向同性材料制成的具有不同截面的杆件在受到多个线性叠加外部静载荷时强度校核的方法以及应力集中现象对强度的影响；其次简述了该强度校核过程在Matlab中实现的算法思路以及主要的算法流程；最后对软件计算结果和实际工程应用中的计算结果进行比较和误差分析，保证计算结果的可靠性。该算法的实现保证了汽车在实现轻量化生产的同时并没有损失其必要的安全性。

各向同性；强度校核；Matlab编程

0　引言

在汽车设计生产过程中，为了保证汽车安全性能和舒适度，需要对车身材料的性能，结构及其之间相互影响的关系进行研究分析。因此有必要开发一款利用计算机对材料性能以及各性能之间的关系进行有效评估的软件系统。这款软件系统是基于Matlab的编程语言开发实现的，同时材料强度是评定材料性能时最重要的标准之一，在汽车车身制造中各向同性材料也占有重要的位置。因此本文着重研究了各向同性材料的强度校核在Matlab中的实现。

本文实现了利用Matlab对不同截面的杆件或梁在线性叠加的静载荷下的强度计算，并分析了应力集中现象对强度的影响，最后将Matlab计算出来的结果和实际计算结果进行了比较和误差分析。

1　理论基础

1.1单一载荷下的应力计算

强度是指某种材料或者由某种材料制成的构件抵抗断裂或永久变形的能力。杆件最常见的四种基本变形为：拉压，剪切，弯曲，扭转。杆件受拉压和弯曲所产生的应力为正应力，受剪切和扭转所产生的应力为剪切应力。

杆件受到拉压应力的大小等于其单位横截面积上所受的轴向力的大小。受到切应力大小等于其单位剪切面积上所受剪切力的大小。杆件上某位置的最大弯曲应力为此位置引起形变的弯矩Mb与此截面的抗弯截面模量W的比值。杆上某位置的扭转应力等于该位置所受扭矩Mt与该截面的抗扭截面模量Wp的比值。表1中列出了杆件分别受到四种基本变形后产生的应力计算公式。

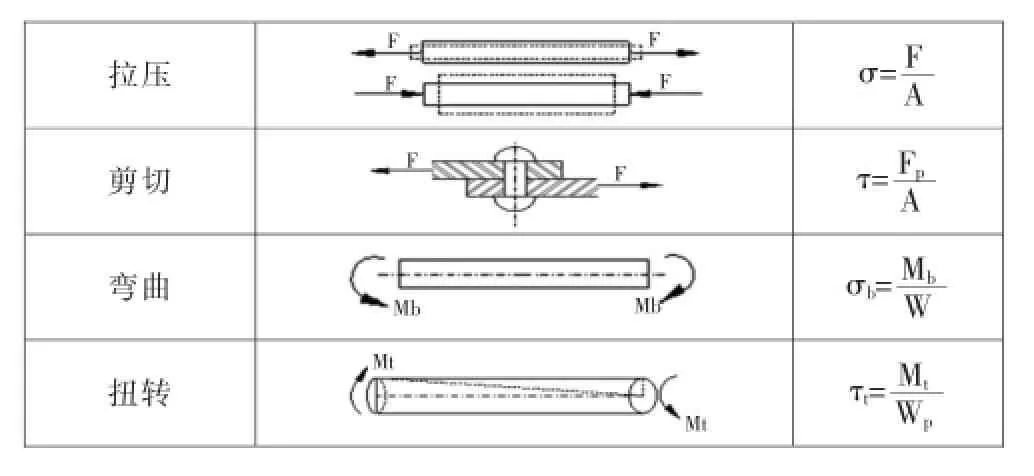
表1　单一载荷下杆件应力计算公式Tab.1 Stress calculation formula ofrods underthe single loads

1.2截面形状及相关几何量

根据表1中的公式，要计算杆件在外力作用下产生应力的大小，不仅需要外部载荷，还要计算截面面积，抗弯和抗扭截面模量。这些根据杆件截面形状及尺寸推导得出的量称为与截面相关的几何量。要确定这些几何量的大小，就要先确定待研究的截面形状。根据在汽车中常见杆件和梁的截面形状分析，确定六种截面为主要研究对象，即椭圆，长方形，I型，T型，Z型和U型截面。其他截面均可由此六种形状推导得出。抗弯截面模量W和抗扭截面模量Wp是两个分别用于计算截面上产生的最大弯曲应力和扭转应力的几何量。它们可以分别通过计算轴惯性矩I或极惯性矩Ip与在横截面上离中性轴最远的点和中性轴间的距离amax的比值得出：

1.3载荷形式

杆件所受的弯矩是计算弯曲应力时一个重要的物理量。它与梁的类型以及所受弯曲载荷的形式有关。本文中主要研究常见的简支梁和悬臂梁。对每种梁又分别研究了五种外部载荷类型，见表2。根据每种梁在不同载荷下的受力分析可以求出其关于梁长x的弯矩方程，此弯矩方程的极值，即为梁所受的最大弯矩的位置及大小，由此可求出所产生的最大弯曲应力。

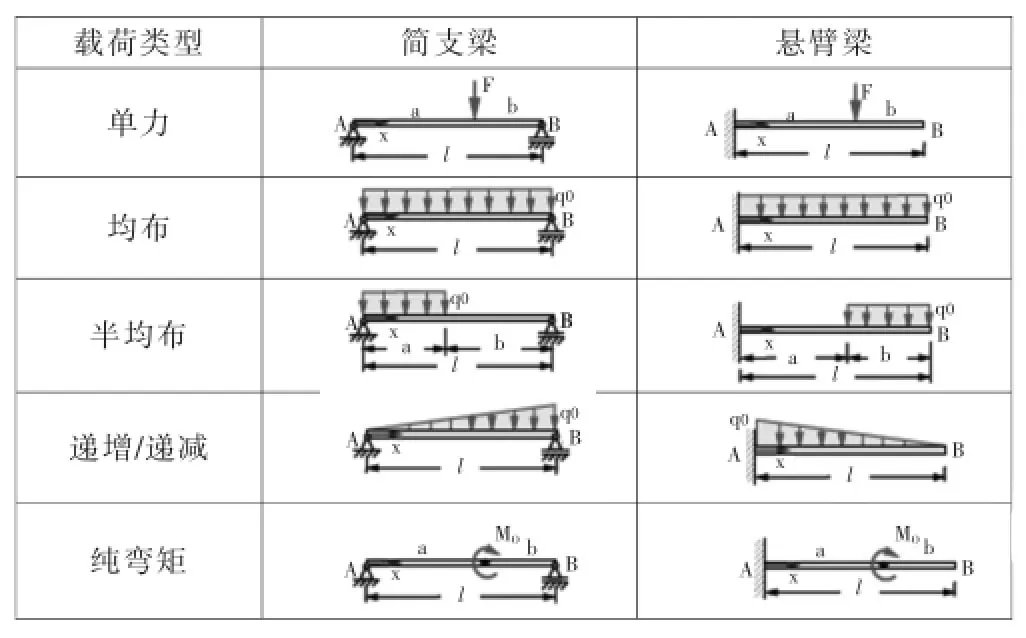
表2　引起简支梁和悬臂梁发生弯曲变形的五种载荷形式Tab.2 Five load forms that cause the bending deformation of simply supported beam and cantilever

1.4胡克定律和强度理论

根据胡克定律，当材料处于线弹性变形范围内时，其变形所产生的应力σ，τ与应变ε，γ成线性比例关系，比例系数为弹性模量E或剪切模量G：

要校核杆件的强度还需合适的强度理论作为基础，常用的强度理论有最大拉应力，最大切应力以及形状改变比能理论。最大拉应力理论认为材料发生脆性断裂的主要原因是最大拉应力σ1达到极限值σb，它用于校核脆性材料发生断裂破坏时的强度。其强度条件：

式中：S—安全系数；［σ］—许用拉应力。最大切应力理论用于校核塑性材料发生塑性流动破坏或者滑移断裂时的强度。理论上认为无论构件处于何种应力状态，构件危险点的最大切应力τmax达到了材料在单向拉伸屈服时的极限剪应力τ0，是发生塑性流动的主要原因。由于：

用主应力表达的最大切应力理论的强度条件为：

式中：σ1，σ3—构件危险点的最大和最小主应力；σ—材料屈服极限。形状改变比能理论认为：塑性材料发生屈服的主要原因，是构件危险点的最大形状改变比能达到了一个极限值。该理论用主应力表达的强度条件为：

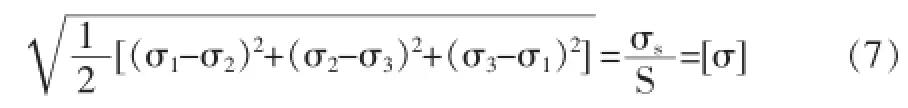
式中：σ1，σ2，σ3—构件危险点的主应力。将这三个强度理论分别用应力转换公式转换为用拉压应力，弯曲应力和扭转应力表达的平面应力状态下的强度条件公式如下：

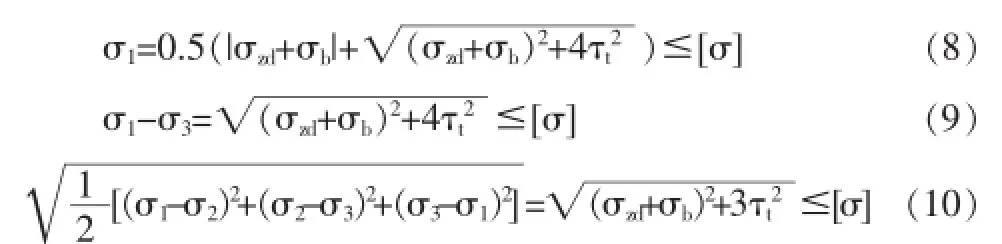
式中：σzd—构件危险点的最大拉或压应力；σb—构件危险点的最大弯曲应力；τt—构件危险点的最大扭转应力。通过计算杆件受到线性叠加的合成载荷下所产生最大拉压应力，弯曲应力及扭转应力，判断其可能的失效形式后通过相应的强度理论，可以对杆件的强度利用公式（8）～（10）进行校核。

1.5应力集中现象

在实际工程中所使用的杆件往往是经过开槽，挖孔，做轴肩后的杆件。这会使杆件的横截面积尺寸发生局部突变。根据实验可得，在尺寸发生突变的横截面应力分布是不均匀的。从图1可以看出，应力在孔和凹槽的边缘发生急剧升高，这种由于尺寸变化引起局部应力增大的现象叫做应力集中现象。

应力集中系数αk可以反映出杆件在静态外载荷作用下应力集中的程度，它是应力集中处的最大应力 σmax与净截面上的平均应力σn的比值：

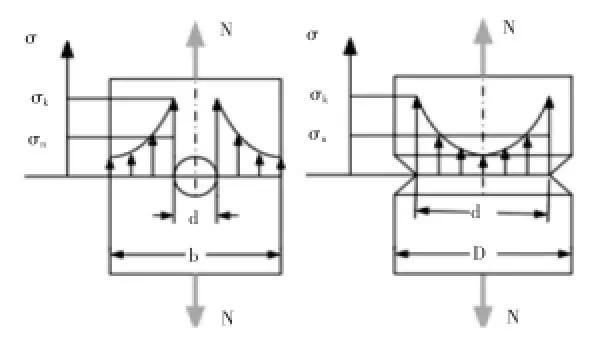
图1　圆孔和凹槽处的应力集中现象Fig.1 Stress concentration at the hole and the groove

应力集中系数与构件的材料无关，而与切槽的深度，孔的大小以及变截面的过渡圆弧大小有关。表1中所罗列的应力计算公式均用于计算等直杆在静载荷作用下净截面上的平均应力大小，在进行强度校核时，还需要考虑到应力集中现象，求得应力集中处的最大应力，再通过强度理论求得用于与许用应力进行比较的比较应力。常见几种构件的应力集中系数，可以在相关的工程手册中查询。

2　强度计算在Matlab中的实现

2.1计算总流程

利用Matlab实现强度计算时，首先要根据构件所受外部载荷的种类及大小分别计算出最大拉压，弯曲和扭转应力。但此应力仅是构件净截面上所受的最大平均应力。因此还必须要考虑到实际工程的应力集中现象。各应力分别乘以相应的应力集中系数，即可获得应力集中现象下的截面最大应力。将计算得出的最大应力带入合适的强度条件公式中，即可得出比较应力。如果比较应力没有超过材料的许用应力，即可说杆件在这种外部载荷下满足强度条件，强度足够。计算总流程见图2。

2.2最大合成应力的计算

为了求出构件净截面的最大平均应力，要首先分别求出构件危险截面的所受外部载荷的大小。想要求出净截面上最大拉压应力的大小，可根据胡克定律将可以引起拉压应力的外部载荷（拉/压力）线性叠加，求出合成载荷，然后根据表1中的应力计算公式计算构件的合成应力的大小。用同样的方法对构件所受的扭矩进行叠加然后利用表1中的公式，也可以求得合成扭转应力的大小。

但要计算构件所受的最大弯矩要先在程序中确认梁的种类，其次要分析引起弯曲应力的外部载荷。这些外部载荷可以根据胡克定律分解为单一的外部载荷，每种单一外部载荷都有对应的关于梁长x的挠度和弯矩方程，将这些单独的弯矩方程线性叠加之后便得到了一个关于梁长的总弯矩方程。利用 Matlab程序语言求出这个方程在梁长范围内的极值，即为梁所受最大合成弯矩，然后利用弯曲应力计算公式，可以求出净截面在受多个线性叠加外载荷时产生的最大弯曲应力的大小。计算合成弯曲应力的算法流程如图3所示。

图2　在Matlab中实现强度计算的总流程图Fig.2 Master Flowchart of the strength calculation with Matlab

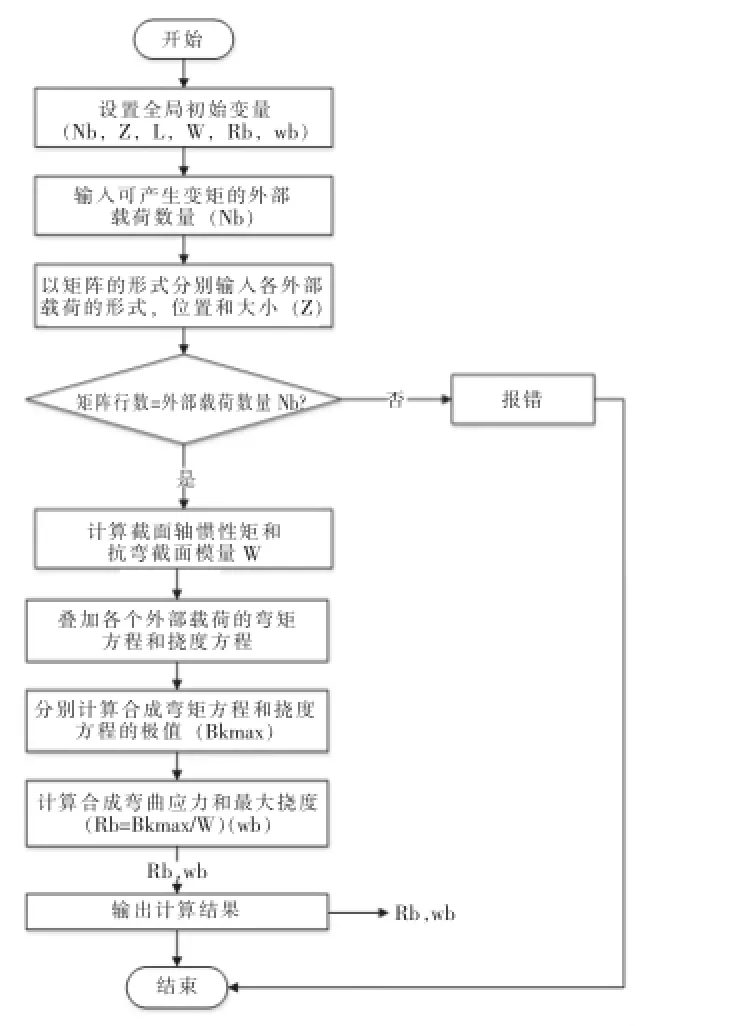
图3　计算合成弯曲应力的算法流程图Fig.3 Algorithmic Flowchart of the calculation of resultant bending stress

2.3应力集中系数的计算

应力集中系数一般可以根据构件尺寸，应力集中类型和受载荷形式在应力集中系数曲线上读出。但在Matlab中这种方式效率低下并且不易于代码的实现。观察常见的应力集中系数曲线可以发现，这些曲线可以归纳为关于构件尺寸和危险截面尺寸的方程。利用这些方程，就可以在Matlab中计算出近似的应力集中系数。

文献［4］中给出了通过实验和数值分析方法进行验证得出的应力集中系数近似方程。通过近似方程计算得出的应力集中系数和图表读取的应力集中系数有大约10%的误差，但这样的误差精度对于我们强度校核的影响是很小的，于是在Matlab实现过程中，使用了近似方程进行应力集中系数的计算。

表3是文献［4］中给出的其中一个近似方程。它用于计算方形杆和圆形杆在具有切槽和轴肩时分别受拉压、弯曲和扭转时的应力集中系数。

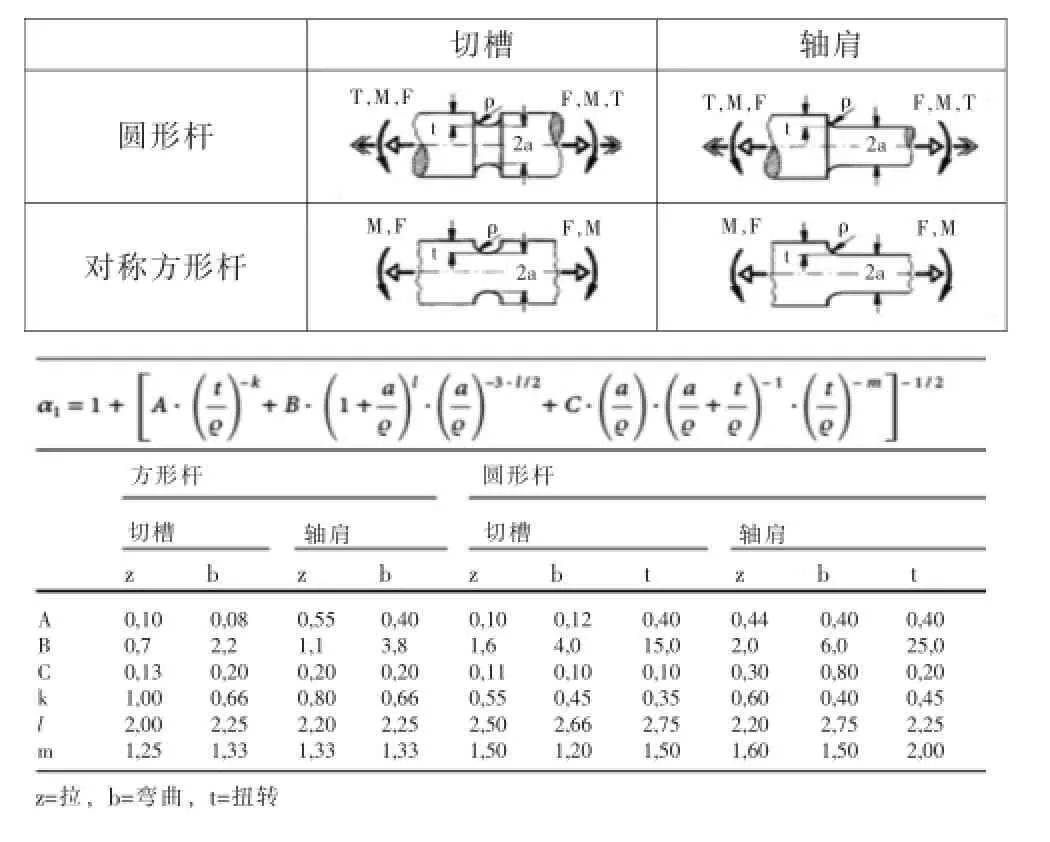
表3　圆形杆和对称方形杆应力集中系数计算近似方程Tab.3 Approximate equation for calculating the stress concentration factor of round and symmetrical square rods

3　计算结果验证及误差分析

为保证Matlab计算结果的正确性，要确保每个子程序计算结果正确。在整个程序中，其他子程序均可通过简单的公式带入来验证计算结果的准确性，但是在计算最大弯矩时用到了 Matlab中的方程极值计算函数fminbnd（f（x），a，b），为了确定这个函数可以准确的计算出合成弯矩方程的极值，我们进行了如下的验证。

如图4所示，一个悬臂梁同时受到了单力、均布和递减载荷的作用发生弯曲，产生弯曲应力。现将其分解为分别单独受到这三种载荷的三个相同的悬臂梁，可得到如下的三个单独弯矩图。

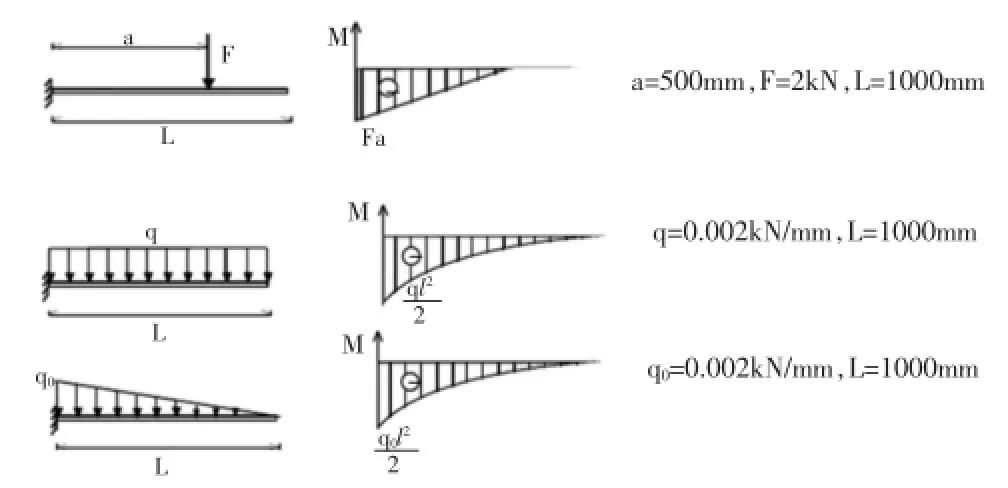
图4　受到线性叠加载荷的悬臂梁线性分解为三个受单一载荷的悬臂梁Fig.4 Linear decomposition of cantilever by linear superposition load in three cantilevers by single loads

根据这三个弯矩图可以看出，悬臂梁受到最大弯矩位置在梁首，即x=0处，最大弯矩的大小为分解后三个梁首所受弯矩之和，即：

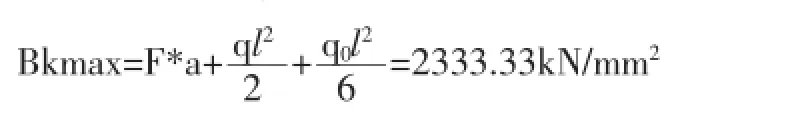
将相同的数据带入Matlab程序中，可得到：

xk=4.5085e-05

Bkmax=2.3333e+03

比较两个计算结果可以看出，Matlab可以准确计算出合成总弯矩方程的极值Bkmax。xk为极值出现的位置，由于Matlab程序本身的计算精度这个值产生了微小的误差，可忽略不计。

其次在用Matlab求应力集中系数时采用了近似方程，而非传统的读取应力集中系数曲线，因此两个结果间存在误差。经大量数据测试，利用近似方程求出的应力集中系数普遍超过曲线中读取结果的10%左右。这说明，当Matlab计算出的构件强度满足强度条件时，在实际工程中这个构件一定满足强度要求不会发生失效。因此，计算应力集中系数而产生的误差使强度得到了更为保守安全的校核结果，是可接受的误差。

4　结论

本文利用胡克定律和强度理论，实现了利用Matlab编程计算具有不同截面的各向同性材料制成的杆件在静态的复合外部载荷下的强度计算。对计算结果进行误差分，确保在适度误差下杆件在实际工程中也不会发生失效，从而保证校核结果的可靠性。通过在Matlab中实现各向同性材料的强度计算，可以在汽车产品设计的早期阶段就对相关构件进行强度校核，保证汽车在足够的强度和安全性能下达到轻量化生产的目标。

［1］宋子康，蔡文安.材料力学［M］.上海同济大学出版社，1997.

［2］同济大学航空航天与力学学院基础力学教学研究部.材料力学［M］.上海同济大学出版社，2011.

［3］Gross，D.；Hauger，W.；Schröder，J.；Wall，W.A.：Technische Mechanik 1.Statik.10.Auflg.Berlin，Heidelberg：Springer-Verlag，2011.

［4］Haibach，E.：Betriebsfestigkeit-Verfahren und Daten zur Bauteilberechnung.3.Auflg.Berlin，Heidelberg：Springer-Verlag，2006.

Strength Calculation of Isotropic Materials with Matlab

LI Xin，SHEN Bin
（Sino-German Kollege，Tongji University Shanghai，Shanghai 201804，China）

In order to realize the efficient and fast analysis of the properties of various materials in carrosserie，it is of realistic significance to take use of Matlab to assess the material properties.This article describes the methods of strength calculation，when the rods with different cross-sections，which are made of isotropic materials，are subjected to multiple linear superposition of external static load.Besides，the effects of stress concentration are also discussed in this article.What's more，the main ideas of the algorithm，which are used to implement the strength calculation of isotropic materials with Matlab，are presented after the theoretical basis.Finally，to ensure the reliability of the results，the results from Software and practical calculation are compared and the errors are analyzed.The implementation of this algorithm proves that the security of vehicles can be ensured during the realization of lightweight production.

isotropic；strength calculation；Matlab programming

TQ9

Adoi：10.3969/j.issn.1002-6673.2015.05.026

1002-6673（2015）05-068-04

2015-07-14

李昕（1989-），陕西人，硕士研究生。研究方向：机械制造及其自动化；沈斌（1955-），上海人，现任同济大学中德学院机械信息技术基金教研室教授、主任、中国自动化学会制造技术专业委员会委员、中国机电一体化应用技术协会理事。研究领域：制造系统与自动化技术、网络化设计与制造及其相关技术、CAD/CAPP/CAM及PDM集成技术、智能制造技术。