基于典型样本的信度函数分配的构造方法

王 霞，田 亮

（华北电力大学控制与计算工程学院，河北保定071003）

基于典型样本的信度函数分配的构造方法

王 霞，田 亮

（华北电力大学控制与计算工程学院，河北保定071003）

D-S证据理论信度函数分配的取值是得到较为准确的融合结果的关键，然而传统方法如采用隶属度函数、正态分布等得到的信度函数分配都具有较大的主观性。为使信度函数分配更具客观性，在总结其它方法的基础上，提出了基于典型样本的信度函数分配构造方法。首先采集各目标模式下的样本，并判断每一模式下的各条证据服从何种概率分布，利用相应的概率公式计算待识别目标模式的各条证据的概率密度，然后进行归一化处理，最后利用联合规则得到融合结果。实例表明利用此法可得到较为准确的融合结果，不仅提高了判别结果的准确性，而且降低了不确定度，并再一次证明了融合诊断结果比单一数据具有更高的可靠性。

证据理论；信度函数；典型样本；概率分布

0 引言

由于D-S证据理论数据融合算法比单一传感器诊断结果可靠，故其在融合诊断和模式识别方面得到了广泛应用［1］。在证据体确定的情况下，由于联合规则是固定的，所以信度函数分配的获取就造成了融合结果的不同。目前信度函数分配的获取大致有以下几种方法:把隶属度函数经适当变换代替专家经验得到基本概率，概念清晰，使用方便，但易受个人经验的影响［2］；采用汉明距离得到信度函数分配，意义明确，较为简单，但目标模式较多时，会产生信息丢失现象［3］；利用正态分布计算证据在各目标模式下的信度密度值，然后进行归一化处理得到信度函数分配，意义明确，减小了对专家经验的依赖，但有时候证据的概率密度并不服从正态分布［4，5］。

本文在总结以上文献中经验的基础上，提出首先对大量历史样本进行分布判断，然后选取相应的概率密度函数计算待判别目标模式的概率密度，然后进行归一化处理得到信度函数分配值，这种方法物理意义明确，与实际的结果相吻合，有效减小了对专家经验的依赖。

1 相关概念

1.1 识别框架

如果定义代表某一事物的参数为θ，可能取值的集合为Θ，则称Θ为识别框架。在故障诊断中，每一种可能的故障都为假设，各种可能故障的集合为识别框架，故障的每一症状为证据。

如果Θ是一个识别框架，那么函数m:2Θ→［0，1］称为基本概率分布，满足:

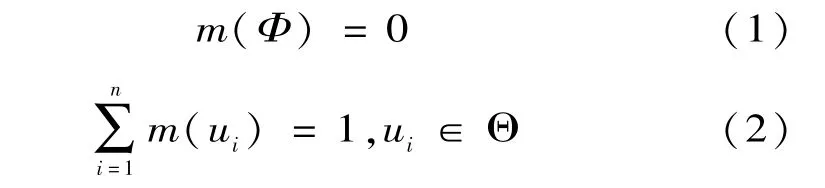
式中:m（ui）表示证据分配到ui上的信度函数值，m（ui）越大，表明该条证据可信度越大；反之则说明该条证据的可信度越小。

1.2 联合规则

根据D-S联合规则，设m1，m2分别为同一识别框架Θ上的2个信度函数分配［6］，焦元分别为:｛u11、u21、…ui1｝，｛u12、u22、…uj2｝，设:

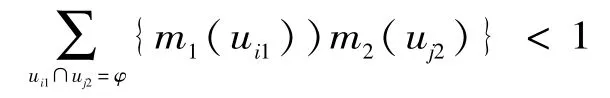
则由下式定义的函数:

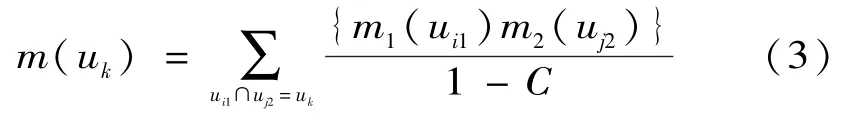
当uk=Ф时，m（uk）=0，式中:i、j、k= 1、2、…n；其中:

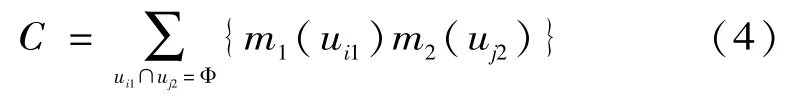
为联合后的信度函数分配。C是表示完全冲突假设ui1和uj2所有信度函数乘积之和，所谓完全冲突是指ui1和uj2在Θ中不可能同时发生。对于D-S证据理论，其结果不受证据组合次序先后的影响，但在证据较多时，可先将证据两两融合，尽量避免使用中间融合结果，提高计算的精度和准确率。

1.3 融合结果判定规则

尽管有很多不同的案例，但是对于目标模式的判定具有相似的基本规则:

（1）因为信度函数分配代表了可信度的大小，显然信度函数分配值最大的目标模式可作为最终的判定结果。

（2）为了较少模棱两可的情况出现，判定的目标模式和其它任一目标模式信度函数分配值之差应大于某个限值，此限值依具体情况而定。

（3）整个目标系统的不确定度必须小于某个限值［2］，以提高判别结果的可靠性。

2 信度函数分配的获取方法

2.1 典型样本

设待识别的目标模式为｛u1，u2，u3，…，un｝，对任一目标模式存在m个相互独立的特征变量对其进行描述，设为｛x1j，x2j，x3j，…xmj｝，j∈m，即为待融合的目标模式。所有目标模式下的各证据的典型值为｛x′1j，x′2j，…，x′mj｝，称为典型样本。

在实际生产中，由于历史数据较多，难以确定典型样本，任一目标模式下的特征变量的取值可以是某一区间内的任一值。某一样本出现的次数越多，其发生的概率越大，因此可以将概率密度值最大的样本作为典型样本。

2.2 概率密度函数

各目标模式下的特征变量是一个随机变量，本文将探讨的变压器故障诊断的实例中，特征变量是一个非负实数，且取值具有一定的概率密度f（x）。f（x）与置信概率p之间存在如下关系:

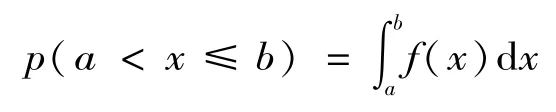
各目标模式下的证据分布可能相同或不同，至于服从何种分布可以利用MATLAB程序对样本进行判断。通常情况下，样本量越大，对概率分布的判断就越准确。整理文献［7］附录提供的数据并进行概率分布判断，得出其均服从对数正态分布。而对数正态分布的概率密度函数f（x）为

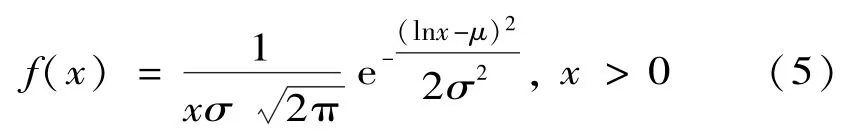
对数分布的概率密度y与随机变量x的函数图像如图1所示。

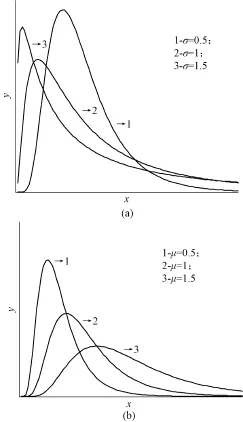
图1 对数分布的概率密度函数

图1（a）所示的是μ相同而σ不同时对数分布的概率密度函数的图形。

图1（b）是σ相同而μ不同时对数分布的概率密度函数的图形。

由对数分布的概率密度函数公式和图形可以得出以下结论；

（1）f（x）取最大值时的x值为

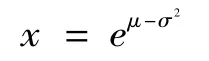
而此时的概率密度值为:

（2）μ相同时，σ越小，f（x）的极大值点越大；σ相同时，μ越大，f（x）的极大值点越大。

图2是置信概率p与x之间的关系。

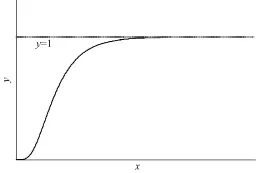
图2 对数分布的累加函数

因此可将f（xij）定义为证据xi在模式uj下的信度密度函数。而对数分布置信区间的构造可采用P值方法［8］，置信度为1-α的置信区间为:

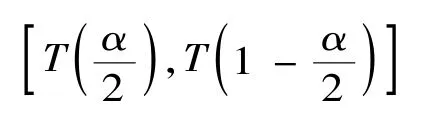
具体计算方法为:

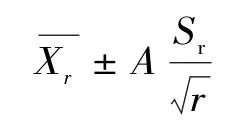
式中:第一项是样本的均值；Sr是样本的标准差；r是样本个数；A可根据α和r的大小查T分布表得到。

从图1可以看出μ越小，概率密度越集中；σ越大，概率密度的极大值点越小，说明引入置信区间的必要性。

在置信区间改变后，概率密度函数的定义域也随之改变，此时的概率密度分布函数记为M（xij），并将其定义为证据xi在目标模式uj下的信度密度函数。

2.3 信度函数分配的构造

引入信度密度函数的目的就是构造信度函数分配。任一条证据xi对应n个信度密度函数值，记为:｛M（xi1），M（xi2），…，M（xin）｝，将不确定的信度密度值定义为n个信度密度函数的标准差［9］，即:

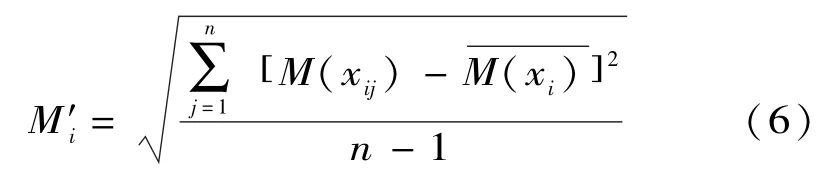
其中:

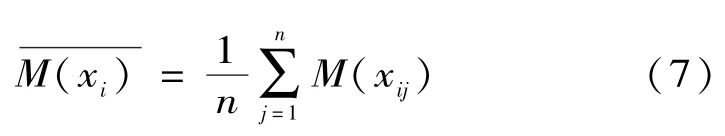
对各信度密度值进行归一化处理，n+1个信度密度值之和为:

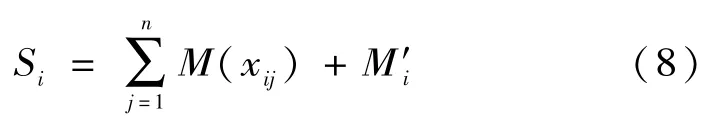
定义证据xi在目标模式uj下的信度函数分配为:

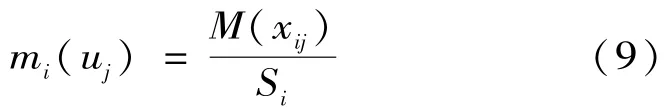
而证据xi在整个目标系统下的不确定的信度函数分配为:

经过验证，上述对信度函数分配的定义满足其定义，在已知样本的情况下就可利用下一节提到的数据处理方法得到各信度函数分配值。

3 数据处理

面对大量的历史数据，需要对其进行处理才能得到每一条证据在各目标模式下的μ和σ这两个参数值。文献［10］中给出了这两个参数的估计方法，其中最常用的是最大似然估计法。设总体X服从参数为μ和σ2的对数分布，X1，X2，…，Xn为来自X的随机样本，那么μ和σ2的最大似然估计量为:

4 实例分析

变压器是发电厂的重要设备，一旦发生故障则需尽快查出故障原因，进行维修，将损失减小到最低程度。然而，变压器结构较复杂，难以根据表面现象判断故障原因。目前最常用的方法就是根据变压器油中提取的5种气体的含量信息进行融合诊断。这5种气体分别为:H2，CH4，C2H6，C2H4，C2H2。因此，可将这5种气体作为证据，而根据变压器最常见的故障类型将识别框架定义为:Θ=｛T1，T2，T3，D1，D2，PD｝，此识别框架的基元分别代表:低温过热、中温过热，高温过热、低能放电、高能放电、局部放电［11］。

根据文献［7］提供的电力变压器DGA数据，应用以上数据处理方法，得到数据样本的参数，如表1所示。

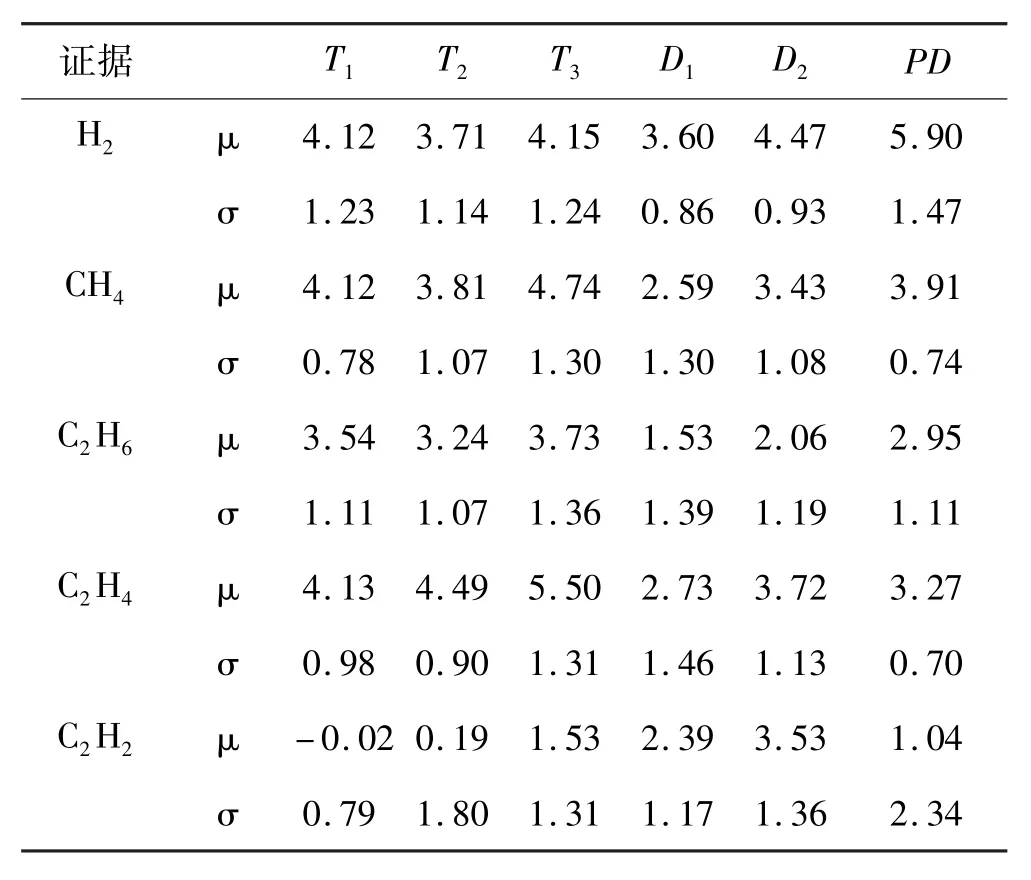
表1 数据样本的平均值及标准差

如某电厂变压器油中检测到的5种特征气体（H2、CH4、C2H6、C2H4、C2H2）含量分别为: 35.61，97.25，21.46，152.47，0.9，单位为μL/L，将上述信度函数分配的构造方法对数据进行处理，可得到每条证据在识别框架下的信度密度值M（xij），在表格中简单记为Mi，将其列于表2中。

在得到各信度密度值之后应用上述提出的信度函数分配构造方法及联合规则得到的中间结果和最终结果列于表3中。信度函数分配mi（uj）在表格中简单记为mi，表中“融合12”代表第1、2种气体信度函数的融合结果，以此类推。

由融合诊断结果可知，变压器的故障类型为高温过热，与文献［7］提供的诊断结果一致，并且降低了不确定度，说明了该方法的有效性。

日本的月冈、大江等人［12］提出当热点温度高于400℃时，估算热点温度的经验公式为:

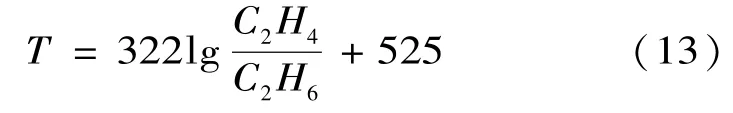
计算得出热点温度为799℃。

当故障点或故障部分的温度处于600～800℃之间时，故障多为铁芯多点接地［12］。故障点具体位置的查找目前多采用电气测试法。

由表3中的计算结果可知，随着证据的加入，某一模式的融合结果逐渐增大并成为最终融合结果中的最大值，再一次说明了融合诊断结果比单一诊断结果的可靠性要高。

5 结论

提出了一种基于D-S证据理论的信度函数分配的构造方法，并将其应用于变压器故障诊断中。通过中间融合结果和最终融合结果的比较可知，当证据越多时，计算结果越可靠，但会增加计算量。为了得到较为精确的结果，应尽量使用原始数据，减少中间结果的使用次数。

［1］ 潘泉，程咏梅，梁彦，等.多源信息融合理论及应用［M］.北京:清华大学出版社，2013.

［2］ 朱大奇，于盛林.基于D-S证据理论的数据融合算法及其在电路故障诊断中的应用［J］.电子学报，2002，30（2）:221-223.

［3］ 田亮，常太华，曾德良，等.基于典型样本数据融合方法的锅炉制粉系统故障诊断［J］.热能动力工程，2005，20（2）:163-166.

［4］ 杨静，田亮，赵爱军，等.基于典型样本的证据理论信度函数分配构造方法［J］.华北电力大学学报，2008，35（5）:70-72，77.

［5］ 赵亮宇，田亮，王琪，等.基于改进信度函数分配方法的煤种判别技术［J］.华北电力大学学报，2011，38（4）:71-75.

［6］ 齐政，杨以涵，张宏宇.基于D-S证据理论的小电流接地故障连续选线方法［J］.华北电力大学学报，2005，32（3）:1-4.

［7］ 尹金良.基于相关向量机的油浸式电力变压器故障诊断方法研究［D］.北京:华北电力大学，2013.

［8］ 张志国.小样本条件下对数正态分布均值置信区间［J］.齐齐哈尔大学学报（自然科学版），2008，24（4）:75-78.

［9］ 吴石林，张玘.误差分析与数据处理［M］.北京:清华大学出版社，2010.

［10］ 于洋.对数正态分布的几个性质及其参数估计［J］.廊坊师范学院学报（自然科学版），2011，11（5）: 8-11.

［11］ 张利伟，苑津沙.基于典型样本和证据理论的变压器故障诊断［J］.电测与仪表，2013，（8）:14-19.

［12］ 丁军.大型变压器铁芯多点接地的处理探讨［C］.//第四届安徽科技论坛安徽省电机工程学会分论坛论文集.马鞍山电机工程学会，2006:397-411.

Method of Constructing Confidence Function Distribution Based on Typical Sample

Wang Xia，Tian Liang
（School of Control and Computer Engineering，North China Electric Power University，Baoding 071003，China）

The value of D-S evidence theory of belief function assignment is the key to get accurate fusion results，while traditional methods，such as the belief function assignment got through the usage of the membership function and the normal distribution，tend to be more subjective.In order to make the belief function assignment more objective.This paper puts forward a method constructing belief function assignment after combining other methods and analyzing the typical samples.First，samples were collected for each target mode，and which probability distributions the evidence of each mode obeys was judged.Then，the probability density of each piece of evidence was calculated by using corresponding probability formula.Finally，normalized processing was carried on，and the union rule was used to obtain the fusion results.The example shows that using this method can get more accurate results of fusion，and this method can not only improves the accuracy of the result of discrimination，but also reduce the uncertainty.In addition，it proves that the fusion diagnosis has a higher reliability than a single data.

evidence theory；typical sample；probability density；belief function

TK223

A DOI:10.3969/j.issn.1672-0792.2015.05.003

2015-03-26。

国家重点基础研究发展计划（973计划）（2012CB215203）；中央高校基本科研业务费专项资金（2014MS145）。

王霞（1990-），女，硕士研究生，研究方向为数据挖掘与信息融合，E-mail:1016228976@qq.com。