垂直微结构剖面仪主体结构优化

姜　欣　刘玉红　宋诗军　王延辉

天津大学，天津，300072

垂直微结构剖面仪主体结构优化

姜欣刘玉红宋诗军王延辉

天津大学，天津，300072

垂直微结构剖面仪是获取海洋微结构湍流数据最有效的测量平台，其下降过程中产生的流致振动是影响剖面仪测量精度的主要因素。分析了影响剖面仪流致振动的因素，基于ANSYS-Workbench数值仿真平台，采用双向流固耦合算法，得到了剖面仪流致振动与其结构外形及参数之间的关系。在此基础上，以减小流致振动为目标，采用单目标优化方法分别对剖面仪主体结构外形及结构参数进行了优化，优化后的剖面仪测量精度提高了57%。研究成果为垂直微结构剖面仪及类似结构的合理设计提供了理论指导。

垂直微结构剖面仪；测量精度；流致振动；流固耦合；结构优化

0　引言

海洋微结构湍流对海水的动量、热量和质量输运都有重要贡献，对海水运动速度、温盐特性及水中溶解态、颗粒态物质的分布有显著影响[1]，是产生海洋宏观现象的原动力。搭载翼型剪切流传感器的垂直微结构剖面仪是精确测量海洋微结构湍流数据的最有效和普遍的测量平台。

垂直微结构剖面仪(以下简称剖面仪)的研制始于20世纪70年代，由Osborn[2]研制成功，并搭载了翼型剪切流传感器，成功地对海洋微结构湍流进行了测量。目前，加拿大、美国、日本及欧洲部分国家对剖面仪的研制处于领先水平[3-8]。国内仅天津大学最早于2004年开始进行剖面仪的研制[9]，历经原理样机、试验样机，于2011年研制成功我国第一台剖面仪工程样机[10-11]。目前剖面仪不仅可以测量海洋微结构湍流，而且可以搭载CTD、浊度计等进行海洋温度、盐度、浊度等海洋环境参数的测量。

剖面仪下降过程中产生的流致振动是影响其测量精度的主要因素。流致振动现象是剖面仪下降过程中不可避免的一种有害现象，会影响剖面仪的运动稳定性，从而影响湍流测量数据的准确性。为了减小剖面仪下降过程中产生的流致振动影响，本文以天津大学研制的第二代剖面仪工程样机为对象，分析影响剖面仪流致振动的结构因素，以减小流致振动为目标，对剖面仪外形及结构参数进行优化设计。

1　剖面仪的流致振动及计算方法

1.1剖面仪的流致振动

剖面仪在下降过程中受到流体力的作用，会改变剖面仪的运动状态，剖面仪运动状态的改变反过来又会影响剖面仪周围的流场，从而使剖面仪受到的流体力发生改变。剖面仪与流体的相互作用最终会达到稳定，使剖面仪呈现出规律的摆动，这就是剖面仪的流致振动。

Moum等[8]对Chameleon剖面仪的实验数据进行分析后指出，流致振动决定着剖面仪湍动能耗散率的测量下限。Osborn[2]在使用第一台垂直剖面仪测量时发现，低频率的剪切流数据不是实际的流速脉动，而是剖面仪本体由于流致振动而产生的低频钟摆运动。Miller等[12]在AMP系列剖面仪研究过程中发现，当剖面仪的流致振动频率接近固有频率时会引起剖面仪的共振，严重影响剖面仪的测量精度，他还指出平滑的剖面仪壳体(如减少凸起)可改善剖面仪的流致振动情况。以上研究结果表明，剖面仪的流致振动与其结构密切相关，因此，可通过优化剖面仪的结构形状及结构参数来降低剖面仪的流致振动效应。

1.2流致振动计算方法

基于ANSYS-Workbench数值仿真平台，将流体计算软件CFX与结构计算软件ANSYS结合进行流固双向耦合计算，由CFX进行流场计算，ANSYS进行结构计算。采用双向分离式顺序计算方法，即流固耦合系统的流体域和固体域按各自划分的网格与设定的参数分别进行计算，然后在流固耦合面上进行计算数据的传输，实现耦合计算，其中CFX向ANSYS传输的是剖面仪的受力情况，ANSYS向CFX传输的是剖面仪的位移情况。文献[13]证明了利用该方法进行剖面仪流致振动计算的准确性与可靠性。

流固耦合计算区域计算区域为长方体，如图1所示。为保证流体充分发展，剖面仪前端距流体入口的距离L1=2L，剖面仪后端距流体出口的距离L2=3L，其中L为剖面仪主体长度(图1中点A、O之间距离)；由于剖面仪流致振动的计算涉及动网格，剖面仪在横向进行摆动，所以水域的宽度W要取得足够大，在此取H=W=16D，其中D为剖面仪的直径。图1中O点为摆动中心的位置，Fx为剖面仪浮心的位置，Gx为剖面仪重心的位置，A点为观测点。计算时，记录观测点A的位移与速度，从而获得剖面仪的流致振动数据。

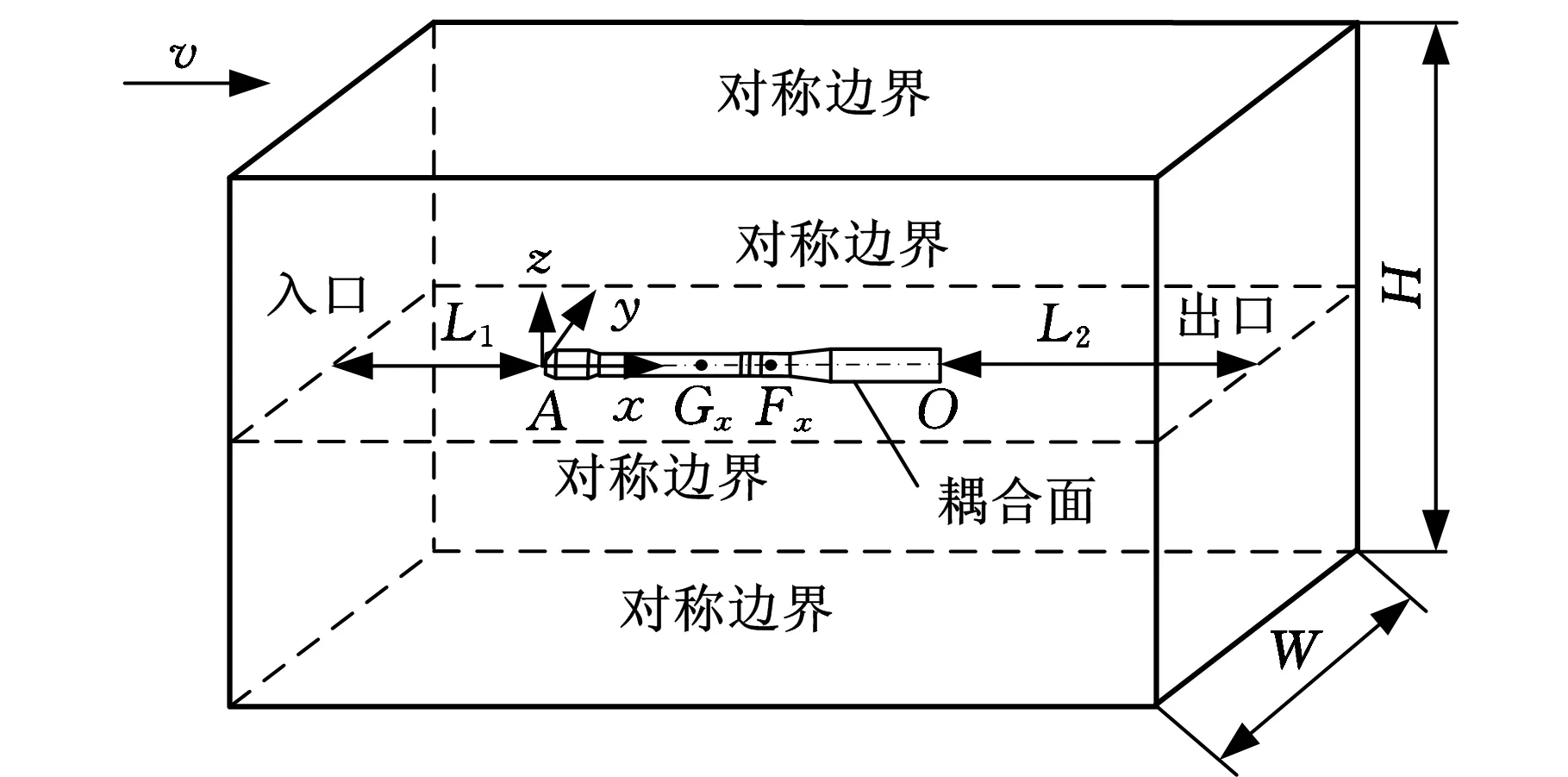
图1　剖面仪计算区域示意图

流体区域与结构区域均采用四面体进行网格划分。为了保证计算精度，经网格独立性检验，流场区域剖面仪最大面网格设为16 mm，增长率设为1.1，结构区域剖面仪面网格最大尺寸为30 mm。

流体区域的入口设为速度入口，流速取剖面仪实际工作速度0.65 m/s，流体区域出口设为压力出口，流体四周的区域边界设为对称边界条件，剖面仪的壁面设置为流固耦合面。流场计算采用k-ε湍流模型，时间歩长为0.1 s，总计算时间为80 s。计算时，记录观测点A处的速度及位移变化曲线。

2　剖面仪结构外形优化

最初Osborn[2]的垂直剖面仪采用的是圆球状，但在海试试验中发现圆球状的剖面仪在下降过程中会产生较大的旋转和振动，从而产生较大的测量误差。经过诸多研究者的不断研究、试验与改进，发现长圆柱体的外形相较于其他形状具有更好的下降稳定性，而且下降过程中不易倾斜和偏转，所以如今的剖面仪均采用长圆柱的主体外形。虽然整体的形状可以确定为长圆柱形，但局部形状的不同也会导致流致振动的不同。因此，本文针对天津大学研制的第二代长圆柱体形剖面仪，对其局部结构(头部及主体)形状进行优化。

2.1头部形状优化

天津大学研制的第二代剖面仪的原始头部端面设计为一平面，如图2a所示，这种结构易使剖面仪下降过程中在头部流场产生边界层分离，从而增大流致振动效应。为改善头部流场情况，将剖面仪头部设计为半椭球形，如图2b所示，可以减小头部末端的边界层分离。为优化头部椭球形状，令椭球头部轴线方向尺寸L在60～120 mm之间变化，径向尺寸保持不变(为剖面仪主体直径尺寸160 mm)，分别建立模型进行流致振动计算。计算结果如图3所示。

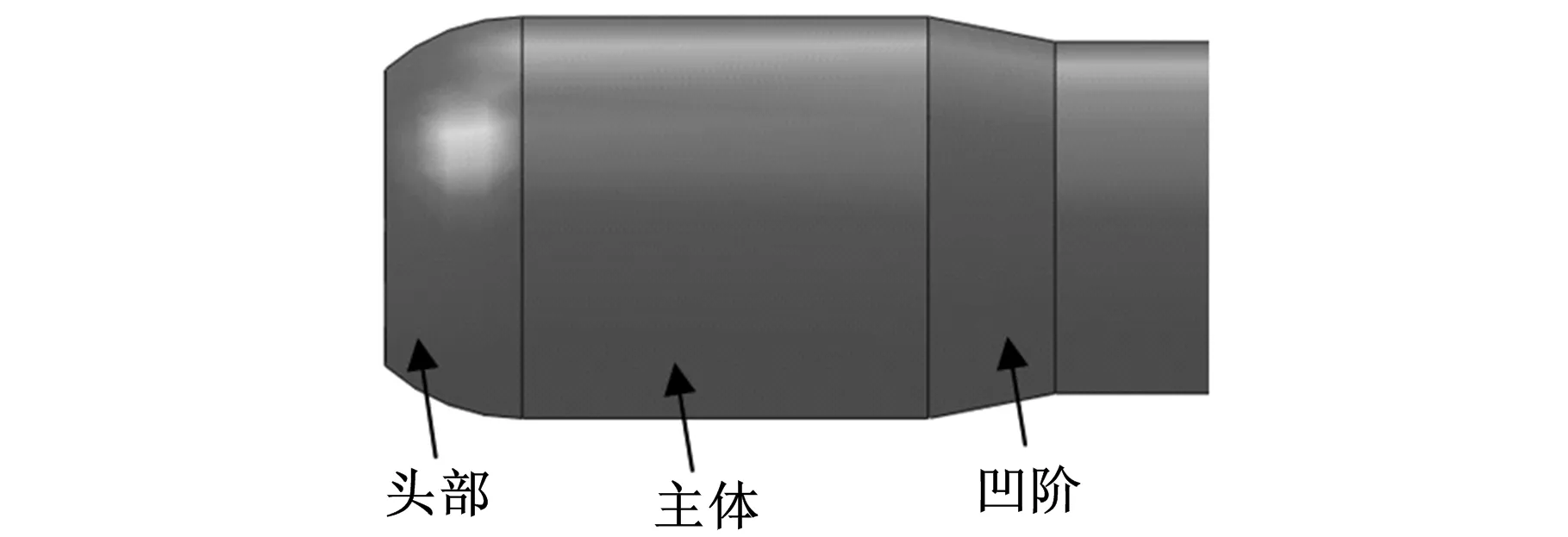
(a)原始头部形状

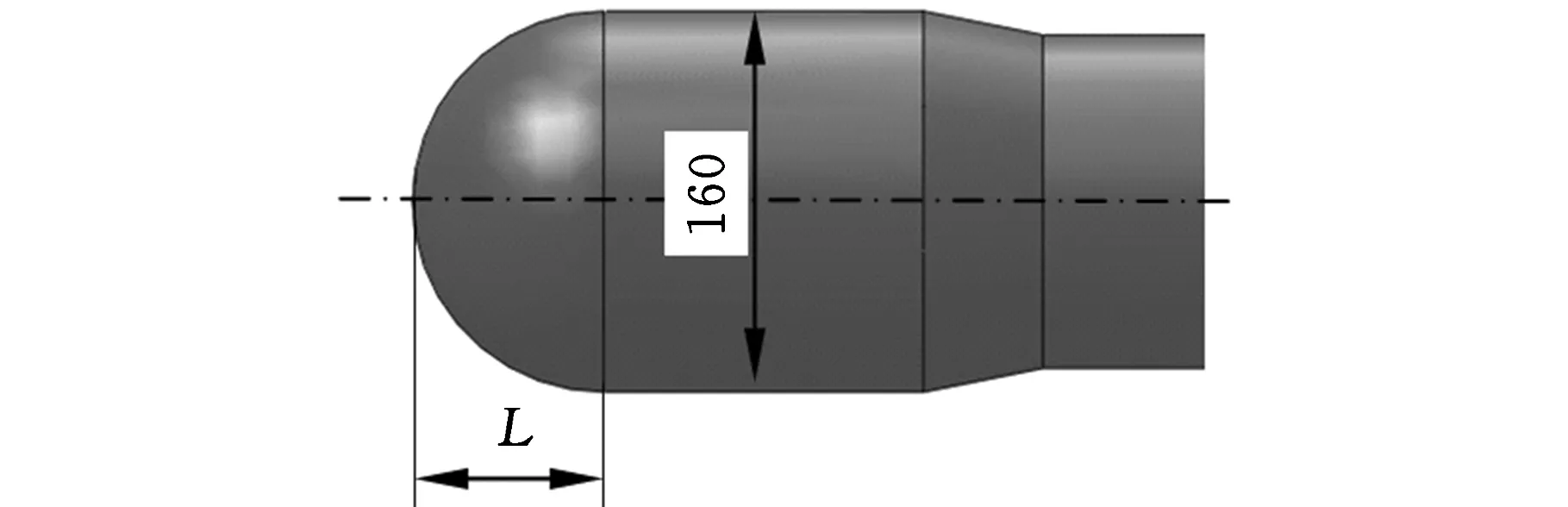
(b)椭球形头部图2　剖面仪头部形状

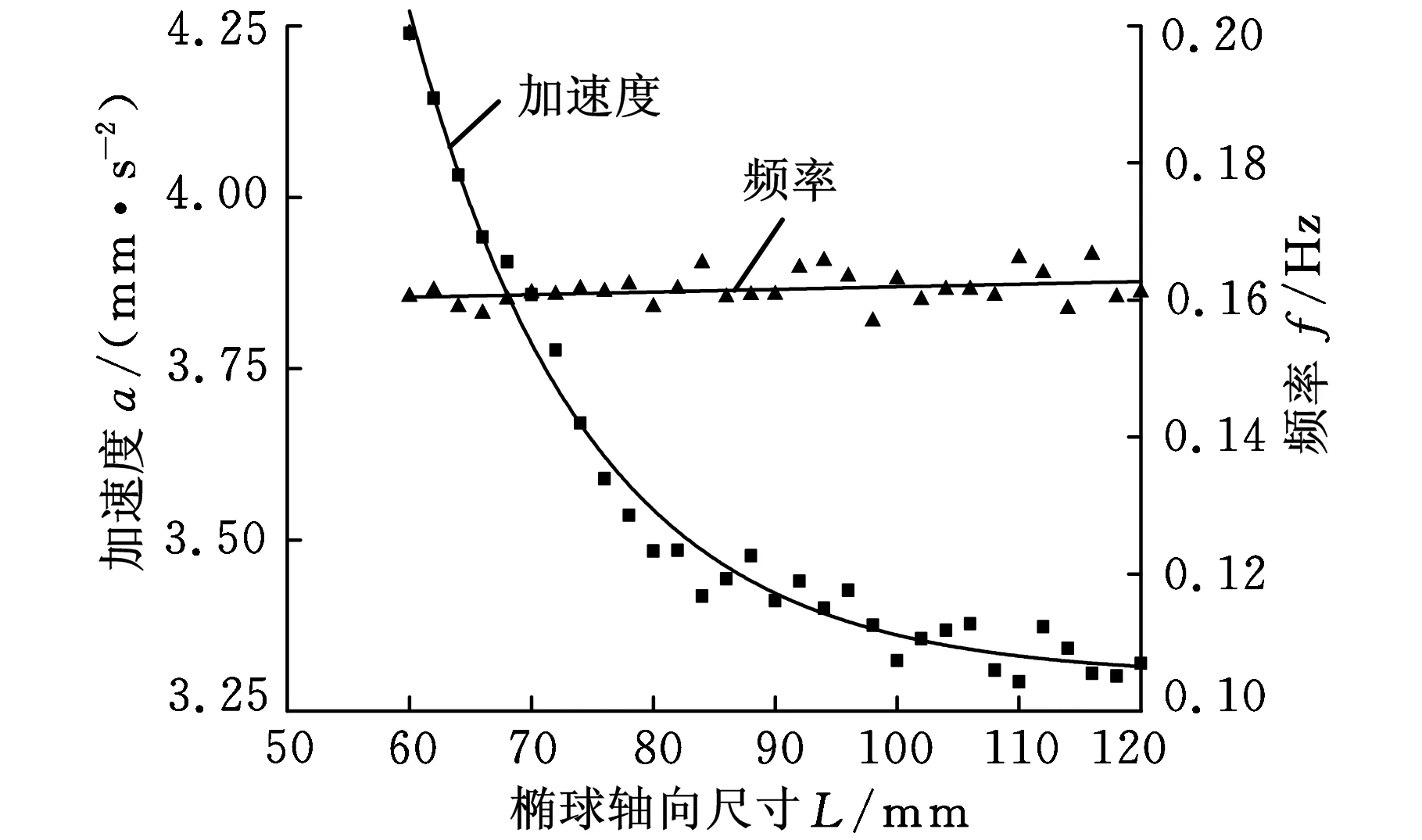
图3　剖面仪头部椭球轴向尺寸对流致振动的影响

图3中，左侧纵轴为剖面仪前端监测点A的y向加速度，右侧纵轴为剖面仪流致振动频率。由图3知，剖面仪头部形状尺寸对流致振动的频率影响很小，频率在0.16 Hz左右变化；椭球体头部轴向尺寸的增大会使流致振动的加速度幅值减小，两者近似成指数关系；当轴向尺寸大于80 mm(即半球形)时，随着尺寸的增大，流致振动的减小幅度较小、程度变缓。同时考虑到安装传感器的需求，剖面仪头部前端曲率不能过大，因此剖面仪前端设计成半球形较为合适。

2.2主体结构外形优化

原始设计中，剖面仪前端具有凹阶结构，如图2所示。研究发现，剖面仪下降时在凹阶处会发生边界层分离现象，如图4所示。由图4可以看出，凹阶处发生了涡的脱落，并且脱落的涡又会在后部再次附着，造成后面涡结构的混乱，导致流致振动程度的增强。因此，对有无凹阶结构的剖面仪进行流致振动对比计算，得到加速度的幅值和振动频率，见表1。由表1可以看出，去掉凹阶结构使剖面仪的流致振动加速度幅值减小了31.17%，明显减缓流致振动幅度，因此在设计中应尽量避免凹阶结构的出现。

图4　凹阶处涡脱落图

主体外形加速度幅值(mm/s2)频率(Hz)无凹阶2.650.147有凹阶3.850.142

3　剖面仪结构参数优化

由上文分析知，剖面仪的最优外形结构如图5所示，头部为半球形，主体为长圆柱，而且无凹阶结构。除外形影响流致振动外，剖面仪的结构参数(如长径比和重浮心距离)对流致振动也具有重要影响，同样需要优化以减小剖面仪的流致振动。

图5　剖面仪主体外形示意图

3.1长径比

按图5所示外形建立流固耦合计算模型。设计时，当剖面仪质量确定后，剖面仪的体积也为一定值，因此，计算中改变长径比时应保证体积不变。令剖面仪长度L分别为1.7～2.1m，对应算出剖面仪的直径D，从而得到剖面仪的长径比L/D。图6所示为监测点A的y向加速度和振动频率随长径比的变化曲线。由图6知，随着长径比的增大，流致振动的频率越来越低；剖面仪的振动加速度幅值与长径比成非线性关系，随着长径比的增大，剖面仪流致振动幅值越来越小。

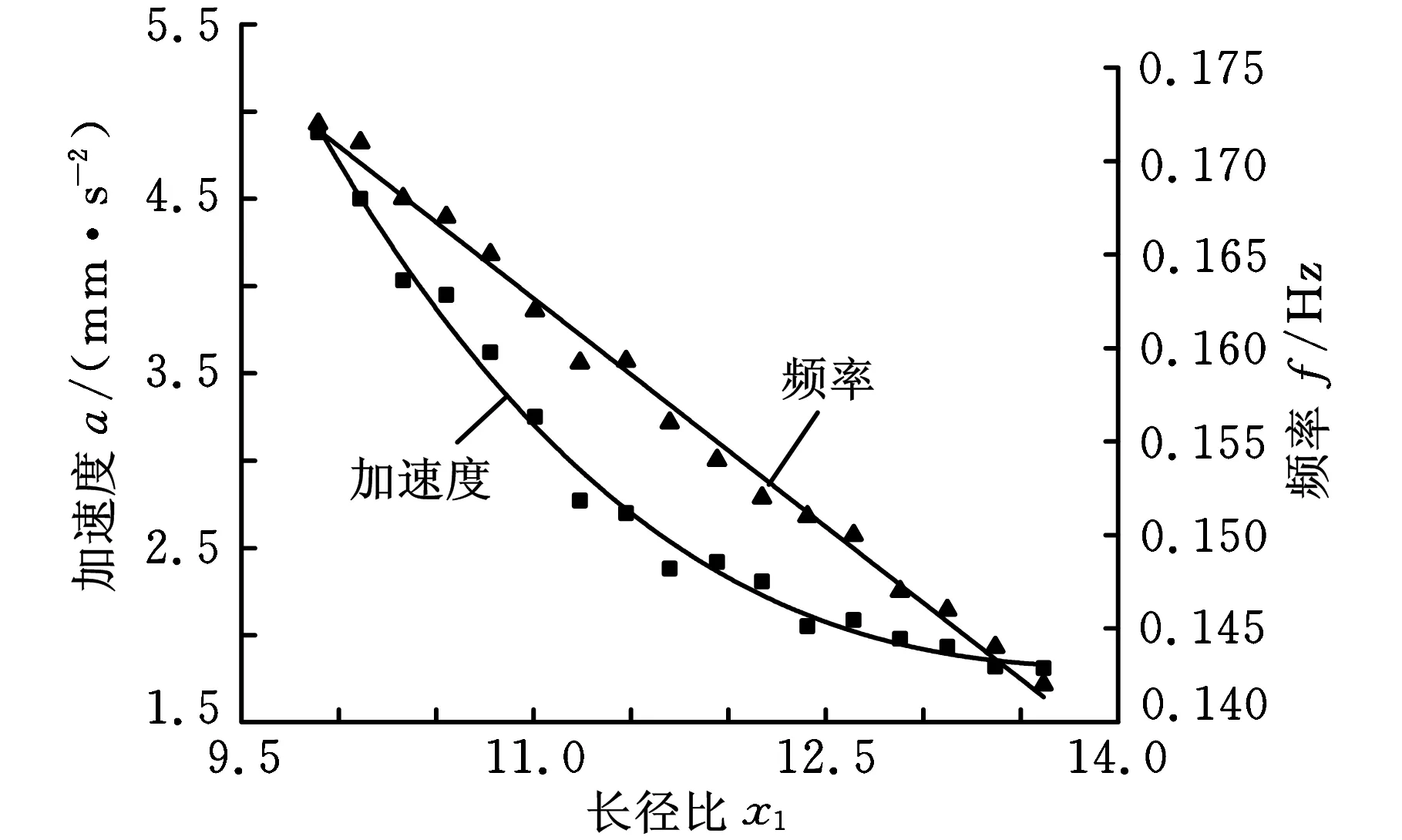
图6　长径比对流致振动的影响

根据计算结果，流致振动的频率f与长径比成线性关系，其关系式可表述为

f=-8.14×10-4x1+0.2522

(1)

其中，x1代表剖面仪的长径比。振动加速度幅值a随长径比的变化按三次多项式进行似合，其关系式为

(2)

拟合关系式的R平方值为0.9896，说明拟合公式可信。

剖面仪下降过程中，要求振动的幅值越小越好，而且振动频率应远离剖面仪的固有频率，因此，优化模型中选取振动加速为优化目标，以剖面仪的固有频率为约束条件。优化模型的目标函数为

min(a)10≤x1≤13.5

(3)

由微结构流速剪切信号的调理方法知，剖面仪测量湍流动能耗散率的估计值可表示为[14]

(4)

式中，fm为微结构流速剪切信号的频率。

由于剖面仪的共振频率决定了能够测量的信号最大频率，故当剖面仪测量上限大于10-5W/kg时，由式(4)求得剖面仪的一阶固有频率应大于115.6Hz。因此，优化模型的约束条件定义为

fL≥115.6Hz

(5)

求解式(3)和式(5)组成的优化模型，得到长径比的最优解为12。

3.2重浮心距离

计算时保持模型形状不变，因此浮心位置不变，改变重心位置，使重浮心距离在150～450mm之间变化。图7所示为剖面仪流致振动加速度和振动频率随重浮心距离的变化曲线。由图7可看出，重浮心距离与剖面仪流致振动频率成正比关系，其关系式可表述为

f=0.376x2+0.0365

(6)

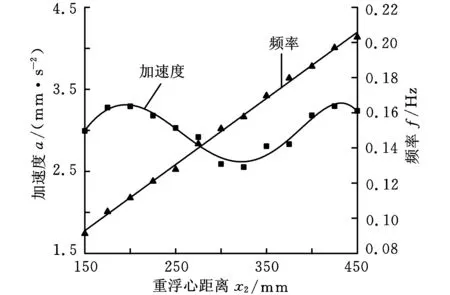
图7　重浮心距离对流致振动的影响

其中，x2代表重浮心距离。而流致振动加速度幅值随重浮心距离的变化则较为复杂。本文采用五次多项式进行拟合。五次多项式拟合流致振动加速度与剖面仪重浮心距离的关系式为

(7)

拟合关系式的R平方值为0.9359，说明拟合公式可用。

实际中重浮心距离变化的范围为200～400mm。仍然以剖面仪流致振动的加速度幅值最小作为优化目标，以剖面仪的固有频率作为约束条件，建立优化目标模型。目标函数为

min(a)200mm≤x2≤400mm

(8)

约束条件为式(5)。联立式(8)和式(5)，得到重浮心距离的最优解为322 mm。

4　优化效果分析

优化后的剖面仪结构外形及相关尺寸如下：剖面仪头部形状为半球形，主体为长圆柱体，无凹阶结构，长径比为12，重浮心距离为322 mm。优化前剖面仪结构外形及相关尺寸如下：剖面仪头部形状为平面，主体为长圆柱体，有凹阶结构(图2a)，长径比为11，重浮心距离为360 mm。分别对优化前后的剖面仪进行流致振动计算，得到优化前后剖面仪流致振动加速度幅值分别为3.85 mm/s2和2.52 mm/s2。

剖面仪的测量精度主要指剖面仪对海洋湍流动能耗散率的测量范围，即测量下限和测量上限。其中剖面仪测量上限主要由其搭载的剪切流传感器决定，而测量下限则主要由剖面仪的流致振动决定。为验证结构优化后剖面仪测量精度改善情况，可对结构改进前后剖面仪的测量下限进行比较。剖面仪的测量下限估算公式[14]为

(9)

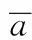
5　结论

(1)具有流线形头部的剖面仪比具有平面形头部的剖面仪在下降过程中产生的流致振动强度弱；并且剖面仪外表面有凹阶时，会加剧流致振动的强度。

(2)对于具有椭球体流线形头部的剖面仪，当剖面仪主体径向尺寸一定时，剖面仪头部轴向尺寸对流致振动的影响较小，但对流致振动加速度的振幅影响较大，两者近视成指数关系递减。

(3)剖面仪流致振动频率随剖面仪长径比的增大呈线性减小的趋势，而流致振动加速幅值则随剖面仪长径比的增大呈幂指函数减小的趋势。

(4)剖面仪流致振动频率随剖面仪重浮心距离的增大呈线性增大的趋势，而流致振动加速幅值与剖面仪重浮心距离的关系则较为复杂，未呈现简单的升与降关系。

(5)结构优化后的剖面仪流致振动强度有所减弱，使剖面仪的测量精度提高了57%。

[1]魏皓,武建平, 张平. 海洋湍流模式应用研究[J].青岛海洋大学学报, 2001, 31(1):7-13.

Wei Hao, Wu Jianping, Zhang Ping. Review on Turbulence Closure Models in Ocean Hydrodynamics[J]. Journal of Ocean University of Qingdao,2001, 31(1):7-13.

[2]Osborn T R.Vertical Profiling of Velocity Microstructure[J]. Journal of Physical Oceanography, 1974, 4: 109-115.

[3]Polzin K L, Montgomery E T. Microstructure Profiling with the High Resolution Profiler[C]//Proceedings of Microstructure Sensor Workshop.Massachusetts,1996：1-16.

[4]Prandke H. Microstructure Profiler to Study Mixing and Turbulent Transport Processes[C]//Oceans’98 Conference Proceedings.Nice,1998:179-183.

[5]Schmitt R W, Toole J M, Koehler R L. The Development of a Fine and Microstructure Profiler[J]. Journal of Atmospheric and Ocean Technology,1988,5(4):484-500.

[6]Wolk F, Yamazaki H, Seuront L, et al. A New Free-fall Profiler for Measuring Biophysical Microstructure[J]. Journal of Atmospheric and Ocean Technology, 2002, 19(5): 780-793.

[7]Lueck R G,Wolk F, Yamazaki H. Oceanic Velocity Microstructure Measurements in the 20th Century[J]. Journal of Oceanography,2002,58:153-174.

[8]Moum J N, Gregg M C, Lien R C,et al. Comparison of Turbulence Kinetic Energy Dissipation Rate Estimates from Two Ocean Microstructure Profilers[J]. Journal of Atmospheric and Ocean Technology,1995,12:346-366.

[9]张大涛, 王延辉, 王树新. 湍流剖面仪系统动力学分析与实验研究[J].海洋技术, 2006, 25(1): 38-42.

Zhang Datao, Wang Yanhui, Wang Shuxin. Dynamics Analysis and Experiment Research for Shear Profiler[J].Ocean Technology,2006, 25(1): 38-42.

[10]王子龙, 王延辉, 陈宝阔, 等. 海洋微结构湍流垂直剖面仪设计与试验[J].天津大学学报，2012, 45(3): 279-284.

Wang Zhilong, Wang Yanhui, Chen Baokuo, et al. Design and Application of Ocean Microstructure Turbulence Vertical Profiler[J]. Journal of Tianjin University,2012, 45(3): 279-284.

[11]兰世泉, 刘玉红, 王延辉, 等. 垂直微结构湍流剖面仪振动源及减振方法分析[J].振动与冲击, 2012, 31(18): 5-9.

Lan Shiquan, Liu Yuhong, Wang Yanhui, et al. Vibration Source Analysis and Vibration Reduction for a Vertical Microstructure Turbulence Profiler[J]. Journal of Vibration and Shock,2012, 31(18): 5-9.

[12]Miller J B, Gregg M C, MillerV W.Vibration of Tethered Microstructure Profilers[J].Journal of Atmospheric and Oceanic Technology, 1989, 6(6): 980-984.

[13]Liu Yuhong, Lan Shiquan, Wang Yanhui,et al. A Numerical Method for Calculating the Flow-induced Vibration of the Microstructure Profiler[C]//Oceans’12 MTS/IEEE.Virginia Beach,2012: 1-5.

[14]Prandke H,Stips A. Test Measurements with an Operational Microstructure-turbulence Profiler: Detection Limit of Dissipation Rates[J]. Aquatic Sciences, 1998, 60: 191-209.

(编辑陈勇)

Structure Optimization for Main Body of Vertical Microstructure Profiler

Jiang XinLiu YuhongSong ShijunWang Yanhui

Tianjin University,Tianjin,300072

Vertical microstructure profiler (VMP) is a most common and effective platform to obtain data of microstructure turbulence in the ocean. The FIV is the main factor affecting the measurement precision of the VMP. Factors influencing the FIV of the VMP were analyzed herein. Based on the numerical simulation platform of ANSYS-Workbench, the FIV of the VMP with various shapes and structure parameters was calculated using algorithm of two-way fluid-structure coupling. Aimed to decrease the FIV, the main body shape and the structure parameters of the main body were optimized respectively. The measurement precision of the optimized profiler is improved by 57%. The present investigation provides scientific guidance for designing the VMP.

vertical microstructure profiler(VMP); measurement precision; flow-induced vibration(FIV); fluid-structure coupling; structure optimization

2013-03-21

国家高技术研究发展计划(863计划)资助项目(2010AA09Z102)；国家自然科学基金资助项目(51105268)

TH113DOI：10.3969/j.issn.1004-132X.2015.01.017

姜欣，女，1968年生。天津大学管理与经济学部博士研究生。主要研究方向为水下移动观测平台质量管理。刘玉红，女，1971年生。天津大学机械工程学院副教授。宋诗军，男，1990年生。天津大学机械工程学院硕士研究生。王延辉，男，1979年生。天津大学机械工程学院副教授。