保持参数分布状态的有限元变形网格B样条曲面重建算法
李 涛 刘 浩 何 纲
1.苏州科技学院,苏州,215009 2.南京航空航天大学,南京,2100163.河海大学,常州,213022
保持参数分布状态的有限元变形网格B样条曲面重建算法
李涛1刘浩2何纲3
1.苏州科技学院,苏州,2150092.南京航空航天大学,南京,2100163.河海大学,常州,213022
针对变形前后的有限元网格模型及原始曲面模型,提出一种保持参数分布状态的B样条曲面重建算法。在裁剪区域,通过对原始曲面进行平移、延伸、截取及重新参数化等操作,构造初始拟合曲面;在非裁剪区域,在垂直于大曲率边界的参数方向上插入截面线并重新参数化两条大曲率边界,用双向蒙皮的方法重建拟合曲面。然后进入重新参数化网格点和重新拟合曲面的迭代过程,直至满足终止准则。在曲面迭代修改过程中,通过计算基函数的极值点给出一种更精确的欠约束区域判定方法;利用插值四边/三角细分算法细化粗糙网格模型,补充约束条件,提高拟合曲面的光顺性;借助拟合曲面补充边界约束条件,结合网格点插值和形状保持约束,改进裁剪曲面的拟合精度。实验结果验证了算法的有效性。
参数分布;欠约束区域;双向蒙皮;插值四边/三角细分
0 引言
在板料成形计算机辅助工程(CAE)分析过程中,通常要把计算机辅助设计(CAD)得到的曲面模型划分成有限元网格单元,然后用CAE软件模拟冲压过程进行成形性评估,再修改曲面模型并返回至CAE系统继续分析[1]。这是一个循环反复的过程。由于经过分析以后的网格模型往往发生变形,原来的曲面模型不能直接输入到CAD/CAM系统中,必须把修改后的网格转化成曲面模型,因此,设计高效、稳定的曲面重建算法对缩短产品设计周期、节省开发成本具有极其重要的作用。
曲面重构是逆向工程、计算机图形学和CAD等领域的一个经典问题,目前已有大量的研究成果[2-8]。按照待拟合数据是否规则,传统的自由曲面重构算法大致可以分为两大类:一类是针对有序的截面数据,利用蒙皮的方法构造单张或多张曲面[2-3];一类是针对大规模的散乱数据,通过拟合的方法构造满足一定精度和光顺性要求的逼近曲面[4-6]。由于对原始几何信息未知,在曲面重建时不可能考虑参数分布,而不良的参数分布可能导致曲面在随后的网格剖分时产生大量的非结构三角网格,不利于有限元分析。另一方面,有限元网格不同于逆向工程中的测量数据,网格通常划分得比较稀疏,且自适应采样的过程也往往使网格点分布不够均匀。因此,完全借助逆向工程软件或按照传统的曲面拟合方法对有限元网格进行曲面反求,效果并不理想。由于有限元网格模型是由CAD曲面模型转化而来的,变形网格对应的原始几何信息是已知的,且这些信息正是需要计算出来进行分析和比较的,在曲面重构时应该予以考虑。
关于有限元网格模型的曲面重建,文献[6]假设已知变形前后网格点的对应关系,采用类似逆向工程里的方法直接进行B样条曲面的重建,没有考虑网格分布不均时的异常处理和拟合曲面的参数分布;文献[7]把对原始曲面的迭代修改和对变形网格的曲面重构结合在一起,但是曲面修改的方法难以有效地控制边界误差;文献[8]把双向蒙皮、曲面扫掠、延伸等正向设计的思想用于有限元网格模型的曲面重建,取得了较好的效果,但是仍有一些问题没有解决:①重建裁剪曲面时没有考虑原始曲面参数分布;②对于非裁剪区域,双向蒙皮的方法可以构造出逼近程度较高的初始拟合曲面,但是当边界曲率变化较大,特别是当边界呈“U”形或“S”形时,蒙皮曲面的参数分布不够理想;③对拟合曲面进行迭代修改时,按照文献[4]的方法在被裁剪区域或稀疏网格点处补充形状保持约束条件,虽然可以保证约束方程组的可解性,但是当大量欠约束区域存在时,该方法构造的拟合曲面光顺性较差。
本文主要解决上述几个关键问题,根据输入的原始曲面和网格及变形网格模型,重建新的曲面模型。本文假设变形前后的网格并无确定的对应关系,但是变形网格已经划分为若干个与原始曲面模型相对应的区域。
1 非裁剪域B样条蒙皮曲面的构造
1.1非裁剪域的判定
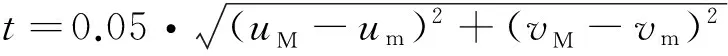
1.2截面线的插入
在一些钣金件模型中,通常会含有一些狭长的区域,这些区域大都含有四条比较规则的边界线,可以直接用双向蒙皮方法构造插值四条边界的初始拟合曲面[8],但是由于缺乏对曲面内部形状的约束,当边界曲率比较大时,内部网格点与曲面的偏差会比较大,曲面内部呈现拱起或凹陷的现象,如图1所示算例,图1b是对图1a中的网格直接插值四条边界得到的蒙皮曲面,内部网格点的最大误差(如无特别说明,本文所说的误差均为相对误差,即绝对误差与曲面片最小轴向矩形包围盒对角线长度的比值)为3.7310-2,平均误差为1.8810-2。另一方面,当曲面边界曲率较大时,由于网格点分布不均匀(如图1a中曲率较大的两条对边),蒙皮曲面的参数分布往往不够理想,如图1d所示。解决上述2个问题的方法是在垂直于大曲率边界的参数方向上插入一条内部截面线,这样一方面可以在蒙皮时增加内部截面线约束,另一方面,可以利用此截面线调整与其相交的两条对边的参数分布,使之协调一致。

(a)网格模型

(b)蒙皮曲面光照图

(c)原始曲面的参数分布

(d)曲面与原曲面参数对比图1 直接插值四条边界的双向蒙皮曲面
在两条大曲率对边上各选取离中点最近的一点作为截面线候选起始点,然后比较两条曲线在相应点处的曲率值。为了提高算法的稳定性,取曲率较小的候选点作为新截面线的起始端点,如图1a中的A点。以边界线在该点的切线方向为参考方向d1,在变形网格上沿网格边搜索一条大致垂直于该方向的路径,直至对边边界,如图1a中的路径AB。由于有限元网格具有自适应采样的特点,一般而言,上述方法得到的路径并不光滑,作为曲面蒙皮和重新参数化至关重要的一条中间截面线,需要进一步调整。方法如下:在这条新的截面线上寻找一条光滑的最长子路径,如果这段子路径的顶点数大于2,且其走向d2与前面的参考方向d1大致垂直,则把d2作为投影方向,向两条对边边界重新投影并延伸这段光滑子路径,得到修正后的截面线。如果网格模型的结构性很差,在初始截面线上找不到上述光滑子路径,则直接从起始端点开始根据参考方向d1向对边边界投影。如果对边边界的曲率比较大,这样直接投影的效果不一定理想,可以根据投影曲线与对边边界的夹角情况进行迭代修改,使新的截面线与两条相交边界的夹角之差最小。
1.3重新参数化边界线
在构造插值四条边界的双向蒙皮曲面时,由于网格模型具有自适应采样的特性,对于曲率较大的两条对边,传统的参数化方法有时不能得到协调的参数分布,从而影响蒙皮曲面的参数分布,如图1d所示。因此,需要重新参数化曲率较大的两条对边,以调整蒙皮曲面的参数分布。文献[9]在计算降阶前后两条Bezier曲线的Hausdorff距离时,设置局部曲率极值点或参数中点为分段点,然后对逼近曲线的参数引入分段线性变换,从而实现曲线的重新参数化。本文借鉴该方法,利用新插入的中间截面线调整两条大曲率对边的参数分布。

(1)
经过修改后,中间截面线与该边界交点参数由m1变为m,其他点的参数也随之做线性调整,另一条曲线的调整方法类似。图2是对图1所示算例插入一条中间截面线并调整参数后得到的蒙皮曲面,内部网格点的最大误差为9.49×10-3,平均误差为4.09×10-3。比较可见,插入一条截面线后,蒙皮曲面无论在参数分布还是拟合精度上都有较大的改善。

(a)蒙皮曲面与原曲面参数对比

(b)蒙皮曲面光照图图2 插入一条中间截面线后构造的蒙皮曲面
2 裁剪区域B样条基曲面的构造
初始拟合曲面的曲面品质和逼近精度对于最终的拟合结果都有至关重要的影响。作为参数化投影基曲面,采用B样条拟合曲面比最小二乘拟合平面可以得到更好的参数化结果[3]。
关于裁剪曲面的拟合,由于被裁剪区域几何信息的缺失,初始基曲面的构造是一个难题。因为裁剪曲面的外环边界形状不定,难以直接根据裁剪边界确定基曲面的参数走向。因此,用曲面重建的方法构造的拟合曲面与原始曲面的参数分布往往有很大的差异[8]。文献[4]用最小二乘拟合平面作为投影基曲面参数化拟合数据。这种方法不适合大曲率曲面,因为投影参数化方法可能导致参数分布很不理想。
本文通过平移并修改原始基曲面的方法构造与之有相同参数分布的裁剪曲面。对每一张曲面片,根据变形前后网格模型估算一个大致的偏置矢量,把原始曲面加上偏置矢量后得到的新曲面作为裁剪曲面的初始近似。以新曲面为投影面计算变形网格点的参数,同时得到网格点到其投影点的距离,即拟合误差。如果所有网格点的误差满足给定阈值,即变形曲面刚好是原曲面的一个近似平移,则平移后的新曲面即可作为最终的拟合曲面;否则,检查是否有边界点没有投影到基曲面上,若出现上述情况,则根据最大偏离点的位置延伸基曲面,从而使所有网格点都投影到基曲面上。
3 基于误差约束的B样条曲面迭代修改
按照上述方法构造的初始拟合曲面,特别是裁剪曲面的初始基曲面,往往不能满足用户的误差要求,需要进一步修改,以降低拟合误差。主要思想是用最新得到的拟合曲面作为参数化投影曲面,重新计算网格点参数和误差,如果达到误差需求或最大迭代次数,则停止计算;否则重新拟合。下面着重介绍曲面迭代修改过程中的一些关键技术细节。3.1基曲面的预处理
原始曲面模型本身可能存在一些设计缺陷,如裁剪曲面的基曲面过大,参数分布不佳等。直接以这种曲面的偏置面为初始曲面进行迭代修改,往往难以保证拟合曲面的精度和光顺性,因此,对这种有缺陷的基曲面需要加以修改。
若裁剪曲面的基曲面过大,如图3a、图3b所示,基曲面的大部分区域属于“无用”区域被裁剪掉,且这部分区域在曲面重新拟合过程中没有任何作用,同时保留区域的约束作用被弱化,故采用曲面截取的方式[10]去掉部分“无用”区域。图3c是截取后的裁剪曲面及其基曲面。

(a)原始裁剪曲面

(b)原始裁剪曲面及其基曲面

(c)截取后的裁剪曲面及其基曲面

(d)重新参数化后的裁剪曲面及其基曲面图3 初始基曲的预处理示例
若基曲面的参数分布不佳,不仅降低拟合算法的效率,而且影响后续的应用,如有限元网格划分,数控刀轨生成等。引起曲面参数分布不理想的原因主要有两个:一是B样条基函数的节点布局不均匀,二是曲面控制顶点的空间分布不均匀。对于前者,通过插入或删除节点[10]方法使其分布尽量均匀,即计算基函数相邻互异节点的节点距ki和节点距的平均值ka,若ki>rka,则在两节点之间插入[ki/(rka)] - 1个节点,其中[·]表示取整操作,r为比例因子,通常可以取3~6之间的值;若ki 3.2约束方程组的建立 根据网格点参数和初始拟合曲面 (2) 可以建立约束线性方程组 AD=B (3) 式中,di,j为曲面控制顶点;Ni,k(u)与Nj,l(v)分别为k次和l次B样条基函数;A为将网格点参数代入曲面基函数得到的系数矩阵;D为由曲面控制顶点di,j构成的未知量;B为由网格点坐标构成的常矢量。 由于有限元网格点分布的不均匀性以及大量裁剪曲面的存在,方程组可能出现欠约束与过约束同时存在的问题,即系数矩阵A可能行或列不满秩,或者两者都不满秩。这给线性系统(式(3))的求解带来了困难。为了保证(式(3))解的唯一性与稳定性,本文采取的策略是通过寻找欠约束区域并为之适当补充约束条件,构造一个系数矩阵恒满足列满秩的新的线性系统: (4) 3.3欠约束区域的判定 文献[4]用均匀B样条基函数节点区间的中间部分作为有效域进行孔洞识别,如果落在有效域内的网格点参数个数少于一定的阈值,则认为该区域为欠约束区域,需要在此补充形状保持约束条件: -0.25(di-1,j-1+di-1,j+1+di+1,j-1+di+1,j+1) + 0.5(di-1,j+di,j-1+di,j+1+di+1,j)=di,j (5) 从而提高了最小二乘解的稳定性。但是上述有效域的判别方法并不适应于一般的非均匀B样条曲面,因为当基函数节点分布不均,特别是当基函数含有内部重节点时,最大值点可能出现在节点附近。因此,在此给出一种更加准确的欠约束区域识别方法。 图4 有效域示意图 3.4混合网格的插值细分 在逆向工程中,通过对欠约束区域施加顶点形状保持约束可以提高最小二乘解的稳定性[4]。然而,对于比较稀疏的有限元网格,由于大量欠约束区域的存在,该方法的拟合效果并不理想。在图5所示的算例中,图5c是对图5a中的网格用文献[4]的方法拟合得到的结果,虽然最大误差(3.23×10-3)达到一般的工程要求,但是拟合曲面的光顺性较差。导致拟合曲面品质较低的主要原因是网格模型过于粗糙,插值网格点位置的“刚性”约束条件不足。解决上述问题的一个有效办法是增加网格点密度,补充“刚性”约束条件。显然,线性插补会降低网格模型的光顺性,影响拟合曲面的品质,因此考虑网格模型的插值细分。 (a)待拟合的网格模 (b)细分二次后的网格图 (c)拟合原网格所得曲面 (d)拟合细分网格所得曲面图5 通过对网格插值细分增加约束条件 由于有限元网格大都是由四边形和三角形构成的混合网格,本文采用四边/三角混合网格的插值细分。目前关于混合网格插值细分算法的研究比较多[11-13],针对有边界的不规则混合网格插值细分,本文采用文献[13]的方法,把细分算法分解为线性分割和几何平均两个过程,根据插值细分与相应逼近型细分的关系,把线性分割得到的新边点和新面点加上相应偏置量,得到最终的新位置,其中新边点和新面点的偏置量是以网格顶点相对于相应逼近型细分点的偏置量为基础计算得到的,权因子为相应的逼近型细分模板。图5b是对图5a所示网格细分二次所得到的网格图,比较图5a和图5b可见,细分以后网格点更加稠密,网格模型也更加光顺,图5d是用细分后的网格拟合得到的曲面模型,最大误差为2.73×10-3,与图5c相比,光顺性有了显著的提高。 网格细分方法在增加“刚性”约束条件的同时也加大了运算开销,因此,网格细分与否是以网格点是否过于稀疏或者是否存在大量欠约束区域为判定准则的。 3.5狭长裁剪面的迭代修改 (a)网格模型 (b)拟合曲面图 (c)图6b的局部放大 如1.2节所述,钣金件几何模型中的狭长区域,大部分可以用双向蒙皮的方法重构出高精度和高品质的拟合曲面,但是也有部分狭长区域没有形状规则的四条边界,如图6a所示的网格模型,这时只能作为裁剪曲面来处理。由于基曲面的大部分区域被裁剪掉,因此曲面迭代修改时会出现几何约束不足的问题。虽然文献[4]根据文献[14]给出了形状保持约束,但是当存在大量欠约束区域,尤其是基曲面的边界无法得到有效控制时,拟合曲面的光顺性难以得到保证,原因是Farin的持久准则[14]实际上是一个离散形式的Euler-LagrangePDE,边界约束必不可少。本文给出的解决方案是,将前一次拟合曲面的边界信息和网格点一样,作为曲面修改的“硬约束”,其他内部欠约束区域作为“软约束”由形状保持准则给出。作为“硬约束”,初始拟合曲面的边界误差不能太大,如果误差过大,如绝对误差大于0.5mm或相对误差大于0.05,则将该曲面先做变形处理:根据网格点的误差计算曲面的法向偏置量,如果曲面采样点参数在裁剪域内,则其偏置量由邻近网格点的偏置量内插得到;否则,由已知偏置量的邻近点外插得到,然后根据偏置信息重新拟合曲面。这样得到的变形曲面比原来的拟合曲面更加“贴近”网格模型,可以用来补充边界插值约束条件。把边界点插值约束和内部形状保持约束(式(5))加入线性系统(式(3))中,得到最终的约束方程式(4)。在图6所示的算例中,图6b是用上述方法对图6a拟合的结果,最大误差为7.60×10-4,平均误差为1.16×10-4,最大绝对误差为0.436mm。笔者同时用文献[7]和文献[4]的方法对此算例做了实验,文献[7]在去掉光顺项约束后,最大绝对误差仍为0.808mm,而文献[4]的方法由于拟合曲面严重扭曲而导致算法失败。 (d)拟合裁剪曲面及其基曲面图6 狭长裁剪面示例 图7是一个综合算例,其中图7a和图7b分别为原始曲面和拟合曲面的线框图,图7c是拟合曲面的光照图。图8是另一模型的拟合结果。两个算例的运行情况见表1,其中最大绝对/相对误差是整个模型所有拟合曲面的绝对/相对误差的最大值,平均绝对误差是整个模型所有拟合曲面绝对误差的平均值。本文所有算法都用C++语言编程实现,程序运行的软硬件环境为WindowsXP操作系统,VC++ 6.0编译器和主频2.0GHz,内存2.0GB的笔记本电脑。由算例可知,本文算法具有较高的精度和较快的速度,拟合曲面不仅具有较好的光顺性,而且具有与原始曲面基本一致甚至更佳的参数分布状态。 (a)原始曲面线框图 (b)拟合曲面线框图 (c)拟合曲面光照图图7 综合算例1 (a)原始曲面线框图 (b)拟合曲面线框图图8 综合算例2 算例曲面片数网格单元数网格点数最大绝对误差/最大相对误差平均绝对误差运行时间(s)算例119015933158910.245mm/2.94´10-22.18×10-2mm55.4算例240623475217380.460mm/1.83´10-22.40×10-2mm52.1 基于有限元网格与逆向工程中的大规模网格模型的不同,提出了更有针对性的有限元变形网格曲面重建算法。曲面蒙皮、延伸、截取、重新参数化等许多正向设计的方法被用于初始拟合曲面的构造;在曲面的迭代修改过程中,通过计算基函数的极值点给出稳定性更好的有效域判别方法;通过混合网格插值细分算法细化部分稀疏的网格,补充必要的插值约束条件,提高了拟合曲面的光顺性;利用最新拟合的基曲面或其变形曲面,补充部分狭长裁剪曲面的边界插值约束,给出了稳定性更高的裁剪曲面拟合算法。本文方法构造的拟合曲面不仅光顺性好,误差小,运算效率也很高,达到了实时的要求。更为重要的是,拟合曲面与原始曲面具有基本一致甚至更优的参数分布状态,可以几乎无需修改而直接用于后续的CAE或CAM。当然,部分狭长区域裁剪曲面的拟合误差虽然较现有方法有所改进,但有时仍然偏高,这是算法有待进一步提高的地方。 [1]陈文亮. 板料成型CAE分析教程[M], 北京:机械工业出版社, 2005. [2]ParkH.B-splineSurfaceFittingBasedonAdaptiveKnotPlacementUsingDominantColumns[J].Computer-AidedDesign, 2011,43(3): 258-264. [3]MaWeiyin,KruthJ.ParameterizationofRandomlyMeasuredPointsforLeastSquaresFittingofB-splineCurvesandSurfaces[J].Computer-AidedDesign, 1995,27(9):663-675. [4]谭昌柏, 周来水, 张丽艳,等. 裁剪B样条曲面重建算法研究[J]. 中国机械工程, 2007, 18(19): 2366-2370. TanChangbai,ZhouLaishui,ZhangLiyan,etal.ResearchonTrimmedB-splineEurfaceReconstruction[J].ChinaMechanicalEngineering, 2007, 18(19): 2366-2370. [5]HuangYunbo,QianXiaoping.DynamicB-splineSurfaceReconstruction:ClosingtheSensing-and-modelingLoopin3DDigitization[J].Computer-AidedDesign, 2007,39(11): 987-1002. [6]谭光华, 陈志杨, 张三元,等. 基于原始曲面信息的变形网格的曲面重构[J]. 中国机械工程, 2009, 20(1): 38-43. TanGuanghua,ChenZhiyang,ZhangSanyuan,etal.SurfaceReconstructionforDeformedMeshBasedonOriginalSurfaceInformation[J].ChinaMechanicalEngineering, 2009, 20(1): 38-43. [7]曾建江, 李卫国, 陈文亮. 基于有限元网格变形的飞机外形曲面修改[J]. 南京航空航天大学学报, 2008, 40(4): 534-538. ZengJianjiang,LiWeiguo,ChenWenliang.MappingAircraftSurfacesbyDeformationofFiniteElements[J].JournalofNanjingUniversityofAeronautics&Astronautics, 2008, 40(4): 534-538. [8]LiTao,WangYuguo,ChenWenliang.PiecewiseSmoothSurfacesReconstructionforFiniteElementMixedMeshes[C]//InternationalConferenceonDigitalManufacturing&Automation.Changsha,China, 2010: 90-94. [9]ChenXiaodiao,MaWeiyin,PaulJ.Multi-degreeReductionofBezierCurvesUsingReparameterization[J].Computer-AidedDesign, 2011,43(2):161-169. [10]PieglL,TillerW.TheNURBSBook[M].2Ed.Berlin:SpringerPress, 1996. [11]JiangQingtang,LiBaobin,ZhuWeiwei.InterpolatoryQuad/triangleSubdivisionSchemesforSurfaceDesign[J].ComputerAidedGeometricDesign, 2009, 26(8): 904-922. [12]LinShujing,LuoXiaonan,YouFang,et.al.DeducingInterpolatorySubdivisionSchemesfromApproximatingSubdivisionSchemes[J].ACMTransactiononGraphics, 2008, 27(5):article146(1-7). [13]LinShujing,LuoXiaonan,XuSonghua,etal.ANewInterpolationSubdivisionSchemeforTriangle/QuadMesh[J].GraphicalModels, 2013, 75(5): 247-254. [14]FarinG,HansfordD.DiscreteCoonsPatches[J].ComputerAidedGeometricDesign, 1999, 16(7): 691-700. (编辑王艳丽) Reconstruction of B-spline Surfaces from Finite Element Deformed Meshes with Consistent Parametric Distribution Li Tao1Liu Hao2He Gang3 1.Suzhou University of Science and Technology,Suzhou,Jiangsu,215009 2.Nanjing University of Aeronautics and Astronautics,Nanjing,210016 3.Hohai University,Changzhou,Jiangsu,213022 According to the information of original surfaces, original meshes and deformed meshes, a method for reconstructing B-spline surfaces with consistent parametric distribution was presented. In trimmed regions, initial fitting surfaces were constructed by some operations on original surfaces such as translation, extension, segment and reparametrization, etc. In untrimmed regions, bidirectional skinning method was adopted for the production of initial surfaces after inserting section lines across the highly curved boundaries and revising their parameterization. Then a loop of reparameterizing the nodes and refitting the surfaces proceeded until some ending rules were satisfied. During the process of iteration, a more precise method was presented for determining under-constrained regions by calculating extreme points of basis functions; fairness of the fitting surfaces was improved evidently by splitting coarse meshes to provide enough constraints with interpolatory quad/triangle subdivision scheme. Fitting precision is improved for trimmed surfaces by dint of boundaries and internal nodes interpolation constraints together with shape preservation constraints of under-constrained regions. Test results indicate effectivity of the proposed method. parametric distribution; under-constrained region; bidirectional skinning;interpolatory quad/triangle subdivision 2014-02-18 国家自然科学基金资助项目(51175248,51375141);江苏省省属高校自然科学研究资助项目(12KJB460009) TP391< class="emphasis_italic">DOI :10.3969/j.issn.1004-132X.2015.05.019 李涛,男,1978年生。苏州科技学院数理学院讲师。主要研究方向为CAGD。发表论文10余篇。刘浩,男,1972年生。南京航空航天大学机电学院副教授。何纲,男,1975年生。河海大学机电学院副教授。











4 算例与应用





5 结语

