例谈借助几何直观促进问题解决
朱向东


几何直观主要是指利用图形描述和分析问题。它的优越性已勿需多谈,然而,在当前的教学实际中,几何直观的应用大多还只局限于几何图形内容的学习,常态的应用还较少,几何直观的优越性还没有得到凸显,尤其是学生利用图形描述和分析问题的意识还没有得到足够的重视和引导。下面,笔者根据自身的教学实践,结合几个具体的实例谈谈几何直观在数学问题解决中的应用。
例1 某校要从3名男同学和2名女同学中各选出1人代表学校参加“少儿戏曲大赛”,有多少种不同的组队方案?
图1
解析:引导学生将生活问题转化成数学问题,用图形和符号来表示量。可以用画图的方式来表示出组队的情况,如图1可以用三个圆代表三名男生,并用数字加以区分,用2个长方形代表2名女生,并用数字加以区分,再引导学生用连线的方法表示出搭配的方法。接着引导学生看图说一说组队的方案,让学生感受画图不仅能清楚地表达出每一种组队的方案,还能简洁、直观地表明共几种搭配方法,让学生感受了画图的价值,同时还渗透了符号意识。只有让学生体会到画图对寻求解题思路带来的益处,才会进而产生画图的兴趣,学生的几何直观能力才会得到发展。
例2 3个小朋友拿着同样多的零花钱凑在一起买铅笔。小刚和小强分别比小勇多拿了6支,他俩各给了小勇6角钱,请问每支铅笔的价格是多少?(铅笔的型号相同)
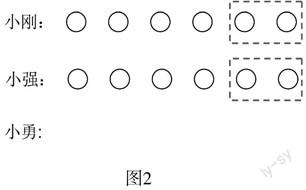
图2
解析:首先通过讨论交流,使学生明确:3人拿同样多的钱买铅笔,那么三人的所得也应该是相同的。若用一般方法进行分析,多数学生会一头雾水;运用几何直观画图,效果就大不一样了。假如用一个圆圈表示多拿的1支铅笔,那么三人多拿的铅笔的情况如图2所示。要想公平,多出的12支铅笔应该是平均每人分4支。那么,小刚和小强就应各取出2支铅笔给小勇,即小勇按理也应分得4支铅笔,值2个6角,这样就很清楚地看出每支铅笔的价格是3角钱了。
例3 妈妈的年龄是小玲的4倍,妈妈比小玲大24岁,妈妈和小玲各是多少岁?
解析:这是一道比较典型的年龄问题。此题要求两个量,用两种不同的方式(倍、差)来表示这两个量之间的关系,对低年级学生而言,比较抽象,学生不好理解,用一般方法难以奏效。教师若能引导学生通过画线段图表示题目中的已知条件和问题,结合线段图去观察思考,相信大部分学生都能顺利解决。从图3的线段图中,学生可以直观地看出,小玲的年龄用1份表示,妈妈的年龄就是这样的4份,多出的这3份就是妈妈比小玲大的24岁,所以1份表示的年龄是:24÷3=8(岁),即小玲的年龄是8岁,妈妈的年龄就是:8×4=32(岁)。
图3
例4 学校食堂买来一些大米。计划吃10天,实际每天比计划多吃4千克,结果提前2天就吃完了。你能算出原计划每天吃多少千克吗?
图4
解析:引导学生分析,大米的总量怎么表示?既然可以表示为吃的天数与每天吃的千克数的积,那么就不难联想到长方形的面积也是长与宽的积,因此可以画图(长方形)来表示题目中的数量关系。进一步思考,大米的总量按计划情况怎么表示?按实际情况呢?大家能在一个图里表示清楚吗?逐步引导、指导学生画出图4。进而提问,图中的两个大长方形AEFD与ABGH的面积分别表示什么意思?二者有何关系?学生观察后,很容易发现,二者是相等的,都表示大米的总量;教师再引导观察,图中的两个长方形BEFC与DCGH(图中的阴影部分)的面积分别表示什么意思?二者有何关系?
在观察与思考中,学生认识到长方形BEFC的面积表示的是实际8天多吃的千克数,长方形DCGH的面积表示的是计划2天吃的千克数,二者相等。因为每天都比计划多吃了4千克,所以导致提前2天吃完,8天总共多吃的千克数其实就是原计划2天吃的千克数。即:4×(8-2)=2×计划每天吃的千克数,计划每天吃的千克数就是4×(8-2)÷2=12(千克),问题迎刃而解。
例5学校体育组老师新买了3个篮球和4个排球,一共用了424元,一个篮球比一个排球贵13元,篮球和排球单价各是多少元?
解析:通过图解,把题意转化成图5,从图中学生一眼就能看出,从总钱数中减去3个13元,剩下的钱数就是7个排球的价钱,从而可以求出排球的单价,列式为(424-13×3)÷(3+4)=55(元)。篮球的单价则为55+13=68(元)。通过几何直观,把“数”转化为“形”,学生清楚地看出数量之间的关系,化难为易,迅速发现解题思路。
图5
再如,有关分数的实际问题,长方体、正方体等立体图形的表面积和体积问题、周期问题、植树问题等,都可以利用几何直观进行教学,促进学生的思维能力和分析、解决问题能力的提升。
综上所述,数学教师都要做一个有心人,不仅在图形与几何领域的教学中要重视几何直观,而且在整个数学教学中都应该重视几何直观,把几何直观能力的培养贯穿于学生的整个数学学习过程。学生几何直观能力的培养,只有潜移默化地融入到平时的课堂教学和学习中,植根于学生个体经验的积累中,效果才会明显。当然也需要根据不同年级、不同学生的实际情况分层次提出不同的要求,需要根据教学内容有意识地长期训练,从而让学生更好地利用图形来描述和分析问题,提升他们的数学素养。
◇责任编辑:徐新亮◇

