考虑基质收缩的煤层气物质平衡方程

曹煜，林璠，田慧君

（成都理工大学能源学院，四川成都610059）

考虑基质收缩的煤层气物质平衡方程

曹煜，林璠，田慧君

（成都理工大学能源学院，四川成都610059）

煤层气资源量丰富，为了探讨煤层气的地下储量，根据体积守恒原理，推导出适用于煤层气藏的物质平衡方程。煤层结构与常规储层结构不同，由煤基质块与割理组成，赋存形式主要以游离态和吸附态为主，其中吸附态占最主要部分。充分考虑了水侵量、岩石和流体的弹性变形，以及气体解吸变形等气藏内的驱动机理，并引入Palmer和Mansoori创建的基质收缩模型，利用弹性模量描述煤层体积随压力变化的影响，推导出一种新的适用于煤层气藏的物质平衡方程。通过气田实际数据，应用公式计算出煤层气总储量为127.784×108m3，其中包括游离气储量0.904×108m3，吸附气储量126.88×108m3。该物质平衡方程式在实践中具有较好的指导意义。

煤层气；物质平衡方程；游离气；吸附气；基质收缩

煤层气是一种自生自储的天然气，基本上没有经历大规模的二次运移和聚集作用，其富集因素主要取决于煤层本身的发育程度和封盖保存条件［1］。煤的孔隙结构由煤基质块和割理组成，少量天然气以游离态的形式赋存于割理中，而大量天然气以吸附态的形式吸附在煤基质表面［2，3］。游离状态的天然气约占10%～20%，呈吸附状态的天然气可占70%～95%，还有少量的天然气溶解在煤层的地下水中（由于量极少，常予以忽略不计）［4］。

1993年King提出在煤层气藏中应用物质平衡方程，并推导出计算游离气量和吸附气量的公式［5］。随后Seidle于1999年的研究也推动了物质平衡方法在煤层气藏工程中的应用［6］。Moghadam在2010年充分考虑了包括水侵量、岩石以及流体弹性变形和煤层气或者页岩气的解吸变形等驱动机理，推导出改进的气藏通用物质平衡方程式［7］。本文中，基于Moghadam的推导，考虑了煤层气藏中应力敏感造成的煤基质的压缩变形，引入Palmer和Mansoori创建的基质收缩模型，利用弹性模量描述煤层体积随压力变化的影响［8］，推导出一种新的适用于煤层气藏的物质平衡方程。

1 物质平衡方程的推导

1.1 通用物质平衡方程

假设初始压力条件下，游离气GF全部存储在孔缝中，根据物质守恒原理，考虑气藏中各种驱动机理，建立通用物质平衡方程。

原始条件下气体占有的储层孔隙体积=剩余游离气储量+水侵量+岩石与液体变形膨胀量+解吸气量。即：

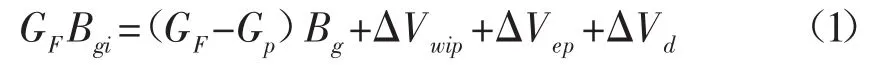
该通用方程适用于常规气藏、超压气藏、煤层气藏以及页岩气藏等。

1.2 水侵造成的孔隙体积变化量ΔVwip

在水驱气藏中，水侵造成的孔隙体积变化量ΔVwip为：

水侵量可按照前人提出的水体模型计算，例如：Schilthuis提出的稳态模型，Fetkovich拟稳态模型，Carter和Tracy，以及Van Everdingen和Hurst提出的非稳态模型，但应注意每一种模型都有它的假设条件和适用范围。

1.3 岩石和液体的弹性变化量ΔVep

在高压或应力敏感性储层中，储层岩石和液体的压缩系数很大，如果忽略储层岩石和液体弹性膨胀的影响，计算的地质储量会严重偏高。高压储层中，p/Z～Gp曲线呈两段直线，第一个直线段中，岩石和液体的膨胀量起重要作用，第二个直线段中气体的膨胀量占主导地位。Ramagost和Farshad认为岩石和液体弹性膨胀造成的体积变化量为：

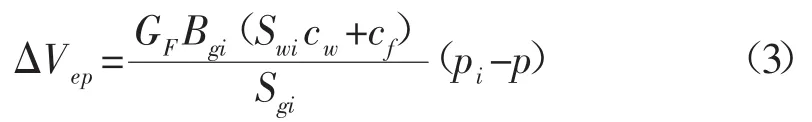
Rahman等人考虑到岩石和液体的非线性压缩变形，提出了由岩石和液体弹性膨胀造成的体积变化量的通用形式，各部分相加得到：

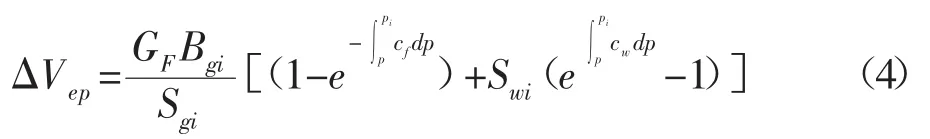
（1）考虑基质收缩引起煤基质变形：煤层气藏开采过程中，压力的变化会导致基质的收缩/膨胀，从而造成煤层孔隙体积的变化，Palmer和Mansoori创建了一种基质收缩模型，利用弹性模量描述煤层体积随压力变化的影响。

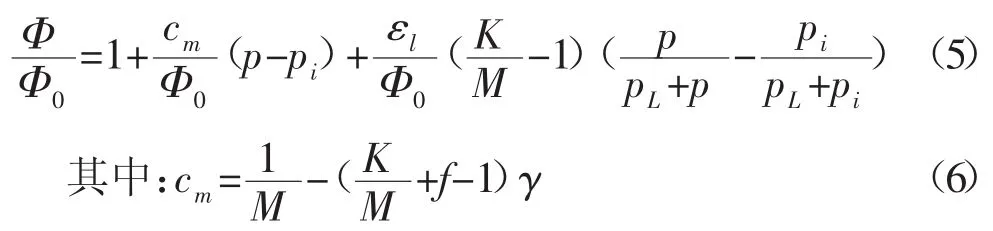
根据压缩系数的定义，得：

将方程（5）代入方程（8），得：

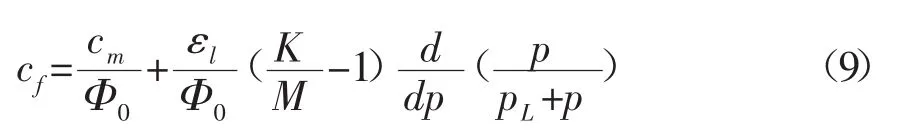
与有机质孔隙的压缩系数相比，有机质固体的压缩系数γ可以忽略，将方程（6）简化为，代入方程（9），得：

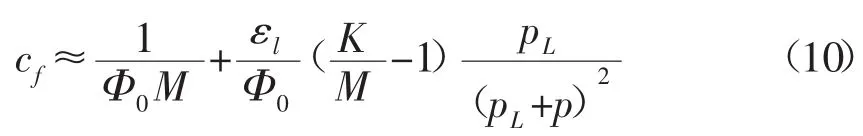
所以煤层与液体的弹性变化量ΔVep表示为：

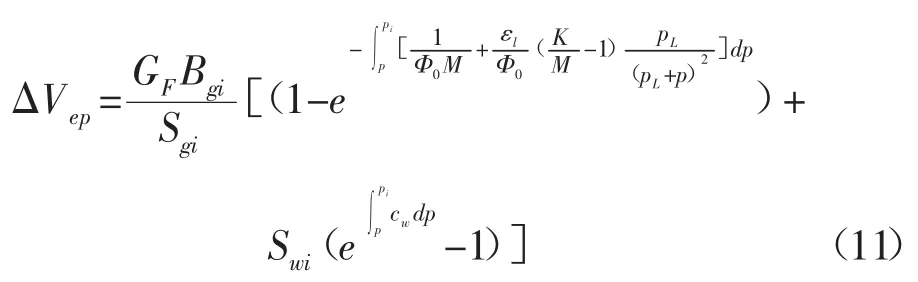
（2）不考虑煤层基质变形，假定cf、cw是定值：在煤层气生产过程中，如果cf、cw是定值，（4）式可以简化为：

由于ex≈1＋x，所以式（12）可以进一步简化为：

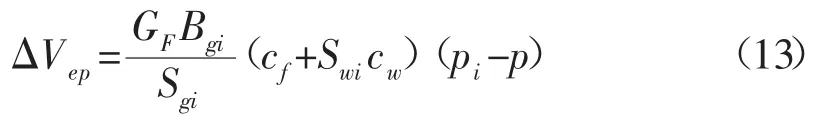
1.4 煤层气解吸量ΔVd

煤层气的储存机理与常规气藏不同。煤层气藏中，除了裂缝系统中的游离气，煤基质中还吸附了大量的煤层气。气藏开采过程中，随着地层压力下降，天然气不断从基质表面解吸出，并占据一定的裂缝空间。

用Langmuir方程描述单位质量煤层吸附气含量Gc为：

煤层吸附气的总体积为：

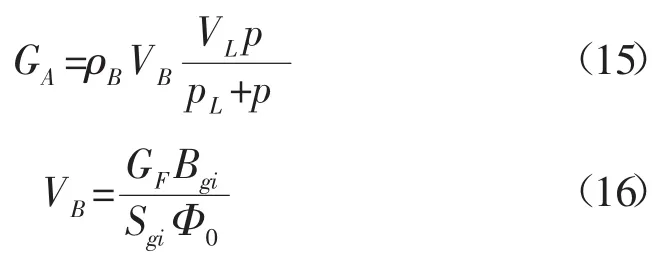
地层压力为p时，解吸出的天然气占据的孔隙体积变化量为：

1.5 煤层气藏中游离气的物质平衡方程的通式

结合式（2）、（11）和（17），将ΔVwip、ΔVep和ΔVd代入式（1），得：

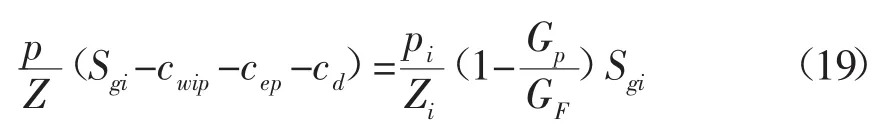
其中：

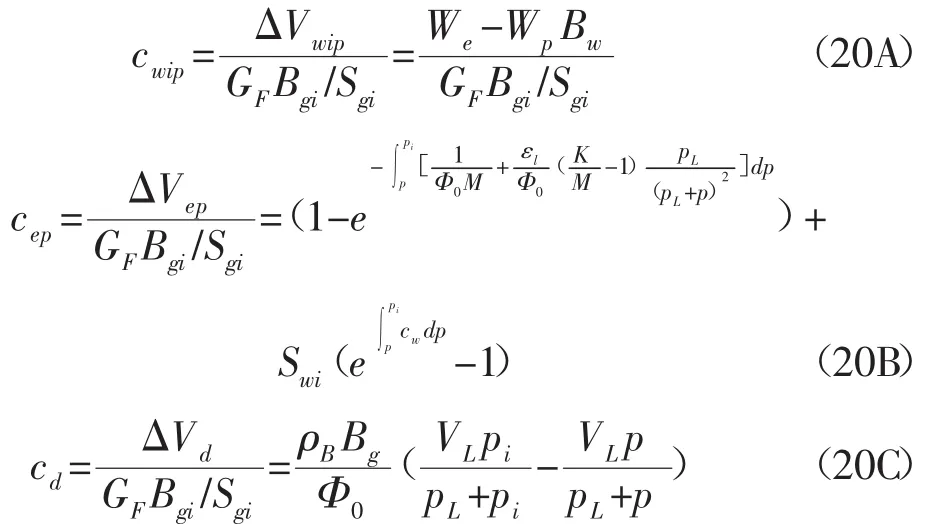
其中，cwip，cep和cd代表了每一种驱动机理引起的相对孔隙体积变化量。

将（19）式变形为：

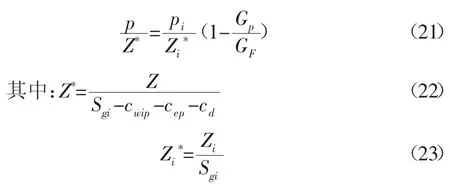
根据（21）式，在直角坐标系中绘制（p/Z*）～Gp的关系曲线，通过曲线与在x轴上的截距可求出煤层气藏游离气储量GF。

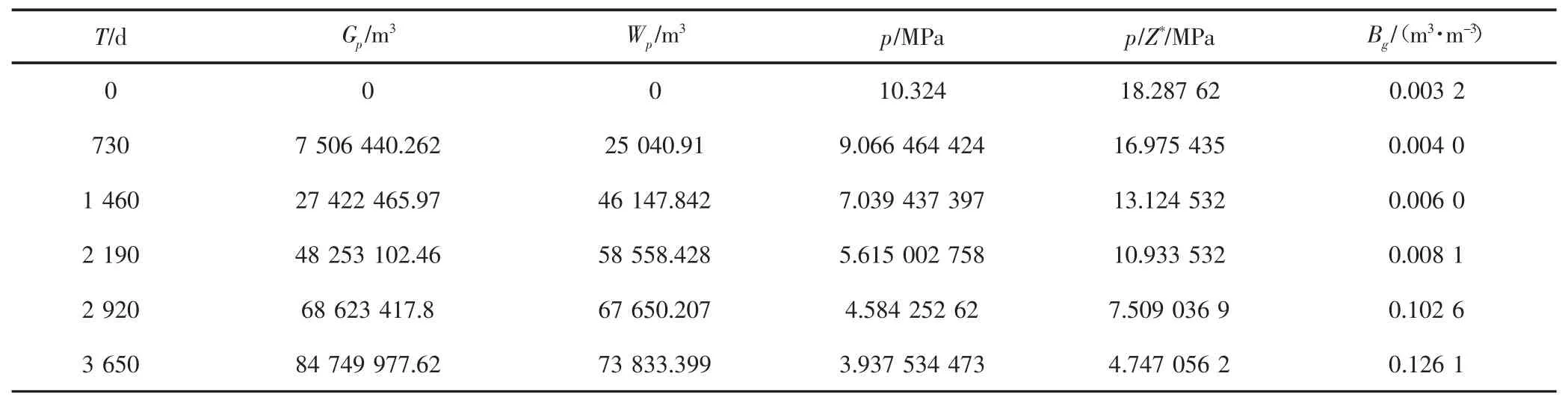
表1 煤层气井的生产数据（据GRI）

1.6 煤层气藏中总气藏储量计算

对煤层气而言，游离气的地下体积为GFBgi。总储量Gtotal还包含了吸附气含量GA。

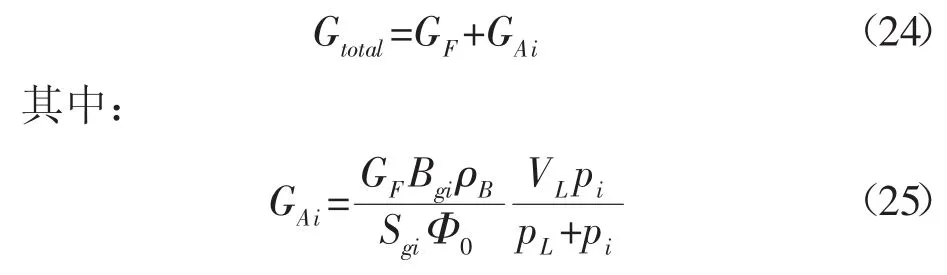
2 实例应用

以国外某煤层气藏的数据为例，应用物质平衡方程计算煤层气储量。煤层气井的生产数据和相关煤层参数（见表1和表2）。该煤层气藏不属于水侵气藏，所以水侵量We＝0。

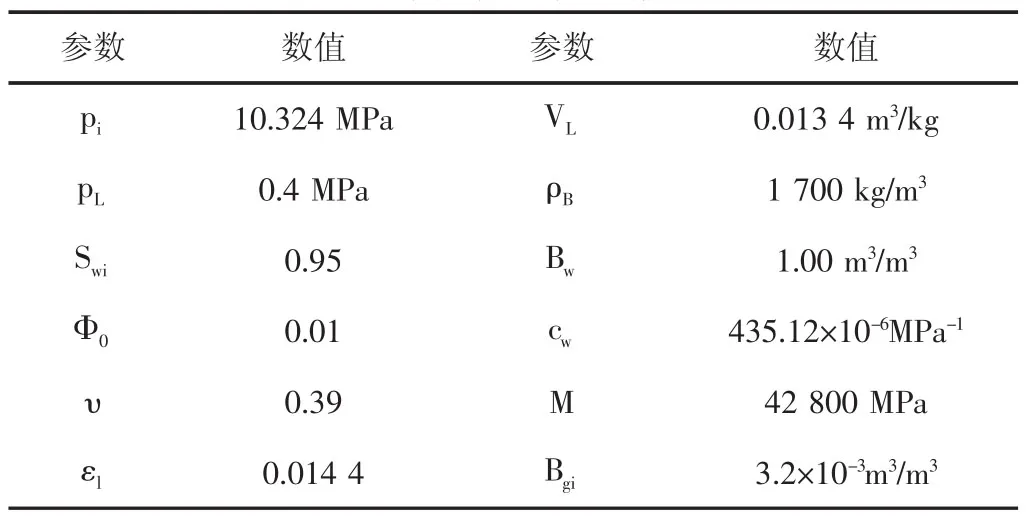
表2 煤层相关参数表（据GRI）

根据（19）~（23）式，绘制出（p/Z*）～Gp，通过曲线与在x轴上的S截距求出煤层气藏游离气储量GF为0.904×108m3；根据（25）式计算出吸附气储量GAi为126.88×108m3；根据（24）式计算煤层气总储量为127.784×108m3。

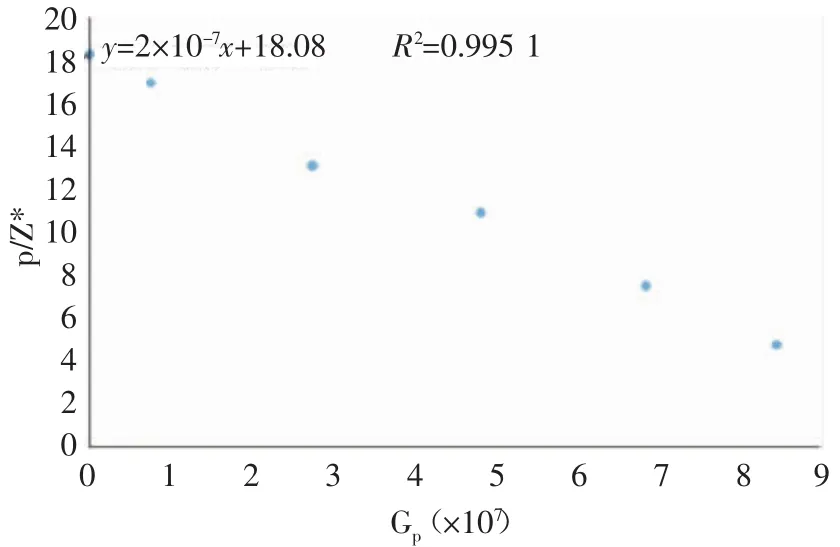
图1 p/Z*与Gp关系曲线图

3 结论

（1）考虑了水侵量、岩石以及流体的弹性压缩膨胀和煤层气或者页岩气的气体解吸等多种机理，推导出了适用于气藏的通用物质平衡方程。

（2）对于煤层气藏，考虑了应力敏感造成的煤基质的压缩变形而引起的孔隙空间的变化，引入了Palmer和Mansoori创建的基质收缩模型，利用弹性模量描述煤层体积随压力变化的影响。

（3）利用新推导出的煤层气藏物质平衡方程，计算国外某煤层气藏储量，得到结果为煤层气总储量127.784×108m3，其中包括游离气储量0.904×108m3，吸附气储量126.88×108m3。该物质平衡方程式在实践中具有较好的指导意义。

符号说明：

GF：游离气原始储量，m3；Bgi：初始条件下气体体积系数，m3/m3；Gp：累积产气量，m3；ΔVwip：水侵造成的孔隙体积变化量，m3；ΔVep：岩石和液体的弹性变化量，m3；ΔVd：煤层气解吸量，m3；We：水侵量，m3；Wp：累积产水量，m3；Bw：水的体积系数，m3/m3；p：目前地层压力，MPa；Swi：原始含水饱和度，小数；cw：水压缩系数，MPa-1；cf：储层（岩石）压缩率，MPa-1；pi：原始地层压力，MPa；Sgi：原始含气饱和度，小数；Φ：压力为p时对应的孔隙度，小数；Φ0：原始孔隙度，小数；cm：煤基质骨架膨胀系数，MPa-1；εl：兰式等温吸附中，p接近于零时的最大应力，无量纲；K：体积模量，MPa；M：约束单轴模量，MPa；pL：兰氏压力，MPa；f：系数（0~1），无量纲；γ：煤基质固体的压缩系数，MPa-1；υ：泊松比，无量纲；Gc：单位质量煤层吸附气含量，m3/kg；VL：兰氏体积，m3/kg；GA：压力为p，煤层中吸附气含量，m3；ρB：煤层密度，kg/m3；VB：煤体积，m3。

［1］贾承造.煤层气资源储量评估方法］M］.北京：石油工业出版社，2007.

［2］杨宇，孙晗森，彭小东，等.煤层气储层孔隙结构分形特征定量研究［J］.特种油气藏，2013，20（1）：31-33.

［3］秦勇，袁亮，胡千庭，等.我国煤层气勘探与开发技术现状及发展方向［J］.煤炭科学技术，2012，40（10）：1-6.

［4］李五忠，王一兵，孙斌，等.中国煤层气资源分布及勘探前景［J］.天然气工业，2004，24（5）：8-10.

［5］King R G.Material balance techniques for coal seam and Devonian shale gas reservoirs［C］.paper 20730 presented at the SPE 65th Annual Technical Conference and Exhibition，23-26 September 1990，New Orleans，Louisiana，USA.New York：SPE，1990.

［6］Seidle J P，Jeansonne M W，Erickson D J.Application of matchstick geometry to stress dependent permeability in coals［J］.paper SPE，1992，24361：18-21.

［7］Moghadam S，Jeje O，Mattar L.Advanced gas material balance in simplified format［C］.paper presented at the 10th Canadian International Petroleum Conference，Calgary，Canada，16-18 June，2009.

［8］Palmer I，Mansoori J.How permeability depends on stress and pore pressure in coalbeds：a new model［J］.SPE Reservoir Evaluation&Engineering，1998，12：539-544.

A new material balance equation for coalbed methane reservoir considering matrix shrinkage deformation

CAO Yu，LIN Fan，TIAN Huijun
（Energy College of Chengdu University of Technology，Chengdu Sichuan 610059，China）

Coalbed methane（CBM）is one of the most important natural gas resources.In order to determine original CBM in place，material balance equation was established based on volume conversation theory.Compared to conventional reservoirs，coal is composed of matrix and cleat.In coal，natural gas accumulate as free gas and adsorbed gas mainly，and adsorbed gas occupying dominantly especially.By considering water encroachment，expansion of formation and residual liquids，and gas desorption，using Palmer&Mansoori model to account for the change of coal volume induced by pressure，a new material balance equation is established.Based on the statistics from gas field overseas，calculate total original CBM in place is 127.784×108m3，including free gas of 0.904×108m3and adsorbed gas of 126.88× 108m3.The new material balance has significant guild meaning in sited reservoirs.

book=10,ebook=16

coalbed methane；material balance equation；free gas；adsorbed gas；matrix shrink age

10.3969/j.issn.1673-5285.2015.08.003

TE375

A

1673-5285（2015）08-0009-05

2015－06-08

国家科技重大专项资助项目，项目编号：2011ZX05060-002。

曹煜，男（1990-），汉族，在读硕士研究生，研究方向为油气藏工程及数值模拟。