近岸波浪在刚性植被区域传播的数值模型
王 磊,房克照, 尹 晶, 孙家文
(1. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024; 2. 国家海洋环境监测中心, 辽宁 大连 116023)
近岸波浪在刚性植被区域传播的数值模型
王 磊1,房克照1, 尹 晶2, 孙家文2
(1. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024; 2. 国家海洋环境监测中心, 辽宁 大连 116023)
基于扩展型Boussinesq水波方程,建立了波浪在刚性植被覆盖的近岸海域传播的数值模型。通过在动量方程源项中引入拖曳阻力项考虑植被对波浪的衰减作用。控制方程采用有限差分和有限体积混合格式求解,模型稳定性强,具备间断捕捉能力,能有效模拟近岸区域波浪的传播变形、破碎和处理海岸动边界问题。利用所建立模型对典型物理模型实验进行模拟,计算结果与实验结果吻合良好,表明模型可用于波浪在刚性植被覆盖海域的数值计算。
Boussinesq水波方程;刚性植被;消浪;数值模拟;波浪传播
近海岸波浪传播变形及堤坝的防浪护坡,是目前港口和海岸建设中要考虑的重要工程技术问题。传统的护岸往往采用混凝土、浆砌石等硬质材料,对生态系统会造成一定程度的破坏,干扰生态平衡。而采用自然的植被护岸,不仅能消减波能,起到防浪护岸的作用,还能维持生态系统和水动力系统的平衡,改善生态环境[1-3]。鉴于此,众多学者针对植被消减波能效果以及对相关水动力的影响开展研究[2-11]。
考虑到问题的复杂性和现场实测及物理模型实验的局限性,数学模型建立和计算仍然是开展植被消浪研究的重要手段[6]。相比于相位平均类模型(在波浪周期上进行平均),相位识别类波浪模型能提供更加精细的水动力要素而被广泛应用,在此基础上考虑植被对波浪的作用即形成适用于植被覆盖区域波浪传播的数学模型。现有的此类数学模型大致可以分为三类:一是基于雷诺平均的纳维—斯托克斯方程的数值模型[7];二是浅水方程模型,主要包括完全非线性浅水方程数学模型[8]和Boussinesq方程数值模型[9-10];三是基于缓坡方程的数值模型[11]。纳维—斯托克斯方程模型虽然可以很详细地描述流场,但是其计算代价昂贵,尤其是对于水平二维问题,因此适用性有限。完全非线性浅水方程模型相对较简单,计算效率高,但是这类模型仅能模拟短距离波的传播,不能考虑长距离传播和绕射等短波效应,尤其在处理近岸植被区域波浪的传播变形问题时,精确度不高。缓坡方程模型仅适用于坡度变化较缓情况,对于波浪非线性、反射等因素考虑不足,不适用于近岸地形复杂和波浪非线性强的情况。而Boussinesq方程兼具色散型和非线性,使其不但能考虑包括波浪传播过程中的反射、折射、绕射等因素,扩展后还可以包括波浪破碎及海岸动边界问题,在模拟近岸波浪的传播变形问题中显示出巨大的优势[9-10]。在这类模型基础上建立考虑植被影响的数学模型是不错的选择,但目前基于Boussinesq方程建立的计算模型很少,而且主要集中在一维问题[9-10]。
综上所述,基于建立的水平二维、具备间断捕捉格式的Boussinesq波浪模型,在守恒形式的源项中引入由于刚性植被作用引起的拖曳阻力项,来考虑刚性植被区域波浪的传播变形,进行相关计算,并分别选取淹没、非淹没植被,以及植被覆盖水平二维复杂地形上的波浪传播变形算例进行验证。
1 数学模型
1.1守恒形式的二维Boussinesq水波方程

图1 坐标系统及变量定义Fig. 1 The sketch of cartesian coordinate and variable definition
在如图1所示的笛卡尔坐标系下,守恒形式的二维Boussinesq 水波方程[12-13]:
式中:下标x和y分别表示变量对x和y的偏导数,t表示变量对时间的偏导数。U为变量矢量,F(U)和G(U)分别代表x方向和y方向的通量矢量,S(U)表示源项,分别定义为:

其中,η为波面升高,h为静水深,d=η+h为当地总水深,g为重力加速度。P和Q分别为x和y方向的断面流量,即P=du,Q=dv(u和v分别为x和y方向的水深平均速度)。式(2)中U和V定义如下:
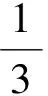

式(5)中Sb为海床坡度项,Sf为水底摩擦项,Sd为色散项,Sveg为植被作用引起的阻力项,其中摩擦项τx和τy,可表示为[14]:
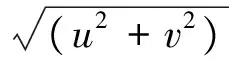
底摩擦系数f一般在0.001~0.01范围内,文中f为可调参数,具体值由相关的实验测量结果确定。φx和φy分别是x和y方向的色散项[12],定义为:


式中:B=1/15为色散性参数,该取值使控制方程适用于中等水深范围,即h0/L0<0.5(h0为特征波高,L0为特征波长)。τxveg和τyveg为由植被作用引起的阻力,具体求解公式见下节。
1.2植被阻力项
由于植被的存在,波浪经过植被区域时传播形态会发生变化。假定植被为刚性植被,则可忽略植被本身的运动,波浪经过植被区域受到的作用力主要有惯性力和拖曳阻力[15]。而植被的直径相对于波高来说很小,没有绕射影响,仅有黏性作用,因此忽略惯性力,只考虑拖曳阻力。将刚性植被简化为小圆柱体进行受力分析,植被引起的拖曳阻力可用莫里森公式表示[15],即:

式中:Cd是拖曳力系数,同流体特征以及植被特征密切相关,对数值结果有决定性影响,但迄今为止其取值没有统一认识,本文将其作为可调参数,通过实验结果进行率定,具体取值在算例中给出。Nv为区域中植被的密度,即植被均匀分布时单位面积的植株数,Av表示植被的迎水面积,定义为[9]:
法比因为将就枪伤的疼痛,僵着半边身体站在她对面。她对他讲这么多,让他有点尴尬,有点愧对不敢当,他又不是她的忏悔神甫,她也不是忏悔的教徒。对于常常独处的法比,把过多地了解他人底细看成负担,让他不适。或许叫玉墨的这个女人在做某种不祥的准备。
式中:bv和hv分别为植被的迎水宽度和植被的高度,bv取单株植被的直径Dv。

图2 出水和淹没植被的布置示意Fig. 2 Sketch of vegetation elements

图3 植被平面布置示意Fig. 3 Layout of vegetation
考虑到植被可以以出水和淹没两种方式出现(如图2所示),式(11)中的水平速度up确定如下[10]:
式中:Φ=Vs/V为植被自身与植被区域的体积比[10]。由上式可知,当植被出水时,up=u;当植被淹没时,up为等效速度。Vs的计算如图3所示,Vs=Nvπbv2hv/4为植被自身所占的体积,V为植被区域所占的空间,即等于水槽宽度、水深与植被区域长度的乘积。同理可得y方向的速度vp。
1.3数值格式和边界条件
在矩形网格系统上,采用具有总变差减小TVD(total variation diminishing)性质的有限体积-有限差分混合格式求解Boussinesq水波方程,利用高分辨率有限体积方法求解对流项而其他项仍然通过有限差分方法计算。由于充分利用了有限体积方法的守恒特性,模型克服了传统的、基于有限差分方法求解的同类模型存在的诸多缺陷,在稳定性、波浪破碎以及海岸动边界处理方面具有极大优势[13-14]。数值通量的计算采用兼具中心格式简单性和迎风格式精确性的新型数值格式——MUSTA格式[13],时间步长满足CFL稳定性条件限制。
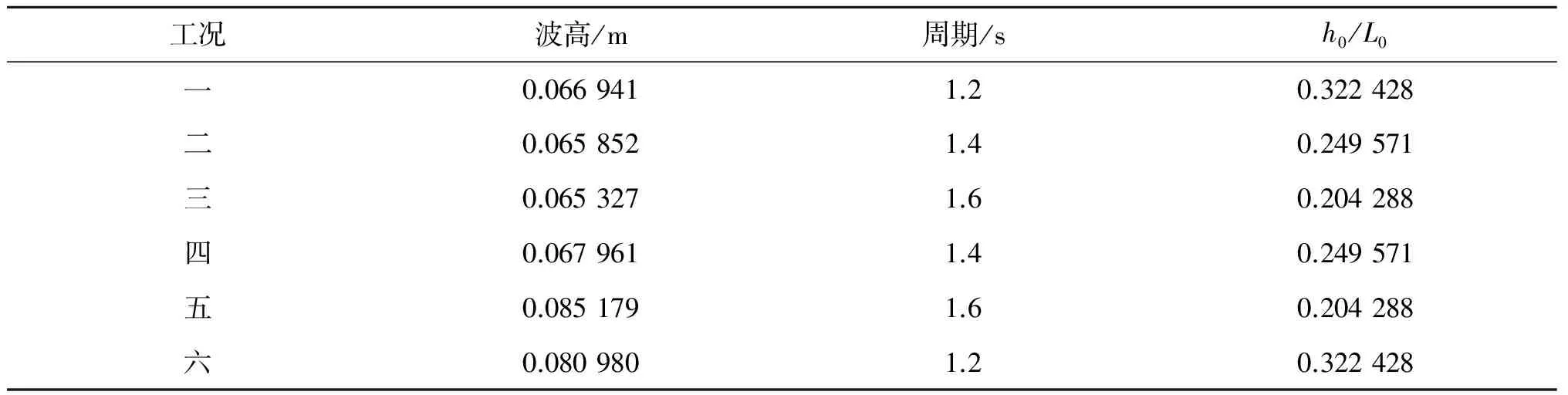
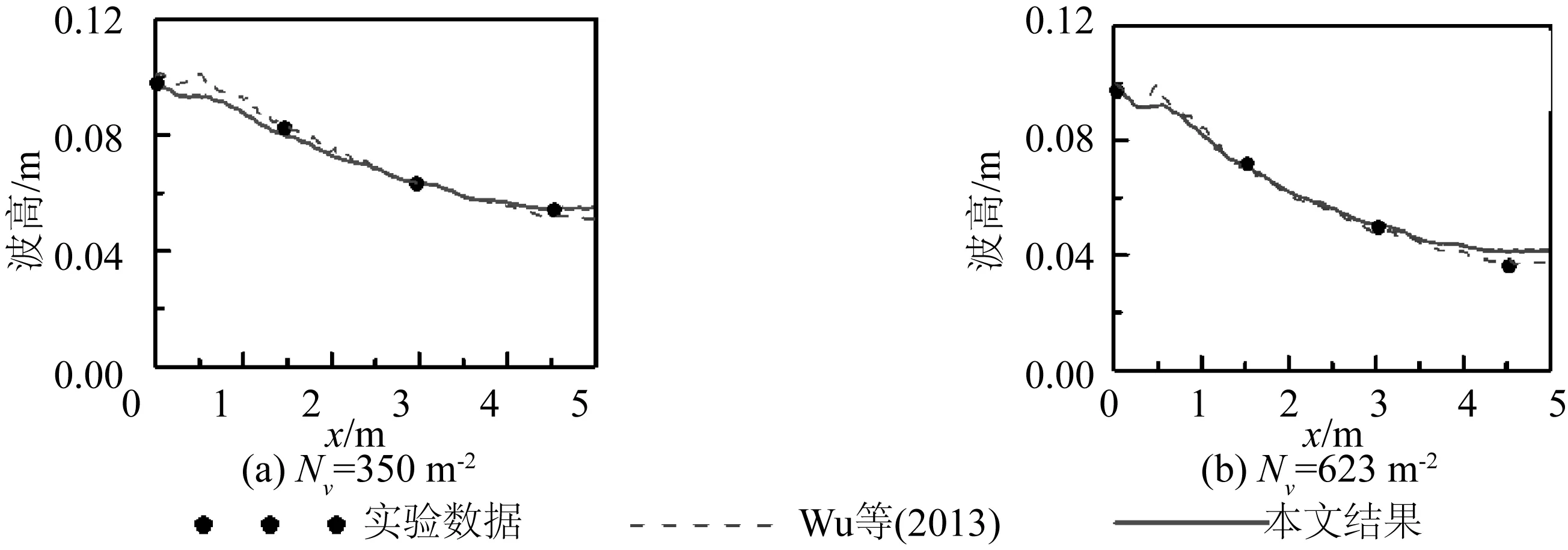
计算域两端设置为固壁边界,模型采用在质量方程中增加源项的方法产生波浪,同时视需要在计算域末端设置海绵吸收层吸收波浪[14]。当波面升高同水深比达到0.8时,认为波浪发生破碎,控制方程中的Boussinesq高阶非线性项和色散性不参与计算,方程退化为浅水非线性方程。对于海岸动边界,采用薄层水体法[13]处理, 即给定一极小水深值dmin,这里取0.000 1 m,若计算单元水深di,j>dmin(下标i和j分别为网格单元x和y方向的标记),判定单元为湿单元,反之,若di,j 为了验证所建立计算模型的精度和适用性,针对几个典型的植被区域波浪传播的物理模型实验进行数值模拟。 2.1淹没植被区域波浪的传播 该植被消浪实验是在密西西比国家泥沙实验室进行的[9],实验布置如图4所示,实验水槽尺寸为20.6 m×0.5 m×1.22 m(长×宽×高)。实验中用固定在床面的木质小圆柱体代表刚性植被,植被区域长Lv=3.66 m,植被密度为Nv=350 m-2,植被的高度和直径分别为hv=0.63 m和Dv=0.009 525 m。实验时取静水深h0为0.7 m,五个浪高仪分别布置在3 m、11 m、12.5 m、14 m和15.5 m处,水槽左侧为造波板,右侧为消波设备。实验所用波浪为规则波,对应的波要素如表1所示。 图4 波浪在植被区域传播变形的实验布置示意Fig. 4 Experimental sketch of the wave propagation in the vegetation area 工况波高/m周期/sh0/L0一0.0669411.20.322428二0.0658521.40.249571三0.0653271.60.204288四0.0679611.40.249571五0.0851791.60.204288六0.0809801.20.322428 数值水槽布置同物理模型实验水槽基本一致,如图5所示。计算域水槽长30 m,宽1.0 m。植被区域长度仍设为3.66 m,植被的密度、高度和直径均与实验设置一致。造波源距离左侧边界5 m,计算域的左右边界分别设置4 m宽的海绵层进行消浪。数值模拟的空间和时间步长分别取为Δx=Δy= 0.05 m和Δt=0.02 s,总模拟时间为60 s。拖曳力系数Cd经实验数据率定取值为3.5,底摩擦系数f取值0.005。由于不确定表1中波浪要素是否由G1浪高仪采集,计算时波浪要素的确定以波高计算结果同G2处实验数据吻合为准。 数值计算结果在图6中给出,其中x轴零点取在G2浪高仪位置处。如图6所示,当波浪在植被区域传播时,随着传播距离的增加,波高发生了不同程度的衰减,对于表1中6组不同的工况,本文模型的计算结果均和实验数据吻合良好,表明模型不但有足够的计算精度,也具有较好的适用性。对于该组物理模型实验,Kuiry 等[9]也采用Boussinesq类模型进行过数值模拟,计算结果也一并在图6中给出,可见其和本文计算结果基本一致,但存在一些细节差别。在G2处,Kuiry等的计算结果均偏低于实验数据,而本文计算时以G2处波高确定入射波浪要素,计算结果和实验数据吻合更好。对于所有工况,Kuiry等的计算结果均显示波浪在植被区域传播时会发生反射现象,入射波浪和反射波浪叠加导致波高产生波动,呈驻波形态。对于工况二~五,本文模型的计算结果也揭示同样的现象,但对于周期较小的工况一和六并不明显,这可能是由于计算时参数取值或数值水槽布置不同引起的。 图5 波浪在植被区域传播变形的数值模拟布置示意Fig. 5 Numerical sketch of the wave propagation in the vegetation area 图6 规则波经过淹没植被区域波高的变化Fig. 6 Variation of wave heights along the submerged vegetation area 2.2出水植被区域波浪的传播 仍然利用图5所示的数值水槽,取静水深h0为 0.5 m,植被区域的长度和位置不变,植被的高度hv为0.63 m,植被的直径Dv为0.009 4 m,拖曳力系数Cd经实验数据率定取值为4.5,底摩擦系数f取值为0.005。数值模拟的时间和空间步长分别取为Δx=Δy=0.05 m和Δt=0.02 s,总的模拟时间为60 s。选取两组不同初始波浪条件下植被密度值分别为350 m-2和623 m-2的工况[16],模拟出水情况下植被区域波浪的传播变形。 将本文Boussinesq模型的计算结果、Wu等[16]采用RANS类模型的模拟结果以及实验数据进行了对比,数值结果如图7、8所示。结果表明,与淹没情况类似,波高呈现下降趋势,而且相比植被淹没情况,出水情况下阻力较大,波高曲线变化较快,衰减剧烈。由图7和图8的分别对比发现,当入射波的波浪要素一定时,随着植被密度的增大,波高衰减速度加快,衰减幅度增大。本文的Boussinesq模型和Wu等的数值模拟在x=0处的数值结果和实验数据一致,两种数值模拟的曲线走势差别不大。图7、8中,整个数值模拟的结果和浪高仪处的实验结果吻合依然较好,由此可见模型同样适用于处理出水条件下波浪传播问题,适用性强。 图7 波高H=0.053 m、周期T=0.7 s的规则波经过出水植被区域波高的变化Fig. 7 Variation of wave heights along the emergent vegetation area for regular wave H=0.053 m and T=0.7 s 图8 波高H=0.10 m、周期T=1.0 s的规则波经过出水植被区域波高的变化Fig. 8 Variation of wave heights along the emergent vegetation area for regular wave H=0.10 m and T=1.0 s 2.3水平二维植被区域波浪的传播 Thuy等进行了一系列关于波浪在部分植被覆盖的斜坡上传播的实验[8, 17],具体的实验布置如9所示,实验水槽长15 m,宽4 m,静水水深0.44 m,地形的斜坡有不同的坡度,其中主要的坡度为1∶20.5。植被区域长1 m,沿x方向分布在10.36 m到11.36 m之间,植被区域的宽度为0.33 m,沿y方向分布在 0.07 m到0.40 m之间。沟槽的中心线在y=0.035 m处,植被区域的中心线在y=0.235 m处,在G6浪高仪处的沟槽和植被区域的中心线分别放置两个流速仪,植被区域和流速仪位置的平面布置如图10所示。具有水平二维特征的植被消浪物理模型实验非常少见,本文将其用于水平二维模型的验证。 数值模拟时,取计算域长25 m,宽0.4 m,造波板距离左侧边界5 m,计算域的左右边界分别设置4 m和5 m的海绵层进行消浪。初始状态的静水深为0.44 m,入射波的波高为0.032 m,周期为20 s。植被区域长度为1 m,与实验布置位置一致,植被的高度hv为0.5 m,植被的直径Dv为0.005 m,迎水宽度bv为0.005 m,植被的密度为Nv=2 200 m-2,数值模拟的空间步长分别为Δx=0.05 m和Δy=0.01 m,时间步长为Δt=0.02 s,总模拟时间为200 s。拖曳力系数Cd经实验数据率定取值为1.5,底摩擦系数f取值为0.005。 图9 Thuy等的实验布置示意Fig. 9 Experimental diagram of Thuy et al. 图10 植被区域和流速仪位置布置示意Fig. 10 The layout of the vegetation zone and the location of the velocity instrument 当波浪场稳定之后,计算得到不同流速仪处沿x方向的速度u的时间历程曲线,如图11所示。可以看出,当水流稳定后,两个位置处的速度时间历程曲线呈周期性变化,沟槽中心处流速的最大值约为40 cm/s,而植被区域中心处的最大值不足20 cm/s,显然,植被的阻力作用导致了植被区域的速度减小,消浪效果明显。数值模拟的速度历程曲线与实验结果的数据点吻合较好,进一步体现了模型处理水平二维复杂地形下部分植被覆盖区域波浪传播变形问题的优越性能。当植被区域宽度为0.4 m,即整个断面均布置有植被时,计算得植被区域的波高、波峰和波谷的比较情况,如图12所示,从图中可以看出,随着波浪的传播,水深逐渐变浅,波峰增大,波谷减小,波浪的非线性增强,在这个过程中,数值模拟与实验结果相比,无论是波峰、波谷还是波高,吻合依然很好,说明了模型处理相关水动力问题的能力,体现了模型的计算精度。 图11 速度的时间历程曲线Fig. 11 Time series of velocity 图12 整个断面均布置植被时的波高变化曲线Fig. 12 Variation of wave heights, crests and troughs through the cross section full of vegetation 基于已经建立的水平二维、具备间断捕捉能力的Boussinesq类波浪模型,建立了刚性植被区域波浪传播变形的计算模型,通过选取植被出水、淹没情况下不同入射波波高和波浪周期的算例进行模拟。数值结果表明,波浪在近岸植被区域传播时,波高发生不同程度的衰减,且波高衰减程度随着植被高度和植被密度的增加而增加。同时,选取水平二维部分植被覆盖的斜坡上波浪传播变形的算例进行模拟,波高和流速的计算结果同实验数据吻合良好,证明了所建立的数值模型对于复杂地形条件、刚性植被影响下的色散性波浪传播变形过程具有较高的计算精度,适用于开展刚性植被对波浪衰减作用的数值计算研究。 [1] 吉红香,黄本胜,邱秀云. 植被消波消浪研究综述[J]. 水利水运工程学报, 2005(1): 75-78.(JI Hongxiang, HUANG Bensheng, QIU Xiuyun. Summary of wave dissipation by the vegetation[J]. Hydro-Science and Engineering, 2005(1): 75-78.(in Chinese)) [2] 白玉川,杨建民,胡嵋,等. 植被消浪护岸模型实验研究[J]. 海洋工程, 2005, 23(3): 65-69.(BAI Yuchuan,YANG Jian min, HU Mei,et al. Model test of vegetation on the bank to attenuate waves and protect embankments[J]. The Ocean Engineering, 2005,23(3): 65-69.(in Chinese)) [3] 杨建民. 海岸带边坡防浪林消浪理论与实验研究[J]. 海洋通报, 2008, 27(2):16-21. (YANG Jianmin. Analytical solution and physical model test of wave protection forest on coastal zones[J].Marine Science Bulletin, 2008, 27(2):16-21.(in Chinese)) [4] 王瑞雪.非淹没刚性植物对波浪传播变形影响实验研究[D].长沙:长沙理工大学, 2012. (WANG Ruixue. Laboratory investigation on wave transformation through the emergent, rigid vegetation[D]. Changsha: Changsha University of Science & Technology, 2012.(in Chinese)) [5] 耿宝磊,高峰,张宇亭. 港口导堤植被消浪的试验研究[J]. 水运工程, 2014(7):51-57.(GENG Baolei, GAO Feng, ZHANG Yuhao. Experimental study on wave absorbing effect with vegetation on port jetty [J]. Port & Waterway Engineering, 2014(7):51-57.(in Chinese)) [6] MEI C C ,CHAN I C, LIU P L F,et al. Long waves through emergent costal vegetation[J]. Journal of Fluid Mechanics, 2011, 687:461-491. [7] NAOT D, NEZU I, NAKAGAWA H. Hydrodynamic behavior of partly vegetated open-channels[J]. Journal of Hydraulic Engineering, 1996, 122(11): 625-633. [8] THUY N B, TANIMOTO K, TANAKA N. Flow and potential force due to runup tsunami around a coastal forest with a gap-experiments and numerical simulations[J]. Science of Tsunami Hazards, 2010, 29(2): 43-69. [9] KUIRY S N, WU W, DING Y. A hybrid finite-volume/finite-difference scheme for one-dimensional Boussinesq equations to simulate wave attenuation due to vegetation[C]//Proc. of the World Environment &Water Resource Congress.2011: 2114-2124. [10] HUANG Z, YAO Y, SIM S Y ,et al. Interaction of solitary waves with emergent, rigid vegetation[J]. Ocean Engineering, 2011, 38(10): 1080-1088. [11] 唐军,沈永明,崔雷. 基于抛物型缓坡方程模拟近岸植被区波浪传播[J]. 海洋学报, 2011, 33(1):7-11.(TANG Jun, SHEN Yongming, CUI Lei. Modeling costal water wave propagation in vegetation field based on parabolic mild slope equation[J]. Acta Oceanologica Sinica, 2011, 33 (1): 7-11. (in Chinese)) [12] MADSEN P A , SORENSEN S R. A new form of the Boussinesq equations with improved linear dispersion characteristics. Part 2. A slowly-varying bathymetry[J]. Coastal Engineering, 1992, 18(3-4): 183-204. [13] FANG K Z, ZOU Z L, DONG P,et al. An efficient shock capturing algorithm to the extended Boussinesq wave equations[J]. Applied Ocean Research, 2013, 43:11-20. [14] 房克照,邹志利,孙家文,等. 扩展型Boussinesq水波方程的混合求解格式[J]. 水科学进展, 2013,24(5): 699-705. (FANG Kezhao, ZOU Zhili, SUN Jiawen ,et al. A hybrid numerical scheme for the extended Boussinesq equations[J]. Advances in Water Science, 2013, 24(5): 699-705. (in Chinese)) [15] MENDEZ F J, LOSADA I J. An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields [J]. Coastal Engineering, 2004, 51(2): 103-118. [16] WU W, ZHANG M, OZEREN Y, et al. Analysis of vegetation effect on waves using a vertical 2D RANS model[J]. Journal of Coastal Research, 2013, 29(2): 383-397. [17] THUY N B, TANIMOTO K, TANAKA N,et al. Effect of open gap in coastal forest on tsunami run-up- investigations by experiment and numerical simulation[J]. Ocean Engineering, 2009, 36(15-16): 1258-1269. A numerical model for coastal wave propagation in the rigid vegetation area WANG Lei1, FANG Kezhao1, YIN Jing2, SUN Jiawen2 (1. The State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China; 2. National Marine Environmental Monitoring Center, State Oceanic Administration, Dalian 116023, China) A numerical model for coastal wave propagation through the rigid vegetation area is developed based on the extended Boussinesq equations. Drag resistance force is introduced into the source term of momentum equations to consider rigid vegetation effect on wave attenuation. A hybrid finite-difference and finite-volume method is used to solve the governing equations. The resulting model has the advantages of strong-stability-preserving and shock-capturing and can effectively simulate wave transformation, breaking and moving shoreline in the coastal area. Typical numerical tests are conducted for model validation and the computed results are in good agreement with the experimental data, demonstrating the proposed model is applicable of predicting wave transformation in the coastal region covered with rigid vegetation. Boussinesq equations; rigid vegetation; wave attenuation; numerical simulation;wave propagation TV139.2; O353.2 A 10.16483/j.issn.1005-9865.2015.06.008 1005-9865(2015)06-062-08 2015-02-03 国家创新研究团队资助项目(51221961);国家海洋局海域管理技术重点实验室资助项目(201206) 王 磊(1988-),女,山东烟台人,博士生,从事海岸动力学方面的研究。E-mail: wangleiDUT@163.com2 模型验证








3 结 语

