基于季节性分解的时间序列在主变压器缺陷率预测中的应用
李勋,张宏钊,姚森敬,黄荣辉,刘顺桂,吕启深,张林
(深圳供电局有限公司,广东深圳 518048)
基于季节性分解的时间序列在主变压器缺陷率预测中的应用
李勋,张宏钊,姚森敬,黄荣辉,刘顺桂,吕启深,张林
(深圳供电局有限公司,广东深圳518048)
针对主变压器缺陷率序列具有的非线性和非平稳性特点,以及主变压器缺陷发生具有季节性的特征,提出将主变压器缺陷率序列进行季节性分解和时间序列ARIMA预测相结合对主变缺陷率进行预测,以探寻较为有效的主变压器缺陷率的预测方法。首先,对原始序列进行预处理,将其分解为一系列不同的模式分量,这样能够突出原始主变缺陷率序列的局部特征信息;然后,分析各分量,根据其变化规律,采用时间序列法建立相应的模型并进行预测,这样既简化了建立的模型又降低了不同分量间的干涉和耦合;最后将各分量的预测值叠加得到缺陷率的预测值。算例结果表明,该方法具有较好的预测效果。
主变压器;缺陷率;季节性分解;时间序列;自回归积分滑动平均模型;预测
主变压器作为电力系统中的重要设备,其可靠运行关系到整个电网的安全。主变压器一旦发生故障,将会导致巨大的经济损失和社会影响。由于变压器结构复杂,长时间带负荷运行,不可避免地会有各种缺陷的发生。并且,随着电网规模的扩大,变压器等主设备的消缺工作将耗费大量人力物力。对缺陷情况进行深度挖掘,科学有效地预测变压器缺陷发生概率,及时制定有针对性的措施,合理安排运维力量,可为设备运维管理提供参考,对保障设备安全有着重要意义[1-6]。
目前,数据预测方法主要分为3类:
1)传统数学模型法。如回归分析法[7],适合规则变化数列的预测。
2)非线性模型法。以人工神经网络[8]、模糊神经网络[9]等为代表,适合非常规变化数列的预测。
3)以结构为主的模型法。如小波分析法[10]等,适合多尺度但数列关系简单的预测。另外,也有研究者将上述方法结合起来进行数据预测[11]。
变压器缺陷的发生与设备质量、监造水平、安装工艺、运维措施、环境因素、气候影响等有关。缺陷数据具有较强随机性,同时包含着丰富的特征信息。通过对缺陷原始序列进行预处理,将不同特征信息分离开来,可降低建模难度及提高缺陷率的预测精度。本文结合季节性分解与时间序列方法对某地区主变压器缺陷率数据进行分析。首先,对主变压器缺陷率数据进行季节性分解,得到季节性因素项、趋势和循环项、随机波动项共3个序列;然后采用时间序列方法对各序列分别建模与预测;最后将各序列的预测值叠加,得到主变压器缺陷率的预测值。实际算例表明,本文方法能降低数据预测的建模难度,预测结果较传统时间序列方法更为准确。
1 季节性分解和时间序列预测理论
1.1季节性分解
季节性分解往往用于经济领域中与季节强相关的分析中,能够充分体现季节因素在数据中的影响作用[12-13]。由季节性分解所得的基本序列可突出数据的局部特征,在具有季节性特征的数据处理中有较好的效果。近年来,有研究人员将季节性分解用于电力需求预测,取得了一定的成果[14]。一般而言,季节性波动序列具有长期趋势性和季节性特征。长期趋势表现为持续上升或下降或平衡的总变化趋势,其变化特征可能为线性或非线性。季节性特征则是受气候等因素的影响,以一年为周期随着自然季节的推移而呈现出季节性的数据变化[15]。
本文所采用的季节性分解法为美国商务部人口普查局研究开发的X-11季节调整法。该方法基于移动平均法,分为乘法模型和加法模型[16]。本文采用的是加法模型,步骤概述如下:通过n次中心化移动平均法计算得到估计的趋势线项TC(n)t和季节不规则项SI(n)t,再通过“3×3”和“3×5”Henderson移动平均法计算得到估计的季节项以及季节调整后的值TCI(n)t。迭代2后,可得到季节性分解的各个分量。
季节性因素项:
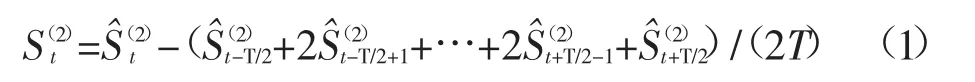
趋势和循环项:

随机波动项:

图1为一组具有明显季节性变化的序列数据,经季节性分解后得到图2各分量。
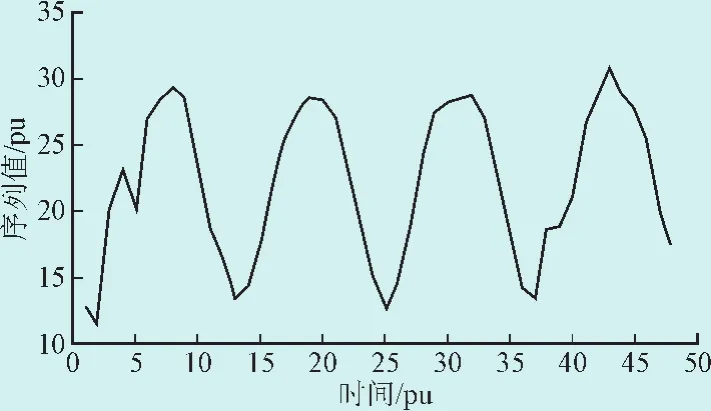
图1 季节性序列数据Fig.1 Seasonal data

图2 季节性数据分解的各分量Fig.2 Each component of the seasonal data decomposition
图2(a)显示该序列具有明显季节周期性,图2(b)显示该序列的整体变化趋势是上升增加的。季节性分解算法的引入证实了该序列数据受季节性气候变化影响显著。
1.2时间序列预测法
时间序列法是一种定量预测法,在统计学中作为一种常用的预测手段已被广泛应用。时间序列模型主要包括自回归模型(auto-regressive model,AR)、移动平均模型(moving average model,MA)、自回归移动平均模型(auto-regressive and moving average model,ARMA)、差分自回归移动平均模型(autoregressive integrated moving average model,ARIMA)等[17-20]。
本文采用ARIMA模型,该模型是建立在马尔可夫随机过程上,具有回归分析与移动平均的优点,是一种精度较高的短期预测方法,已在市场预测、经济预测、气象预测、电力负荷预测等领域有相关应用。
定义:设d是非负整数,样本数据{Xt,t=0,1,2,…,N}是ARIMA(p,d,q)序列,有:
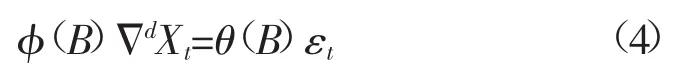

ARIMA模型预测的基本程序如下[20-21]:
1)根据时间序列的散点图、自相关函数和偏自相关函数图识别其平稳性;
2)对非平稳序列进行平稳化处理,根据处理后的数据自相关图和偏自相关图,建立相应模型,确定p和q;
3)参数估计,检验是否具有统计意义;
4)假设检验,判断残差序列是否为白噪声序列;
5)利用已通过检验的模型进行数据预测。
2 变压器缺陷率季节性分解的时间序列模型
2.1模型可行性分析
由于产品质量、运行工况及维护水平的差异,各变压器的健康状态、老化程度均存在一定的差异。变压器缺陷与家族缺陷、气候、负荷变化等密切相关,具有明显的季节性特征[22]。变压器产生缺陷原因大致可分为3类:
1)变压器所处地区具有季节性变化规律。另外,变压器各季节所承担的负荷具有一定规律,如夏季为用电高峰,变压器负荷明显要高于其他季节(即变压器缺陷原因的季节性因素项)。
2)随着城市建设的发展及用电需求的增加,变压器数量也随之增加,且随着运行时间的加长,变压器在热、电、机械等综合作用下,发生缺陷的数量亦有增加的趋势(即变压器缺陷原因的趋势和循环项)。
3)主变在运行过程中因操作不当、检修维护不当、外力破坏等原因引起的缺陷,具有不确定性(即变压器缺陷原因的随机波动项)。
综上,主变压器缺陷率数据规律符合季节性分解理论。另外,由统计学原理,数据样本量的增加可增加预测精度,本文涉及的主变压器缺陷率数据相对来说属于小样本数据,但季节性分解理论在小样本分析中与模糊集理论、神经网络等算法相比具有优越性[22]。
2.2算法模型结构
本文将在季节性分解的基础上结合时间序列分析,建立了一个新的预测模型,如图3所示。图中SD为季节性分解单元,Ci为分解后得到的第i个分解分量,ARIMAi为建立的第i个分解分量序列的预测模型,SUM为预测合成单元。

图3 预测模型Fig.3 Prediction Model
2.3算法
给定一个时间序列{X(t),t=1,2,3,…,N},N为主变压器缺陷数样本的总数。
第一步,将原始时间序列通过季节性分解成Ci。
第二步,对分解得到的各个分量进行时间序列分析,建立ARIMA(p,d,q)模型。本文选择Box-Jenkins法进行时间序列的分析建模,首先根据序列的平稳化过程确定d值,再根据平稳化序列的自相关函数和偏自相关函数图形并采用贝叶斯信息准则(Bayesian information criterions,BIC)进行定阶,选择出最合适的p,q值[23],如图4所示。
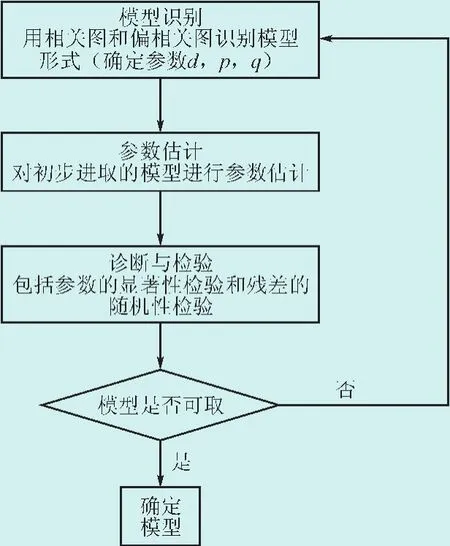
图4 ARIMA模型的确定Fig.4 Determination of the ARIMA model
第三步,根据第二步确定的ARIMA模型,对每个分量进行预测。例如,对第k个分量的预测如式(7)所示。
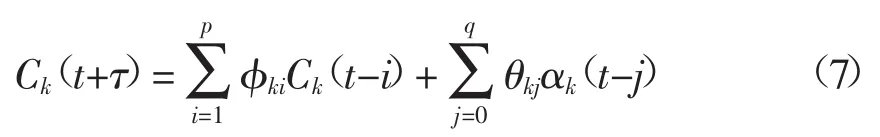
式中:τ为预测步长;φki为自回归参数;θkj为滑动平均参数。
第四步,将每个分量的预测值叠加,得到对原始缺陷数时间序列的预测结果,即式(8)。
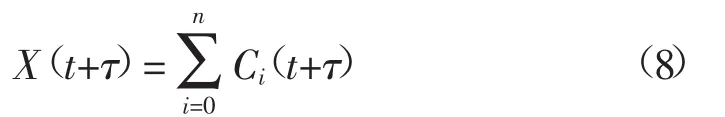
3 算例及结果分析
以某市的实测缺陷率为例,对本文所提算法进行验证。图5为某市2009年1月至2013年12连续60个月的实测缺陷率的序列,即原始缺陷率序列,共60个样本。
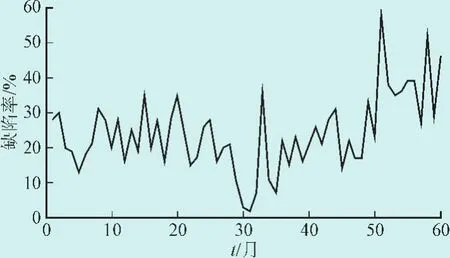
图5 样本缺陷率Fig.5 The number of defects sample time series
图5中原始序列波动较剧烈,但可以明显观察出,缺陷总数突出的月份集中体现在3月、9月。本文运用X-11季节调整法对原始缺陷率序列进行季节性因素分析,如表1所示。
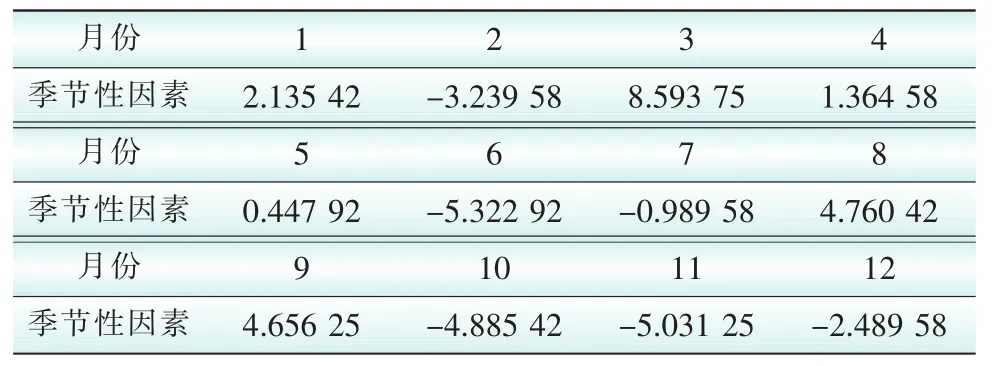
表1 季节性因素Tab.1 Seasonal factors
从表1可知,3月、8月、9月均为正值,并明显高于其他月份,其意义在于这3个月受季节影响因素较大;相反,6月、10月、11月等负值受季节影响因素小,证明缺陷的发生确实和季节有密切的相关性。
将2014年1月和2014年2月的缺陷率(样本点61-62)作为预测样本,按照3.2节所述算法,依次利用最近的60点预测下个月的主变压器缺陷率。以第61个点为例,预测过程说明如下:
首先,将前60个主变缺陷率样本进行季节性分解,得到3个基本模式分量:季节性因素序列(C1)、序列趋势和循环成分(C2)、随机波动序列(C3),如图6所示。可知,C1和C2分量均具有明显变化规律,C3的变化具有一定的随机性。接着,对这些分量建立ARIMA预测模型。其中,C2分量进行2次差分后即可得到平稳序列,故d=2。对应的模型阶数、BIC、平稳的R2值列于表2。显然,ARIMA(2,2,4)模型的BIC值最小,R2值最大。
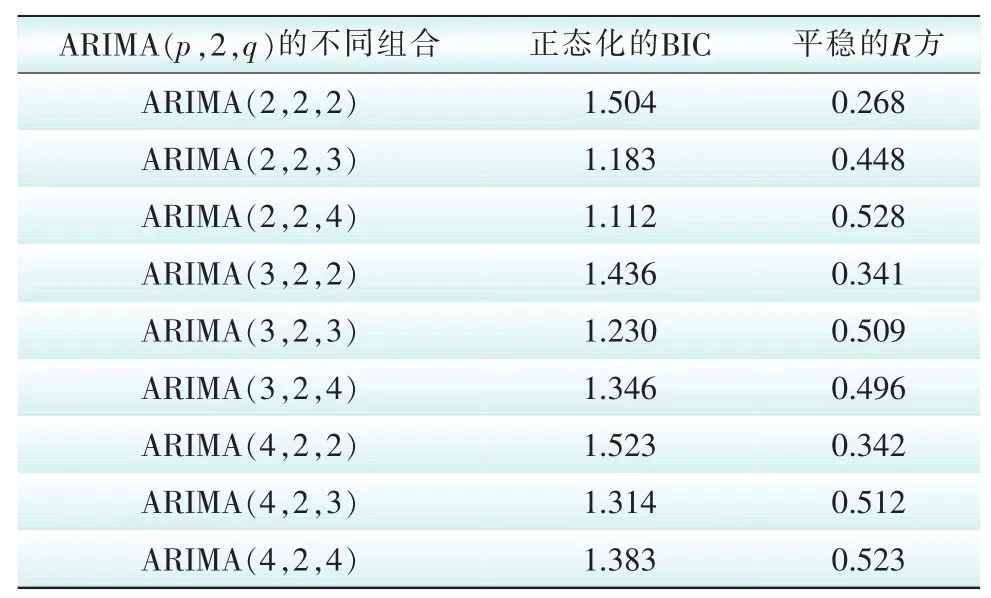
表2 ARIMA不同组合参数的比较Tab.2 ARIMA different combination parameter comparison
因此,在上述9种模型中,ARIMA(2,2,4)模型的拟合效果最佳,其他分量进行ARIMA建模过程与此类似。
最后,根据每个分量得到的相应模型进行预测,叠加得到预测的主变压器下月的缺陷率,预测结果和样本对比见图7。对图7中实际缺陷率和预测缺陷率曲线进行拟合度检验,得到差值均值0.45%,R方90.6%,可以看到2条曲线的拟合度较高。

图6 原始缺陷率序列季节性分解各分量图Fig.6 The original defects rate for the seasonal decomposition

图7 实际缺陷率和预测缺陷率的对比Fig.7 Comparison of the original defect rate and predicted defect rate
为了进一步考察本文算法的有效性,对原始缺陷率不进行季节性分解,而直接运用时间序列进行预测。对2种算法的预测结果和实际缺陷率进行比较,样本之后的第61~62个月(即2014年1月和2014年2月)逐个进行预测,得到预测结果如表3所示。
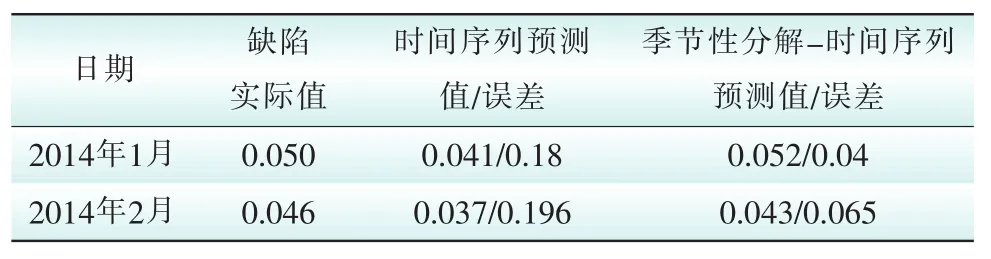
表3 预测值与实际值的比较Tab.3 Comparison of the predicted values and the actual value
由表3可知,2014年1月,本文所提方法的预测误差为4%,而纯时间序列方法的预测误差为18%;2014年2月,本文所提方法的预测误差为6.5%,而纯时间序列方法的预测误差为19.6%。较单纯的时间序列法,本文所提算法经过季节性分解处理,原缺陷数序列被分解为一系列变化较为平稳或有明显变化规律的分量,从而在很大程度上降低了不同特征信息之间的干涉和耦合,亦降低了建模难度;本文方法对不同分量建立不同的预测模型将更为准确,其预测精度也得到进一步提高。
另外,对各分量进行拟合时发现,随机波动序列分量的拟合效果欠佳,故认为本文方法的预测误差主要来源于对随机波动序列的预测误差。
4 结论
针对主变压器缺陷率序列的非线性和非平稳性,且缺陷的发生与季节有着明显的关系,本文提出一种基于季节性分解的时间序列法用于分析预测缺陷率。
1)运用季节性分解,对原始主变压器缺陷率序列进行了分解,使其具有一定的规律或趋势,从而简化了不同特征信息间干扰,同时也降低了每个分量的建模难度。
2)运用本文方法对某市实测主变压器缺陷率进行了测试,结果表明本文方法可提高主变压器缺陷率预测的精度,优于纯时间序列方法。
3)本文算法的误差主要来源于对随机波动序列的预测误差,下一步的研究重点是改进随机序列预测的方法。
[1]杨佳华,杨振睿,陆骏,等.基于风险概率的电力变压器设备风险评估技术研究[J].电网与清洁能源,2012(3):44-49.YANG Jiahua,YANG Zhenrui,LU Jun,et al.Risk assessment research on power transformers based on risk probability for power transformer[J].Power System and Clean Energy,2012(3):44-49(in Chinese).
[2]白翠粉,高文胜,金雷,等.基于3层贝叶斯网络的变压器综合故障诊断[J].高电压技术,2013,39(2):330-335.BAI Cuifen,GAO Wensheng,JIN Lei,et al.Integrated diagnosisoftransformerfaultsbased on three-layer bayesian network[J].High Voltage Engineering,2013,39(2):330-335(in Chinese).
[3]梁博渊,刘伟,杨欣桐.变压器健康状况评估与剩余寿命预测[J].电网与清洁能源,2010(11):37-43.LIANG Boyuan,LIU Wei,YANG Xintong.Transformer condition assessment and residual life prediction[J].Power System and Clean Energy,2010(11):37-43(in Chinese).
[4]熊浩,孙才新,张昀,等.电力变压器运行状态的灰色层次评估模型[J].电力系统自动化,2007,31(7):55-60.XIONG Hao,SUN Caixin,ZHANG Yun,et al.A hierarchical greyevaluation model for operation condition of power transformers[J].Automation of Electric Power Systems,2007,31(7):55-60(in Chinese).
[5]林朝晖,张彼德.基于BP神经网络的油浸式变压器寿命预测[J].高压电器,2010(4):84-87.LIN Zhaohui,ZHANG Bide.A prediction of the oil-filled transformer based on BP neural networks[J].High Voltage Apparatus,2010(4):84-87(in Chinese).
[6]林喆,兰生,张宇航.基于广义回归神经网络的油纸绝缘变压器的寿命预测[J].高压电器,2015(2):125-130.LIN Zhe,LAN Sheng,ZHANG Yuhang.Life prediction of oil paper insulation of transformer based on GRNN neural network[J].High Voltage Apparatus,2015(2):125-130(in Chinese).
[7]杨丽徙,张永锋,许向伟,等.半参数回归分析法在电力负荷预测中的应用[J].郑州大学学报:工学版,2010,31(3):29-32.YANG Lixi,ZHANG Yongfeng,XU Xiangwei,et al.Application of semi-parametric regression analysis method in electric power load forecasting[J].Journal of Zhengzhou University:Engineering Science,2010,31(3):29-32(in Chinese).
[8]王越,卫志农,吴佳佳.人工神经网络预测技术在微网运行中的应用[J].电力系统及其自动化学报,2012,24(2):83-89.WANG Yue,WEI Zhinong,WU Jiajia.Application of ANN prediction technology in microgrid operation[J].Proceedings of the Chinese Society of Universities for Electric Power System and its Automation,2012,24(2):83-89(in Chinese).
[9]宋志杰,王健.模糊聚类和LM算法改进BP神经网络的变压器故障诊断[J].高压电器,2013(5):54-59.SONG Zhijie,WANG Jian.Transformer fault diagnosis based on BP neural network optimized by fuzzy clustering and LM algorithm[J].High Voltage Apparatus,2013(5):54-59(in Chinese).
[10]浦星材,沈晓风,张清扬,等.基于偏最小二乘法的支持向量机短期负荷预测[J].电网与清洁能源,2011(10):32-35.PU Xingcai,SHEN Xiaofeng,ZHANG Qingyang,et al.Short team load forecasting based on partial least square SVM[J].Power System and Clean Energy,2011(10):32-35(in Chinese).
[11]程加堂,熊伟,段志梅,等.灰色神经网络在变压器故障诊断中的应用[J].高压电器,2010(8):56-58.CHENG Jiatang,XIONG Wei,DUAN Zhimei,et al.Application of gray neural network to fault diagnosis of transformer[J].High Voltage Apparatus,2010(8):56-58(in Chinese).
[12]潘泽清.时间序列季节调整的必要性、方法以及春节效应的调整[J].财政研究,2013(5):29-33.PAN Zeqing.The necessity to adjust the time series seasonal adjustment methods and effects of Chinese New Year[J].Public Finance Research,2013(5):29-33(in Chinese).
[13]赵安平,王大山,肖金科,等.蔬菜价格时间序列的分解与分析——基于北京市2002-2012年数据[J].华中农业大学学报:社会科学版,2014,109(1):49-53.ZHAO Anping,WANG Dashan,XIAO Jinke,et al.Time series decomposition and analysis of vegetable prices——based on data of Beijing from 2002 to 2012[J].Journal of Huazhong Agricultural University:Social Sciences Edition,2014,109(1):49-53(in Chinese).
[14]WEI Liyao.Using seasonal time series analysis to predict China’s demand of electricity[C]//2013 Fifth International Conference on Computational and Information Sciences.Shiyan,China:IEEE,2013:76-79.
[15]张锋利,陈文献,贾海英.支持向量机和BP神经网络在水轮发电机轴承故障诊断中的应用[J].电网与清洁能源,2013(4):62-66.ZHANG Fengli,CHEN Wenxian,JIA Haiying.Application of support vector machines and BP neural network in the rolling bearing of hydraulic turbine generator fault diagnosis[J].Power System and Clean Energy,2013(4):62-66(in Chinese).
[16]王亮红.基于时间序列分解技术的电力负荷预测乘积模型[J].东北电力大学学报,2013,33(6):45-47.WANG Lianghong.Product model for load forecasting based on decomposition technique in time series[J].Journal of Northeast China Institute of Electric Power Engineering,2013,33(6):45-47(in Chinese).
[17]张林,罗晓初,徐瑞林,等.基于时间序列的电力负荷预测新算法研究[J].电网技术,2006,30(S2):595-599.ZHANG Lin,LUO Xiaochu,XU Ruilin,et al.The new electric power load forecasting algorithm based on time series research[J].Power System Technology,2006,30(S2):595-599(in Chinese).
[18]黄磊,舒杰,姜桂秀,等.基于多维时间序列局部支持向量回归的微网光伏发电预测[J].电力系统自动化,2014,38(5):19-24.HUANG Lei,SHU Jie,JIANG Guixiu,et al.Photovoltaic generation forecast based on multidimensional time-series and localsupportvectorregression in microgrids[J].Automation of Electric Power Systems,2014,38(5):19-24(in Chinese).
[19]王燕编.应用时间序列分析[M].北京:中国人民大学出版社,2008:34-97.
[20]牛丽肖,王正方,臧传治,等.一种基于小波变换和ARIMA的短期电价混合预测模型[J].计算机应用研究,2014,31(3):688-691.NIU Lixiao,WANG Zhengfang,ZANG Chuanzhi,et al.Hybrid model based on wavelet transform and ARIMA for short-term electricityprice forecasting[J].Application Research of Computers,2014,31(3):688-691(in Chinese).
[21]麻常辉,冯江霞,蒋哲,等.基于时间序列和神经网络法的风电功率预测[J].山东大学学报:工学版,2014,41(1):85-89.MA Changhui,FENG Jiangxia,JIANG Zhe,et al.Wind power prediction based on time-series and BP-ANN[J].Journal of Shandong University:Engineering Science,2014,41(1):85-89(in Chinese).
[22]刘剑,刘开培,周仕杰,等.基于LS-SVM的变压器最优维护周期研究[J].中国电机工程学报,2012,32(22):94-103.LIU Jian,LIU Kaipei,ZHOU Shijie,et al.Research on optimal transformer maintenance scheme based on LSSVM[J].Proceedings of the CSEE,2012,32(22):94-103(in Chinese).
[23]栗然,王粤,曹磊.基于Box-Cox变换的风电场短期风速预测模型[J].现代电力,2008,25(4):35-39.LI Ran,WANG Yue,CAO Lei.Short term wind speed forecastingmodelforwind farm based on Box-Cox transformation[J].Modern Electric Power,2008,25(4):35-39(in Chinese).
Application of the Time Series Based on the Seasonal Decomposition in the Main Transformer’s Defect Rate Prediction
LI Xun,ZHANG Hongzhao,YAO Senjing,HUANG Ronghui,LIU Shungui,LÜ Qishen,ZHANG Lin
(Shenzhen Power Supply Co.,Ltd.,Shenzhen 518048,Guangdong,China)
Aiming at the nonlinear and non-stationary characteristics of the main transformer defect rate series and the seasonal characteristics of the occurrence of the main transformer defects,this paper proposes that the defect rate of the main transformer be predict by combining the seasonal decomposition of the main transformer defect rate series and timeseries ARIMA prediction to explore more effective defect data.First of all,the original series is pre-processed,and it is broken into a series of different model components,which can highlight the local feature information of the original main transformer defect rate series;Secondly,each component is analyzed and according to its change law,the mathematical model is set up using time series method and prediction is made.This method can not only simplify the model built but also reduce the interference and the coupling between the different components.Finally the predicted value of each component is added up to obtain the predicted value of the defect rate.The numerical example results show that the proposed method has good prediction effect.
main transformer;defect rate;seasonal decomposition;time series;auto-regressive integrated moving average model(ARIMA);predict
1674-3814(2015)11-0019-07
TM762
A
2015-06-30。
李勋(1983—),男,工学博士,工程师,主要从事主网技术监督和电力新技术的研究工作。
(编辑冯露)
南方电网公司重点科技项目(2013科资0038)。
Project Supported by Key Research Project of China Southern Power Grid(20130038).

