基于威布尔分布的电气设备缺陷率模型参数分析

基于威布尔分布的电气设备缺陷率模型参数分析

赵建利1,孙祎1,柴林杰2,李培栋3,路艳巧1

(1.国网河北省电力公司电力科学研究院，石家庄050021；2.国网河北省电力公司经济技术研究院，石家庄050021；3.国网北京经济技术研究院，北京100052)

摘要：针对传统指数模型和多项式模型曲线拟合存在的缺点，引入威布尔模型描述电气设备缺陷率发展的2个阶段，应用Levenberg-Marquardt法对模型参数进行求解，确定更为科学可靠的缺陷率突增期,并通过主网电气设备缺陷率统计数据进行算例分析，对3种拟合方法进行对比，验证了威布尔模型拟合曲线的有效性，为技改资金的分配以及运维决策的制定提供科学依据。

关键词：威布尔分布；电气设备；缺陷率；参数分析

收稿日期：2014-12-15

作者简介：赵建利(1980-)，女，工程师，主要从事输变电设备资产全寿命周期管理、智能信息处理工作。

中图分类号：TM732

文献标志码：A

文章编号：1001-9898(2015)01-0005-04

Abstract:For the disadvantages of exponential model and polynomial model, the paper uses Weibull distribution to describe the two defect progress stages of electrical equipment,and applies Levenberg-Marquardt method for model parameters solution, so as to determine the uprush period of defect rate more scientifically and reliably.At last, an instance of statistical data of defect rate of electrical equipment of major power network is analyzed, and three polynomial methods are compared to validate the feasibility, and to take reference for capital distribution and strategies of operation.

Parameter Analysis of Defect Rate of Electrical Equipment Based on Weibull Distribution

Zhao Jianli1, Sun Yi1, Chai Linjie2, Li Peidong3, Lu Yanqiao1

(1. State Grid HeBei Electric Power Research Institute, Shijiazhuang 050021, China;2. State Grid Hebei Economic Research Institute, Shijiazhuang 050021, China;3. State Grid Beijing Economic Research Institute, Beijing 100052, China;)

Key words:Weibull distribution;electrical equipment;defect rate; parameter analysis

0引言

电气设备故障率是研究设备的剩余寿命、进行风险评估、指导制订状态检修方案的主要依据，目前主要的电气设备故障率模型有“基于健康状态的故障率模型”[1]、“基于全寿命状态的故障率模型”[2]和“混合故障率模型”[3]等。这些方法都是将设备状态值作为模型的健康指数，依赖于较为详尽的设备状态评价数据。然而由于状态检修管理刚刚起步，历史状态评价数据严重缺失，现场几乎很难提供设备故障与设备状态的关联数据，这使得前述研究方法所得到的设备故障率可信度极低。

设备缺陷是设备故障的一个重要诱因，经常发生缺陷的某类设备其发生故障的可能性极高。研究设备缺陷的发展规律，探究缺陷率与故障率的内在联系，都可为状态检修决策优化提供科学依据。另外各地区历年都有详尽的设备运行缺陷记录，这为后续的研究提供了丰富的数据源支撑。

1常用电气设备缺陷率拟合模型

电气设备的缺陷是指运行或备用的设备发生了威胁设备和人身安全、影响经济运行、降低健康水平、影响设备载荷能力或寿命以及造成电能质量不合格等异常现象需进行处理的内容。电气设备的缺陷多种多样，按照对电网运行的影响程度分为危急、严重和一般三类缺陷[4]。设备缺陷不等同于设备故障，但设备缺陷的发生率从一定程度反应了运行设备的健康水平，是设备发生故障的一个重要诱因。通过统计电气设备若干年运行过程中的缺陷记录，研究设备缺陷率随役龄的变化趋势，科学地预测设备缺陷率的突增期，对于有效制定状态检修决策、合理统筹运维技改经费分配方案等工作都有重要的科学意义。

对主要设备的缺陷发生率与设备的役龄建立线性关系。缺陷发生率的公式如下：

(1)

式中：φ(t)为某类资产役龄为t的设备发生的缺陷率。

大部分电气设备缺陷率随时间变化的曲线类似于故障率曲线，但通常只包含后2个时期，即早期的偶然缺陷期和设备役龄增加到某个值后的耗损缺陷期。常用的设备缺陷率变化趋势拟合方法有指数型曲线拟合[5]和多项式型曲线拟合[6]。

1.1　指数型曲线拟合

设给定原始时间序列{y(x),x=1,2,…，n}，若y与x的关系可通过式(2)形式近似表达，则称函数y(x)是对原始时间序列的指数型曲线拟合。

y(x)=ae-bx

(2)

式中：a为比例系数；b为曲率系数，其值可利用最小二乘法得到。过程如下：

对y=ae-bx两边取对数，得lny=lna-bx。令u=lny，A=lna，B=-b，则替换后的函数关系为u=u(x)=A+Bx，该直线方程的法方程为：

由此求解出A、B的值，再将A、B值还原为a、b值，即可确定式(2)所表征的指数模型。

用指数模型进行缺陷率曲线拟合，认为设备缺陷率会随着设备役龄的增加呈现指数级增长，这在描述设备早期的偶然缺陷期是不合理的。

1.2　多项式型曲线拟合

对于给定的一组数据：{(xi,yi),i=0，1,2,…，N}，构造M阶多项式y=f(x)=a0+a1x+a2x2+…+aMxM来拟合这N个数据点，从而对数据组进行模型描述。通过求式(3)的最小值可得到多项式系数a0，a1，…，aM。

(3)

ε(a0，a1，…，aM)对a0，a1，…，aM分别求偏导数得：

…

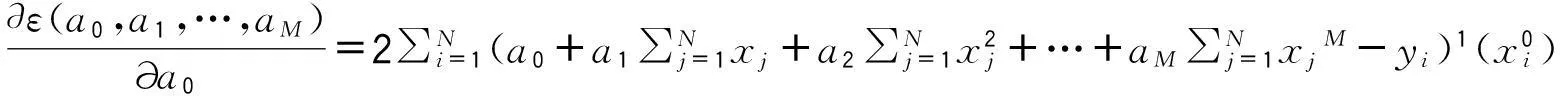
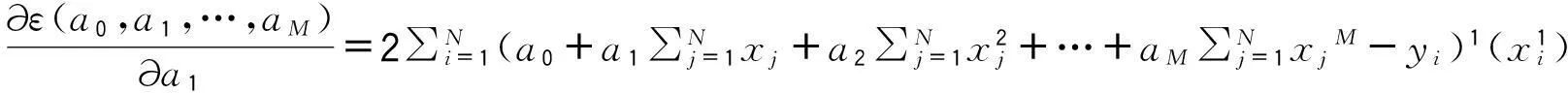
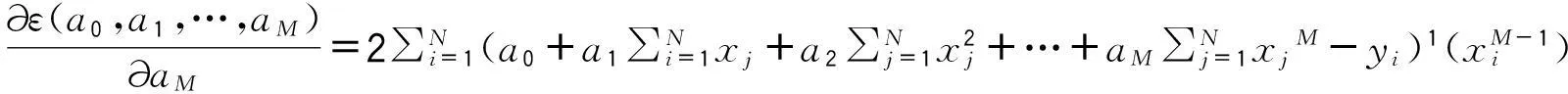
令偏导数为零，正规化后解出a0，a1，…aM便可求得拟合函数f(x) 。但用多项式进行电气设备缺陷率曲线拟合时会出现过零的情况，这与实际应用并不相符。

2基于威布尔分布的电气设备缺陷率模型参数拟合

2.1　基于威布尔分布的缺陷率曲线

以下将采用在数据拟合上极具弹性的威布尔分布[7]来描述缺陷率曲线的2个阶段。

基于威布尔分布的缺陷率函数为

(4)

式中：β为形状参数，描述曲线的开关；η为曲率参数，表示坐标尺度。当β=1时，缺陷率呈常数，可描述缺陷模型中的偶然缺陷期；当β>1 ，缺陷率呈现上升趋势，可描述缺陷模型中的耗损缺陷期。

通过对同一类型电气设备的历史缺陷率统计数据，可对基于威布尔分布的缺陷率曲线分段拟合，并求得各阶段的参数β和η。

2.2　基于Levenberg-Marquardt法的威布尔分布参数拟合

为了提高拟合精度，采用了Levenberg-Marquardt法[3](简称“LM法”)来求解电气设备的缺陷率函数。LM法在解决已知非线性关系式的参数估计问题方面较为有效，目前已广泛应用在负荷预测和设备状态预测[8-9]等领域。

设有N组按照时间顺序排列的电气设备缺陷率数据(t1，φ1)，(t2，φ2)，…，(tL，φL)，…，(tN，φN)，利用LM法进行威布尔模型中β和η参数估计的步骤如下：

(1)取原始数据中前L组做偶然缺陷阶段的曲线拟合，剩下N-L组做耗损缺陷期阶段的曲线拟合。

(2)设ti为第i组数据中自变量的值，参数β和η的初始迭代值为a(0)=(β(0),η(0))，将φ(ti，a) 在a(0)处按泰勒级数展开，并略去二次及以上的项得：

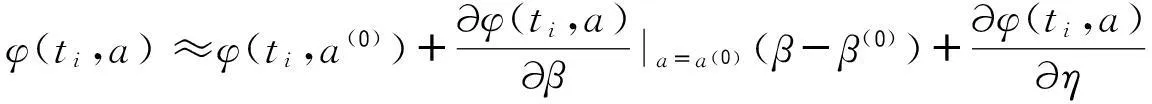
(5)

(4)为下文表述清晰，特定义以下变量，β和η的求解过程如图1。

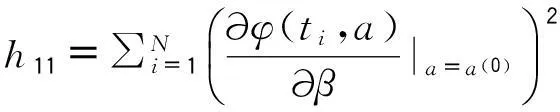
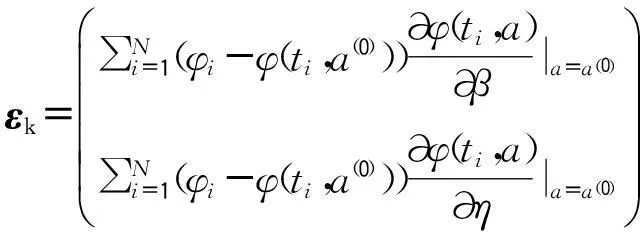
(5)通过式(4)计算得到设备偶然缺陷期函数φ(t)1和耗损缺陷期函数φ(t)2，利用式(6)计算2个阶段的最佳分界点L。

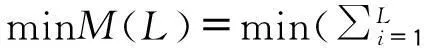
(6)

3算例分析

为验证此方法应用于实际工程的有效性，以华北某地区2013年度统计的主网电气设备缺陷率数据为例进行计算分析。主变压器、断路器、隔离开关和GIS的资产役龄与缺陷率统计数据见表1。

图1　用LM法进行威布尔模型中 β和 η参数求解过程

表12013年度主网主要电气设备缺陷率统计数据

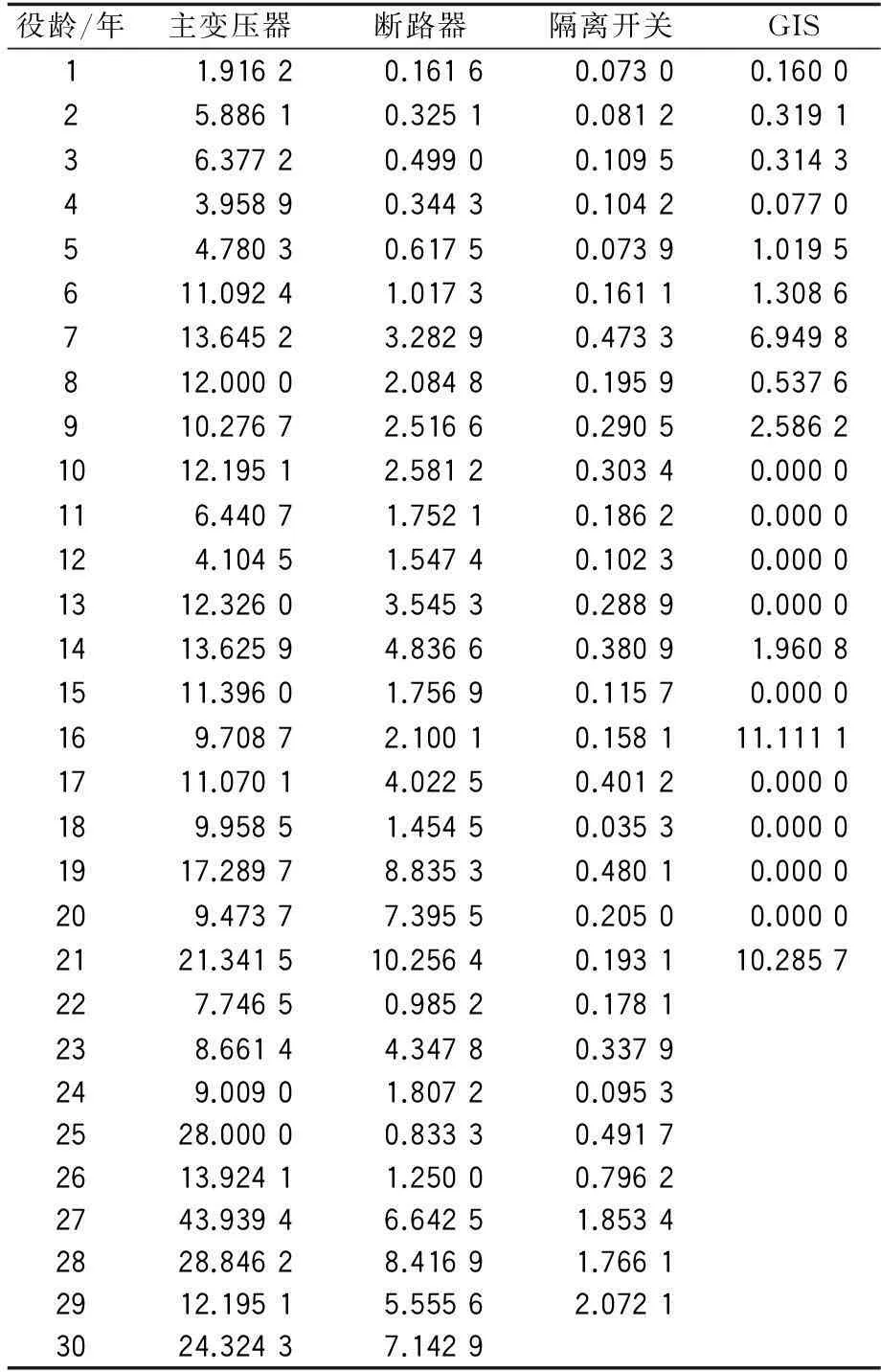
役龄/年主变压器断路器隔离开关GIS11.91620.16160.07300.160025.88610.32510.08120.319136.37720.49900.10950.314343.95890.34430.10420.077054.78030.61750.07391.0195611.09241.01730.16111.3086713.64523.28290.47336.9498812.00002.08480.19590.5376910.27672.51660.29052.58621012.19512.58120.30340.0000116.44071.75210.18620.0000124.10451.54740.10230.00001312.32603.54530.28890.00001413.62594.83660.38091.96081511.39601.75690.11570.0000169.70872.10010.158111.11111711.07014.02250.40120.0000189.95851.45450.03530.00001917.28978.83530.48010.0000209.47377.39550.20500.00002121.341510.25640.193110.2857227.74650.98520.1781238.66144.34780.3379249.00901.80720.09532528.00000.83330.49172613.92411.25000.79622743.93946.64251.85342828.84628.41691.76612912.19515.55562.07213024.32437.1429

通过2.2介绍的方法得出各设备威布尔分布的缺陷率参数见表2，根据式(6)得到各威布尔缺陷率函数的最优分界点L，对于给定缺陷统计数据分别绘制得到其指数型、多项式型及威布尔型拟合曲线，见图2。

表2缺陷率函数参数

缺陷阶段主变压器βη断路器βη隔离开关βηGISβη偶然缺陷期1.29020.54121.58022.04031.42308.99391.40112.9041耗损缺陷期3.12304.69013.02606.78995.290219.50435.491010.2893

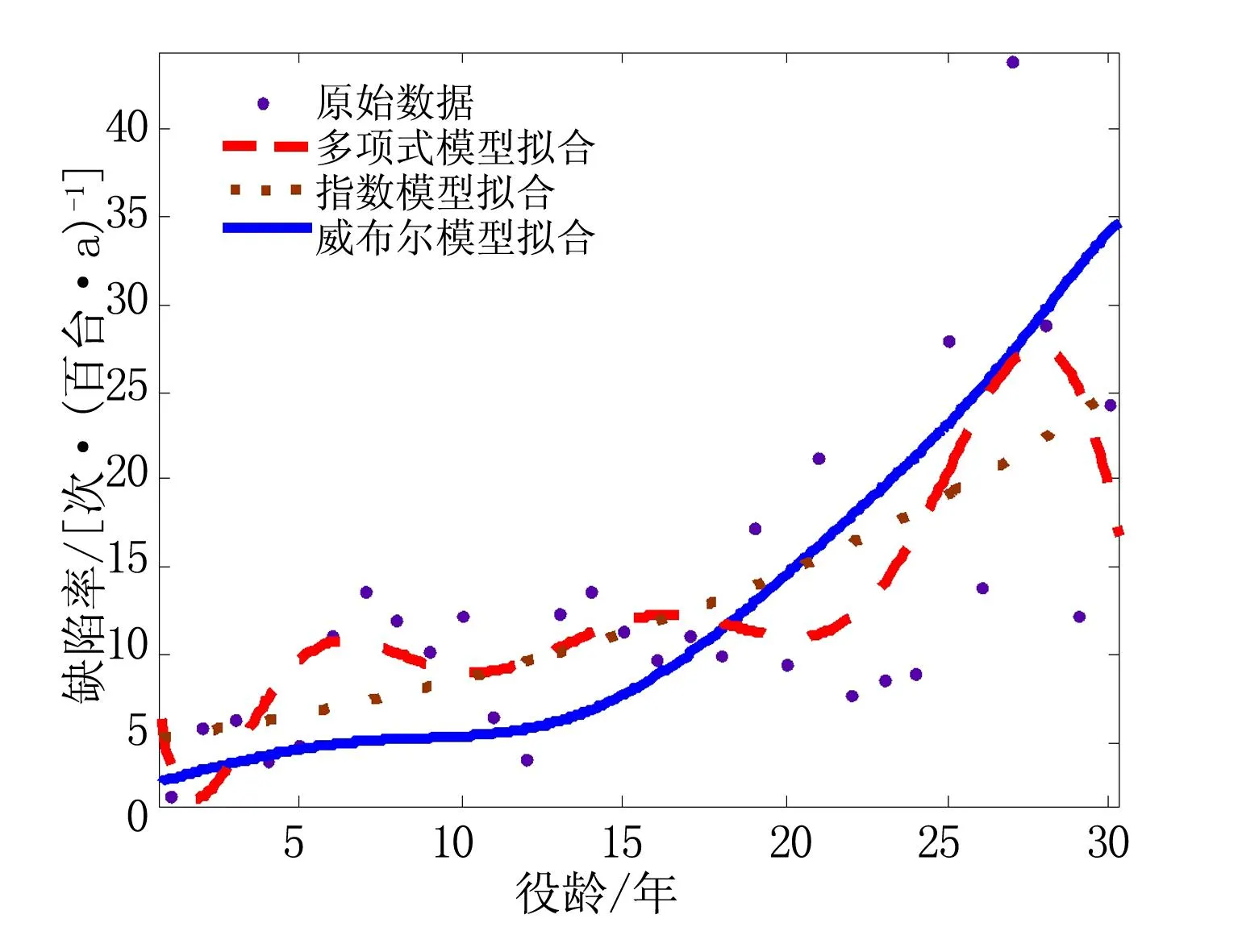
(a)　主变压器

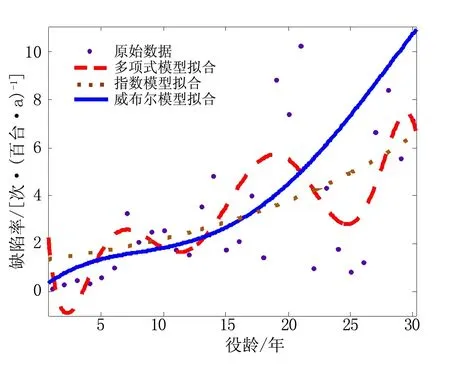
(b)　断路器

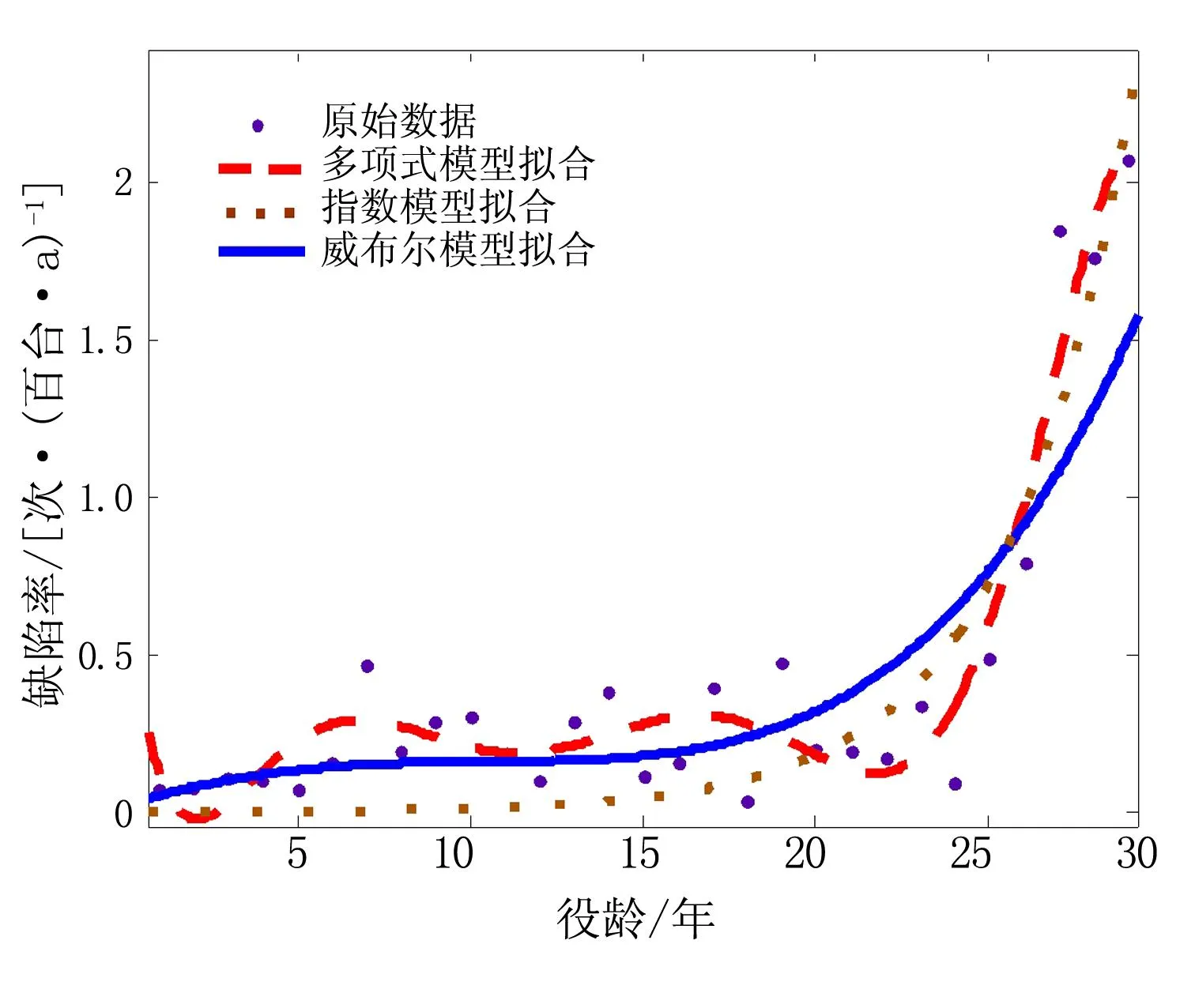
(c)　隔离开关

(d)　GIS

根据2013年的缺陷率统计数据，从计算结果及图2分析可知，主变压器、断路器、隔离开关和GIS的缺陷率突增役龄分别为15、16、20、15；从3种拟合模型的对比来看，指数模型拟合曲线的变化趋势较平缓，多项式模型拟合曲线波动较大，且会因为原始数据中存在较多零点数据时出现过零现象，而以上所研究的威布尔模型拟合曲线则弥补了前两种模型的缺点，更科学的呈现了电气设备缺陷役龄增加时的发展趋势，得到的缺陷率突增役龄更为可靠。

4结束语

在电网电气设备的运行过程中积累了大量的设备缺陷信息，如何从这些海量数据中发现设备缺陷发展规律从而指导设备运行维护策略制定一直是电网运维管理人员积极探索的内容。以上参考设备故障率研究取得的成果，用威布尔模型描述电气设备缺陷率发展的2个阶段，并利用LM法对模型参数进行求解，从而得到更为科学的缺陷突增期，为技改资金的分配以及运维决策的制定提供科学依据。

参考文献：

[1]潘乐真,张焰,俞国勤,等.状态检修决策中的电气设备故障率推算[J].电力自动化设备,2010,30(2):91-94.

[2]王一,何奔腾,王慧芳.基于全寿命状态的设备可靠性研究[J].电网技术,2011,35(8):207-211.

[3]冯管印,何川,丁坚勇,等.电气设备故障率演化推算综合算法[J].武汉大学学报(工学版),2014,47(2):244-249.

[4]Q/GDW 1906 - 2013,输变电一次设备缺陷分类标准[S].

[5]国振双,周申范,陈佼.指数模型建立方法[J].南京理工大学学报(自然科学版), 1994(3):74-78.

[6]王珏,伍立芬,邹永宁,等.Zernike矩边缘检测与多项式拟合的CT图像三维测量算法[J].仪器仪表学报,2012,33(2):442-449.

[7]张翔,宋子彤,杨致慧,等.一种基于负载率和设备检测信息的油浸式变压器故障率模型[J].电网技术,2013,37(4):1159-1165.

[8]王志勇,郭创新,曹一家.基于模糊粗糙集和神经网络的短期负荷预测方法[J].中国电机工程学报，2005,25(19):7-11.

[9]毛颖科,关志成,王黎明,等.基于BP人工神经网络的绝缘子泄露电流预测[J].中国电机工程学报，2007(27):7-12.

本文责任编辑：罗晓晓

下期要目

动态连续潮流与改进细菌觅食算法结合的静态电压稳定裕度计算方法

高压电动机故障引起的6 kV厂用电失电分析

基于舒适度的多变量混沌短期负荷预测