金属板中Lamb波波速与应力关系的实验研究∗

王军　韩庆邦

（1重庆第二师范学院数学与信息工程系重庆400067）（2河海大学物联网工程学院常州213022）

金属板中Lamb波波速与应力关系的实验研究∗

王军1†韩庆邦2

（1重庆第二师范学院数学与信息工程系重庆400067）（2河海大学物联网工程学院常州213022）

本文给出了金属板中Lamb波波速对同向应力变化率测量的装置，分析探讨了测量原理及误差，并对Lamb波的波速与应力关系进行了实验研究。结果表明Lamb波的波速对应力有较好的线性关系，Lamb波相速度对应力的变化率的实验值与理论值符合很好，可为Lamb波的应力测量提供实验依据。

静应力，Lamb波，频散方程频

1　引言

利用超声波技术检测应力的基本原理是基于材料的声弹效应，即施加在材料上的应力变化引起超声波传播速度的变化，变化的大小取决于超声波波型、传播方向、材料组织和应力状况等。声弹效应早在60年前就被人们发现并进行应用，但由于超声波的声弹效应是一种弱效应，应力引起的声速变化非常小，要测出这个变化，需要灵敏度和精度非常高的测量技术和仪器设备。另外材料结构和粗晶对超声波传播速度的影响，以及超声波传播速度对温度变化较敏感，因此利用超声波测量应力的发展非常缓慢，工业应用很少。尽管如此由于超声波所固有的特性，如穿透能力强、仪器设备简单、测量速度快、低成本等，利用超声波无损测量材料表面和内部的应力状况的潜力是显而易见的。

Hughes和Kelly［1-2］用有限形变的弹性理论方法来研究各向同性固体中的波速与附加的静应力的关系，文献［3］用同样的理论基于各向同性固体在正交静应力下可认为是正交各向异性体［4］的假设，推导出了金属板中Lamb波波速与静应力的关系，从而得出了Lamb波波速与应力变化率的关系，得出：对一定频率一定模态，Lamb波相速度对平行和垂直方向应力的变化率可近似看作常数这一结果。本文设计了Lamb波波速与应力变化率的实验测量装置，主要研究Lamb波与钢板和铝板中的同向应力关系，并将实验结果与理论值进行比较，验证这一结论。

2　Lamb波波速与薄板应力关系实验原理

图1是超声Lamb波实验测式系统，它主要由一个发射换能器、两个接收换能器、超声脉冲发生/接收器、数字示波器和万能试验机等组成。

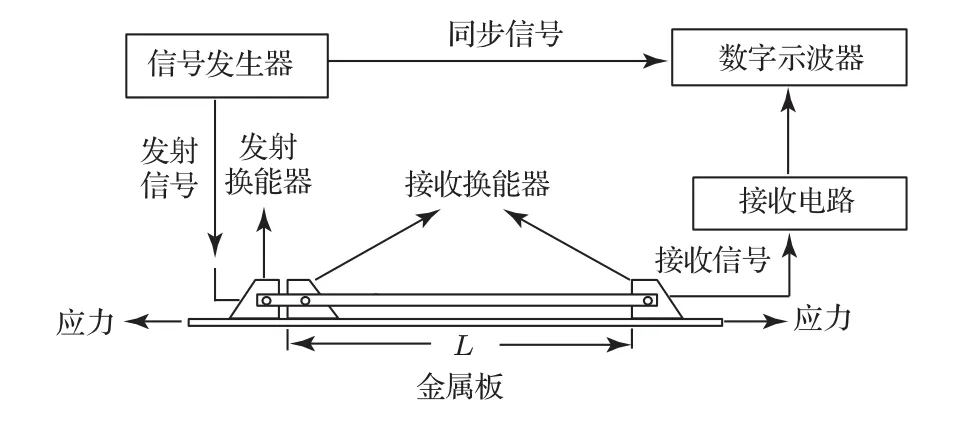
图1　Lamb波实验装置测量系统Fig.1 Experimental measuring system of Lamb wave

金属板被加工成矩形条状，夹在万能试验机上，通过计算机控制万能试验机对金属板加载指定大小的应力。发射和接收换能器为同型号的可变角纵波换能器，或固定角度的斜探头，将发射和接收换能器按图1所示沿应力方向放置在金属板的同侧，两个接收换能器的间距L保持固定，换能器与金属板之间用油作为超声耦合剂耦合。超声脉冲发生/接收器采用美国Panametrics公司的型号5052UA的超声分析仪，其发出的脉冲激励发射换能器产生纵波，同时发出一同步信号触发数字示波器，接收换能器接收的是经过金属板传播的Lamb波信号，通过接收电路预处理后传至数字示波器。为了减少随机噪声对结果的影响，数字示波器对采样进行多次平均。我们所采用的数字示波器是Tektronix的TDS1002型数字示波器，最大测时精度能达0.2 ns，图2是实测实验装置照片。

图2　实验装置Fig.2 Experimental device

实验中当应力加载改变ΔT（MPa）时，示波器中两个接收换能器的接收波形的高频载波随之移动，移动的间隔对应Lamb波在板中相速度传播时间的变化。定义Lamb波在相距L的两接收换能器间的传播时间的变化为Δt。在示波器选前探头波形中幅度最大的一个波周期，测出其周期，为了保证频率的一致，在后探头波形中选取相同周期的一个波，如铝板S0模式的小线段，其周期是1458 ns，采用过零点法读取这前后两个正弦波的声时改变，后探头声时的改变减前探头声时的改变就得出相距L得两接收换能器间的传播时间的变化Δt。注意：由于这里测量的是高频波的移动，不是波包的移动，故其声时的改变应是相速度改变引起的。

设在板中无应力时，Lamb波在相距L距离的传播时间为t0，加载应力ΔT后传播时间变为t0+Δt，则Lamb波的相速度为c=L/（t0+Δt），两边取微分，考虑到t0≫Δt得应力引起的Lamb波相速度改变

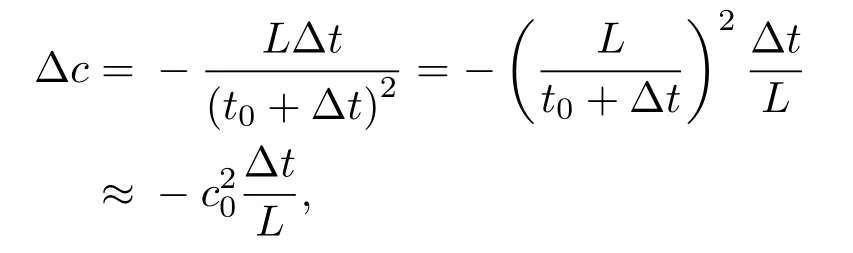
由此可得相速度对应力的变化率：

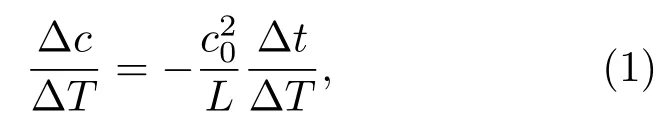
c0是没有应力时Lamb的速度，利用式（1）可以不直接测量Lamb波的相速度，而通过测量应力引起的声时改变Δt来表示声速对应力的变化率，避免了测量误差。

3　板中Lamb波相速度的测量误差分析

由（1）式可得相对误差：

由于应力加载是以数个106Pa，精度到100 Pa；L的长度是数量级10-1m，精度到5×10-4m；时间的变化Δt为数量级10 ns，精度为0.2 ns，因此相对误差的主要来源是由测时精度引起的，约10%左右。

此外实验中还有两个误差来源，一个是外界随机干扰信号，它造成过零点的左右摇摆不定，在实际测量中我们采用多次平均的方法来降低它的影响。另一个是系统自身的误差，它主要包括：两个接收探头中心频率的不一致产生的误差，如果测点是在声速对频厚积变化率较大的位置处，它的影响就变的很大了；同样的道理金属板厚度不均匀产生的误差也在同一量级内，以产生频厚积的改变约0.1 MHz·m，以1 mm铝板，频率2 MHz的A1模式的Lamb波为例，其相速度随频厚积的变化十分显著，2 MHz·mm的频厚积对应的相速度应力变化率是7.7×10-3km·s-1/MPa，2.1 MHz·mm的频厚积对应的相速度应力变化率是6.4×10-3km·s-1/MPa，改变了16.9%，因此测量中声速对频厚积变化敏感的范围内其频厚积变化引起的测量误差要大的多，这也是实验中对频率的选择要重点考虑的问题。至于拉应力的作用导致金属板厚的改变而引起的误差就很小了，如铝板用30 MPa的拉应力，根据泊松效应，将引起厚度为1.46×10-4相对改变，因此比起其它因素产生的误差，拉应力引起的误差可忽略。

由于NB的窄带特性，必须通过控制瞬时下行数据量，才能保证下行控制的及时性和有效性。下行控制的离散原则如下：

4　Lamb波波速与薄板应力关系实验结果

在我们前期的理论研究中，得到在一定的模态和频率，声速对应力的变化率是一常数的结论，本实验的目的就是验证这个结论。在实验中直接测量相速度是比较困难的，而且误差较大。这里我们采用测量应力引起的声时改变Δt来反映声速的变化。实验采用钢板和铝板两种材料，材料的参数为

钢板：长500 mm，宽40 mm，厚1.8 mm；铝板：长500 mm，宽40 mm，厚1 mm。

实验结果如下：

（1）Lamb波频率f=2.5 MHz，A3钢钢板厚h=1.8 mm，L=17.5 cm，Lamb波模式是A1模式，实测频率是2.550 MHz，测量的波形及结果如图3∼4所示。

图4　钢板后探头A1波形Fig.4A1mode waveform of second receiver in steel plate

根据上述的测量原理，得到的钢板中A1模式的Lamb波声速与应力关系如图5所示。可以看出声速随应力单调减小，拉应力与延时近似成直线关系。经过线性拟合，线性相关系数的平方为0.9699。由文献［3］得到的理论值为

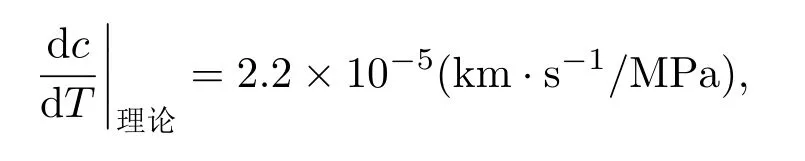
而得到的声速对应力的变化率

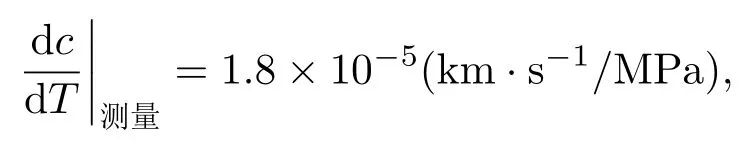
与理论值约有18%的相对误差。

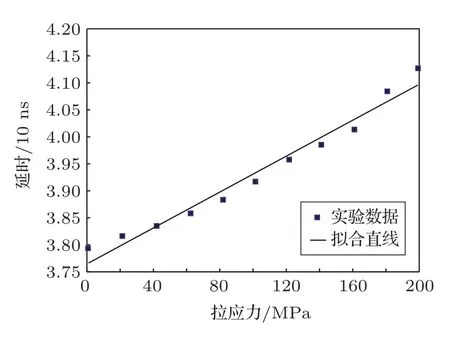
图5　钢板中A1模式的Lamb波相速度与应力关系Fig.5 Relationship curve of Lamb A1mode phase velocity and stress in steel plate

（2）Lamb波频率f=2 MHz，A3钢板厚h=1.8 mm，L=17.41 cm，Lamb波模式是S2模式，实测频率是2.083 MHz，测量波形及该模式下的Lamb波相速度与应力关系如图6∼8所示。

由文献［3］得出

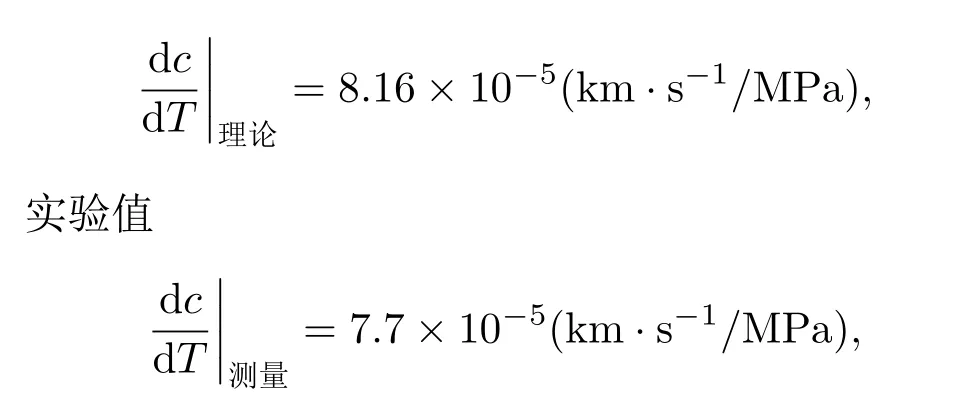
与理论值约有6.1%的相对误差。其拟合直线的线性相关系数的平方为0.9835。

（3）Lamb频率f=2 MHz，铝板厚h=1 mm，L=14.95 cm，Lamb波模式是A1模式，实测频率是2.083 MHz，测量波形及Lamb波相速度与应力关系如图9∼11所示。

图6　钢板前探头S2波形Fig.6 S2mode waveform of first receiver in steel plate

图7　钢板后探头S2波形Fig.7S2mode waveform of second receiver in steel plate

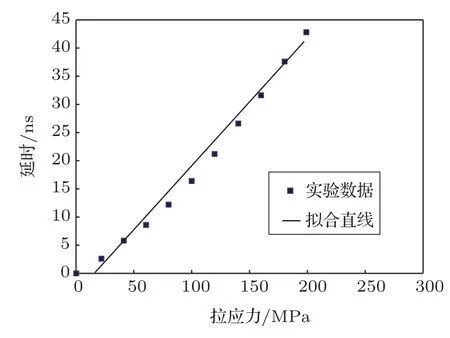
图8　钢板中S2模式的Lamb波相速度与应力关系Fig.8 Relationship curve of Lamb S2mode phase velocity and stress in steel plate

由文献［3］得出

与理论值约有18%的相对误差。其拟合直线的线性相关系数的平方为0.9556。

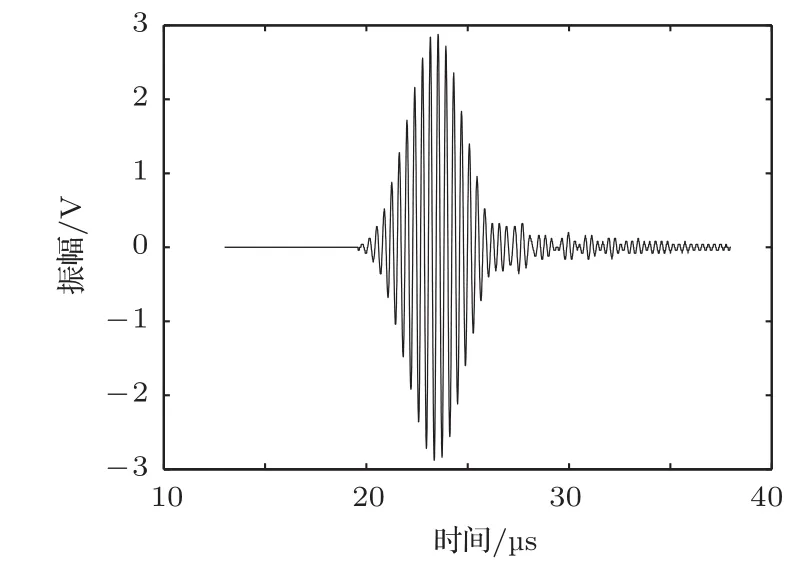
图9　铝板前探头A1波形Fig.9 A1mode waveform of first receiver in aluminum plate

图10　铝板后探头A1波形Fig.10 A1mode waveform of second receiver in aluminum plate

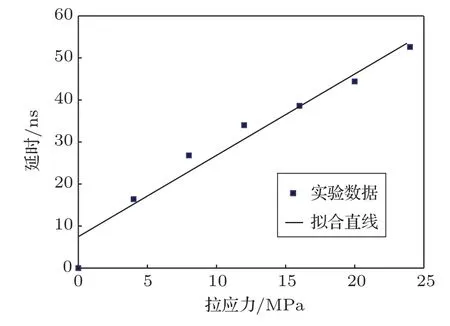
图11　铝板中A1模式的Lamb波相速度与应力关系Fig.11 Relationship curve of Lamb A1mode phase velocity and stress in aluminum plate

图12　铝板前探头S0波形Fig.12 S0mode waveform of first receiver in aluminum plate

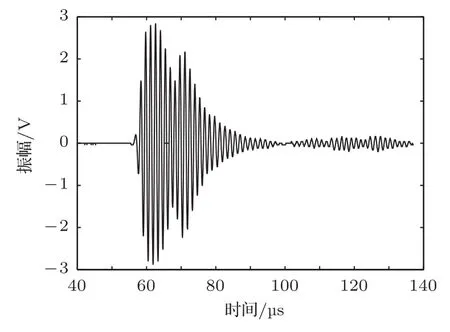
图13　铝板后探头S0波形Fig.13 S0mode waveform of second receiver in aluminum plate

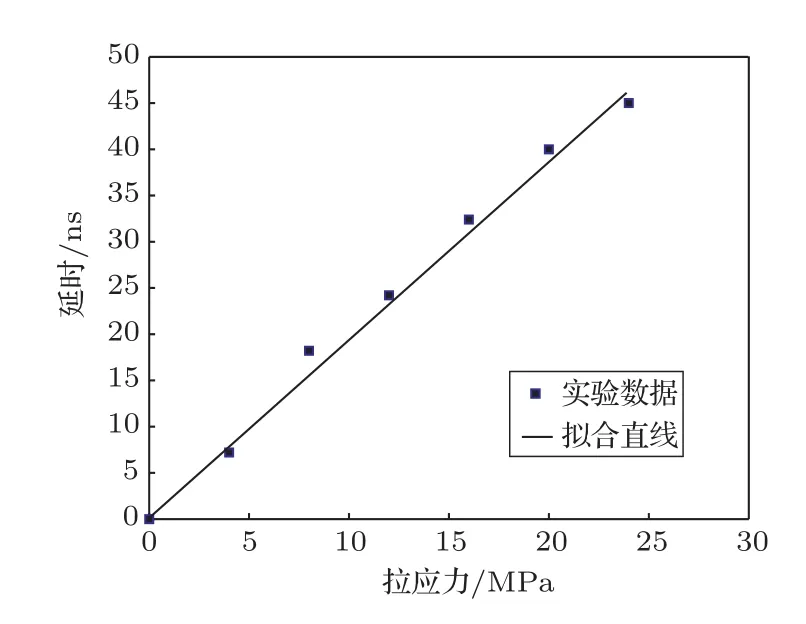
图14　铝板中S0模式的Lamb波相速度与应力关系Fig.14Relationship curve of Lamb S0mode phase velocity and stress in aluminum plate

（4）Lamb频率f=0.7 MHz，铝板厚h=1 mm，L=18.2 cm，Lamb波模式是S0模式，实测频率是0.685 MHz，测量结果及Lamb波相速度与应力关系如图12∼14所示。图12和图13的Lamb波波形有一些不一样，这主要是Lamb的频散性造成的。

由文献［3］得出

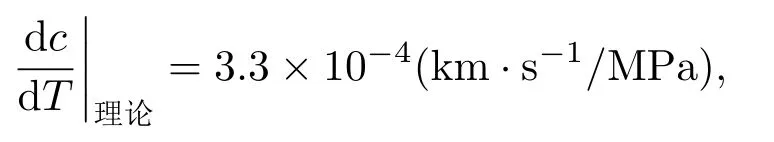
实验值

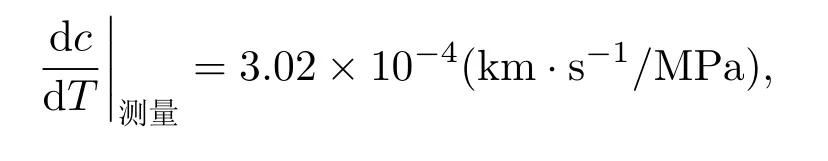
与理论值约有8.5%的相对误差。其拟合直线的线性相关系数的平方为0.9931。

由实验结果可以看出：当频厚积一定，模态一定时，Lamb波相速度对同向应力的变化率约为一常数，验证了理论结果。

5　结论

以往人们研究的波速与应力的关系都是用的非频散的波，至于有频散特性的导波与应力的关系的研究则还没有看见报道。本文是对板中Lamb波与应力关系的理论研究结果的实验验证，研究表明理论结果与实验结果至少从趋势上是一致的，这可为将Lamb波用于应力测量提供一种方法。

［1］HUGHESD S，KELLY J L.Second-order elastic deformation of solids［J］.Phys.Rev.，1953，92（5）：1145-1149.

［2］钱祖文.非线性声学［M］.北京：科学出版社，1992：324-377.

［3］王军，王寅观.金属薄板中Lamb波波速与静应力关系的理论研究［J］.声学学报，2006，31（6）：527-531. WANG Jun，WANG Yinguan.Research of relationship between Lamb wave velocity and static stress of metal plate［J］.Acta Acustica，2006，31（6）：527-531.

［4］Vinay Dayal.Leaky Lamb waves in an anisotropic plate. I：An exact solution and experiments［J］.J.Acoust.Soc. Am.，1989，85（6）：2268-2276.

Experiment on relationship between Lamb wave velocity and static stress in metal plate

WANG Jun1HAN Qingbang2
（1 Department of Mathematics and Information Engineering，Chongqing University of Education，Chongqing 400067，China）（2 College of IOT Engineering，Hohai University，Changzhou 213022，China）

In this paper，measuring device of stress gradient of Lamb wave velocity in the metal plate was designed，and principle of measurement and error were analyzed.Relationship between wave velocity and stress of the Lamb wave was studied experimentally.The results show that the velocity of Lamb wave keeps a good linear relationship with stress，and experimental value of rate of change of the relationship is in agreement with the theoretical prediction.It can provide experimental basis for Lamb wave stress measurement.

Orthogonal static stresses，Lamb wave，Dispersion equation

O422.7

A

1000-310X（2015）04-0358-06

10.11684/j.issn.1000-310X.2015.04.011

2014-10-18收稿；2015-03-09定稿

∗国家自然科学基金项目（11274091），重庆第二师范学院校级项目

王军（1964-），男，重庆人，博士，教授，研究方向：非线性声学。†

E-mail：tjcwangjun2009@163.com