水平不变浅海环境随机扰动对声传播的影响∗

王文博　黄　勇　李淑秋

（1中国科学院声学研究所　北京　100190）

（2中国科学院大学　北京　100049）

水平不变浅海环境随机扰动对声传播的影响∗

王文博1,2†黄勇1李淑秋1

（1中国科学院声学研究所北京100190）

（2中国科学院大学北京100049）

本文主要讨论浅海水平不变波导中的低频声传播问题，为环境适配声纳设计奠定基础。通过仿真分析了海水及海底环境参数对传播损失的影响，根据仿真及实验结果，建立了声速剖面随机扰动及海面、海底起伏条件下的声强分布概率模型，并利用模型中的形状参数α和尺度参数β，提出了局部蒙特卡洛模拟加曲线拟合的声场敏感性分析方法。仿真及实验结果表明声场传播损失服从伽马分布，良好水文条件下10 km距离的声场能量起伏也达到10 dB，随着距离增加，声场敏感性增加。本文所提出方法通过对近场声场的测量和统计实现对远场声场敏感性的预报，与全声场蒙特卡洛模拟相比计算量减小一个数量级。

传播损失，声场敏感性，形状参数，尺度参数

1　引言

浅海环境变化特性对声传播的影响直接关系到声纳检测性能好坏，因而成为联系海洋声学与声纳信号处理的热点研究领域。浅海声传播的一个显著特征是阳光、大气等因素引起的热对流使海水温度在较短时间内发生较大变化，从而浅海声速剖面随机扰动相当剧烈。而声速剖面的很小变化就足以影响海洋中声传播特性［1］，因此声速剖面时空扰动往往是造成浅海声场能量波动和相位起伏的最重要因素。浅海声传播的另一个显著特征是声波频繁作用于海面和海底。粗糙的海面和海底增加了声波与上、下边界的作用次数，从而引起更多的散射衰减并使更多的能量渗透到沉积层中［2］。通常海水的声阻抗远大于空气，因此海面可以看作压力释放界面，反射系数为-1，即空气吸收带来的能量衰减忽略不计，一般只需考虑海面波浪起伏所引起的声能量散射衰减。海底分层结构和沉积层中的横波使得海底的情况比海面复杂得多。声波能够穿透海底沉积层的厚度与声波波长处于同一量级，通常为一到两个波长。因此声波频率越高海底分层结构的影响越不明显，对于高声速海底和小掠角入射尤其如此。对于频率大于1 kHz的声波，声场建模仿真仅需要知道沉积层几米之内的海底组成细节，同时海底反射系数由地形决定［3］。对于沉积层中的横波，KRAKEN模型和SCOOTER模型的计算结果表明：对于频率大于300 Hz的声波，当横波速度小于500 m/s时，渗透进入沉积层的声能量可以忽略。声速随机扰动和海深不确定对声场的影响比引入横波的影响大得多［4］。实验SW06表明：对于中心频率1.2 kHz、带宽200 Hz、脉宽0.5 s的线性调频声信号，沉积层厚度和基底底质特性对声传播的影响微乎其微［5］。

在上述研究工作基础上，本文讨论了水平不变波导中300 Hz声信号的传播问题。首先，针对负弱梯度浅海模型，仿真分析了各环境参数对声传播的影响。然后，利用仿真和实验结果，建立了声速剖面随机扰动及海面、海底起伏条件下的声强分布概率模型。最后，使用概率模型中的形状参数和尺度参数，提出了局部蒙特卡洛模拟加曲线拟合的声场敏感性分析方法。

2　海洋环境对声传播的影响

海水中单频点声源激发的声场可表示为一系列简正波的叠加，对于二维模型，声压为

其中，µn=kn+iδn，kn为水平波数，δn为简正波衰减系数，ϕn（·）为第n号模态函数，H0（·）为零阶汉克函数。海洋环境对声传播的影响可用δn表征：

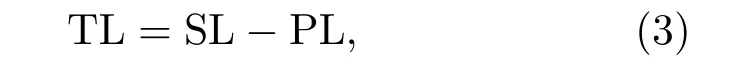
其中，SL为声源级，PL为接收信号的声强级，PL=20lg|p|。取声源为单位强度，则传播损失TL=SL-PL=-20lg|p|。

2.1传播损失随距离变化的仿真结果

仿真采用环境模型为弱负梯度类型浅海，这也是实验的海洋环境。海底分层结构为粘土-粘沙沉积层覆盖在岩石基底上，如图1所示。实验场景为100 km拉距实验，声源深度30 m，采用阵元间距1 m的90元垂直阵接收信号，信号频率300 Hz。本文采用2000次蒙特卡洛随机抽样进行模拟仿真。

通过蒙特卡洛模拟得到环境参数对声传播损失的影响，图2为20 m、50 m和90 m三个接收深度的传播损失随距离变化情况。随着距离增加，传播损失不确定性增加。海水声速剖面扰动、海面波浪起伏、海底地形起伏对传播损失影响很大。海水深度的变化可显著改变声场结构，造成声场能量的空间周期起伏。除沉积层厚度外，其他沉积层参数对传播损失影响较大，沉积层厚度只对近距离且靠近海底的声场能量分布有较大影响，如接收深度90 m且距离小于2 km时传播损失标准差大于3 dB。岩石层参数对传播损失的影响可以忽略，所以对于远距离声传播，海洋环境模型可近似为海水加半无限液态沉积层二层结构。同时在观测时间内，标称海深和沉积层参数的时变特征不明显，所以环境变化主要体现为海水声速剖面扰动、海面波浪起伏、海底地形起伏。

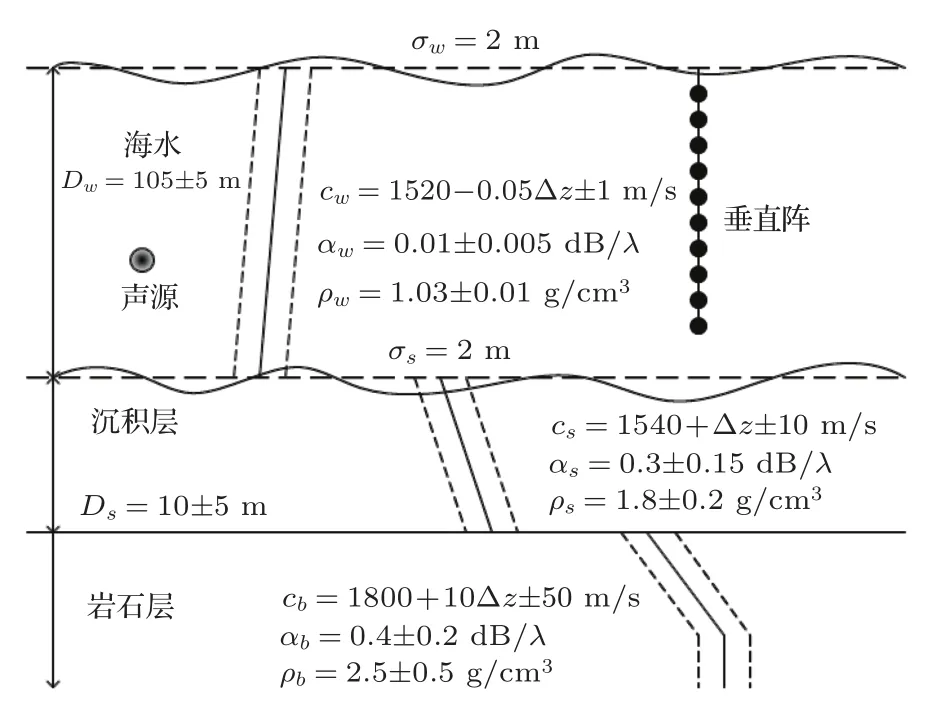
图1　仿真环境模型：负弱梯度浅海（c为声速，α为吸收系数，ρ为密度）Fig.1 Environment model of simulation，weak negative gradient sound speed profile in shallow water（c is sound speed，α is absorption coefficient，ρ is density）

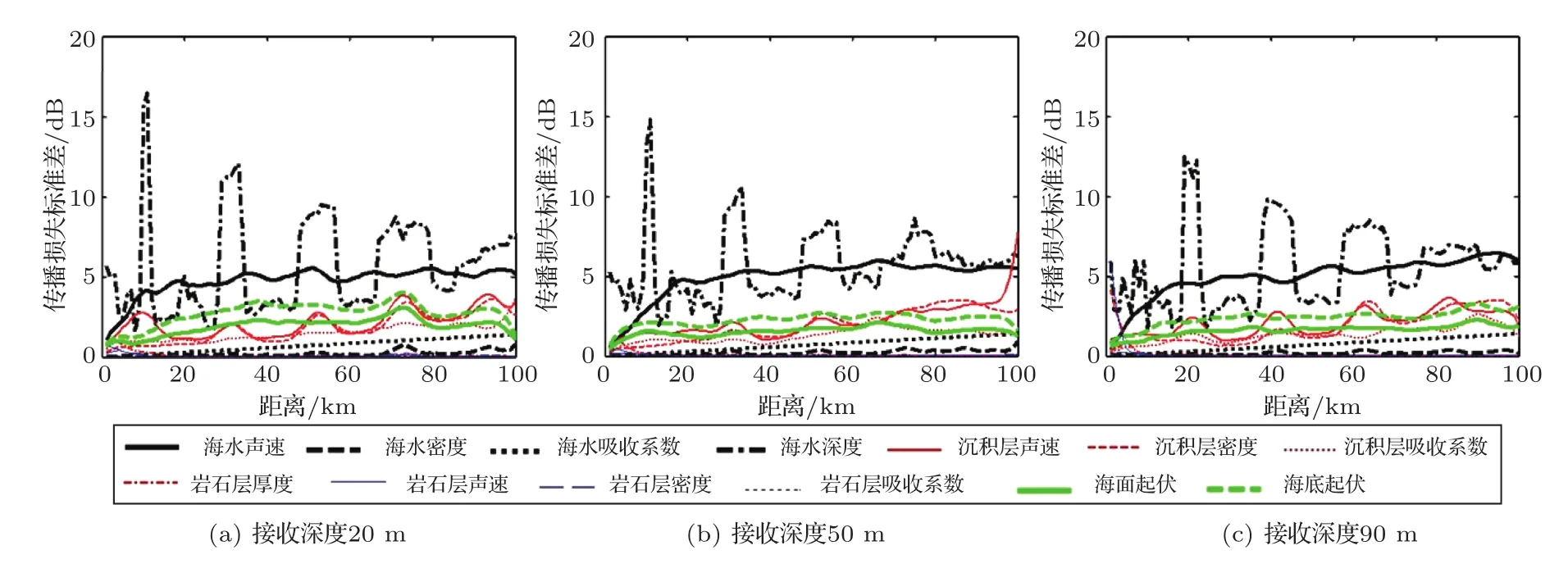
图2　海洋环境参数对声传播损失的影响Fig.2 Impact of ocean environment parameters on the acoustic transmission loss

2.210 km定点实验及声传播损失分布

10 km定点实验及模型仿真考察1 m/s声速剖面随机扰动、2 m海面起伏和2 m海底起伏等条件下的声传播损失分布规律。图3为20 m、50 m和90 m三个接收深度传播损失分布的仿真和实验结果。图3表明传播损失分布接近单峰伽马分布，仿真与实验结果基本吻合。即便对于良好海况和良好水文条件，90%置信水平的声场能量起伏也有10 dB左右。比较模型数据拟合曲线和实验数据拟合曲线，实验结果方差更小，原因是实际的海底空间起伏不随时间变化，但由于它是未知的，仿真中每次海底空间起伏的实现都不同，造成了更分散的传播损失分布。

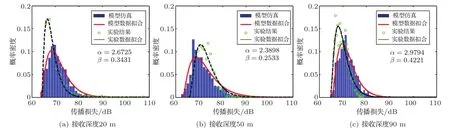
图3　声传播损失的分布规律的仿真及实验结果Fig.3 Distribution of acoustic transmission loss in simulation and experiment

3　声强分布的形状参数与尺度参数

由10 km定点实验结果可知，声场中各点传播损失服从伽马分布，声强分布是传播损失分布的对称平移：

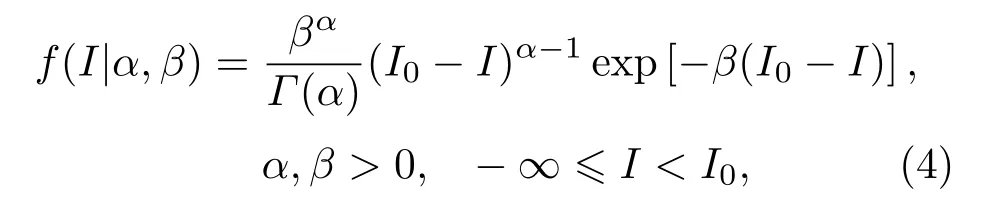
其中，声强I、I0、形状参数α、尺度参数β均与声源深度zs、接收位置（ri，zj）、环境参数Ψ有关。环境时变特性导致声场不确定，即不同时刻声强测量值的集合服从（4）式分布。由（4）式不难计算声强的期望和方差分别为

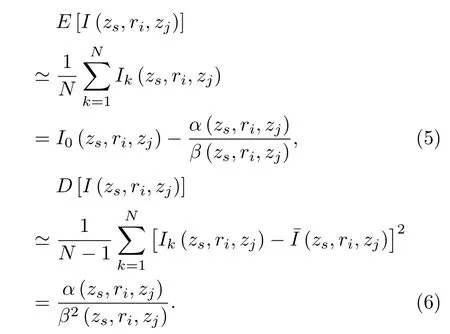
由（5）式 和（6）式 可 计 算α（zs，ri，zj）和β（zs，ri，zj）。仿真结果表明固定声源深度zs和接收深度zj，α与接收距离ri呈线性关系，β与接收距离ri呈弱指数关系：

图4为声源深度30 m、接收深度20 m、50 m和90 m时α和β随接收距离的变化情况，验证了（7）式和（8）式的正确性。

4　声场敏感性快速预报

声场敏感性描述了水声信道对环境变化的响应程度，是度量声场由环境模型过渡到传播模型时变化特征的量，定义为［8］

其中，σ（I）为声强标准差，⟨I⟩为声强均值。

对于给定的环境模型如图1，可通过全声场蒙特卡洛模拟获得声场敏感性，计算量达到O（MNKL），M、N、K、L分别表示水平采样数、深度采样数、模态数、模拟（或测量）次数。

图4　形状参数和尺度参数随接收距离变化，声源深度30 m，接收深度20 m、50 m、90 mFig.4 Shape parameter and scale parameter versus range，the source depth is 30 m，receiver depths are 20 m，50 m and 90 m，respectively

通过对近距离（如1～5 km）声场的测量（或模拟），并按（7）式和（8）式进行曲线拟合，得到全声场的形状参数和尺度参数，从而实现对远场声场敏感性预报。声场敏感性计算式为

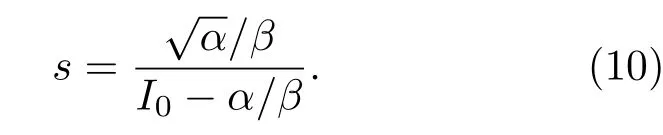
图5为分别用两种方法产生的声场敏感性图像，结果一致。同一深度，随着距离增加，声场敏感性增加；同一距离，声源深度处（30 m）的声场敏感性最大。对于远距离声场敏感性预报，局部蒙特卡洛模拟加曲线拟合方法的计算量约为O（NKL），比全声场蒙特卡洛模拟方法的计算量减小了一个数量级。

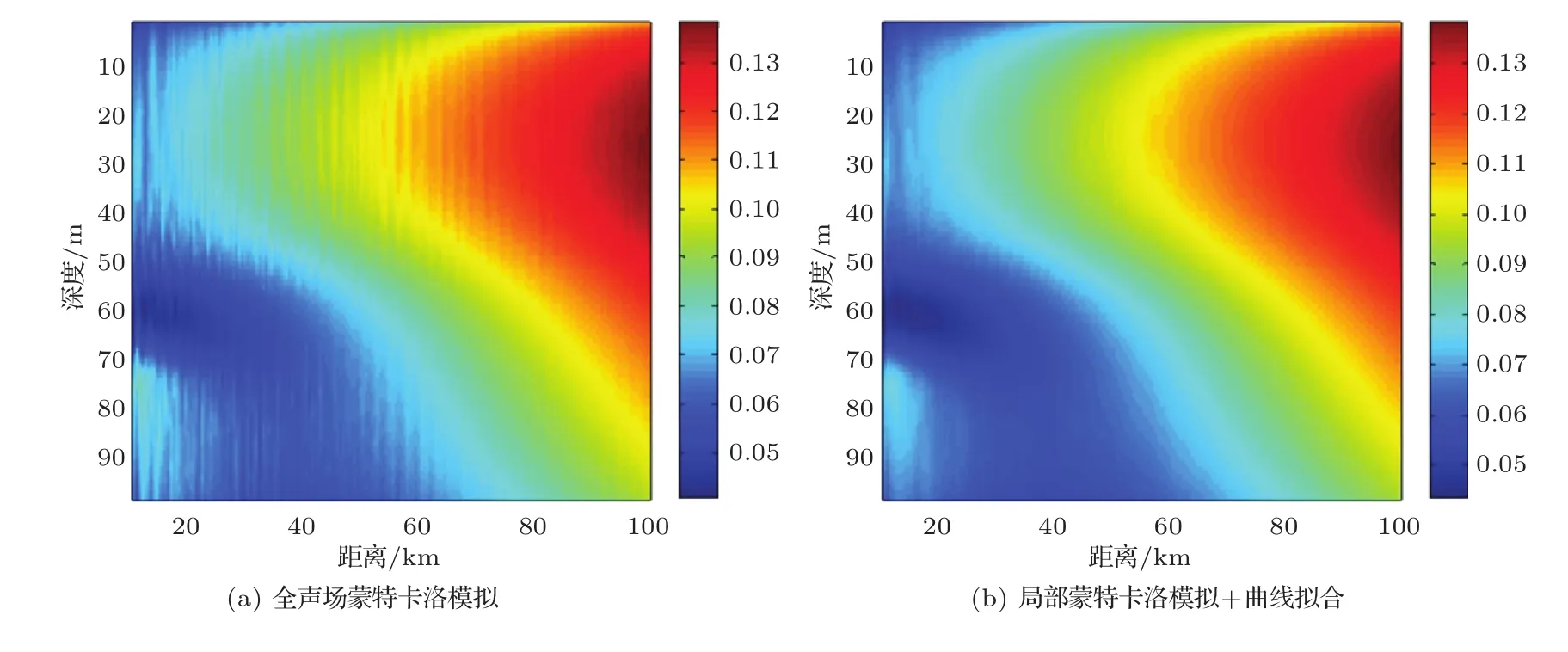
图5　声场敏感性图像，声源深度30 mFig.5 Sound field sensitivity，the source depth is 30 m

5　讨论和结论

本文研究了浅海水平不变波导由环境模型传递到传播模型时声场的变化规律，通过对仿真及实验结果的分析，得到了若干定性和定量结论：频率大于300 Hz的声传播，海面及海底起伏的影响十分显著。同时存在声速剖面随机扰动和海面、海底起伏的情况下，声场传播损失分布接近单峰伽马分布。良好水文条件下10 km距离的声场能量起伏也达到10 dB，随着距离增加，声场敏感性增加，同一距离处，声源深度的声场敏感性最大。

本文还利用声强分布的形状参数α和尺度参数β，提出了局部蒙特卡洛模拟加曲线拟合的声场敏感性方法。仿真中通过模拟距离5 km内的声场并进行统计计算，成功预报了100 km内的声场敏感性，计算速度有很大提高。

传统上认为环境变化会造成声纳模型失配，降低探测、定位性能。事实上，如果本文研究的声强分布（或其他声学量）具有普适性，则分布参数（或其他统计特征）将与声源位置及环境参数有关，这就为匹配定位或声学反演提供了可能性。这些还有待更进一步的理论和实验研究。

［1］BREKHOVSKIKH L M，LYSANOV Yu P.Fundamentals of ocean acoustics［M］.New York：Springer-Verlag，2002.

［2］ROUSEFF D，EWART T E.Effect of random sea surface and bottom roughness on propagation in shallow water［J］. J.Acoust.Soc.Am.，1995，98（6）：3397-3404.

［3］李启虎，荣新光.海洋水声环境和声纳设计手册［M］.北京：海潮出版社，2011.

［4］STOJANOVIC M.Recent advances in high-speed underwater acoustic communications［J］.IEEE J.Oceanic Eng.，1996，123（4）：125-136.

［5］PECKNOLD S P，MASUI K W，HINES P C.Transmission loss measurements and geoacoustic sensitivity modeling at 1.2 kHz［J］.J.Acoust.Soc.Am.，2008，124（3）：110-115.

［6］FRISK G V.Ocean and seabed acoustics：a theory of wave propagation［M］.Indiana：Prentice Hall PRT，1994.

［7］DUNCAN A.Underwater acoustic propagation modeling software—AcTUP V2.2L［DB/OL］.Perth：Curtin University，［2014-05-27］.http：//www.cmst.curtin.edu.au/products/actoolbox/index.html.

［8］DOSSO S E，MORLEY M G，GILES P M，et al. Spatial field shifts in ocean acoustic environmental sensitivity analysis［J］.J.Acoust.Soc.Am.，2007，122（5）：2560-2570.

Effects of random environmental disturbance on sound propagation in range-independent waveguide in shallow water∗

WANG Wenbo1，2†HUANG Yong1LI Shuqiu1

（1 Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China）

（2 University of Chinese Academy of Sciences，Beijing 100049，China）

Low-frequency sound propagation through range-independent waveguide in shallow water,which lays the foundation for environment adapted sonar design,was discussed in the present work.Impacts of environmental parameters（i.e.seawater and seabed quality）on transmission loss were analyzed through simulation.The probability model of intensity distribution in conditions of random sound-speed perturbations, rough sea surface and bottom was established according to simulation and experimental results.Using shape parameter α and scale parameter β in model,a sensitivity analysis method by local Monte Carlo simulation plus curve fitting was proposed.Experimental measurements and simulation results suggest that transmission loss obeys the gamma distribution.Energy fluctuation reaches the level of 10 dB at the distance of 10 kilometer for favorable hydrological conditions,and the acoustic field sensitivity increases as the distance increases. The proposed method forecasts far-field sensitivity by near-field measurements and statistics,its calculation complexity is an order of magnitude less than that of global Monte Carlo simulation.

Transmission loss,Acoustic environmental sensitivity,Shape parameter,Scale parameter

O427.9

A

1000-310X（2015）01-0090-05

10.11684/j.issn.1000-310X.2015.01.014

2013-09-12收稿；2014-05-27定稿

∗国家自然科学基金项目（10904160）

王文博（1986-），男，内蒙古赤峰人，博士研究生，研究方向：信号与信息处理。

E-mail：jaynesacademic@163.com