内部激励源二自由度结构扬声器振动特性分析∗
刘云峰 沈 勇† 夏 洁 章志亮
(南京大学声学研究所 近代声学教育部重点实验室 南京 210093)
⋄研究报告⋄
内部激励源二自由度结构扬声器振动特性分析∗
刘云峰沈勇†夏洁章志亮
(南京大学声学研究所近代声学教育部重点实验室南京210093)
有别于多数基于简单振子结构的扬声器,针对一类内部激励源二自由度(IE2DOF)结构的扬声器,用类比线路图法建立集总参数模型,计算分析了这种结构的频率响应,同时计算了其固有共振频率和固有反共振频率。使用叠加法分析内部激励源对频响的影响。最后实际测量和理论计算吻合,进一步支持了理论模型,揭示了IE2DOF结构扬声器的振动特性。
二自由度,内部激励源,反共振,扬声器
1 引言
上个世纪70年代以来,线性集总参数模型被广泛用于动圈式扬声器的分析[1-3]。其中振动部件的质量和悬置部件的力顺构成了一个基本的简单振子力学模型。其他类型扬声器,包括电磁式、静电式、压电式等,也大多基于相同力学结构。它是一个由外力驱动的单自由度(Single-degree-offreedom,SDOF)结构。然而在一类扬声器中,存在一种内部激励源二自由度(Internal-excitation 2-degree-of-freedom,IE2DOF)结构,会产生额外的共振与反共振现象。在如图1(a)所示的平板扬声器中,平板与激励器,由一对相互作用力驱动,都参与了系统的振动。但由于其多工作于分布式振动频带,这种结构未得到充分分析[4-5]。在如图1(b)所示的结构中,磁路部分通过弹性介质固定,磁路在音圈的反作用力下会在特定频率产生额外的共振。当扬声器安装于非刚性箱体时,这种结构将会产生有害的箱体结构振动问题。另外,弯曲振动模式的压电扬声器也拥有类似结构。这几种情况都拥有相同的IE2DOF结构,图1(c)是IE2DOF结构的力学示意图。此外,沙家正、张志良等在对扬声器中频谷点以及分谐波失真的研究中,也发现了类似的共振与反共振现象,虽激励方式不一样,但它们也拥有类似的二自由度结构[6-7]。针对此类扬声器,如何建立模型进行准确分析成为本文的研究重心。
本文对IE2DOF结构扬声器的振动特性进行了分析。用类比线路图法,对其建立集总参数模型,计算其位移响应。结果显示这种结构会产生额外的共振与反共振现象。本文给出了共振频率与反共振频率的解。用叠加法分析了不同激励模式对系统输出的影响。最后进行实际测量,测量结果很好地支持了之前的计算。本文对IE2DOF结构的分析,有助于在平板扬声器、压电弯曲振动扬声器、扬声器非刚性固定等应用领域,实现更优化的设计。
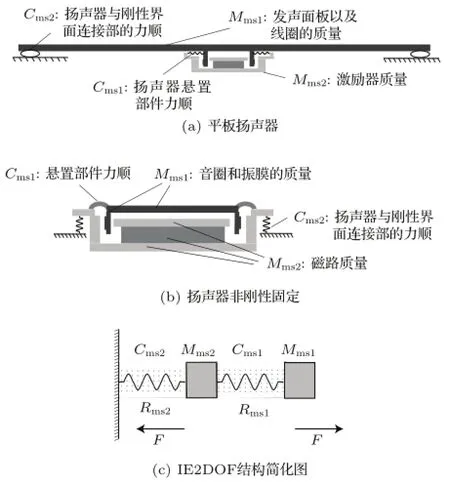
图1 扬声器中的IE2DOF结构Fig.1 IE2DOF structure in loudspeakers
2 理论模型与分析
2.1类比线路模型分析
分析图1(b)所示扬声器的力学性质,可用导纳型类比电路图法建立图1(c)中IE2DOF结构扬声器类比线路模型(如分析图1(a),需要将图1(c)中两个质量符号调换)。在导纳型类比中,力学量质量、力顺、阻尼分别等效为电路中的电容、电感和电导,速度对应于电压,力对应于电流。这样可以得到其类比线路模型,如图2所示。其中
Mms1为振膜以及音圈的质量;
Mms2为激励源质量;
Cms1为振膜与磁路间悬置部件的力顺;
Cms2为扬声器与刚性界面之间弹性连接处的力顺;
rms1=1/Rms1,为音圈与磁路相对运动产生的机械阻尼;
rms2=1/Rms2,为扬声器与刚性界连接处的内部机械阻尼。
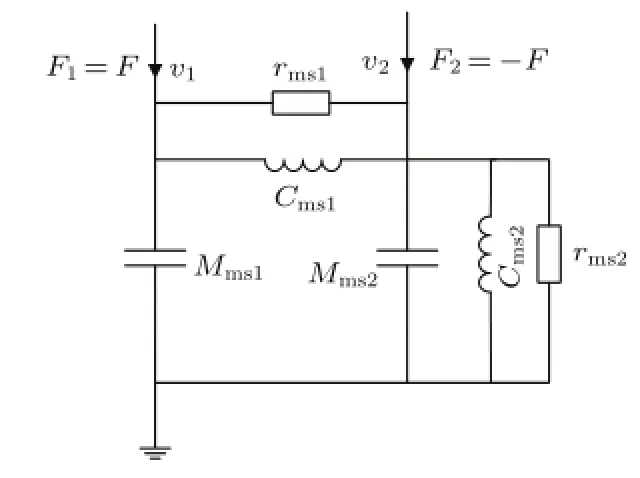
图2 导纳型IE2DOF结构的类比线路模型Fig.2 Mobility-type analogous circuit model of IE2DOF structure

利用上述方程组式(1)便可以求出两个振子Mms1、Mms2在不同频率激励下的速度v1、v2。
为简化起见可以首先分析无阻尼的情况。忽略阻尼rms1、rms2,可以求得速度v1和v2的表达式,同时根据速度与位移的关系ξ=∫vdt,可进一步得到质量体Mms1的位移ξ1和质量体Mms2的位移ξ2的表达式:

由(2)式可得,对于ξ1,分母部分在ω=ω2和ω=ω3时为零,ξ1趋近于无穷大,表明ω=ω2和ω=ω3都是ξ1的共振频率。而在ω=ω1处,ξ1分子部分为零,表明ω=ω1是零位移点,即反共振频率。对ξ1绘制如图3(a)所示曲线,可以发现ξ1具有“共振-反共振-共振”的性质。
由(3)式可得,对于ξ2,分母部分在ω=ω2和ω=ω3时为零,ξ2同样趋近于无穷大,表明ω=ω2和ω=ω3同样是ξ2的共振频率。而与ξ1不同的是不会出现零位移点(或者说在频率为零处出现了零位移点,这也是与简单振子模型不同的)。对ξ2绘制如图3(b)所示曲线,可以发现ξ2具有两个共振峰的性质。
类似于简单谐振子中的情况[8-9],可将ω1视为系统的固有反共振频率,ω2、ω3视为系统的固有共振频率。当Mms2→ +∞或者Cms2=0时,IE2DOF模型变成了一个简单振子模型,其中
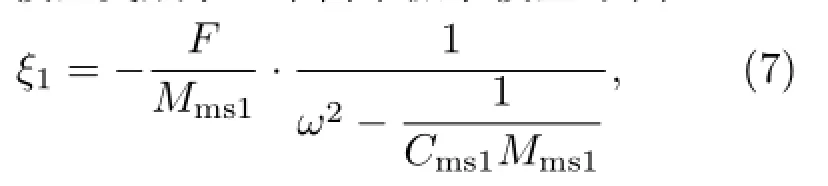
正是典型的简单振子模型位移响应。
在实际情况中,阻尼的存在会对上述结果产生影响。在简单振子模型中,简谐振子的阻尼对共振峰大小和位置产生了影响[8-9]。对上面位移响应的计算考虑了阻尼之后,其曲线如图3中虚线曲线所示。对比无阻尼情况,共振峰的峰值与反共振峰的下潜幅度有所降低,对应频率也出现偏移,这与简单振子模型一致。此外,由于变量较多,不同的质量、力顺组合带入位移公式也会得到不同的频响形状,读者可以尝试更多组合来看看频响的具体形状,最终会发现都会呈现上文总结的几种特征。
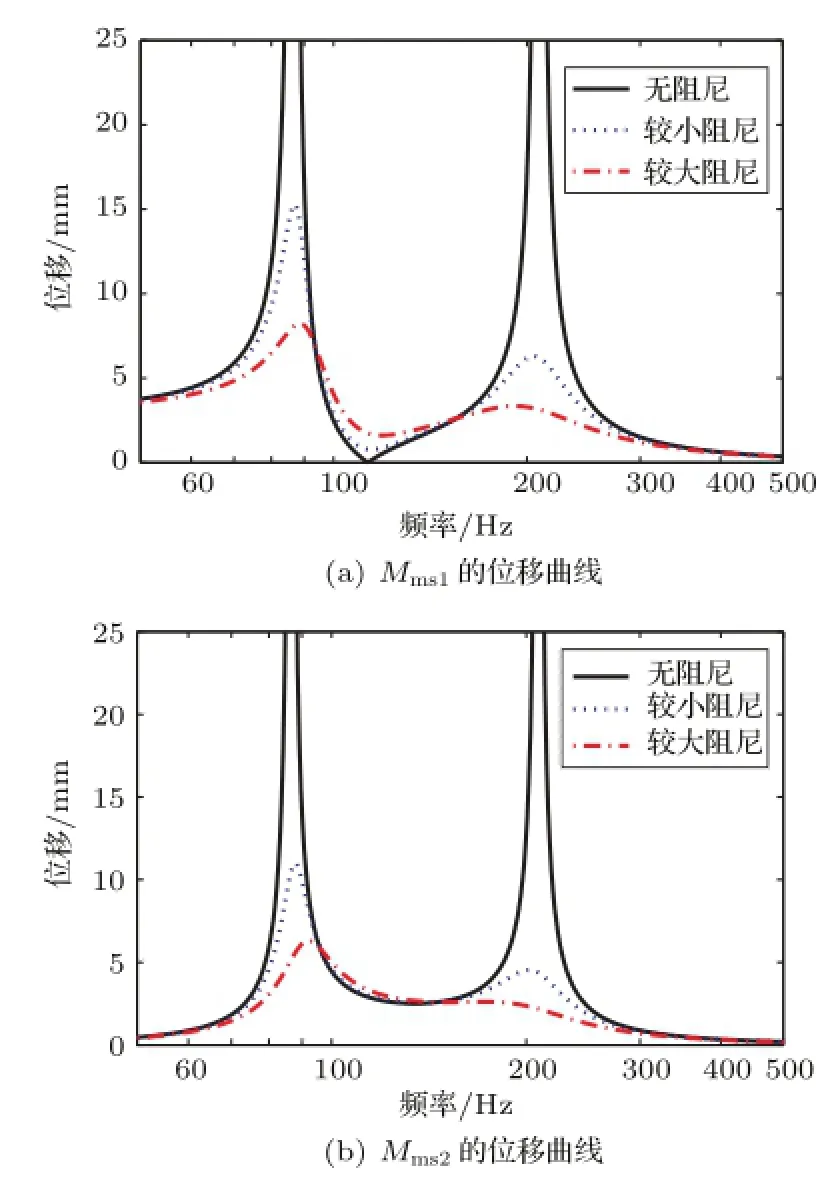
图3 Mms1与Mms2的位移曲线Fig.3 Displacement curve of Mms1and Mms2
2.2内部激励源分析
IE2DOF结构一个重要的特点是激励源由内部一对相互作用力组成,所以称之为内部激励源,这是除了二自由度结构外,不同于简单振子模型的另一处不同点。为了研究这种内部激励方式对系统输出响应的影响,叠加原理在此处被使用。
IE2DOF结构可以看做一个二激励源系统,两个驱动力大小相等,方向相反。由于电学、力学的类比性和电路中的叠加原理,它可以视为两个单激励源系统的线性叠加,后者等效线路模型如图4所示。
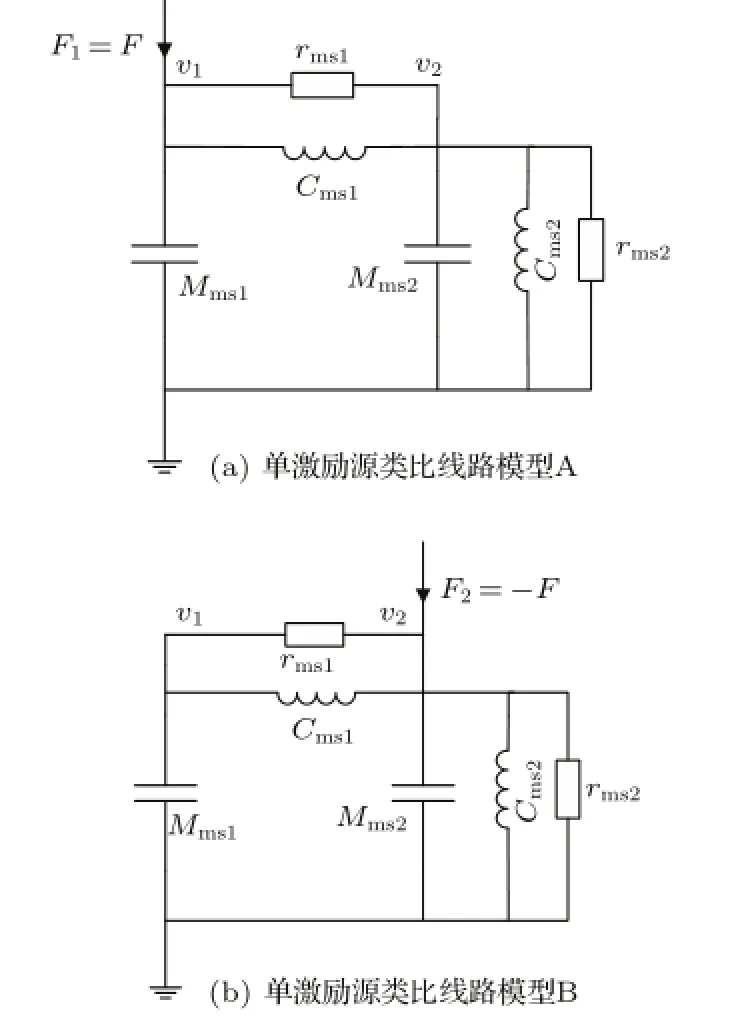
图4 单激励源类比线路模型A和模型BFig.4 Single-excitation model A and model B
当F1=F,F2=0时,系统的类比线路模型如图4(a)所示,其位移响应为

而当F1=0,F2=-F时,系统的类比线路模型如图4(b)所示,其位移响应为
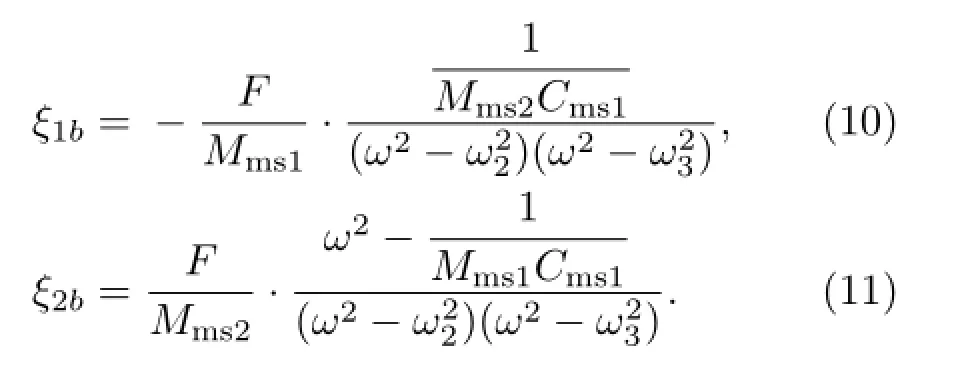
其中ω2和ω3的表达式在式(5)、式(6)中已经给出。
当以上两种情况线性叠加时,IE2DOF系统的响应便可以得到。对于质量体Mms1,位移响应为ξ1a+ξ1b,对于质量体Mms2,位移响应为ξ2a+ξ2b。它们正好与式(2)和式(3)相等。
比较三种不同激励模式下的结果,即式(2)、式(3)、式(8)、式(9)、式(10)、式(11)可以发现:在所有三种模式下,分母部分相同,即共振特性相同,共振频率在式(5)和(6)中已经给出。但是比较分子部分,发现它们的反共振性质不同。当激励仅仅施加在Mms1上时,Mms1在角频率[(Cms1+Cms2)/(Mms2Cms1Cms2)]1/2处产生反共振。当激励仅仅施加在Mms2上时,Mms2在角频率[1/(Mms1Cms1)]1/2处产生反共振。当系统由内部两个相互作用力激励时,由于叠加效应,Mms1和Mms2应当都有反共振性质。但是叠加后,Mms2的反共振频率移到了零点,所以在图3(b)中,看起来Mms2似乎没有出现反共振(实际出现在了频率为零处)。
3 实验验证
为验证理论模型的可靠性,对一款IE2DOF结构的动圈扬声器(基于图1(b)结构)进行实际测量的对比。实验中实际使用了一款11 mm×15 mm的微型扬声器,将其通过泡棉与刚性界面连接组成一个简单的IE2DOF结构。实验示意图如图5所示。
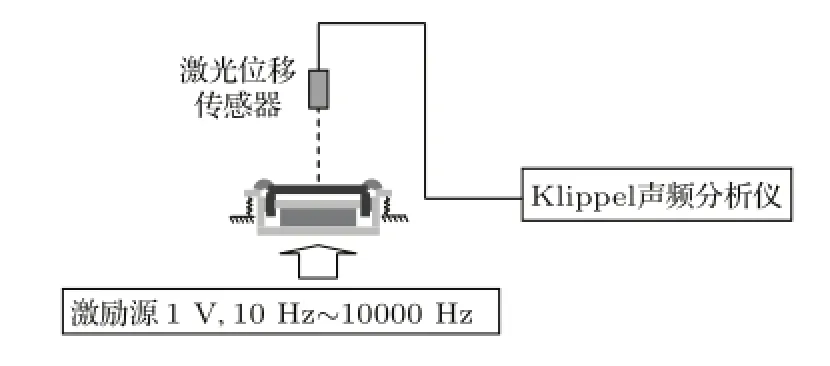
图5 测量实验示意图Fig.5 A schematic diagram of the measuring experiment
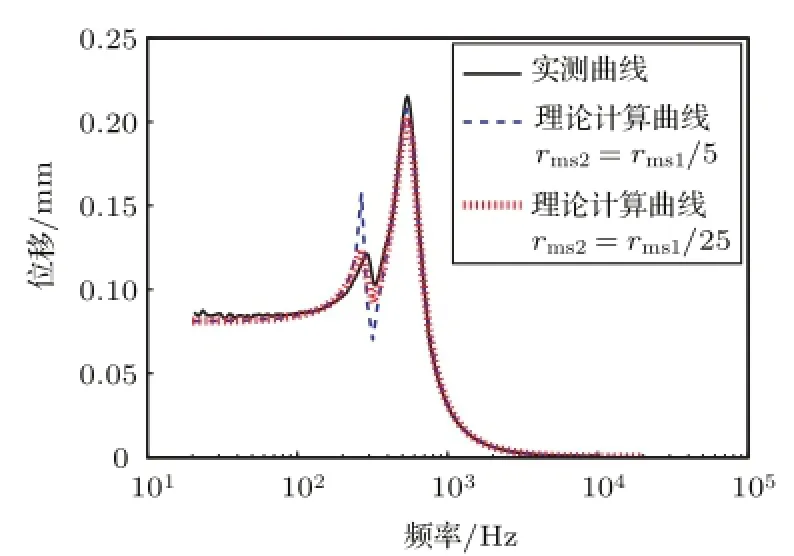
图7 IE2DOF结构扬声器的位移频响的实测与计算比较Fig.7 Comparison between measurement and calculation of an IE2DOF structure loudspeaker’s displacement response
由于需要考虑电学负载和声学负载,在图2所示线路图的基础上,将线圈电阻电感和声学负载耦合进去,可以得到扬声器完整的等效线路模型,如图6所示。对电路模型分析可以计算得到扬声器振膜的位移曲线。而计算所需大部分参数,除阻尼rms2无法直接测得外,都可以直接或间接测得。(将Mms2人为固定后,IE2DOF结构即可转化为简单振子模型,即可用附加质量法等一般TS参数测量法测得Cms1、rms1和Mms1,Mms2和Cms2可以另外单独测得。本次计算参数:Re=7.41 Ω,Le=0.05 mH,BL=0.986 N/A,Mms1=0.146 g,Cms1=0.619 mm/N,rms1=27.05 s/kg,Mms2= 2.34 g,Cms2=0.124 mm/N)那么可以计算出不同阻尼rms2下的一组曲线,与实测曲线比较。本文选取了rms2=rms1/25和rms2=rms1/5的两组曲线,如图7所示。
对比实验数据和理论计算,发现两种阻尼情况下,位移频响曲线上峰与谷与理论计算趋势一致,当rms2=rms1/25时,两者吻合得很好。两者基本在相同的频率上都出现了共振与反共振现象,并且幅度基本一致。当然仔细对比,实测与计算所得的共振峰的位置还是由一定差异的,一方面计算所用参数的测量存在一定误差(如小信号参数与实际较大振幅下的实际参数存在差异),另一方面与模型本身的精确度有关(此处声负载做了简化处理,忽略了声阻)。但总体还是证明了之前所建立的IE2DOF结构理论模型是可靠的。
4 结论
内部激励源二自由度(IE2DOF)结构的扬声器不能简单当作单自由度的简单振子模型进行处理。本文通过类比线路图法,对IE2DOF结构建立类比线路模型,分析了系统的稳态频域响应。结果表明这种结构中,出现了二次共振现象以及反共振现象。文章给出了共振频率与反共振频率的解。同时利用叠加原理,研究了内部激励源的影响。为验证理论的可靠性,进行了验证测量。实验结果和理论模型拥有很好的吻合度,支持了之前的理论分析。
[1]THIELE A N.Loudspeakers in vented boxes.1[J].Journal of the Audio Engineering Society,1971,19(5):382-392.
[2]THIELE A N.Loudspeakers in vented boxes.2[J].Journal of the Audio Engineering Society,1971,19(6):471-483.
[3]SMALLRH.Direct-radiatorloudspeakersystemanalysis[J].Journal of the Audio Engineering Society,1972,20(5):383-395.
[4]BAI M S R,HUANG T L.Development of panel loudspeaker system:Design,evaluation and enhancement[J]. Journal of the Acoustical Society of America,2001,109(6):2751-2761.
[5]BAI M R,LIU B.Determination of optimal exciter deployment for panel speakers using the genetic algorithm[J].Journal of Sound and Vibration,2004,269(3):727-743.
[6]沙家正.扬声器中频谷点的研究[J].电声技术,1986,(3):1-4.
[7]张志良,刘世清,李小菊.有内共振时的扬声器分谐波和混沌[J].声学学报,2012,37(4):386-392. ZHANG Zhiliang,LIU Shiqing,LI Xiaoju.Subharmonics and chaos in loudspeakers with internal resonance[J]. Acta Acustica,2012,37(4):386-392.
[8]MORSE P M,INGARD K U.Theoretical Acoustics[M]. Princeton:Princeton University Press,1986.
[9]杜功焕,朱哲民,龚秀芬.声学基础[M].南京:南京大学出版社,2001.
Dynamic behavior of a kind of internal-excitation 2-degree-of-freedom structure loudspeaker
LIU YunfengSHEN YongXIA JieZHANG Zhiliang
(Key Laboratory of Modern Acoustics,MOE,and Institute of Acoustics,Nanjing University,Nanjing 210093,China)
For a kind of internal-excitation 2-degree-of-freedom(IE2DOF)structure loudspeaker,which is different from the most common simple oscillator structure,analogous circuit method is used to build a lumped parameter model.Its frequency response is calculated and analyzed.The natural resonant and anti-resonant frequencies are also given.Superposition method is used to analyze the influence of the internal excitation pattern.Measuring result supports the calculation very well.This research reveals the dynamic behavior of such kind of IE2DOF structure loudspeakers.
2-degree-of-freedom,Internal excitation,Anti-resonance,Loudspeaker
O42
A
1000-310X(2015)03-0260-06
10.11684/j.issn.1000-310X.2015.03.012
2014-08-19收稿;2015-04-02定稿
∗有限长近似线声源声学特性研究(11274172)
刘云峰(1989-),男,江苏泰州人,硕士研究生,研究方向:电声学。†
E-mail:yshen@nju.edu.cn

