基于流速面积法的明渠流量测量不确定度评定

赵伟国， 王成李， 朱 炜， 戴连超

（1.中国计量学院，浙江 杭州 310018； 2.杭州市质量技术监督检测院，浙江 杭州 310019）

基于流速面积法的明渠流量测量不确定度评定

赵伟国1， 王成李1， 朱 炜2， 戴连超1

（1.中国计量学院，浙江 杭州 310018； 2.杭州市质量技术监督检测院，浙江 杭州 310019）

针对ISO 748进行明渠流量测量不确定度评定，需在测量断面上设置充足的垂线数和测点，且没有考虑底层、表层和两边壁盲区流速插补引入的不确定度问题，提出了一种新型明渠流量测量不确定度评定方法。通过Fluent数值模拟，得出明渠断面垂线流速分布模型和横向平均流速分布模型。在实验测量中，根据两者流速模型分别计算出断面垂线测点不足和垂线数不足引入的不确定度，对明渠流量测量的不确定度进行了评定。结果表明，该方法提高了明渠流量测量不确定度评定的准确性。

计量学；流量测量；明渠；数值模拟；不确定度；流速分布模型

1　引 言

目前，采用流速面积法的明渠流量测量不确定度评定是依据经验公式或理论研究进行的。Pelletier［1］提出了明渠流量测量不确定度的影响因素，但没有独立考虑底层、表层及边壁盲区流速插补影响引入的不确定度；Simpson［2］提出了一个声学多普勒测速仪的流量测量不确定度评定的相对标准预测模型，也没有考虑表层及底层盲区流速插补引起的不确定度分量。Le Coz J［3］对表层、底层流速插补采用常数法，不利于提高流量测量不确定度的评定准确性。明渠断面可分为壁面区域、半深度区域和自由水面区［4］，本文基于明渠流动的紊流特征及流速分布特点，研究明渠断面3个区域流速分布，将流速分布模型引入不确定度评定方法中，实现了明渠流量测量的不确定度评定。

2　数学模型

采用流速面积法的明渠流量测量不确定度u（Q）为［5］

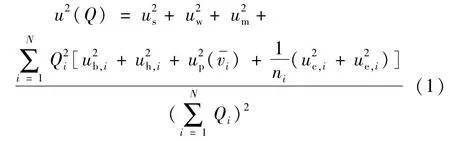
式中：Qi为第i个断面的流量；us为测量仪器引入的不确定度；uw为明渠断面两边壁盲区流速插补引入的不确定度；um为垂线数不足引入的不确定度；ub，i和uh，i分别为第i个断面明渠宽度和水深测量随机误差引入的不确定度；up（）为平均流速在第i个断面上测点不足引入的不确定度；ni为垂线i上测点数；uc，i、ue，i分别为测速仪在第i个断面流速重复性和测速历时引入的不确定度。

垂线测点不足引入的不确定度通过垂线流速分布模型计算得到，垂线数不足和边壁盲区流速插补引入的不确定度通过横向平均流速分布模型计算得到，两者模型由Fluent数值模拟结果得到。

2.1垂线流速分布模型

将明渠断面分区域进行流速分布研究，引入无量纲量y/h（y为测点距底壁的距离，h为水深）和v/ u（v为测点流速，u为测点所在垂线平均流速）。由Fluent数值模拟结果分析可得：对于明渠壁面区域（0＜y/h≤0.2）呈对数分布［6］；在半深度区域（0.2＜y/h≤0.6）流速分布符合抛物线分布［6，7］；在自由水面区（0.6＜y/h≤1）由于二次回流的影响，水面具有波动性，但流速分布也符合抛物线分布。

①壁面区域流速模型

通过Fluent数值模拟结果分析，得到壁面区域流速分布拟合函数为

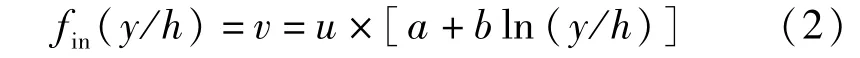
式中：fin（y/h）为壁面区域流速函数；a=1.161 13+ 0.040 15z/h；b=0.125 97+0.051 59z/h；z为垂测线距邻近边壁的距离。

②半深度区域流速模型

式中：fout（y/h）为半深度区域流速函数；

式中：ftra（Z）为横向垂线平均流速函数；u为垂测线平均流速；U为中垂线平均流速；Z垂测线距中心的距离；b为明渠宽度。

3　测量不确定度来源分析

3.1测量仪器引入的不确定度

式中：ucm、ubm、uhm分别为流速仪、宽度测量仪器、水深测量仪器引入的不确定度。

3.2垂线平均流速测量引入的不确定度

垂线平均流速测量与垂线的测点数、测速历时及测速仪重复性因素有关，可得垂线平均流速测量引入的不确定度为［5］

3.4边壁盲区流速插补引入的不确定度

引入横向平均流速分布模型推导边壁盲区的平均流速，则边壁盲区流速影响引入的不确定度为

4　测量数据与处理

明渠流量测量在杭州市质量技术监督检测院的大流量实验室进行，明渠长宽高为20m×1m×1m的矩形槽，测量断面设置在距水流入口10m处，断面上设置3条垂线，采用2点法测量，采用声学多普勒测速仪测量断面流速，磁致伸缩液位计测量明渠水深，各垂线测量使用丝杆定位，测量数据见表1。

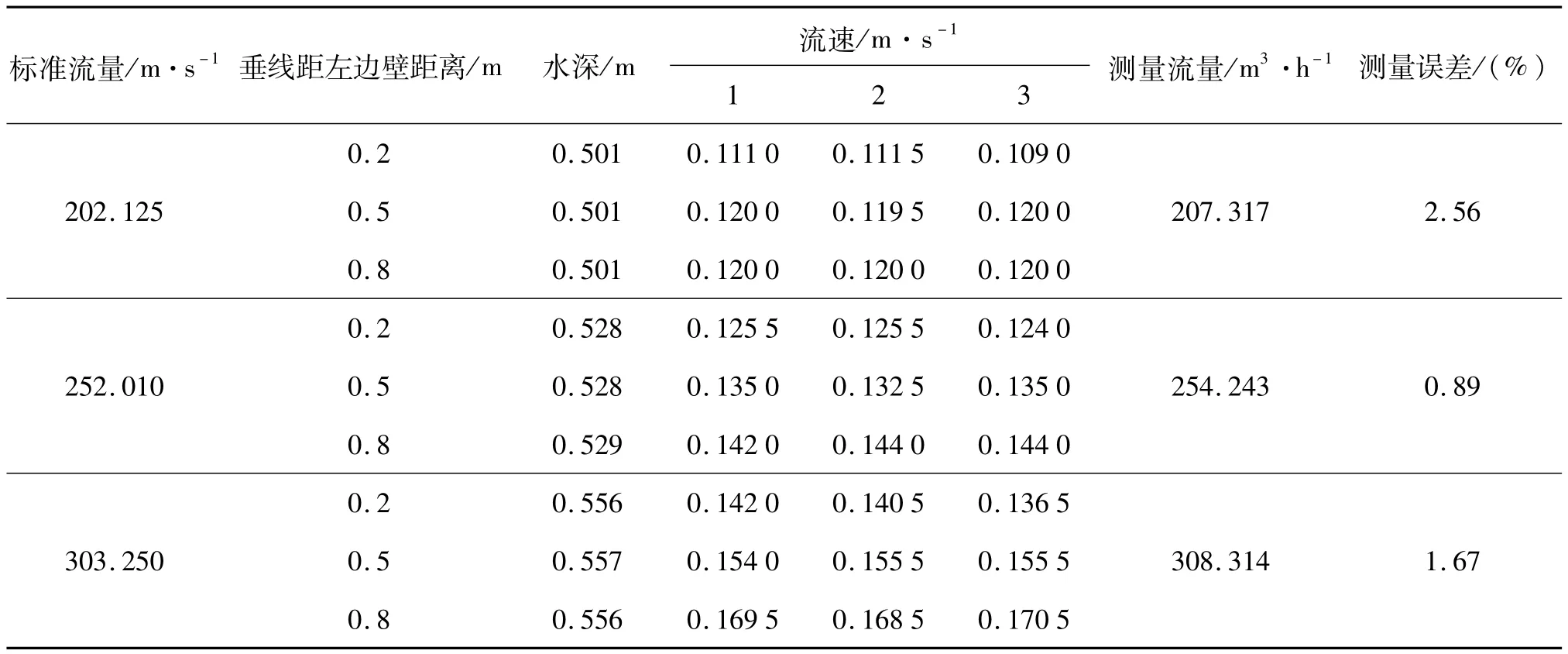
表1　实验测量数据

从表1数据可知，基于流速分布模型计算明渠流量，其误差小于2.56%，满足明渠测量的精度要求。根据贝塞尔公式可得，流速和水深测量重复性引入相对标准不确定度分别为

5　测量标准不确定度评定

5.1合成标准不确定度

通过明渠流量测量不确定度分析，则公式（1）变为

式中：n=2，m=3。

明渠流量测量不确定度分量见表4。

表4　明渠流量测量不确定度分量一览表

根据式（17）可得合成相对标准不确定度为

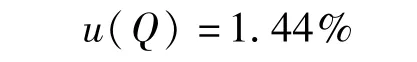
而根据ISO 748提供的数据，计算明渠流量测量合成相对标准不确定度为

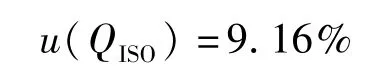
5.2扩展不确定度

选取置信概率P=95%，包含因子k=2，则明渠流量测量相对扩展不确定度为［10］

6　结 语

通过明渠断面的Fluent数值模拟研究，获得了明渠断面流速分布模型，对垂线数、垂线测点不足和边壁流速盲区的不确定度分量进行计算，提出了基于流速面积法明渠流量测量的不确定度评定方法。实验结果表明，该方法能够克服ISO 748对于明渠流量测量不确定度评定的局限性，减少了断面垂线数和测点数，提高了测量的效率及评定的准确性和可靠性。

［1］ Pelletier P M.Uncertainties in the single determination of river discharge：a literature review［J］.Canadian Journal of Civil Engineering，1988，15：834-50.

［2］ Simpson M R.Discharge measurement using a broad band acoustic Doppler current profiler［R］.United States Geological Survey，Open File Report，2001，50-53.

［3］ Le Coz J，Camenen B，Peyrard X.Uncertainty in openchanneldischargesmeasuredwiththevelocity-area method［J］.Flow Measurement and Instrumentation，2006，26：18-29.

［4］ Nezu I，Nakagawa H.Turbulence in Open Channel Flows［J］.Journal of Hydraulic Engineering，1993，120（10）：1234-1237.

［5］ ISO 748—2007.Hydrometry-measurement of liquid flow in open channels using current-meters or floats［S］. 2007.

［6］ 孙东坡，王二平，董志慧，等.矩形断面流速分布的研究及应用［J］.水动力学研究与进展，2004，19（2）：144-152.

［7］ 胡云进，万五一，蔡甫款，等.窄深矩形断面明渠流速分布的研究［J］.浙江大学学报（工学版），2008，42（1）：83-88.

［8］ 张海滨，王中宇，刘智敏.测量不确定度评定的验证研究［J］.计量学报，2007，28（3）：193-197.

［9］ 谢少锋，陈晓怀，张勇斌.测量系统不确定度分析及其动态性研究［J］.计量学报，2002，23（3）：237-240.

［10］崔孝海，区璐.蒙特卡罗方法在微波功率测量不确定度分析中的应用［J］.计量学报，2008，29（1）：77-79.

Uncertainty Evaluation of Open-channel Discharges Measurement with the Velocity-area Method

ZHAO Wei-guo1， WANG Cheng-li1， ZHU Wei2， DAI Liang-chao1
（1.China Jiliang University，Hangzhou，Zhejiang 310018，China； 2.Hangzhou Institute of Calibration and Testing for Quality and Technical Supervision，Hangzhou，Zhejiang 310019，China）

According to the ISO 748，when the uncertainty of open channel discharge measurement was evaluated，the sufficient measurements and verticals need be set in the cross-section，but velocity interpolation to the edge and in the top/ bottom layers are not taken into account.In order to solve the problems，a new approach is introduced for evaluating the uncertainty.The vertical velocity and transversal mean velocity distribution model of cross-section were achieved with FLUENT.In the experiment，the uncertainty caused by limited number of velocity measurements points and measurement verticals were computed with the velocity distribution models respectively.The uncertainty components are analyzed to calculate the uncertainty of discharge measurements.The experiment results showed that the method improves the accuracy of the measurement uncertainty.

metrology；flow measurement；open-channel；numerical simulation；uncertainty；velocity distribution model

TB937

A

1000-1158（2015）05-0526-04

10.3969/j.issn.1000-1158.2015.05.17

2013-07-24；

2013-11-28

浙江省重点科技团队创新项目（2011R09024）

赵伟国（1973-），男，陕西蓝田人，中国计量学院副教授，主要从事流量检测与智能仪表方面的研究。zjufriendly@163.com