用图解法求解渠道中正常水深的研究
刘凤阳
(辽阳市灯塔市水务局西马峰水利工作站,辽宁 灯塔111302)
1 概 述
辽阳地区田间配套工程星罗棋布,无数渠道断面的设计中求渠道的正常水深h 用明渠均匀流公式:

进行需通过试算求解,工作相当繁琐。例如在西岗村的旱改水的渠道断面设计中由已知的水力要素求正常的水深h,技术人员经过10 余个小时的反复试算才求得正常水深值,弄得头昏脑胀,可谓费时费力,工作效率极低。那么能不能找出一种简便方法,不通过试算就能准确的迅速的解决问题,从而提高工作效率[1-3]。
2 渠道中正常水深图解法求值
当渠道中的各水力要素如渠道坡降i,渠床糙率n 边坡比系数m,底宽b,已确定的情况下有流量存在时便有一个对应的正常水深存在,也就是水深随着流量的变化而改变,流量是变量,正常水深是因变量,这就同曲线函数有着不谋而合的关系,如果把这种关系曲线展绘于图上,通过图解由所设计的流量,求相应的正常水深其方法为设3个渠道水深h 值,由公式:

算出3个相应的流量值,然后,取直角坐标系,横坐标为设计流量值Q,纵坐标为正常水深值h,按一定的比例用展函数图像的方法依次把3 对水深值流量值绘于图上用匀滑的曲线连接起来便得到了关于Q ~h 的关系曲线然后根据所设计的流量,从图中迅速的查出对应的正常水深值[4-5]。
3 实例说明
如某一地区其渠道设计流量Q 为0.8 m3/s,该地区土质为重壤土m =1(其边坡比为1∶1)考虑坡降,和上下流水位的要求确定渠底坡降i 为1/1000,根据土质情况所查资料选用的渠床糙概率n 为0.0225,为了节省土地其渠底宽度b 为0.8 m,试求正常水深值。

求出相应的Q 值。
1)设水深h1=0.6m,则由:
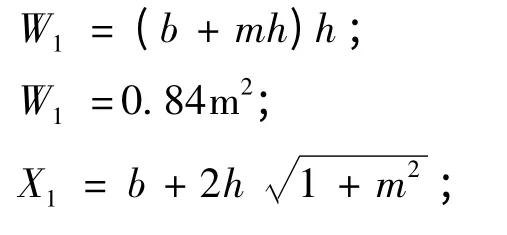
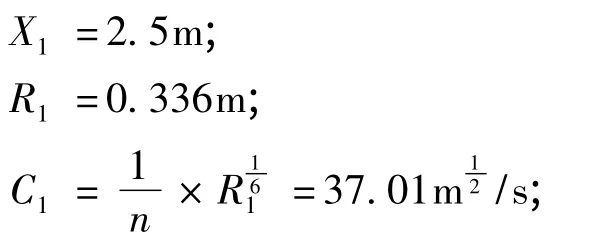
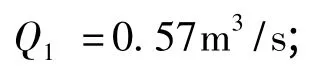
由Q1=0.57 m3/s <Q =0.8 m3/s,说明h1设小了。
2)设h2=0.8 m,则:
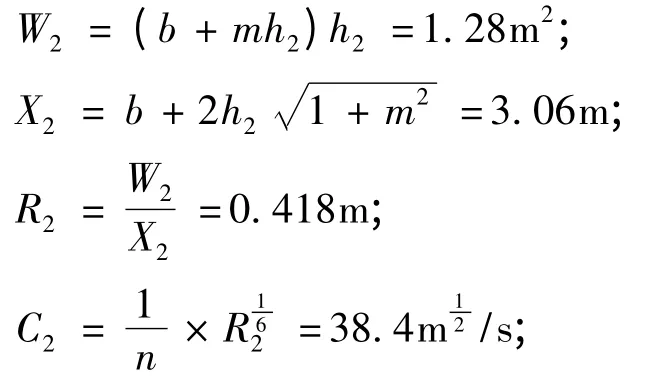
则Q2=1.0049 m3/s;
由Q2=1.0049m3/s >Q =0.8m3/s,说明h2设小了。
3)设h3=0.7 m则
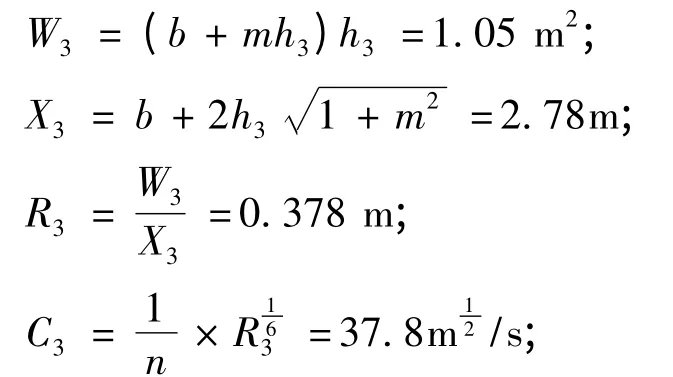
则Q3= C3× W3即:
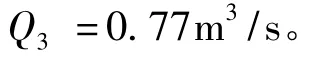
由以上所设h 值及所设Q 值做关于Q ~h 关系曲线图如图1。
由图上可知当Q =0.8 m3/s时的正常水深h 值为0.715 m。
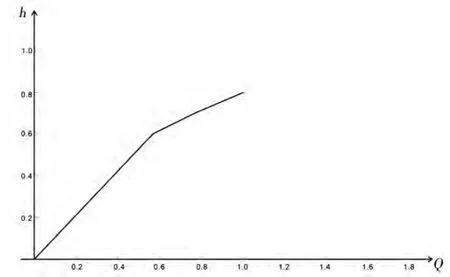
图1 Q ~h 关系曲线图
4 结 论
由以上结论可知在各水力要素已定的情况下利用图解法可准确迅速的求出正常水深从而提高工作的效率。同时,利用图解法求水深时即设的水深值至少为3个且在做图时一定要认真准确。
[1]李蕊. 梯形明渠特征水深直接计算方法研究[D]. 西安:西北农林科技大学,2008.
[2]王正中,陈涛,万斌,申永康. 明渠临界水深计算方法总论[J]. 西北农林科技大学学报:自然科学版,2006(01):161-167.
[3]吕宏兴,辛全才,花立峰. 马蹄形过水断面正常水深的迭代计算[J]. 长江科学院院报,2001(03):8-11.
[4]王正中,宋松柏,王世民. 弧底梯形明渠正常水深的直接算法[J]. 长江科学院院报,2005(03):13-15.
[5]王正中,席跟战,宋松柏,王耀光. 梯形明渠正常水深直接计算公式[J]. 长江科学院院报,1998(06):2-4,8.

