Silicon isotope fractionation during the precipitation of quartz and the adsorption of H4SiO4(aq)on Fe(III)-oxyhydroxide surfaces
Hong-tao He·Yun Liu
Silicon isotope fractionation during the precipitation of quartz and the adsorption of H4SiO4(aq)on Fe(III)-oxyhydroxide surfaces
Hong-tao He1,2·Yun Liu1
Equilibrium Si isotope fractionation factors among orthosilicic acid(i.e.,H4SiO4(aq)),quartz and the adsorption complexes of H4SiO4(aq)on Fe(III)-oxyhydroxide surface werecalculated using the full-electron wave-function quantum chemistry methods[i.e.,B3LYP/6-311G(2df,p)]with a new cluster-model-based treatment.Solvation effects were carefully included in our calculations via water-droplet method combined with implicit solvent models(e.g.,PCM). Theresultsrevealedthat,ifitisunderequilibriumconditions,heavy Si isotopeswould besignificantlyenrichedinquartzin comparison to H4SiO4(aq).However,most of the field observations suggested that quartz would have identical or even depleted δ30Si values compared to that of H4SiO4(aq).To explain this discrepancy between the equilibrium calculation results and the field observations,the kinetic isotope effect(KIE)associated with the formation of amorphous silica,which usually is the precursor of crystalline quartz,was investigated using quantum chemistry methods.The KIE results showed that amorphous silica would be significantly enriched in light Si isotopes during its formation.Our equilibriumfractionationresults,however,matchedaspecialtype of quartz(i.e.,Herkimer‘diamond'')very well,due to its nearly equilibrated precipitation condition.Opposite to the case of precipitated quartz,a large equilibrium Si isotope fractionation(i.e.,-3.0‰)was found between the absorbed bidentateSisurfacecomplexes(i.e.,2C>Fe2O2Si(OH)2)and H4SiO4(aq).This calculated equilibrium Si isotope fractionationfactorlargelydifferedfromapreviousexperimentalresult(ca.-1.08‰).We found that the formation of transient or temporary surface complexes[e.g.,1V>Fe2OSi(OH)3]may have accounted for the smaller net fractionation observed. With the equilibrium and kinetic Si isotope fractionation factors provided here,the distributions and changes of Si isotope compositions in the Earth's surface systems can be better understood.
Si isotope·Equilibrium isotope fractionation·Kinetic isotope fractionation·Adsorption complexes·Fe(III)-oxyhydroxide·Quartz
1 Introduction
Silicon has a high crustal abundance,27.72%,which is only second to that of oxygen(Clarke and Washington 1924)and extensively takes part in the material cycling of spheres.Silicon has three stable isotope,28Si,29Si and30Si.Typically,the silicon isotope compositions of samples are expressed as the deviation(in terms of‰)of the ratio of30Si/28Si from the standard sample(NBS-28 or Rose Quartz),noted as δ30Si{δ30Si=[(30Si/28Si)sample/(30Si/28Si)standard-1])×1000‰}.Duetotherecent high precision of MC-ICP-MS(superior to 0.1‰ δ30Si)anditsrelativelylargeisotopicvariations,11.8‰(Opfergelt and Delmelle 2012),in Earth's surface environments,the Si isotope compositions in many of Earth's surface systems including soils,rivers,oceans,silicon-accumulating algae and high plants have been investigated(Basile-Doelsch et al.2005;Ding et al.2008,2009;Georg et al.2007,2009;Hughes et al.2013;Ziegler et al.2005a,b).Comprehensive reviews of Si isotope geochemistry can be found in Opfergelt and Delmelle(2012).In general,river water and sea water have positive δ30Si signals,but ground water and secondary minerals have negative ones.
Previous studies suggested that the Si isotope distribution in the Earth's surface environments resulted from the preferential release of28Si during the mineral dissolution and the preferential incorporation of28Si in the crystal lattices of secondary minerals.In fact,although light Si isotopes will be preferentiallyreleasedduringthedissolution,theleftheavySi isotopes will also be released into the solution as the dissolution progresses.This can eventually cause the solution to inherit the Si isotopic signals of the primary silicate minerals. Ziegler et al.(2005a)conducted dissolution experiments on basalt.The solution was initially expected to be enriched in light Si isotopes,with the trace primary mineralshavingbeen dissolved.Thesubsequentabruptincreaseofδ30Siinsolution substantiates the aforementioned diagnosis.Therefore,the dissolution of primary silicate minerals probably does not cause Si isotope fractionations.
Furthermore,minerals with stronger bonds are expected tobeenrichedinheavyisotopes(e.g.,Schauble2004).Inthis case,quartz has a shorter average Si—O bond length compared to that of an aqueous H4SiO4solution(1.610 vs. 1.639 A°,Hazen et al.1989;Rastsvetaeva et al.2009). Therefore,quartz should be enriched with30Si when it is in equilibrium with the solution,in contrast to the field observations.There must be some unknown processes to change the Si isotope compositions of quartz.
In addition,adsorption-driven Si isotope fractionation is anothereffectthathasnotbeenseriouslyinvestigatedandmay have a big impact on the Si isotope distribution in the Earth's surface environments.Because Fe(III)-oxyhydroxide is ubiquitous on the Earth's surface as a scavenger,Delstanche et al.(2009)studied the Si isotope fractionations during the adsorption of monosilicic acid onto Fe(III)-oxyhydroxide surfaces and revealed that28Si was preferentially adsorbed to thesurfacesandcausedabout-1.08‰fractionationinterms of30/28Si.Silicon and germanium(Ge)havesimilarchemical properties.Inthesolution,theyareboth4-coordinatedspecies(e.g.,H4SiO4and H4GeO4).Li and Liu(2010)calculated the equilibrium Ge isotope fractionation during adsorption onto Fe(III)-oxyhydroxide surfaces and suggested a preferential adsorption of light Ge isotope with a larger isotopic fractionation(-1.7‰)thanwhatwasreportedfortheSiisotopes(Delstancheetal.2009).AccordingtoJohnsonetal.(2004),Si isotopeshavelargerrelativemassdifferencesthanGeisotopes do.It is reasonable to expect larger Si equilibrium isotopic fractionation during the adsorption of H4SiO4on Fe(III)-oxyhydroxide.
In the present study,we calculated the equilibrium Si isotope fractionation factors and the possible Si kinetic isotope fractionation factors during the precipitation of quartz. Meanwhile,tocheckthemagnitudeofequilibriumSiisotopic fractionation between monosilicic acid and the adsorbed Si surface complexes on Fe(III)-oxyhydroxide surface,firstprinciple quantum chemistry methods were also carried out.
2 Theory and calculations
2.1 Bigeleisen and Mayer equation
Bigeleisen and Mayer(1947)and Urey(1947)established the theoretical framework of isotope geochemistry by providing the calculation method for the equilibrium constant for the isotopic exchange reaction.The central idea is about the calculation of the reduced partition function ratio(RPFR)based on the harmonic frequencies of the interested compound and its rare isotope substituted isotopologue.RPFR is defined as

where u=hcω/kT,with h denoting the Plank constant;k,the Boltzmann constant;T,the absolute temperature in Kelvin;c,the velocity of light;and ω,the harmonic frequencies in cm-1.Readers are referred to Schauble(2004)and Liu et al.(2010)for the details of such calculation. Given the RPFRs of a pair of compounds or minerals in equilibrium,the isotopic fractionation factor α can be derived from the ratio of their RPFRs(or β factors)if there is only one isotope substituted:

where A and B denote different compounds or minerals. When only one isotope has been exchanged,the RPFR equals to the β isotope fractionation factor.
2.2 Kinetic isotope effect
Herein,the dimerization of the H4SiO4molecules was designed to mimic the formation of amorphous silica in the Earth's surface environments.There was a large kinetic isotope effect(KIE)in the dimerization processes and therefore must be evaluated carefully.According to Bigeleisen and Wolfsberg(1958),KIE is formulated as the ratio of the rate constants of light and the heavy isotopes in the formation of the transition state complex:

where kLand kHare rate constants for light and heavy isotopes,respectively,and RPFRreactand RPFRtsare the reduced partition function ratios for the reactant and the transition state complex.In the calculation of RPFRts,one of the vibrational degrees of freedom along the path of decomposition was missing from the vibrational partition function(i.e.,becomes 3n-7).Accordingly,RPFRtsis in this form:

2.3 Calculation methods
2.3.1 Geometry optimization of crystalline quartz
In this study,the volume variable cluster model(VVCM)method was employed in the geometry optimization and frequency calculation(Liu 2013).This method is similar to the one proposed by Rustad and co-workers(e.g.,Rustad et al.2010),but modified to improve the isotope fractionation predictions between the solids and solutions.Compared to Rustad et al.'s method,the whole cluster model of mineral now is freely optimized and the same theoretical level is used for both the solid and the solution.
To describe it in detail,the cluster model is built from three dimensional crystal structures established by X-ray diffraction or neutron diffraction data.The interested atom is located at the center of the cluster model.The dangling bonds at the edges(cutting places)is neutralized by adding virtual point charges.For example,if an O—Si bond is cut and the Si atom is removed,several positive virtual charge points will be used to substitute the Si.Their total charge will equal the charge that the removed Si had used when bonding with O(e.g.,+1).Hundreds of virtual charge points were placed by surrounding the cluster model this way.Then,the cluster model's volume and geometry can be adjusted by changing the positions of the virtual charge points to search for its energy minima.All geometry optimization was implemented with the GAUSSIAN09 software package(Frisch et al.2010).For the notoriously soft silicate structures,due to the presence of large tetrahedral member rings,geometry optimization necessitated the addition of extra polarization functions.Therefore,we employed the hybrid DFT method at the B3LYP/6-311G(2df)level to optimize the 3-dimensional structures of silicate minerals(Becke 1993).As for the hydrogen-containing minerals and orthosilicic acid solution,an extra set of p functions was added to this level.Finally,among cluster structures whose volumes were adjustable,the one with the lowest energy after optimization was selected for the RPFR calculation.
The variations of the calculated average Si—O bond lengths by the VVCM method in comparison to the experimental results are given in Table 4.Specifically,the bond length errors compared to the experimental results are less than 0.5%,while the errors of the average bond angle are less than 5%,considerably better than other calculation methods,such as the pseudopotential based planewave function DFT methods.
2.3.2 Solvation effect calculation
We used a hybrid‘explicit plus implicit''solvent model to simulate the solvation effects of aqueous species(e.g.,orthosilicic acid)according to the suggestions from Rustad et al.(2010),i.e.a continuum solvent model was built outside the inner explicit solvent model.To construct the inner explicit solvent model,we followed the‘water-droplet''method used in Liu and Tossell(2005)and Li et al.(2009)to precisely evaluate the solvation effects.An optimized initial cluster consisting of H4SiO4and six water molecules continued to be optimized with an extra six water molecules until the RPFR converged to a certain value.Frequency analyses were taken to confirm that final structures of those‘water-droplets''at least corresponded to the local minima of the energy.To address the effect of the different local configurations,four parallel simulations with different configurations were designed.We used this method to successfully evaluate the solvation effects in the calculation of the B,Ge and Se isotope fractionation factors(e.g.,Liu and Tossell 2005;Li et al.2009;Li and Liu 2010,2011).Finally,water-droplet clusters with twentyfour H2O molecules embedded in PCM-simulated solution were chosen to estimate the solvation effects of this study.
2.3.3 The structure of adsorbed Si complex on Fe(III)-oxyhydroxide surface
The results of X-ray absorption fine structure spectroscopy(XAFS)(Pokrovski et al.2003)and ATR-IR Spectra(Swedlund et al.2010)both indicated that the H4SiO4adsorbed on the Fe(III)-oxyhydroxide was corner-sharing bidentate,i.e.,2C>Fe2O2Si(OH)2.In this study,we rebuilt an edge-sharing Fe(III)octahedral dimer[Fe2(-according to previous studies(Li and Liu 2010 and references therein)for its excellent predicting abilities of the Ge isotopic fractionation during orthosilicic acid adsorption on Fe(III)-oxyhydroxide surfaces.The structure of this dominant edge-sharing Fe(III)octahedral dimer was experimentally confirmed by Pokrovski et al.(2003).The structure of the adsorbed Si surface complex is shown in Fig.1 and the ground state structure has beensearched out.Comparisons of different spin multiplicity energies optimized by two bases are listed in Table 1.
Finally, wechoseacorner-sharingbidentate,2C>Fe2O2Si(OH)2with a multiplicity of eleven to quantify the equilibrium Si isotopic fractionation factor between the orthosilicic acid and the adsorbed Si surface complex on the Fe(III)-oxyhydroxide.
3 Results
3.1 Determination of scaling factor
Due to the existence of anharmonicity in the experimental fundamental frequencies,we determined the scaling factor of the harmonic frequencies by comparing them with those calculated at a much higher theoretical level,such as at the B3LYP/aug-cc-PVTZ level.Table 2 shows the harmonic frequency results of several important modes of H4SiO46H2O at different theoretical levels.Since the central silicon atom hardly moves in symmetric stretching modes,the corresponding harmonic frequencies usually do not change after the Si isotopes substitution,which means symmetric stretching modes will not contribute to the RPFR value. Therefore,we chooe bending and antisymmetric stretching vibrational frequencies to determine the scaling factor. Cluster models using B3LYP/6-311G(2df,p)method can successfully predict the mid range IR adsorption frequencies,which are sensitive to the vibrational modes of Si.The calculated results are comparable to McIntosh et al.(2011)experimental data(939 cm-1for antisymmetric ν(SiO)stretching mode and 787 cm-1for bending mode).Herein,a method of minimizing root-mean-square error(RMSE)?

Fig.1 The optimal structure(S=11)optimized by B3LYP/6-311G(2df,p)

Table 1 The relative electronic energy differences among different spin multiplicities of2C>Fe2O2Si(OH)2
was employed to find the best scaling factor fit(http://en. wikipedia.org/wiki/Root-mean-square_deviation;Wong 1996).

where λ is the frequency scaling factor,is the ith frequency calculated at B3LYP/6-311G(2df,p)level,is the ith frequency calculated at B3LYP/augcc-pVTZ level and N is the number of normal vibrational modes involved.Finally,a scaling factor of 0.98 was obtained using this method.
3.2 RPFRs of aqueous H4SiO4solution
Table 3 shows the calculated RPFRs of the aqueous H4SiO4of different methods.The fluctuation of RPFRs is delineated as the consequence of varied solvation effects due to the different amounts of water molecules added into the outer coordination shell(Table 3).With the increase of water molecules,the RPFR values eventually converged to a certain value(Fig.2).Also,the hybrid method showed its effectiveness in simulating the solvation effects,evidenced by the identical RPFR value with the result of the‘water droplet''method(i.e.,1.0718 vs.1.0717)and the good results in the geometry optimization and vibrational frequency modeling(Tables 4,5).Lastly,we used the average RPFRvalue(1.0718)obtainedbythe‘water-droplet+PCM''methodinlaterisotopefractionation calculations.
3.3 Equilibrium Si isotope fractionation between quartz and solution
Based on the calculated RPFRs,the Si isotope equilibrium fractionation between the quartz and the orthosilicic acid solution at ambient temperatures was not zero(Douthitt 1982)or a large negative value,-1.5‰(Basile-Doelsch et al.2005),but a larger positive value about 3.3‰ at 298.15 K,as depicted in Fig.3.The theoretical curve matches the observed Si isotope fractionation of euhedral quartz precipitated from the hydrothermal fluids(Dai et al. 2004,2005;Douthitt 1982).

Table 2 Bending and antisymmetirc stretching harmonic frequencies calculated by different theoretical levels

Table 3 Calculated RPFRs of aqueous H4SiO4of different methods
3.4 KIE in the dimerization process of orthosilicic acid
The stable reactant and product are depicted in Fig.4.A transition-state complex with a five-coordinated Si was identified using the synchronization transition quasi-Newton searching methods(i.e.,the QST3 method in Gaussian 09).Our previous study showed that either the polymerization or the depolymerization processes of quartz would be extremely difficult,even with the help of electrolytes and H+or OH-ion(Zhang and Liu 2014).The activation energy calculation here shows a higher energy barrier of 135 kJ/mol for the dimerization of H4SiO4molecules,which is in agreement with previous works(McIntosh 2012;Nangia and Garrison 2008;Zhang and Liu 2014)(Fig.4).Moreover,the calculated KIE value of 1.005 suggests that the light Si isotopes were enriched in the transition-state complex,then in the product.
3.5 Si isotope fractionation during H4SiO4adsorption on Fe(III)-oxyhydroxide surface
The optimized structures of aqueous2C>Fe2O2Si(OH)2are shown in Fig.5 and Table 4.Equilibrium Si isotopefractionations predicted by the models with two or four water molecules are slightly different(Table 6).However,their average results are the same.It means the change of solvation effects will be small if there are already four water molecules around the adsoption complex(Fig.5). Therefore,our Si equilibrium isotope fractionation results should be close to the true value.The average 1000ln(α)is -3.0‰,about three times of the value(-1.08‰)as determined by Delstanche et al.(2009).

Fig.2 RPFR values of aqueous H4SiO4calculated at B3LYP/6-311G(2df,p)level
4 Discussion
4.1 Si isotope fractionation between quartz and solution
The equilibrium Si isotope fractionation between the quartz and the orthosilicic acid solution predicted here is largely different from the field observations(e.g.,Basile-Doelsch et al.2005;Heck et al.2011;van den Boorn et al.2010). Because the average Si—O bond length in quartz is much shorter than that in aqueous H4SiO4(i.e.,1.610 vs. 1.639 A°)(Hazen et al.1989;Rastsvetaeva et al.2009),the equilibrium Si isotope fractionation between these two compounds should not be as most of the field observations suggested.The kinetic isotope effect during the formation of quartz may be the cause of such offset.
Usually,an amorphous silica precursor is formed before the formation of final crystalline quartz.In the above KIEcalculation,we find that the KIE associated with the formation of a dimer of H4SiO4,i.e.,an amorphous silica precursor analogue,can let its δ30Si decrease about 5‰at room temperature,suggesting that the final crystalline quartz can have very light Si isotope compositions,if it inherits light Si isotope signals from its amorphous precursor.Note that the 5‰enrichment of light Si isotope is just for the KIE of a single-step polymerization process. The field observations are the final results of multi-steps and multi-causes.It is not reasonable to expect a perfect match between them.

Table 4 Average Si—O bond length of optimized H4SiO4solution,adsorbed Si surface complexes and quartz

Table 5 Comparisons of modeled antisymmetric ν(SiO)stretching mode and symmetric ν(SiO)stretching mode with experimental data(McIntosh et al.2011)

Fig.3 Theoretical Si isotope equilibrium fractionation between quartz and aqueous H4SiO4solution.Experimental data are from Douthitt(1982)(star),Dai et al.(2004,2005)(diamond).The curve is the results of this study
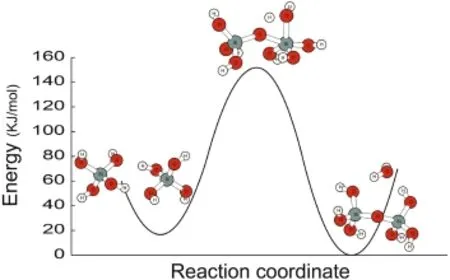
Fig.4 The transition state complex and activation energy for H4-SiO4+H4SiO4dimerization process,at B3LYP/6-311+G(2df,p)level and with solvation effects of PCM method
However,a special kind of quartz,the so-called Herkimer‘‘diamond,''which is extremely pure,is thought to be precipitated under an equilibrium condition.Okamoto and Tsuchiya(2009)suggested that this kind of quartz must be slowly grown in an upward fluid flow to form such a special double-terminated crystal.This also implies a huge solution reservoir for it(e.g.,ruling out isotope reservoir effect).TheknownSiisotopiccompositionofthe Herkimer diamond is very‘‘heavy''and its δ30Si value is +1.4‰ (Rose Quartz as standard sample),which is +1.8‰ heavier than the coexisting hydrothermal fluid(Douthitt,1982).Our equilibrium fractionation result is in good consistence with the result of this special type of quartz(Fig.2).Another line of evidence is that the veined quartzes in the two coal seams precipitated from the lowtemperature hydrothermal fluids had positive a Si isotopic composition:δ30Si=+0.4‰ and+0.6‰ (Dai et al.,2004,2005).Their results are in line with our equilibrium isotope fractionation calculation(Fig.3).Therefore,if quartz is precipitated at equilibrium or near equilibrium conditions,its Si isotope signals will be close to our prediction.Otherwise,the kinetic isotope effects in the amorphous quartz formation processes play the role.
4.2 Si isotope fractionation during H4SiO4adsorption on Fe(III)-oxyhydroxide surface
It is suspected that the equilibrium Si isotope fractionation during the adsorption on Fe(III)-oxyhydroxide surfaces determined by experiments possibly cannot represent the equilibrium fractionation value.The experimental results may be affected by the adsorption of instable Si-surface complexes.To verify our speculation,the Si isotope fractionationbetweenaqueousmonodentate1V>Fe2OSi(OH)3(Fig.6)and aqueous H4SiO4was carefullyinvestigated.We found a relatively smaller Si equilibrium isotope fractionation-1.1‰ (Table 7)compared to the stable bidentate surfacecomplexes.Thismuchsmallerfractionationmatched the experimental results very well.Therefore,the Si isotope fractionation resultsobtained inDelstanche et al.(2009)and Geilert et al.(2014)could possibly represent a result for those transient Si isotope exchanges,where the adsorbed Si complexes were only monodentates,instead of stable bidentates.A longer experiment time is definitely needed to clarify this issue in future.
5 Conclusion
The newly proposed VVCM method is used to calculate several important equilibrium Si isotope fractionation factors among quartz,adsorbed Si on Fe(III)-oxyhydroxide surface and the H4SiO4solution at a decent theoretical level[i.e.,B3LYP/6-311G(2df,p)].The quartz can be enriched with heavier Si isotopes than the H4SiO4solution if it is at equilibrium,up to 3.3‰.Most of the field observations,except euhedral quartz of hydrothermal origin,did not match our calculations for the equilibrium conditions.On the contrary,our KIE calculation results suggested that the light Si isotope enrichment of the field observed quartz was caused by the large kinetic isotopeeffect associated with the formation of amorphous quartz precursor.Meanwhile,the stable absorption surface complexes of H4SiO4(aq)on Fe(III)-oxyhydroxide surfaces were determined and a large equilibrium Si isotope fractionation(~-3.0‰)was found between the adsorbates and the H4SiO4solution,which considerably differed from theexperimental results.Because the transient monodentate adsorption complexes have a Si isotope fractionation very close to the experimental results,we doubt that the experiments were conducted in a quick way,so that the stable bidentate adsorbates even did not have time to form.

Fig.5 Optimized structures of aqueous2C>Fe2O2Si(OH)2at B3LYP/6-311G(2df,p)level

Table 6 Silicon equilibrium isotope fractionation between aqueous2C>Fe2O2Si(OH)2and H4SiO4solution with two or four water molecules nearby

Fig.6 Optimized structures of aqueous1V>Fe2OSi(OH)3at B3LYP/6-311G(2df,p)level

Table 7 RPFR values and silicon equilibrium isotope fractionation between aqueous1V>Fe2OSi(OH)3and H4SiO4solution
AcknowledgmentsWe are grateful for funding support from the 973 Program(2014CB440904)and the Chinese NSF projects(41490635,41173023,41225012).We thank Prof.Chen Zhu(Indiana University)for the helpful discussion.
Basile-Doelsch I,Meunier JD,Parron C(2005)Another continental pool in the terrestrial silicon cycle.Nature 433:399—402
Becke AD(1993)A new mixing of hartreee-fork and local densityfunctional theories.J Chem Phys 98:1372—1377
Bigeleisen J,Mayer MG(1947)Calculation of equilibrium constants for isotopic exchange reactions.J Chem Phys 15:261—267
Bigeleisen J,Wolfsberg M (1958)Theoretical and experimental aspects of isotope effects in chemical kinetics.Advance in Chemical Physics.1:15—76
Clarke FW,Washington HS(1924)The composition of the Earth's crust.United States Geological Survey Professional Paper 127
Dai S,Li D,Ren D,Tang Y,Shao L,Song H(2004)Geochemistry of the late Permian No.30 coal seam,Zhijin Coalfield of Southwest China:influence of a siliceous low-temperature hydrothermal fluid.Appl Geochem 19:1315—1330
Dai S,Chou C-L,Yue M,Luo K,Ren D(2005)Mineralogy and geochemistry of a Late Permian coal in the Dafang Coalfield,Guizhou,China:influence from siliceous and iron-rich calcic hydrothermal fluids.Int J Coal Geol 61:241—258
Delstanche S,Opfergelt S,Cardinal D,Elsass F,Andre´L,Delvaux B(2009)Silicon isotopic fractionation during adsorption of aqueous monosilicic acid onto iron oxide.Geochemica et Cosmochimica Acta 73:923—934
Ding T,Tian S,Sun L,Wu L,Zhou J,Chen Z(2008)Silicon isotope fractionation between rice plants and nutrient solution and its significance to the study of the silicon cycle.Geochemica et Cosmochimica Acta 72:5600—5615
Ding T,Zhou J,Wan D,Chen Z,Wang C,Zhang F(2009)Silicon isotope fractionation in bamboo and its significance to the biogeochemical cycle of silicon.Geochemica et Cosmochimica Acta.72:1381—1395
Douthitt C(1982)The geochemistry of the stable isotopes of silicon. Geochemica et Cosmochimica Acta 46:1449—1458
Frisc MJ,Trucks GW,Schlegel HB,Scuseria GE,Robb MA,Cheeseman JR,Scalmani G,Barone V,Mennucci B,Petersson GA,Nakatsuji H,Caricato M,Li X,Hratchian HP,Izmaylov AF,Bloino J,Zheng G,Sonnenberg JL,Hada M,Ehara M,Toyota K,Fukuda R,Hasegawa J,Ishida M,Nakajima T,Honda Y,KitaoO,Nakai H,Vreven T,Montgomery JA,Peralta Jr JE,Ogliaro F,Bearpark M,Heyd JJ,Brothers E,Kudin KN,Staroverov VN,Keith T,Kobayashi R,Normand J,Raghavachari K,Rendell A,Burant JC,Iyengar SS,Tomasi J,Cossi M,Rega N,Millam JM,Klene M,Knox JE,Cross JB,Bakken V,Adamo C,Jaramillo J,Comperts R,Stratmann RE,Yazyev O,Austin AJ,Cammi R,Pomelli C,Ochterski JW,Martin RL,Morokuma K,Zakrzewski VG,Voth GA,Salvador P,Dannenberg JJ,Dapprich S,Daniels AD,Farkas O,Foresman JB,Ortiz JV,Cioslowski J,Fox DJ(2010)Gaussian 09(Revision C.01).Gaussian,Inc.,Wallingford
Geilert S,Vroon PZ,Roerdink DL,Van Cappellen P,van Bergen MJ(2014)Silicon isotope fractionation during abiotic silica precipitation at low temperature:Inferences from flow-through experiments.Geochemica et Cosmochim Acta 142:95—114
Georg R,Reynolds B,West A,Burton K,Halliday A(2007)Silicon isotope variations accompanying basalt weathering in Iceland. Earth Planet Sci Lett 261:476—490
Georg R,Zhu C,Reynolds B,Halliday A(2009)Stable silicon isotopes of groundwater,feldspars,and clay coatings in the Navajo Sandstone aquifer,Black Mesa,Arizona,USA.Geochemica et Cosmochimica Acta 73:2229—2241
Hazen R,Finger L,Hemley R,Mao H(1989)High-pressure crystal chemistry and amorphization of α-quartz.Solid State Commun 72:507—511
Heck PR,Huberty JM,Kita NT,Ushikubo T,Kozdon R,Valley JW(2011)SIMS analyses of silicon and oxygen isotope ratios for quartz from Archean and Paleoproterozoic banded iron formations.Geochemica et Cosmochimica Acta 75:5879—5891
Hughes H,Sondag F,Santos R,Andre´L,Cardinal D(2013)The riverine silicon isotope composition of the Amazon Basin. Geochemica et Cosmochimica Acta.121:637—651
Johnson CM,Beard BL,Albare`de F(2004)Geochemistry of nontroditional stable isotopes.Rev Miner Geochem 55:1—24
Li XF,Liu Y(2010)First-principle study of Ge isotope fractionation during adsorption onto Fe(III)-oxyhydroxide surfaces.Chem Geol 278:15—22
Li XF,Liu Y(2011)Equilibrium Se isotope fractionation parameters:a first-principles study.Earth Planet Sci Lett 304:113—120
Li XF,Zhao H,Tang M,Liu Y(2009)Theoretical prediction for several important equilibrium Ge isotope fractionation factors and the geological implication.Earth Planet Sci Lett 287:1—11
Liu Y(2013)On the test of a new volume variable cluster model method for stable isotopic fractionation of solids:Equilibrium Mg isotopic fractionations between minerals and solutions. Goldschmidt 2013 Conference Abstracts 1632
Liu Y,Tossell JA(2005)Ab initio molecular orbital calculations for boronisotopefractionationsonboricacidsandborates. Geochemica et Cosmochimica Acta.69:3995—4006
Liu Q,Tossell JA,Liu Y(2010)On the proper use of the Bigeleisen—Mayer equation and corrections to it in the calculation of isotopic fractionation equilibrium constants.Geochemica et Cosmochimica Acta 74:6965—6983
McIntosh GJ(2012)A theoretical kinetic model of the temperature and pH dependent dimerization of orthosilicic acid in aqueous solution.Phys Chem Chem Phys 14:996—1013
McIntosh GJ,Swedlund PJ,So¨hnel T(2011)Experimental and theoretical investigations into the counter-intuitive shift in the antisymmetric ν(Si—O)vibrational modes upon deuteration of solvatedsilicicacid(H4SiO4).PhysChemChemPhys 13:2314—2322
Nangia S,Garrison BJ(2008)Reaction rates and dissolution mechanisms of quartz as a function of pH.J Phys Chem A 112:2027—2033
Okamoto A,Tsuchiya N(2009)Velocity of vertical fluid ascent within vein-forming fractures.Geology 37:563—566
Opfergelt S,Delmelle P(2012)Silicon isotopes and continental weathering processes:assessing controls on Si transfer to the ocean.CR Geosci 344:723—738
Pokrovski GS,Schott J,Farges F,Hazemann J(2003)Iron(III)-silica interaction in aqueous solution:insights from X-ray absorption fine structure spectroscopy.Geochemica et Cosmochimica Acta 67:3359—3573
Rastsvetaeva RK,Chukanov NV,Zadov AE(2009)Refined structure of afwillite from the northern Baikal region.Crystallogr Rep 54:418—422
Rustad JR,Casey WH,Yin Q-Z,Bylaska EJ,Felmy AR,Bogatko SA,Jackson VE,Dixon DA(2010)Isotopic fractionation of Mg2+(-aq),Ca2+(aq),and Fe2+(aq)with carbonate minerals.Geochemica et Cosmochimica Acta 74(22):6301—6323
Schauble EA(2004)Applying stable isotope fractionation theory to new systems.Rev Miner Geochem 55:65—111
Swedlund PJ,Miskelly GM,McQuillan AJ(2010)Silicic acid adsorption and oligomerization at the ferrihydrate—water interface:interpretation of ATR-IR Spectra based on a model surface structure.Langmuir 26:3394—3401
Urey HC(1947)The thermodynamic properties of isotopic substances.J Chem Soc(London)85:562—581
Van den Boorn SHJM,van Bergen MJ,Vroon PZ,de Vries ST,Nijman W(2010)Silicon isotope and trace element constraints on the origin of~3.5 Ga cherts:implications for Early Archaean marine environments.Geochemica et Cosmochimica Acta 74:1077—1103
Wong MW (1996)Vibrational frequency prediction using density functional theory.Chem Phys Lett 256:391—399
Zhang ST,Liu Y(2014)Molecular-level mechanisms of quartz dissolution under neutral and alkaline conditions in the presence of electrolytes.Geochem J 48:189—205
Ziegler K,Chadwick OA,Brzezinski MA,Kelly EF(2005a)Natural variations of δ30Si ratios during progressive basalt weathering,HawaiianIslands.GeochemicaetCosmochimicaActa 69:4597—4610
Ziegler K,Chadwick OA,White AF,Brzezinski MA(2005b)δ30Si systematics in a granitic saprolite,Puerto Rico.Geology 33:817—820
10.1007/s11631-015-0068-0
11 April 2015/Revised:9 July 2015/Accepted:30 July 2015/Published online:8 August 2015
✉ Yun Liu
liuyun@vip.gyig.ac.cn
Hong-tao He
hehongtao0818@yeah.net
1State Key Laboratory of Ore Deposit Geochemistry,Institute of Geochemistry,Chinese Academy of Sciences,Guiyang 550002,China
2University of Chinese Academy of Sciences,Beijing 100049,China
©Science Press,Institute of Geochemistry,CAS and Springer-Verlag Berlin Heidelberg 2015
- Acta Geochimica的其它文章
- Chemical weathering and CO2consumption of a high-erosion-rate karstic river:a case study of the Sanchahe River,southwest China
- Study of an Early Silurian-Early Permian paleo-weathering profile in Zunyi,north Guizhou Province,China
- Geochemical and geochronological studies of the Aketas granite from Fuyun County,Xinjiang:the implications of the petrogenesis and tectonic setting
- Characterization of biochars produced from seven biomasses grown in three different climate zones
- Identification of the four rearranged hopane series in geological bodies and their geochemical significances
- Fluorite REE characteristics of the Diyanqinamu Mo deposit,Inner Mongolia,China

