制动装置能量泄放尖峰电压的研究
钟颖,汪光森,潘启军,欧阳斌,易成霖
(海军工程大学舰船综合电力技术国防科技重点实验室,武汉430033)
制动装置能量泄放尖峰电压的研究
钟颖,汪光森,潘启军,欧阳斌,易成霖
(海军工程大学舰船综合电力技术国防科技重点实验室,武汉430033)
大转动惯量电机实现快速停车需要制动装置配合,直流母线电缆的寄生电感与制动装置直流支撑电容匹配不合理时,容易在直流支撑电容上产生尖峰电压,严重影响制动装置对母线电压的准确调节。针对一种大功率瞬时耗能的制动装置,在考虑电路杂散参数基础上,利用拉普拉斯变换建立系统运算电路模型,通过电路暂态过程分析,推导出直流支撑电容电压振幅的表达式。改变电路中影响电压振幅的参数,进行仿真和实验,验证了理论分析和仿真计算的正确性。
制动装置运算电路滞环控制尖峰电压
0 引言
三相异步电机有多种制动方式,其中常用的电气制动主要包括反接制动、能耗制动、回馈制动[1-3]。反接制动优点是制动效果强,缺点是能量损耗大,制动准确度差。能耗制动主要用于较大容量要求制动平稳和起制动频繁的场合。回馈制动时可以将一部分能量反馈储存在电容上,多余能量通过电阻消耗[4-5]。能量回馈装置系统具有的优越性远胜过能耗制动和反接制动。常用的电机电磁制动不需要能量回馈,而且电机转动惯量较小,电机制动曲线缓慢[6-7],对瞬时制动性能没有特殊要求,因此制动单元以及制动电阻一般安装在逆变器中就能满足制动需求。
但是对于大转动惯量高性能电机制动而言,不仅需要对电机制动时反馈的部分能量进行存储,电机瞬时制动功率也有较高要求,因此需要大功率电阻对多余能量快速释放。为了满足极端工况要求,将制动单元以及制动电阻从逆变器中分离出来做成制动装置。
制动装置与逆变器之间的直流母线电缆的寄生电感与直流支撑电容会相互作用,而且制动装置与逆变器的直流支撑电容都会有尖峰电压产生。本文将研究尖峰电压产生的原因及其对制动装置工作的影响,对可能影响制动装置内电压电流变化的因素进行研究,归纳出电容电压振幅变化规律,通过仿真和实验验证结论。
1 尖峰电压产生
1.1制动过程
本文研究的制动装置原理图如图1所示,直流侧PO、ON对称,Q1、Q2为IGBT,D1、D2为二极管,Cb为直流支撑电容。为减小线路杂散电感,采用复合母排[8]连接IGBT、二极管、直流支撑电容,集成为斩波单元。R1、R2为制动电阻。

图1 制动装置拓扑原理图
制动装置与逆变器通过直流母线电缆连接,逆变器Pinv端到制动装置P端电缆等效阻抗为RL,L为逆变器到制动装置之间电缆的寄生电感,等效电路如图2所示。制动装置采用滞环控制策略[9],当制动装置直流支撑电容电压Ub高于开通阀值Uup时开通制动。开始制动后,Ub低于关断阀值Udown时关断斩波单元。

图2 逆变器与制动装置连接示意简图
斩波单元导通时,电流从P端流入,经过斩波单元IGBT,通过制动电阻R1,从O端流回。斩波单元导通时,此时忽略连接电缆的电阻和寄生电感,逆变器直流支撑电容Cinv与制动装置斩波单元内直流支撑电容Cb等效为并联,并联后电容等效为C1,此时电路可以简化为制动电阻R1与C1串联放电电路。放电时间常数为τ=R1C1。电容上的能量通过制动电阻R1进行泄放。直流支撑电容电压Ub迅速下降,控制器检测Ub低于Udown后,斩波单元关断。
斩波单元内IGBT关断瞬间,根据楞次定律,电缆的寄生电感会产生感应电流,流过电缆千安培级的电流不会立即变为0。可以认为电缆上的电流流向电容Cb,电缆的磁场储能转化为电容的电场储能,从而电容电压Ub升高。由于Cb较小,Ub迅速上升。
考虑控制器开关频率[10],在一个控制周期内,由于电缆寄生电感产生的感应电流流向直流支撑电容,Ub迅速上升,可能会远远超过Uup,甚至达到硬件过压保护阀值,对设备造成严重危害。IGBT关断后最快经过一个周期控制器检测到Ub超过Uup,斩波单元开通泄能,Ub迅速减小,小于Udown后关断斩波单元,激励电缆寄生电感产生的感应电流再次流向制动装置内直流支撑电容,磁场能量转化为电场能量后电容电压Ub升高,当Ub超过Uup时,斩波单元再次开通泄能,如此斩波单元不断开通关断,制动装置直流支撑电容与线路寄生电感不断互相充放电。
斩波单元关断瞬间,电缆寄生电感的感应电流流向制动装置直流支撑电容使得电容电压升高实质是电缆的磁场能量与电容电场能量相互转换的过程。由于Cinv较大,因此逆变器直流支撑电容电压振幅较小,主要研究制动装置直流支撑电容电压的变化规律。
1.2尖峰电压计算
如图2所示,仿照正弦稳态分析中的相量法,用拉氏变换分析线性非时变电路。由于电缆电阻RL较小,忽略RL的压降,对于整个电路有:

设I(s)为电路中电流,斩波单元关断瞬间电感电流为I0,逆变器电容电压为Uinv(0-),制动装置电容电压为Ub(0-),L为电缆寄生电感。

(3)

当三角函数部分取最大值为1时,由于,从而推导出电压振幅的最大幅值计算公式:

可以用来预估斩波单元关断后制动装置直流支撑电容电压的最大振幅。
2 仿真研究
在Matlab中依照图2建立模型仿真,将一台逆变器与一台制动装置用直流母线电缆连接,再在直流侧加上一台充电装置。首先用充电装置将直流母线充电至480V,充电在0.3s内完成,然后断开充电装置。0.5s时给制动装置发送使能信号,此时由于直流母线电压为480V,高于制动装置开通阀值。制动装置内斩波单元导通,对制动装置直流支撑电容进行放电。因为电机制动时,会不断反馈能量到直流母线,制动装置内斩波单元会不断重复开通关断,消耗系统中直流支撑电容上多余的能量。仿真模型可以理解为逆变器已经反馈能量到直流母线上后,装置的工作情况。
仿真参数设置如表1所示:

表1 仿真模型参数
当制动装置检测直流母线电压稳定低于关断阀值后,直流支撑电容放电结束。制动装置电容电压变化以及局部放大图如图3所示,制动装置直流支撑电容电压振幅较大。如果尖峰电压超过设备器件承受范围,会严重危害设备安全。

图3 仿真制动装置电容电压变化
仿真时将逆变器与制动装置连接电缆取15 m长,改变制动装置PO侧电容进行仿真,对比电压幅值变化如图4所示。发现制动装置直流支撑电容电压振幅受电容值影响较大。
将制动装置支撑电容不变,改变制动装置与逆变器之间电缆长度进而改变电缆寄生电感,观察不同寄生电感在制动过程中对电压最大振幅的影响。不同电感值对应的电压振幅如表2所示。用于计算尖峰电压的电感L包括逆变器与制动装置外部连接电缆的寄生电感加上逆变器和制动装置内直流母排的电感2µH。
仿真计算得到的尖峰电压数值与式(5)理论计算得到的数值基本吻合。根据仿真结果可以推断制动装置斩波单元关断后,将激励线路电感与直流支撑电容之间能量的相互转化。

图4 仿真取不同支撑电容值的电压振幅对比

表2 不同距离时电压振幅
3 实验验证
为了验证理论分析与仿真的正确性,进行了验证实验。在其余条件相同情况下,将逆变器与制动装置的直流母线电缆寄生电感取不同数值进行对比验证,三根直流母线电缆摆放成品字形并且尽量保持平直以便于准确仿真出电缆寄生电感。
实验参数可参看表1,用变压整流器将直流母线充电至480V,为了确保安全,断开变压整流供电开关,利用储存在电容里的电能进行静态放电实验。下达制动使能信号可触发滞环控制,制动装置开始工作,对电容进行放电。
首先进行电缆寄生电感为10.5 μH实验,从图5、图6的实验数据中可以观察到PO端电压不断振荡,同时流过制动电阻R1电流在0至2480 A之间变化。说明了斩波单元在放电过程中开关频繁,与理论分析以及仿真现象一致。
此时直流母线电缆寄生电感为10.5 μH,加上制动装置与逆变器柜内直流母排电感2 μH,直流侧寄生电感共为12.5 μH,制动装置直流支撑电容为4 mF,电压最大幅值相比于初始电压增加124V。根据式(7)计算理论最大振幅为111.8V。
直流母线电缆寄生电感为2.1 μH时,制动装置直流支撑电容电压如图7所示:PO端初始电压为460V,开始实验后电压最高达到520V,电压最大增幅为60V,由于电缆寄生电感减小,加上制动装置与逆变器柜内直流母排电感2 μH,直流侧寄生电感共为4.1 μH,此时I0=2000 A,理论电压最大增幅64V。

图5 寄生电感为12.5μHPO端电容电压与电流变化
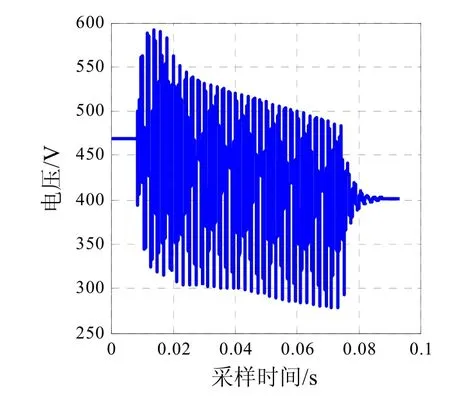
图6 寄生电感为12.5 μH时PO端电容电压

图7 电缆寄生电感为2.1 μH时制动装置PO端电压
直流支撑电容磁场能量不断与电缆电场能转换,流过电容的电流方向不断变化。实验时测量流过制动电阻R1的电流作为I0用于计算。由于电缆实际摆放原因,仿真中电缆寄生电感取值有偏差。因此实验数据与理论计算稍微有偏差,但仍在误差允许范围内,实验结果说明推导的尖峰电压表达式的正确性。
4 结论
本文从高能量瞬态耗能制动装置的制动过程出发,针对制动装置的工作过程,建立电路暂态过程分析的运算电路模型,推导了直流支撑电容尖峰电压幅值的表达式,揭示了制动过程中尖峰电压出现的原因。通过实验进行了验证,并且理论分析、仿真计算与实验数据相吻合。
[1]Klement K,Timborabadi H,EI-Deib A.Closed loop control of a pulsedseries parallel resonant converter with current doubler[C].2010 IEEE International Power Electronics Conference(IPEC),Kokubunji,Japan:IEEE,2010:238-243.
[2]Sukhi Y,Analysis Y,Implementation ofseries parallel resonant converters for regulated powersupply[J]. Joural of the Institution of Engineers India,2010,90(4):18-22
[3]AparnaS,KasirathiN.Seriesparallelresonant converter for electrical discharge matching powersupply[C]2011 1st International Conference on Electrical Energysystems.Beijing,China:2011:28-33.
[4]Bo Yang,Rengang Chen,Fred.Lee.Integrated Magnetic for LLC Resonant Converter.In:IEEE APEC,2002.346-351
[5]Kathryn Klement,Francis Dawson,Steven Thorpe. Resonant converters for pulsed applications[C].2009 13th IEEE European Conference on Power Electronics and Applications.Barcelona,Spain:IEEE,2009:1-8.
[6]胡寿松.自动控制原理(第3版)[M].北京:国防工业出版社,1994.
[7]Hsheng,Y.pei,X.Yang,.Frequency Tracking Control for a Capacitor-Charging Parallel Resonant Converter withPhase-LockedLoop.IEEEAppliedPower Electronics Conference,2007,(1):1287-1292.
[8]林渭勋.现代电力电子电路[M].杭州:浙江大学出版社,2002:204-206.
[9]吴麟.自动控制原理(上下)[M].北京:清华大学出版社,1992:221-230.
[10]王晓明,王玲.电动机的DSP控制-TI公司DSP应用[M].北京:航空航天大学出版社,2004.
Research on OverVoltage of Braking Device
Zhong Ying,Wang Guangsen,Pan Qijun,Ouyang Bin,Yi Chenglin
(National Key Laboratory ofscience and Technology onVessel Integrated Powersystem,Naval University of Engineering Wuhan 430033,China)
Using the braking device to realize rapid braking of a high rotational inertia engine is a normal method.The parasitic inductance of electric cable and direct currentsustain capacitance may cause the capacitorVoltage too high,which makes itVery difficult for brake device to regulate DCVoltage.Taking into accountsomestray parameters,Laplace transformations is applied to build the operational model of thesystem to analyze the transient process.TheVoltage expression of the capacitor is developed.By changing experimental conditions,thesimulation and experimental resultsValidate the correctness of the theoretical analyses andsimulation calculations.
brake device;operational circuit;bang-bang control;overvoltage
TM561
A
1003-4862(2015)10-0017-05
2015-07-26
国家重点基础研究发展计划资助项目(2013CB035601);国家自然科学基金资助项目(51407190);国家自然科学基金资助项目(51477179)
钟颖(1991-),男,硕士研究生。研究方向:电力电子与电力传动。

