“思维可视化”在初中数学教学上的应用

潘朝夕

“思维可视化”在初中数学教学上的应用

潘朝夕

（贵阳市第三十四中学， 贵州 贵阳 550006）

“思维可视化”是指运用一系列图示技术把本来不可视的思维（思考方法和思考路径）呈现出来，使其清晰可见的过程。“思维可视化”在初中数学教学中能展示教学内容，呈现知识结构，体现思维过程，解释数学概念，设计教学过程，实现知识建构，进行教学管理，启发头脑智能。

初中数学；数学教学；思维可视化

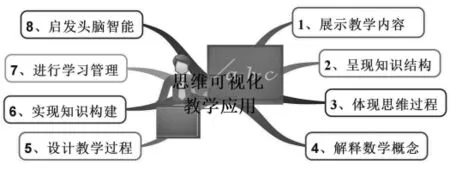
图1

一、展示教学内容

在数学教学过程中，展示知识目标与内容，有利于引导学生掌握学习方向以及基本要求，明确解决学习“学什么”的问题。使用思维导图展示，简单明确，思路清晰，“学什么”一目了然。

例如，“有理数”的知识目标可展示如下图（图2）：

图2

二、呈现知识结构

对教师的教来说，理解初中数学课程标准，通过其知识体系理清结构、归纳重点，是实施教学的关键。对学生的学来说，能够按自己的理解进行整理，用自己的话重新表达知识体系,通过做一个思维导图，形成自己所熟悉的、全面呈现的知识体系，既有利于教学活动的开展，又有利于学生自主学习并掌握。

例如，“初中数学课程标准”呈现如下图（图3）：

图3

三、体现思维过程

训练数学思想和思维过程，是初中数学的一个重要任务。尤其是在数学证明题方面，如果使用思维导图体现证明思路，让所有分析过程的思维可视化，既可以清晰地表达思维走向，又能够寻求解题最佳的解题方法，一举两得，事半功倍。

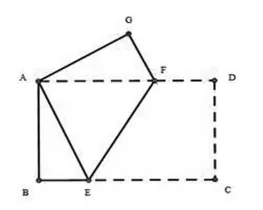
例1，如图4，在正方形ABCD中，F为CD延长线上的一点，CE⊥AF于E，交AD于M。求证：∠MFD=45°

图4

对于这道题，常规的证明过程是这样的：

这样的证明方式，不仅学生的书写过程往往混乱，而且教师的批改也相当费劲。如果根据思维导图对解答进行“分析”（图5），然后再写出证明过程，是不是会更方便学生的理解呢？

图5

在解答题教学上，也同样可以考虑先用思维导图画出解题思路，然后再写出解题过程。

例 2，如图 6，矩形纸片ABCD中，AB=3厘米，BC=4厘米，现将A、C重合，使纸片折叠压平，设折痕为EF。试确定重叠部分△AEF的面积。根据思维导图对解答进行“分析”（图7）：

如图6

图7

答：重叠部分△AEF的面积是4.6875厘米2

四、解释数学概念

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式。正确理解并灵活运用数学概念，是掌握数学基础知识和运算技能、发展逻辑论证和空间想象能力的前提。运用思维可视化技术，既可以帮助学生正确理解，又可以促进学生记忆并灵活运用概念。

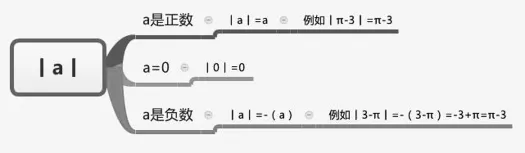
图8

图9

五、设计教学过程

教学设计是教师根据课程标准的要求和教学对象的特点，将教学诸要素有序安排，形成合适的教学方案的设想和计划。一般包括教学目标、教学重难点、教学方法、教学步骤与时间分配等环节。基于思维可视化的教学设计，过程简单易操作，内容清晰方便学。

例如：在认识一元二次方程教学中，一般的教学设计（简案）是这样的：

教学过程：

1.复习回顾

有理数的分类

2.导入新知

（1）同号两数的加法法则

（2）异号两数的加法法则

（3）相反数的加法法则

3.课堂练习

P36随堂练习

4.知识小结

5.作业布置

P36习题2.4

如果画成如下思维导图（图10），看起来应该会更直观一些：

六、实现知识建构

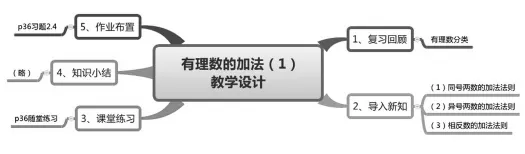
图10

建构主义者认为：客观的知识结构通过个体与之交互作用而内化为认知结构“文化──历史”发展理论等，都是建构主义思想发展的重要基础，为此，通过思维可视图的绘制，实现知识构建，是深刻理解数学知识的必不可少的环节。

例1，实数的分类（图11）：

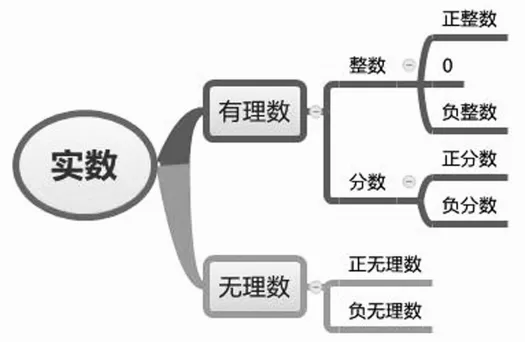
图11

例2，平行四边形、菱形、矩形、正方形的联系（图 12）：

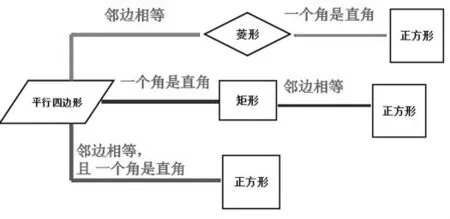
图12

例3，配方法步骤（图13）：

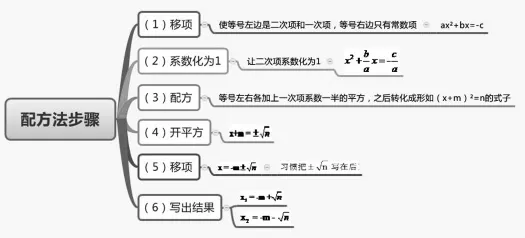
图13

例4，概率的进一步认识（图14）：

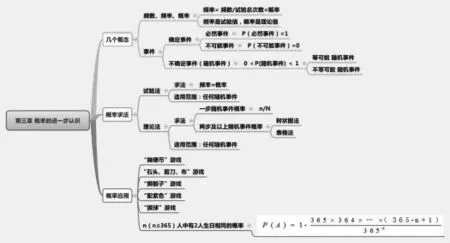
图14

七、进行教学管理

教学管理指利用管理学方法，通过计划、组织、领导、控制等手段，把学习程序化，流程化、规范化、创建更新最佳方案，从而达到高效学习的目的。为了确保学生有效学习，可以通过思维可视化技术制定相应的方案。

例如：2015中考复习计划可制定如下（图15）：

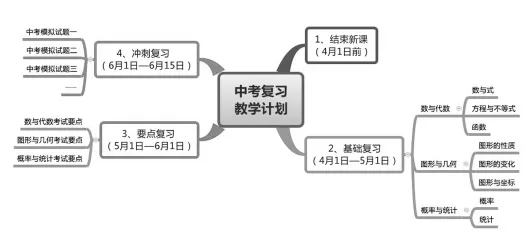
图15

八、启发头脑智能

头脑风暴主要是指无限制的自由联想和讨论，其目的在于产生新观念或激发创新设想。所以又称为智力激励法、BS法、自由思考法等。

例如，在梦想课程《小小加工厂》里，可以设计如下的头脑风暴（图16）：

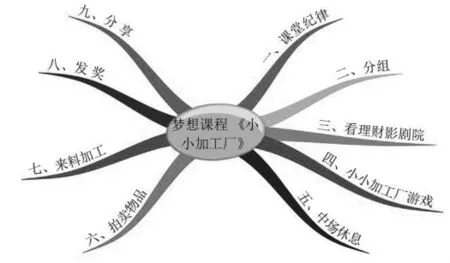
图16

通过近三年的思维导图在数学教学中的应用摸索，本人感觉备课轻松很多，学生学习能力也明显提高，成绩进步较快。

总之，借助思维可视化的教学和学习，对提高教学效果大有好处，应该成为老师们不错的一种教学选择。

[1]中华人民共和国教育部.义务教育教学课程标准[Z].北京师范大学出版社，2011.

[2]刘濯源.赢在学习力[M].万卷出版公司，2008.

The Application of“Thinking Visualization”in Junior High School Mathematics Teaching

PAN Zhao-xi
（Guiyang thirty-fourth middle school,Guiyang Guizhou，550006）

“Visualization”is a process that uses a series of graphic techniques to present the thought that is not visible(thinking and thinking).“Visual thinking”in the junior high school mathematics teaching can display the teaching content,showing knowledge structure,reflects the thinking process,to explain mathematical concepts,teaching design process,knowledge construction,teaching management,inspirebrain intelligence.

Junior middle school teaching；Mathematics Teaching；Thinking visualization

1009—0673（2015）02—0121—04

G633.6

A

2015—02—25

潘朝夕（1968— ），男，贵州安顺人，贵阳市第三十四中学初中数学一级教师，主要研究方向：中学数学。

责任编辑：彭光明

“思维可视化（Thinking visualization）”是指运用一系列图示技术把本来不可视的思维（思考方法和思考路径）呈现出来，使其清晰可见的过程。

思维导图是思维可视化的一种类型，是英国学者东尼·博赞（Tony Buzan）在20世纪70年代所创的表达发散性思维有效的图形思维工具。随着计算机技术的快速发展，通过相关软件就能够完整地将大脑的思维、想法呈现出来。通过绘制思维导图，可以培养学生放射性全面思考问题的习惯，促使学生进行创新性的思考，培养学生的创新能力，而且还是提高学生记忆能力和学习效率的有效工具。

经过笔者在数学教学中利用思维可视化技术的一些实践尝试，“思维可视化”用途很广泛，基本应用可用下列思维导图（图1）表达，可包含8个方面：