基于Sobol指数法作战能力全局敏感性分析方法

尹文进，张静远，饶　喆，冯　炜

（海军工程大学兵器工程系，武汉430033）

基于Sobol指数法作战能力全局敏感性分析方法

尹文进，张静远，饶喆，冯炜

（海军工程大学兵器工程系，武汉430033）

本文采用的 Sobol 指数法，将模型分解为单个参数及参数之间相互组合的函数，通过计算单个输入参数或输入参数集的方差对总输出方差的影响来分析参数的重要性以及参数之间的交互效应。并将Sobol指数法应用于一定作战条件下的鱼雷作战能力分析，探讨了相关关键技术指标及其交互作用对鱼雷作战能力的影响，为鱼雷武器的论证工作提供依据和参考。

Sobol指数作战能力交互影响

0　引言

为了提升武器装备的作战能力，需要对作战能力的影响因素进行分析研究。由于武器装备作战能力分析涉及多个方面因素，但总体可以归纳为武器装备战术技术性能水平和装备作战使用两个方面。在一定的作战使用条件下，由于各个输入因素（武器装备战术技术性能指标）之间的交互作用较为复杂，需要分析各个因素、各个因素组合对武器装备作战能力的影响。传统的作战能力分析方法由于分析因素少、因素变化范围窄、不能分析因素之间的交互作用，不能适应武器装备作战能力分析的需求。而在一定作战使用条件下，Sobol 指数法能够通过分析输入数据和效能输出数据之间的关系，分析各个输入数据与装备作战能力之间的关系，为武器装备论证研究提供依据和参考。

1　Sobol 指数法

俄罗斯数学家 I.M.Sobol于上个世纪 90 年代提出了一种全局敏感性分析方法，并以他的名字命名，学者们称之为“Sobol指数法”[1]。它的核心思想是方差分解，把模型分解为单个参数及参数之间相互组合的函数，通过计算单个输入参数或输入参数集的方差对总输出方差的影响来分析参数的重要性以及参数之间的交互效应。

假设模型为Y=F(X)，其中X=F(x1，x2，…，xn)，xi(i=1,2,…,n)服从[0，1]之间的均匀分布，F(X)平方可积。把模型F(X)分解为以下形式

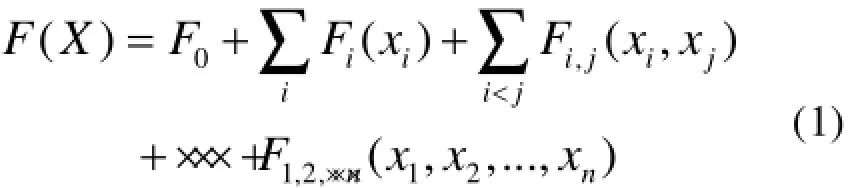
Sobol指数法的研究思路是：用总方差、偏方差分别表示全体变量对输出量的影响、单变量或多变量对输出量的影响情况。其中总方差为偏方差，表示相应的单变量对输出量的影响，偏方差表示输入变量间的相互作用对输出量的影响。如下公式为该算法对方差比率的定义：

采用上述Sobol指数对该模型的敏感性进行度量是否具有理论价值和实践意义，以及如何对定义该指数具体的概念，下面将对此进行讨论。假设函数为 Y=F(X)，其中 X=(X1，X2,… Xn)，(X=1,2,…n)相互独立，而且同时服从同一分布。当 Xi取 xi时函数的条件方差是 V(Y|xi)。V(Y)与V(Y|xi)之间的差值反映出了变量Xi对函数的影响程度。函数为非线性时的某些情况下，V(Y|xi)的数值有可能超出了V(Y)值。为使该算法具有更好地适应性，在变量Xi的有效变化范围内对该变量的条件方差求均值得到EXi(V(Y|xi))。如果EXi(V(Y|xi))很小，说明当变量 Xi为某一取值时，对于函数Y来说，其不确定性很小。换言之，函数Y的不确定性是多源的，但主要是由变量 Xi的不确定性引起的，因此可以得出如下结论：Xi对Y的有较大的影响。根据文献[2]有：

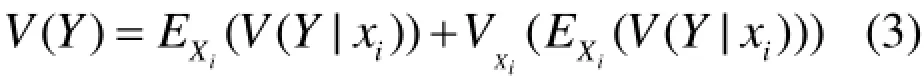
由式(3)知，VXi(EXi(V(Y|xi))越大，则变量 Xi对函数Y的影响程度也就越大。因此Sobol指数法的敏感性指标可以定义为式(4)的形式[3]：

SXi称作Xi的“主效应”指数，也可以称之为一阶敏感性指数，它体现了变量Xi“独自”对函数Y的总方差的贡献程度，其数值的取值范围在[0,1]内。可以根据主效应指数的大小对各个变量进行敏感性排序，主效应指数越大，表明该变量的变化对最终的输出的变化影响也就越大。因此，要控制最终输出的变化，就需要把重点放在控制主效应指数较大的输入量的变化。

若将所有的输入因素分为 Xi和 X-i（除去 Xi因素的其它因素）两类情况。将除Xi之外的所有因素看作为一个整体，VX-i(V(Y|x-i))描述该整体因素对函数Y的方差的综合影响，那么 V(Y)-VX-i(E(Y|x-i))能够表示所有与变量 Xi关联的效应或称之为变量 Xi的“全效应”对函数Y方差的影响程度。因此，敏感性指标可以定义为如式(5)所示的形式[3]：

由于主效应与全效应指数对对应分析函数形式和类型并没有较为特殊的要求，因此该指数的定义适用性较强。如果函数Y=F(X)为武器装备的作战能力函数，Xi为影响作战能力的某个变量。根据和XiS之间的差异表示变量 Xi与其它变量的相互交叉作用对作战能力方差的贡献程度大小。为分析变量i与哪些变量存在较强相互交叉效应时，可根据二者之间的交互效应指数来分析。当分析两个变的相互交叉效应时，VXiXj(E-XiXj(Y|xixj))描述变量Xi和变量Xj作为一个整体对作战能力方差的影响程度。这个影响程度包含变量 Xi与变量 Xj主效应和二者之间的交互效应。因此，

描述了变量Xi与变量Xj的相互交叉效应对作战能力的影响程度大小。因此，交互效应指标可以定义为如式(7)所示的形式[3]：和SXi可知，SXiXj称作变量Xi与变量Xj的二阶交互效应指数。根据同样的原理，可以将三阶交互效应指数SXiXjXk定义为如式(8)所示的形式[3]：

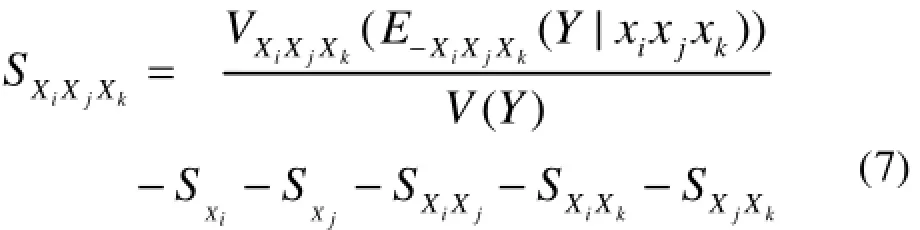
在做相关变量对武器装备作战能力影响程度分析时，如果变量 Xi为影响因素之一，则根据和SXiXj可知表示全部与Xi相关的效应对武器装备作战能力总方差的贡献程度大小，对影响变量的重要性进行排序时，应选择为重要性的评价标准；和XiS之间差异表明变量 Xi与其它变量之间的相互交叉效应对作战能力函数的贡献程度，因此，在分析变量之间的相互交叉效应时，可以根据的大小进行选择分析何种变量；SXiXj表明变量Xi与变量Xj之间的相互交叉效应对武器装备作战能力方差的贡献程度大小，如果SXiXj较大，则可以说明变量Xi和变量Xj之间具有较强的相互交叉效应，两个变量的不同数值组合会对武器装备作战能力的取值有较大的影响；若SXiXj，SXiXk，SXjXk的计算值都比较大，则可以说明变量i是较为关键的变量，且变量i对变量 j和k都有具有一定的作用。综上分析可知，通过和SXiXj的数值分析，不仅可以得到武器装备的关键变量，而且可以获得各个变量之间的相互交叉效应的具体定量化的表述。

3　仿真分析

本文以鱼雷攻击舰船为例，采用Sobol 指数法对鱼雷相关的技术指标进行分析。

鱼雷的基本战技性能指标有：航速、航程、自导作用距离、自导扇面、声脉冲周期、引信作用距离、旋回角速度。为了探寻上述鱼雷武器性能指标的变化对鱼雷作战能力（命中目标概率）的影响，对上述技术指标进行抽样，设计不同的输入变量组合，假定各个输入变量的变化范围如表1所示：

表1　各输入变量取值情况

根据相关的作战模型，采用均匀抽样设计方法，计算不同技术指标的鱼雷命中概率，在此基础上，根据公式（5）、（7）进行Sobol指数的计算，分别得到表2各个输入变量的全效应指数和表3输入变量之间的二阶交互效应如下所示。

表2　各个输入变量的全效应指数

该表中的全效应指数能够表明单变量和其它变量与该单变量之间的相互交叉效应对作战能力（以命中概率为度量指标）的影响。全效应指数较大的变量，表明其全效应及其与其它变量之间的交互效应均较大，即其变化对作战能力变化影响程度较大。由表可得，鱼雷的自导作用距离（X1）的全效应最大。

表3　输入变量之间的二阶交互效应

由表可知，鱼雷自导作用距离（X1）与自导扇面角（X2）之间以及航速（X3）与声脉冲周期（X5）之间存在明显的交互效应，因此在装备论证过程中，应该关注相关性能指标之间的相互关系。

4　结论

本文采用的Sobol将模型分解为单个参数及参数之间相互组合的函数，通过计算单个输入参数或输入参数集的方差对总输出方差的影响来分析参数的重要性以及参数之间的交互效应。通过该方法在鱼雷作战能力分析的应用，探讨了相关关键技术指标及其交互作用对鱼雷作战能力的影响，对鱼雷的论证工作提供一定的参考和依据。

[1] Sobol IM. Sensitivity estimates for nonlinear mathematical models. Math Model ComputExp，1993 : 407-414.

[2] John.A.Rice. 数理统计与数据分析[M]. 北京: 机械工业出版社，2003.

[3] Saltelli，A. et al. Sensitivity Analysis in Pratice: A Guide to Assessing Scientific Models[M]. Chichester: John Wiley and Sons,2008.

[4] 李睿. Sobol灵敏度分析方法在结构动态特性分析中的应用研究 [D]. 长沙: 中南大学，2003.

[5] 徐培德. 军事运筹学基础 [M]. 北京: 国防科技大学出版社，2003.

Global Sensitivity Analysis Method Based on Sobol Index Method

Yin Wenjin，Zhang Jingyuan，Rao Zhe，Feng Wei
(Department of Weapon Engineering，Naval Engineering University，Wuhan 430033，China)

The Sobol index method is used to decompose the model into a function of single parameter and its mutual combination，and the importance of the parameters and the interaction effect between the parameters and the parameters is analyzed by calculating the impact of variance of input parameter. The Sobol index method is applied to the analysis of torpedo operational capability under certain operational conditions，and the influence of the key technical indexes and their interaction on the operational capability is discussed which provides the basis and reference for the demonstration of torpedo weapon.

Sobol index; combat capability; interaction effect

TP27

A

1003-4862（2015）12-0021-03

2015-10-08

尹文进(1988-)，男，博士研究生。研究方向：兵器制导与控制技术。