实战化条件下突击炮射击提前量误差分析
刘俊邦,陈远江,梅 晨,杨 权
(武汉军械士官学校,武汉 430075)
实战化条件下突击炮射击提前量误差分析
刘俊邦,陈远江,梅晨,杨权
(武汉军械士官学校,武汉 430075)
在实战中,地面突击武器将会在高机动状态下与敌进行交战,武器作战效能将会大幅下降。本文通过分析某型突击炮解命中模型误差,建立误差仿真模型,并应用仿真模型计算不同作战条件下的射击提前量误差和命中概率,依据仿真结果分析误差影响规律并提出在实战条件下提高武器作战效能的措施。
实战化突击炮高机动解命中模型射击提前量误差命中概率
0 引言
为适应作战条件变化,突击炮经过多次升级改造后系统性能得到较大提高,但其火控系统的射击理论及实现技术仍延用传统的坦克火控系统相关理论和技术,无法完全满足高速机动的作战要求。以下几方面原因影响了火控系统效能完全发挥:1)简化的解命中模型产生较大解算误差;2)射击延迟对射击精度影响更为突出;3)精确瞄准和跟踪高机动目标难以保证;4)机动中火炮的控制精度和动态过程指标难以保证[1]。
本文试图通过分析交战双方机动条件下影响火控系统性能的主要因素即射击提前量误差,建立误差仿真模型,并应用仿真模型计算不同参数条件下的误差,进而分析误差影响规律并得出在实战条件下提高武器作战效能的措施。
1 射击提前量的解算
1.1解命中模型
解命中模型是火控系统的基本模型之一,其实质是确定弹丸与运动目标在空间相遇点即提前点的坐标,最易受到目标运动影响。
为便于问题研究,建立火炮位置直角坐标系OXYZ,如图1所示。坐标系以火炮发射瞬间炮口位置O为原点;M为发射瞬间的目标位置,m为M在炮口水平面的投影;X轴指向与Om一致;Y轴在炮口水平面内,与X轴垂直并向火炮位置右侧延伸的射线;Z轴过原点O,铅直向上。M为目标现在点位置,D为现在点的斜距,ε为现在点的炮目高低角,β为现在点的方位角(当OX选作基准方向线时,β=0);Mqv为不考虑弹丸附加速度的虚拟命中点位置,mqv为Mqv在炮口水平面的投影,Dqv为虚拟命中点的斜距,εqv为虚拟命中点的炮目高低角,βqv为虚拟命中点Mqv的方位角;Mq为弹丸与目标相遇点,即命中点的位置。
当突击炮在行进间射击时,火炮身管指向虚拟命中点Mqv,弹丸出炮口时载体运动将赋予弹丸一定的附加速度vp0,发射后弹丸与目标的最终相遇点Mq,以弹丸出炮口时刻为零时刻,命中点Mqv的位置可通过以下方程解算:
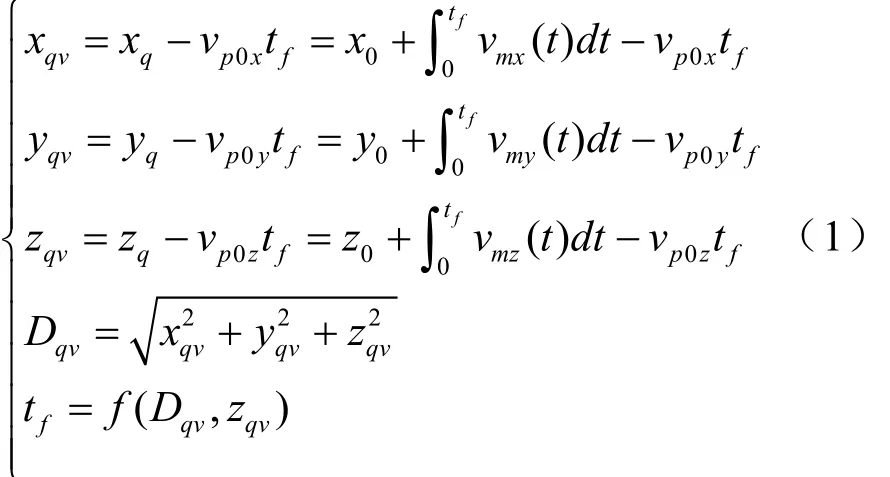
式中:x0、y0、z0为目标现在点位置坐标;vmx、vmy、vmz为目标速度分量;vp0x、vp0y、vp0z为弹丸附加速度分量;xq、yq、zq为命中点位置坐标;xqv、yqv、zqv为虚拟命中点位置坐标;tf为弹丸飞行时间。
在标准条件下对射表数据进行拟合可得到飞行时间函数fn(D),当炮目高低角和斜射程较小时,式(1)中tf可用该函数求解,即:
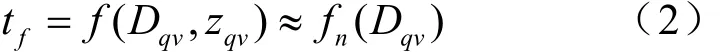
火炮停止间射击时,方程退化为常见的命中模型。
1.2射击提前量计算
如若目标机动,火控系统需以身管当前位置为基准赋予其一定的提前量,方可命中目标。射击提前量包括方向提前量Δβ=βqv-β和高低提前量Δε=εqv-ε,是解命中模型最终求解的物理量。
将解命中方程求解得到的虚拟命中点Mqv和现在点M的坐标进行直角—极坐标系变换、求差、火炮位置—炮塔坐标系变换后既可作为射击诸元装定火炮,火炮位置坐标系下的射击提前量如式(3)所示:
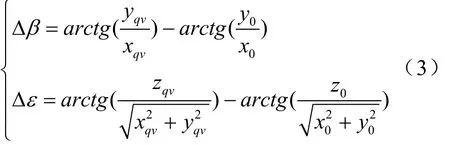
2 高机动条件下射击提前量误差
2.1射击提前量误差分析
火控系统实现中受到工程技术和战场环境等因素的限制,解命中模型经过一系列假设与简化,射击提前量采用式(4)进行计算[2]:

式中:ωβ为目标水平向相对运动角速度,ωε为目标垂直向相对运动角速度。
从式(4)可知,火控系统旨在对弹丸飞行时间和目标相对火炮发射位置的平均相对运动角速度的准确预测来确定射击提前量。而以上两个物理量预测均存在误差:
如图2所示,假设目标在M0点时,进行激光测距获得目标距离数据D0,之后对目标跟踪,经过了系统反应时间Ts后,目标进至Mf点时火炮发射。目标在弹丸飞行时间tf内,行进到相遇点Mq,虚拟相遇点为Mqv。火控系统利用D0通过飞行时间函数预测弹丸飞行时间tfc,而弹丸真实的飞行时间tf与Dqv同样符合飞行时间函数关系,飞行时间估算误差为:
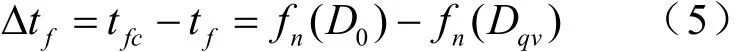
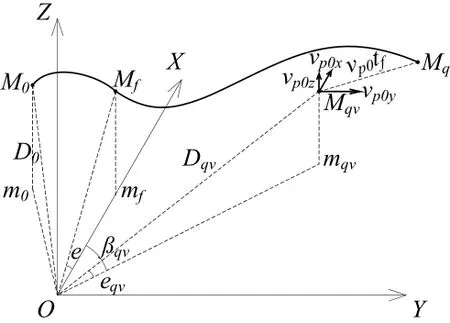
图2 误差示意图
火控系统对击发时刻前两秒内的目标相对运动角速度采样后进行参数估计[3],获得目标平均运动角速度估计值ω,弹丸飞行期内目标相对发射时刻火炮位置的平均相对运动角速度为ωf,目标平均相对运动角速度误差:式中,Δωβ、Δωε为平均相对运动角速度误差,ωβi、ωεi为火控系统对相对运动角速度的采样值,ωβf、ωεf为弹丸飞行期内目标相对火炮发射位置的运动角速度。
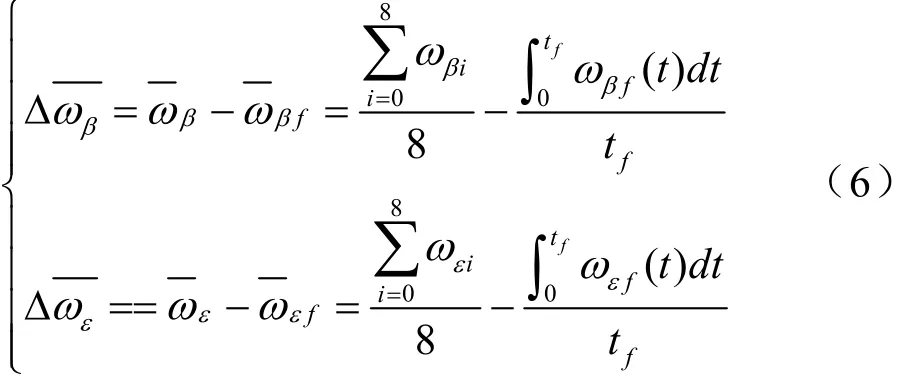
2.2误差仿真模型
误差仿真模型如图3所示,下面阐述主要模型的建模思路。
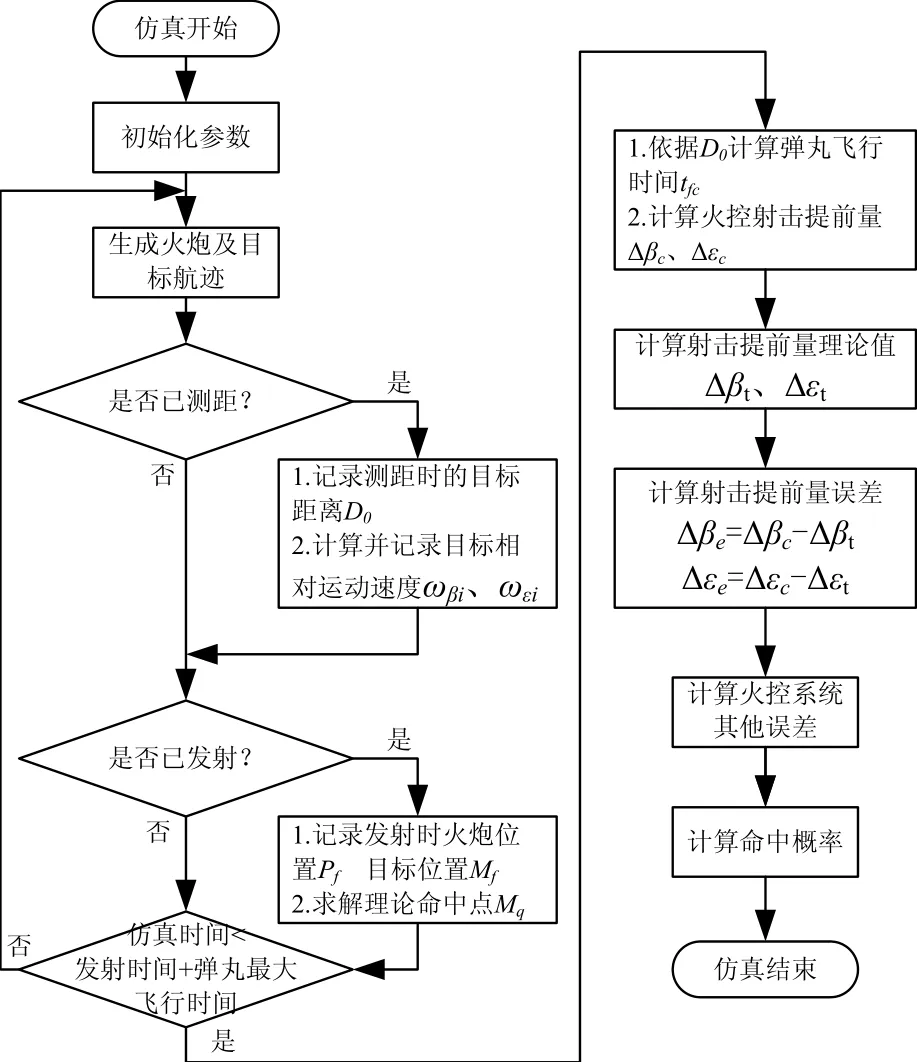
图3 射击提前量误差仿真流程图
2.2.1目标机动模拟
敌我双方运动轨迹可分为直线和曲线两种;加速方式可分为匀速(或静止)、匀加速、变加速三种。无论哪种运动形式,在射击过程中双方的瞬间相互位置关系如图4所示。图4中,OXgYgZg为地面直角坐标系,以仿真开始时火炮所在位置为原点O,OYg与火炮运动方向一致,OXgYg与水平面平行;M0、P0为测距时刻敌我位置;Mf、Pf为发射时刻敌我位置;Mq、Pq为命中时刻敌我位置;φ为目标方位角;λ为目标S形机动的航路角;r为目标S形机动的转弯半径;atg为切向加速度;ang为法向加速度;H为炮目高程差;βm、εm为炮目连线方位角、高低角。 xg、yg为目标位置;vxg、vyg为目标速度;axg、ayg为目标加速度。目标具体运动模型根据atg和ang变化规律确定。

图4 敌我双方运动关系示意图
不失一般性,假设火炮及目标在不同高程的平面内运动,采用曲线运动模型描述目标的运动规律。在直角坐标系下,目标运动模型可以用二阶连续状态方程表示:
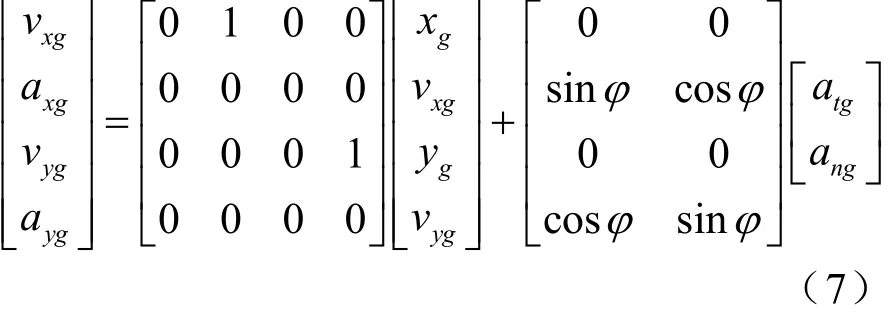
2.2.2火控系统射击提前量解算模拟
依据目标机动模型产生出的目标状态参数,计算目标距离及相对运动角速度。突击炮以固定周期对目标相对运动角速度采样,假设某时刻目标位置为xg、yg、zg,其速度为vxg、vyg、vzg,火炮位置为xpg、ypg、zpg,其速度为vpxg、vpyg、vpzg,此刻目标相对运动角速度为:
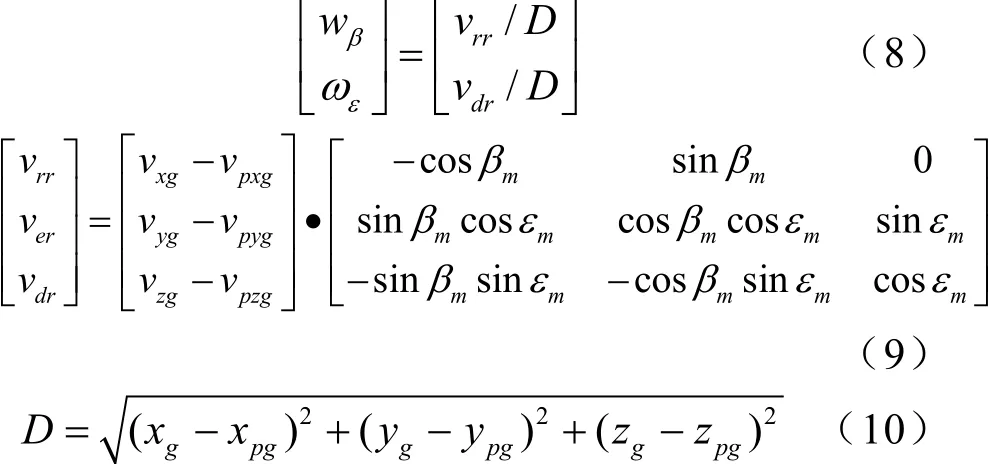
式中vrr、ver、vdr为火炮视线坐标系[4]中的目标相对运动线速度,D为火炮目标距离。对求出的相对运动角速度求算术平均值后,结合飞行时间函数模拟火控系统解算的射击提前量:
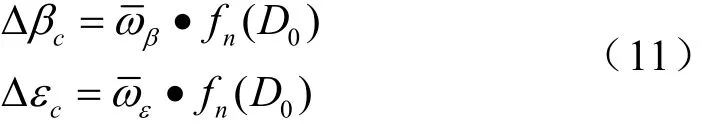
2.2.3射击提前量理论值计算模型
计算射击提前量理论值时,由于非线性方程求解困难,并未直接求取,在仿真过程中缩小距离误差不断逼近命中方程的最优解,其求解过程如下图:

图5 射击提前量理论值求解流程图
由图5可知,随着仿真时间推进距离误差、命中位置以及命中时间不断更新、记录着从发射至当前时间段内目标虚拟距离与相应时间内弹丸飞行距离误差最小时的相关参数,因此仿真结束其数值最接近命中方程的真解。利用命中时目标位置、发射时目标和火炮位置按式(3)计算出地面坐标系下的射击提前量,将其向火炮视线坐标系坐标变换后得到射击提前量的理论值Δβt、Δεt。
3 仿真计算及结果分析
3.1仿真条件
以国外某型主战坦克作为目标的仿真对象,该型坦克最大时速72 km/h,从静止加速至32 km/h用时7 s,采用差速式转向系统可使车辆保持连续的可控的规定转向半径。
火炮及目标运动所在平面高程差低于200 m,火炮在行进间射击时作匀速直线运动,速度范围5 km/h~20 km/h;目标实施S形机动时转弯半径范围10 m ~200 m,速度范围5 km/h~72 km/h,加速度范围0 m/s2~3.0 m/s2,航向角范围为90°~-90°;射击距离范围500 m ~2500m;弹种选择主备穿甲弹。
3.2仿真结果
下面分析目标机动模式、火炮机动模式、火控反应时间、射击距离以及高程差等因素对射击提前量误差及命中概率的影响。
3.2.1目标作匀加速直线机动
取射击距离D0=2000 m,目标初速v0以2 m/s,加速度at以0.5 m/s2为步长进行计算。计算结果如图6所示,误差量随着加速度增加有明显增加,当加速度at=2.5 m/s2,水平提前量误差最大2.74 mil,垂直提前量误差最大为0.14 mil。命中概率随着航路角和目标初速在44.8%~54.6%范围内变化,当航路角为0°的运动目标加速度从0增至2.5 m/s2,命中概率从52.6%下降至45.0%。
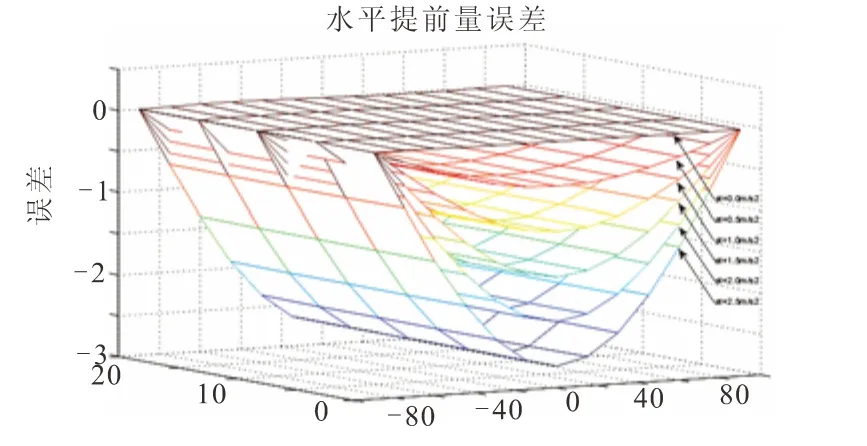
图6目标作均加速直线运动时水平提前量误差图
3.2.2目标作匀加速S形机动
取射击距离D0=2000 m,加速度at=2.5 m/s2,目标初速v0以5 m/s,目标转弯半径r以1 m为步长进行计算。计算结果如图7所示,水平提前量误差最大21.26 mil,垂直提前量误差最大为1.08 mil。命中概率随转弯半径、航路角和目标初速在9.1% ~53.9%范围内变化,受加速度影响较小。目标作小半径(≤20 m)S形机动时,当目标航路角为0°时,命中概率较高,随着目标转弯半径增大,最高命中概率的航路角将不断从0°增加至90°。目标作变加速S形机动,射击提前量误差及命中概率变化规律与目标作匀加速S形机动相似。
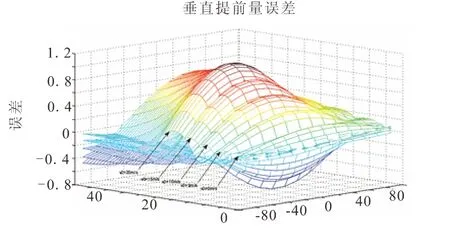
图7 目标作均加速S形时垂直提前误差图
4 结论通过分析仿真结果,本文主要结论如下:
1)比较对不同机动模式目标的射击效果,作S形机动目标射击提前量误差显著高于其他运动形式,命中概率也下降剧烈;
2)目标作非S形机动时,火炮与目标航路夹角为90时,命中概率较高;
3)目标作S形机动时,转弯半径小于20 m时,火炮与目标航路夹角为0时,命中概率较高,随着转弯半径增大,命中概率最高的航路角向-90过渡。
[1] 王钦钊等.兵工自动化[J]. 基于高机动条件下的坦克火控系统,2012,31(3):19-21.
[2] 周启煌. 数字式坦克火控系统基本原理[M]. 北京:兵器工业出版社,1991.
[3] 王钦利等. 火炮发射与控制学报[J].稳像火控系统误差研究,2003,(1):16-18.
[4] 寿少峻等. 火力与指挥控制[J]. 坦克观瞄系统的坐标体系,2006,(5):37-40.
[5] 李光辉等. 计算机仿真[J]. M1A2坦克系统的机动性仿真,2001,(6):4-6.
Analysis of Firing Lead Error for Assault Gun in Actual Combat
Liu Junbang ,Chen Yuanjiang,Mei Chen,Yang Quan
(Wuhan Ordance N.C.O.Academy of P.L.A.,Wuhan 430075,China)
The operational effectiveness of ground assault weapon will decline sharply under condition that the weapon and the target are all in motion in the actual combat. On the base of the analysis of solving hit model error,the error simulation model is built. In addition,the firing lead error and hit probability of the assault gun under different operational conditions are calculated with the error simulation model. Through analyzing the simulation results,the principle of influence on solving hit model error is gained,and the measures to improve operational effectiveness in the actual combat are put forward.
actual combat; assault gun; high-speed; solving hit model; firing lead error; hit probability
TJ37
A
1003-4862(2015)09-0022-04
2015-08-09
刘俊邦(1980-),男,讲师。研究方向:轮式自行火炮装备仿真技术、维修理论与技术。

