软土层几何特性与剪切波速对场地峰值加速度的影响1

刘方成 武景芳 陈 斌 赵成齐

（湖南工业大学土木工程学院，株洲 412008）

软土层几何特性与剪切波速对场地峰值加速度的影响1

刘方成 武景芳 陈 斌 赵成齐

（湖南工业大学土木工程学院，株洲 412008）

软土层对场地地震动的影响一直以来是地震工程学的研究重点。本文应用一维真非线性场地反应分析方法，对某单层匀质场地内软土层的几何特征（厚度与埋深）和剪切波速变化对地面峰值加速度的影响进行了数值分析。研究结果表明：软土层的存在使得场地加速度幅值分布在软土层处发生突变，随着软土层几何特性和剪切波速的不同，这种突变可能使得地面峰值加速度增大或减小；存在一个由软土层厚度、埋深和相对剪切波速三个参数构成的临界状态面，当软土层的状态位于临界面以内时，软土层对地面峰值加速度起放大效应，且加速度效应系数随着上述三个变量的增大表现出先增大后减小的变化规律；当软土层位于临界面以外时，其对地面峰值加速度起衰减效应，加速度效应系数随着上述三个变量的增大而减小。根据算例的参数分析建立了其临界面方程，并提出了估计软土层加速度效应系数的经验公式，可为类似问题提供参考。

软弱土层 场地效应 土动力特性 场地反应分析 地面峰值加速度

刘方成，武景芳，陈斌，赵成齐，2015.软土层几何特性与剪切波速对场地峰值加速度的影响.震灾防御技术，10（4）：840—852. doi：10.11899/zzfy20150403

引言

软夹层对场地反应的影响一直是工程地震学的研究重点。已有的地震灾害调查和场地分析（谢君斐等，1978；钱胜国，1994；黄润秋等，2003；陈国兴等，2004；史丙新等，2010；金丹丹等，2012；张建毅等，2013）均表明，软弱夹层的存在对地表地震反应存在较显著的影响，主要表现为：①软夹层对地表加速度幅值随夹层埋深的不同起到衰减或放大的效果；②含软弱夹层场地的地表加速度反应谱呈多峰值形状，特征周期延长。我国现行抗震规范尚不能敏感地反映软弱土层对场地分类的影响（卢华喜等，2010），可能给工程结构的抗震设计带来不确定性。为修正规范的不足，已有学者在这方面开展了前瞻性的工作，并对软土夹层影响场地效应的机理进行了探索（薄景山等，2003a；2003b；2003c；2004；黄玉龙等，2000）。基于已有研究，本文采用能真实考虑场地土滞回阻尼特性的非线性模型进行真非线性分析，考查了软土层几何构造（厚度和埋深）和剪切波速变化对地表加速度反应幅值的影响规律，并基于参数分析，提出了软土层加速度效应系数的概念及其经验估计公式，为后续研究和规范修订提供参考。

1 计算模型

1.1 含软弱土层场地的构造

鉴于多层土的复杂性，很难看出某一参数对地面加速度反应幅值的影响规律，本文从单层均质场地入手探讨软弱土层的地震效应。假设有一单层匀质场地（II类场地），覆盖层总厚度H=40m，场地剪切波速νs=250m/s，场地土质量密度ρ=2.0×103kg/m3，其中含有一层软弱土层，软弱土层的剪切波速为νss，质量密度为ρi=1.6×103kg/m3，软土层在场地中的几何分布特性由其厚度hL、顶部埋深hT确定。含软土层的场地构造示意图及相关参数取值如图1所示。

1.2 分析程序与计算参数

计算分析在MATLAB语言环境下编制的场地非线性分析程序（FSRAP）中进行。图2给出了程序所采用的一维有限元分析模型（栾茂田等，1992），图中hi、ρi、Gi、Di分别表示第i层子单元的厚度、密度、剪切模量与阻尼比。一维有限元模型各子单元的剪切模量Gi和滞回阻尼比Di随加载时程的变化，由基于阻尼的滞回模型DBM（尚守平等，2007）来模拟。图3给出了FSRAP程序对SHAKE（Idriss等，1992）、NERA（Bardet等，2001）算例的分析结果与SHAKE、NERA计算结果的对比情况。可见，FSRAP程序与SHAKE、NERA计算结果吻合较好，且FSRAP与NERA的结果更为接近，这是由于FSRAP与NERA均为真非线性分析方法，而SHAKE为等效线性方法。而FSRAP与NERA之间的差异则是由于Masing滞回模型不能真实模拟场地土滞回阻尼所致。算例对比分析表明，FSRAP程序具有较好的可靠性。

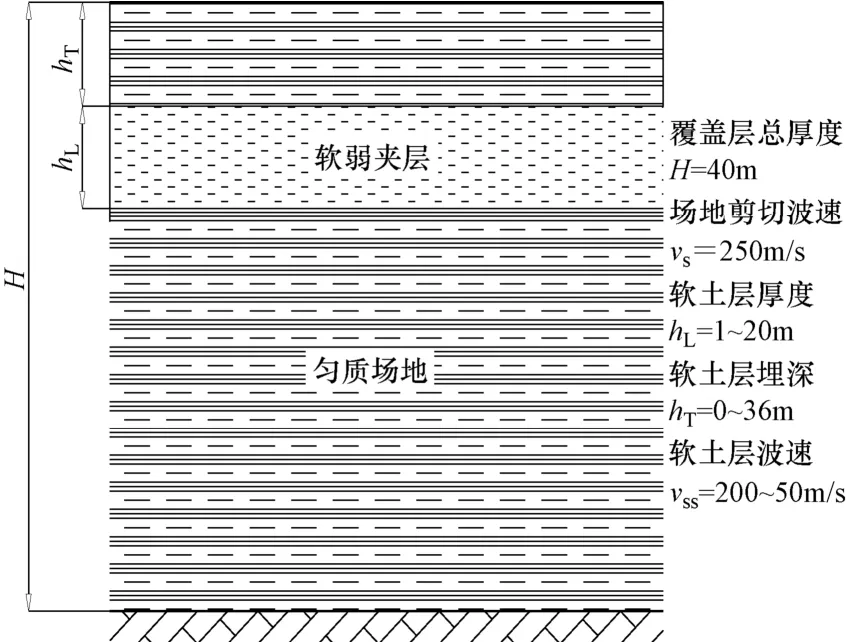
图1 含软弱（夹）层场地剖面构造示意图Fig. 1 Construction diagram of the profile containing a soft soil layer

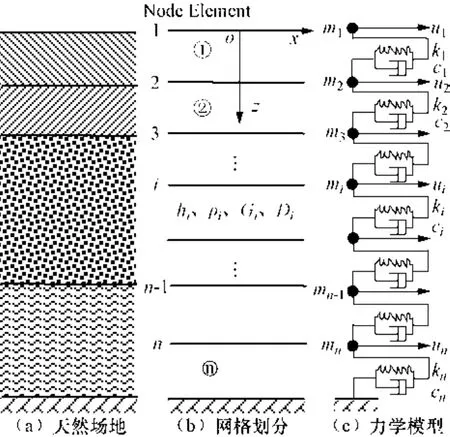
图2 FSRAP一维有限元分析模型Fig. 2 One dimensional analysis model for layered site in the program FSRAP

为尽量减少其他因素的影响，选取Seed等（1970；1986）建议的各类土的经验动力特性曲线（如图4中粗黑线所示）作为场地土及软土共同的动剪模量曲线和阻尼比曲线。分别选取了Taft波、El-centro波、Loma Pretia波作为基岩输入地震波，输入加速度幅值根据不同工况分别调整为0.05g、0.1g和0.2g。不同输入地震波分析结果具有相似的规律，限于篇幅文中仅给出Taft波的计算结果。输入地震波特征如图5所示。

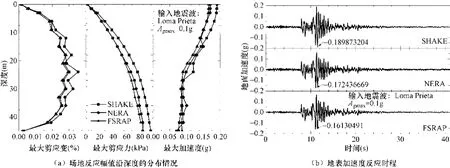
图3 FSRAP与SHAKE、NERA算例分析对比Fig. 3 Comparison of the results from different programs of FSRAP， SHAKE and NERA

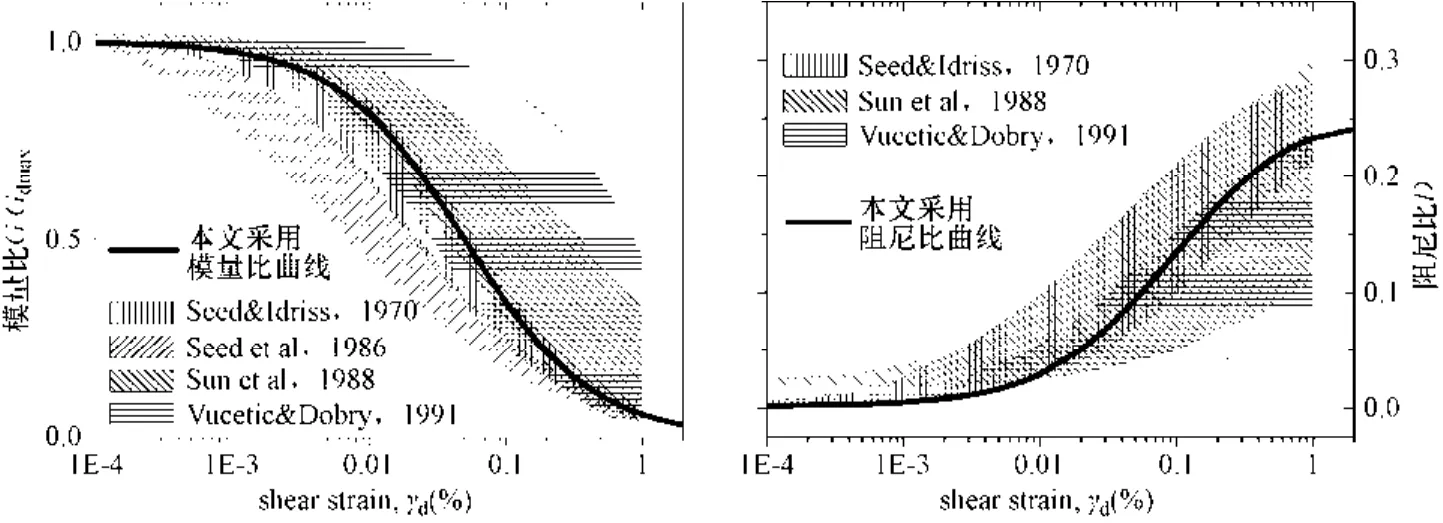
图4 本文计算所采用的场地土动力特性曲线Fig. 4 Dynamic properties curves for selected soil in this study

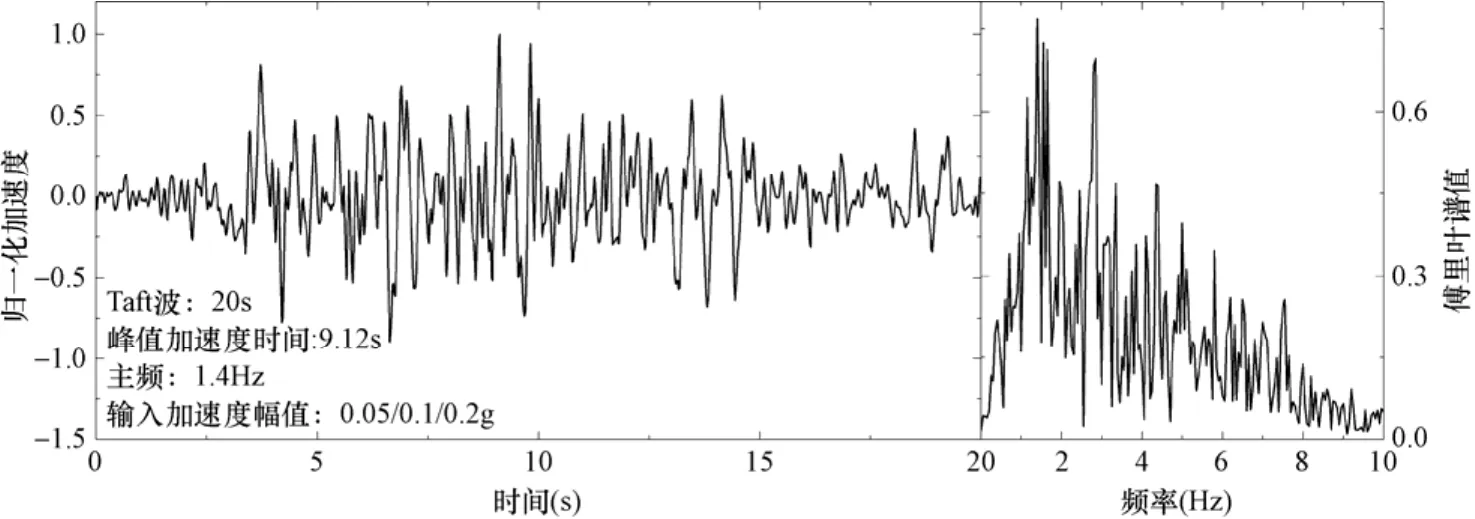
图5 基岩输入地震波时程曲线及FFT曲线（Taft波）Fig. 5 The time history and FFT property of the earthquake wave used as input in the rockbed （Taft wave）

2 计算结果

2.1 软土层对加速度幅值分布曲线的影响

软土层对加速度幅值分布曲线的影响如图6所示。其中，图6（a）、（b）给出了当软土层厚度分别为2m和4m时，软土层埋深变化对加速度幅值沿深度分布曲线的影响。可见：①加速度反应幅值分布曲线在软土层位置处发生突变，软土层埋深越大，加速度幅值分布曲线突变越明显；②当软弱夹层埋深较小时，软弱夹层的存在使得场地地面加速度幅值相比于同条件下不含软土层场地（以下简称“原场地”）的地面加速度幅值增大；③当软弱夹层埋深大于某一界限值后，将使得地面加速度幅值相比于原场地减小，且软土层埋深越大，衰减越多；④当埋深较小时，软土层厚度变化对接近地表的土层加速度幅值存在显著影响；当埋深较大时，软土层厚度对场地加速度幅值分布曲线的影响较小。如当埋深为4m时，厚度为2m的软土层使得地面加速度幅值相对于原场地增大；而厚度为4m的软土层使得地面加速度幅值相对于原场地减小。

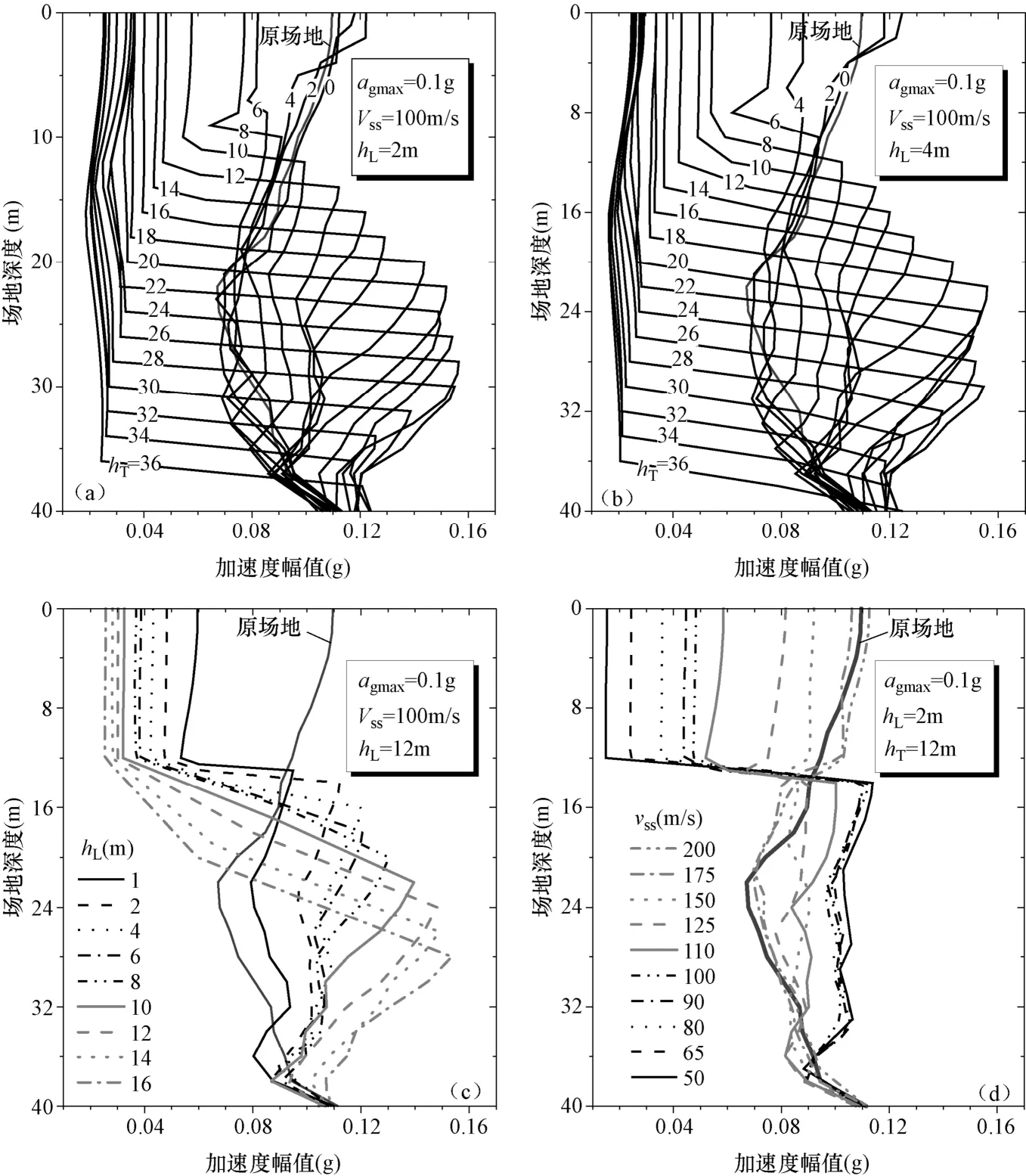
图6 深度一定时软弱夹层埋深变化对场地加速度幅值分布曲线的影响Fig. 6 Influence of the buried depth of a soft soil layer with defined thickness on profile of acceleration amplitude

图6（c）给出了在软土层的剪切波速和埋深一定时（νss=100m/s，hL=12m），场地内加速度幅值分布曲线随软土层厚度的变化情况。可见在剪切波速和埋深一定的情况下，随着软土层厚度的增大，场地加速度幅值分布曲线的突变也越大，由于这种突变使得地面峰值加速度随着软土层厚度的增大而减小。

图6（d）给出了当软土层厚度和埋深一定时（hL=2m，hT=12m），软土层剪切波速变化对场地反应的影响。可见：①随着软土层剪切波速的减小，地面加速度反应逐渐减小；②当软土层剪切波速相比于原场地土剪切波速降低不多时（如软土层剪切波速为νss=200m/s，vss=νss/νs=0.8），场地加速度反应幅值沿场地深度分布曲线在软土层处向增大方向发生突变、地面加速度幅值相对于原场地略微增大；③当软土层剪切波速相比于原场地土剪切波速降低较多时（如软土层剪切波速小于等于150m/s，vss≤0.6），场地加速度反应幅值沿场地深度分布曲线在软土层处向减小方向发生突变、地面加速度幅值相对于原场地减小，且软土层剪切波速越小，地面加速度幅值相对于原场地减小得越多。

2.2 软土层对地面峰值加速度的影响

图7给出了含软土层场地的地面峰值加速度与原场地的地面峰值加速度的比值（以下简称软土层的加速度效应系数）随软土层特性变化的规律。

由图7可见：①当软土层埋深较小时，加速度效应系数大于1，且在一定范围内加速度效应系数随着埋深的增大先增大后减小，当软土层埋深超过某临界值以后，加速度效应系数小于1，且随着软土层埋深的增加而减小；②软土层厚度越大，其对地面峰值加速度的影响越大，表现为厚度大的曲线两端均离图中灰色虚线（代表效应系数为1）越远；③软土层剪切波速越小，对地面加速度的衰减效应越明显；④软土层对地面加速度幅值的影响随着基岩输入加速度的增大而更显著。

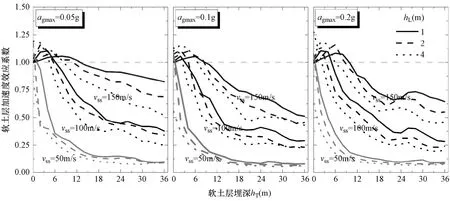
图7 软弱夹层埋深及厚度对软土层加速度效应系数的影响Fig. 7 Effect of thickness and depth of the inter soft soil layer on the ground acceleration amplification factor

图8进一步给出了在不同基岩输入地震波幅值下，软土层的加速度效应系数随软土层剪切波速变化的规律，图中软土层厚度4m，埋深从0m到36m变化。由图可见：①当软土层埋深较小时，软土层加速度效应系数随着软土层剪切波速的减小而先增大后减小，加速度效应系数会出现大于1的情况；②当软土层埋深大于某一界限深度时，软土层的加速度效应系数始终小于1，且随着软土层剪切波速的减小而减小；③当vs/vss在1—2之间时，较大基岩输入加速度幅值下的软土层加速度效应系数更小，说明基岩输入加速度增大会使得原本较硬的软土层变软，其软土夹层效应越明显。

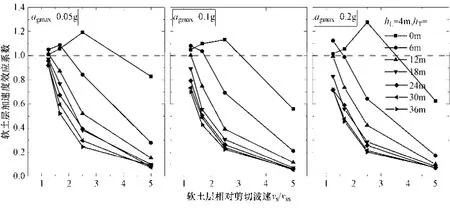
图8 软土夹层剪切波速对其加速度效应系数的影响Fig. 8 Effect of the shear wave velocity of soft layer on ground acceleration amplification factor

图9给出了软土层加速度效应系数随软土层埋深、厚度、相对剪切波速变化的三维曲面。图9（a）为hL-hT平面上的情况；图9（b）为vss-hT平面上的情况；图9（c）为vss-hL平面上的情况。图中浅色表示加速度效应系数大于1的区域，即软土层对地面加速度起放大效应；深色表示加速度效应系数小于1的区域，即软土层对地面加速度起衰减效应。各图底部平面的投影给出了软土层的加速度效应在相应平面上由放大到衰减的临界曲线。

由图9（a）可见，软土层加速度效应系数随软土层埋深和厚度的增大表现出先增大后减小的趋势。随着软土层剪切波速的不同，hL-hT平面上临界曲线的形状和位置也发生变化。软土层剪切波速越小，代表加速度效应系数大于1的浅灰色面积也就越小。

由图9（b）可见，软土层加速度效应系数随软土层埋深和相对剪切波速的增大表现出先增大后减小的趋势。随着软土层厚度的不同，vss-hT平面上各曲面的临界线形状和位置而变化，软土层厚度越大，临界线所围放大区域越小。

由图9（c）可见，软土层加速度效应系数随软土层厚度和相对剪切波速的增大表现出先增大后减小的趋势。vss-hL平面上的临界线形状和位置随着软土层埋深的不同而变化，随着软土层埋深的增加，临界线所围放大区域迅速减小。值得注意的是，当软土层埋深等于0时（即软土层位于场地表层），软土层对地面加速度幅值的影响以放大效应为主。

2.3 软土层对地面峰值加速度影响效应的临界曲面

由前面的计算结果可知，软土层对地面峰值加速度的效应系数受软土层厚度hL、埋深hT和剪切波速νss三个参数的共同影响，且可能存在一个空间临界面，当软土层的上述参数位于该临界面内外时，软土层对地面加速度分别起放大和衰减效应。要判断软土层的场地效应，应确定该临界面。

图10（a）给出了由图9中各曲面投影所得到的hL-hT平面上的临界曲线，图11（a）则给出了由图10中各曲面投影所得到的hT-vss平面上的临界曲线。可见，hL-hT平面上的临界曲线接近于直线，而hT-vss平面上的临界曲线则近似为双曲线。从应用简便出发，提出如下临界面方程：

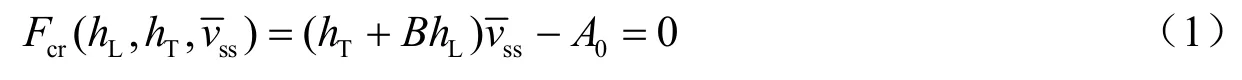
式中，hL表示软土层厚度；hT表示软土层埋深；vss=νss/νs表示软土层的相对剪切波速；νss为软土层的剪切波速；νs为原场地的剪切波速；A0、B为曲线参数。当Fcr＜0时，软土层对地面峰值加速度起放大效应；当Fcr＞0时，地面峰值加速度起衰减效应。

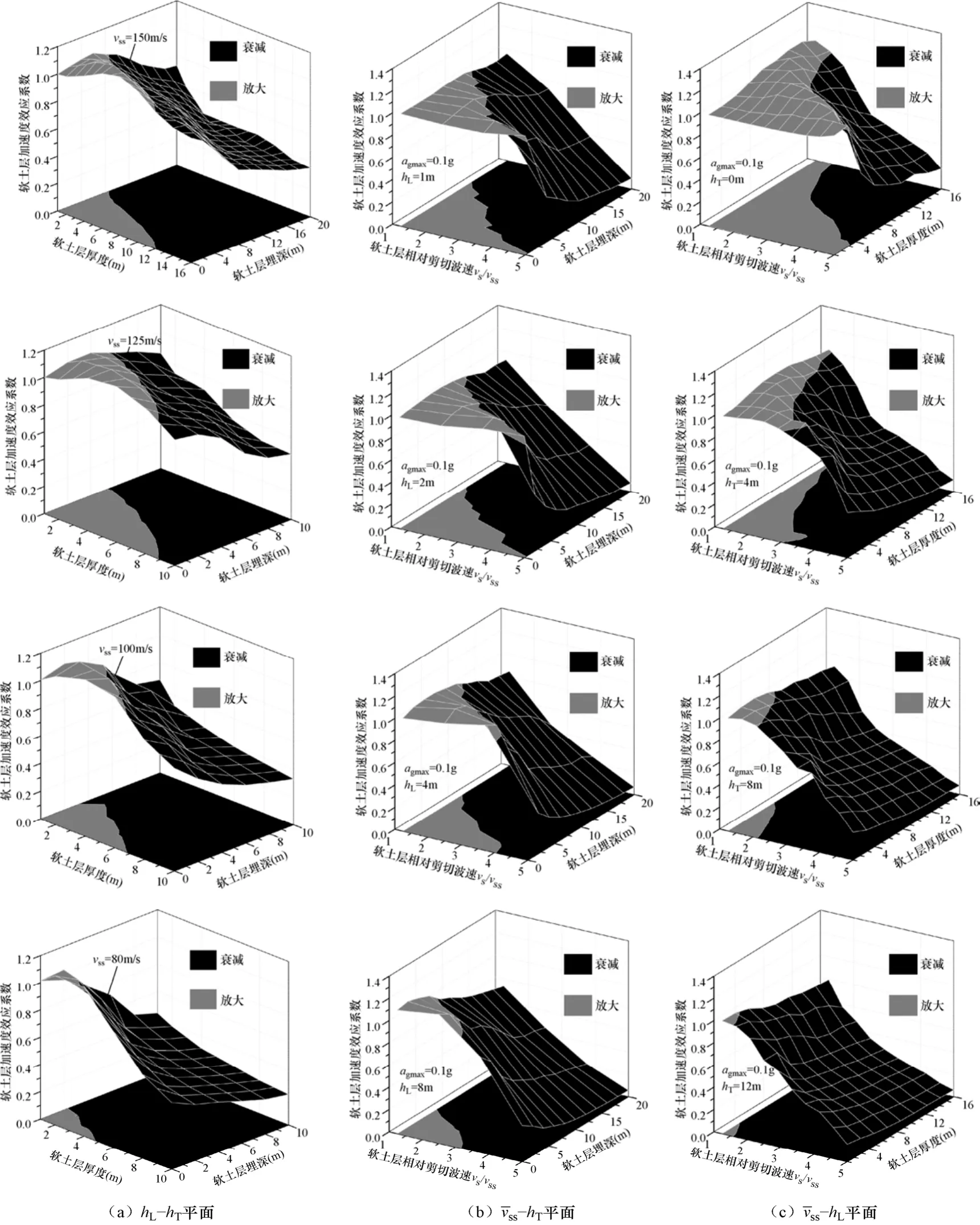
图9 软土层加速度效应系数随软土层厚度、埋深和相对剪切波速变化的规律Fig. 9 Effect of the thickness， buried depth and relative shear velocity of a soft layer on ground acceleration amplification factor

用式（1）对图10（a）、图11（a）中的临界曲线进行拟合，得到两个曲线参数的取值为：A0=13.5，B=0.5。拟合曲线分别绘制于图10（b）、图11（b）中，可见拟合的临界曲线可合理地代表计算临界线，且偏于安全（拟合曲线所给出的放大效应区域相对于计算曲线偏大）。

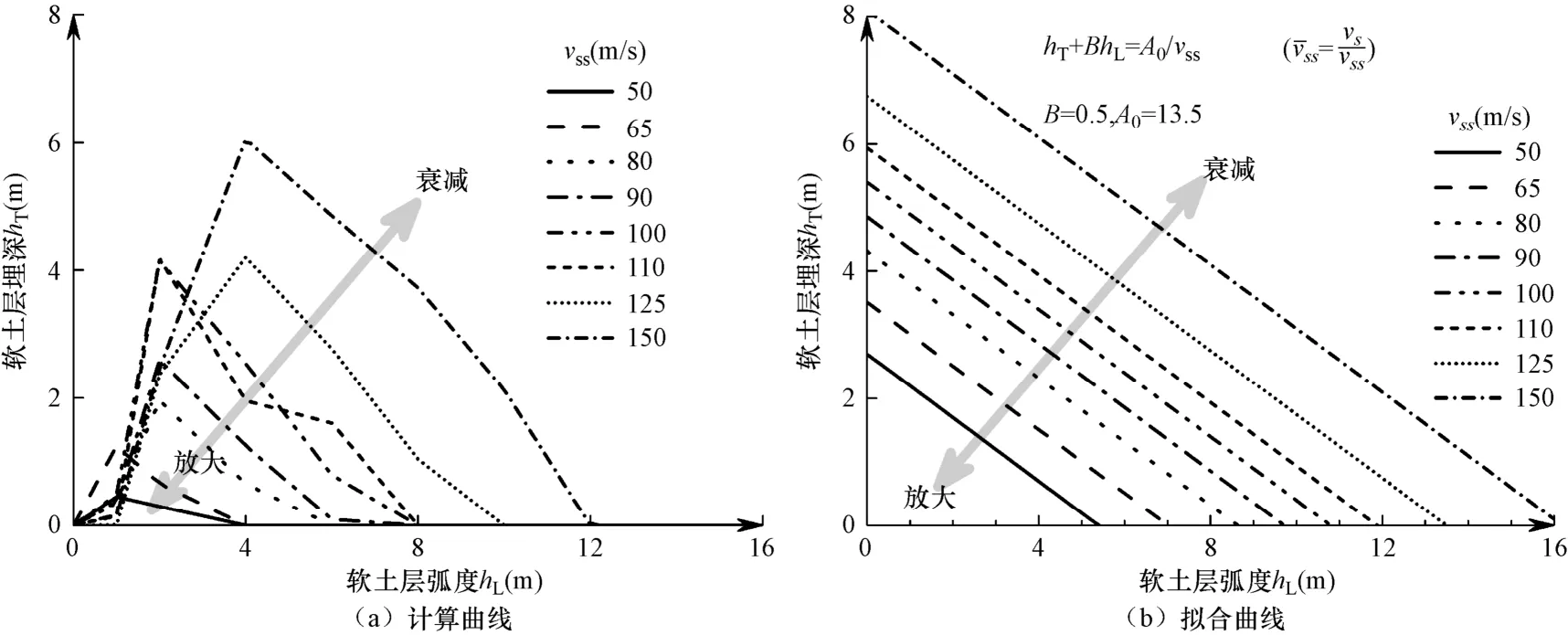
图10 软土层对地面加速度影响效应的临界曲线（hL-hT平面）Fig. 10 Critical curves representing the influence of soft soil layer on ground acceleration response （in the hL-hTplane）:

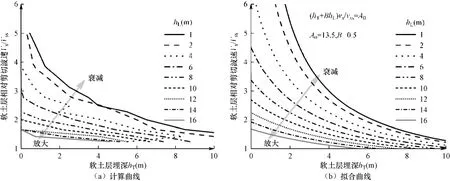
图11 软土层对地面加速度影响效应的临界曲线（hT-vss平面）Fig. 11 Critical curves representing the influence of soft soil layer on ground acceleration response （in the hT-vSSplane）

2.4 软土层对地面加速度影响效应的经验估计

已有对软土层场地效应的研究往往只限于定性的分析，且只强调了软土层对场地加速度反应的隔震效应而忽略了在某些情况下的放大效应。本文研究表明，随着软土层几何构造和剪切波速的不同，软土层可能对地面加速度峰值起衰减效应，但也可能起放大效应，如果忽略后一种情况，就有可能做出偏于不安全的预测。同时为了在场地分类、地震小区划等工程实践中更真实地考虑软土层的影响，有必要对软土层的加速度效应系数进行定量分析研究。

根据对本文计算结果的分析，软土层对地面峰值加速度的影响效应系数应该与临界面相关，在临界面以内，效应系数大于1；在临界面以外，效应系数可以取小于1的值，以考虑软土层隔震的有利影响。本文提出软土层对地面加速度的影响效应系数估计公式如下：

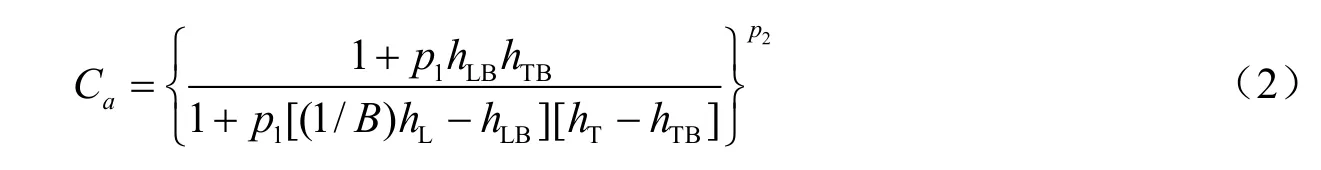
式中，Ca表示软土层对地面加速度的影响效应系数；hL、hT、vss分别表示软土层的厚度、埋深和相对剪切波速；hLB、hTB分别为由临界面方程确定的软土层临界厚度和临界埋深，由式（1）推得：

式中，A0、B为临界曲面参数，取值亦与式（1）相同；p1=0.01，p2=0.5为曲线参数。

图12给出了当软土层剪切波速νss为100m/s时，由式（2）所估计的软土层加速度效应系数随软土层几何构造特性的变化曲线与计算曲线的对比。图12（a）、（c）表示了不同软土层埋深下的加速度效应系数随软土层厚度变化的曲线；图12（b）、（d）表示了不同软土层厚度下的加速度效应系数随软土层埋深变化的曲线。可见式（2）较好地反映了软土层加速度效应系数随软土层厚度和埋深变化的规律，即当软土层厚度和埋深均很小时，效应系数大于1且随厚度和埋深的增大表现出先增大后减小；当软土层厚度和埋深超过临界值后，效应系数小于1且随着厚度和埋深的增大而降低。由图可见，在相同条件下的估计曲线比计算曲线偏高，说明应用式（2）估计软土层的场地效应是偏于安全的。

对图13第一、二排四幅图进一步给出了在不同软土层剪切波速下，由式（2）所估计的效应系数随软土层厚度和埋深变化的三维曲面与计算曲面的对比，可见在不同的软土层剪切波速下，估计曲面均较好地模拟了计算曲面的变化规律，且估计值比计算值高。

根据本文计算结果，软土层位于临界面之内时的地面加速度效应系数大于1但最大值亦未超过1.2，而在临界面外的效应系数最小值接近0.1，直接应用式（2）估计软土层的效应系数偏于保守。为更合理地预测软土层的加速度效应，对式（2）进一步修正如下：

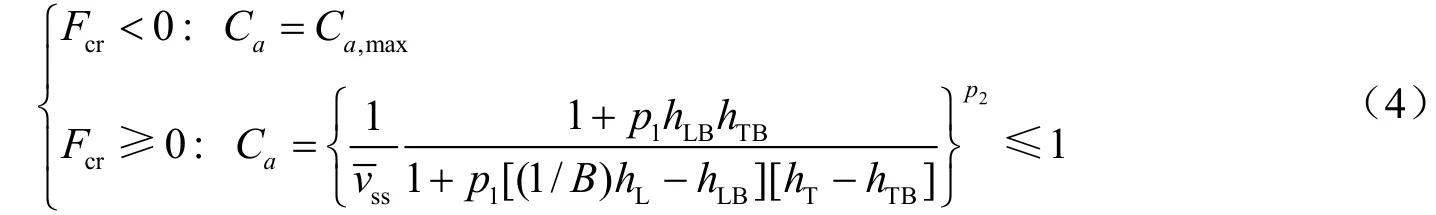
式中，Fcr表示临界曲面，其方程由式（2）代表；Ca，max表示软土层加速度效应系数最大值，根据本文计算结果，可取为1.2；其他各参数意义同式（2）。上式的物理意义为，当软土层的几何构造和剪切波速参数位于临界面以内时，软土层对地面加速度起放大效应，此时为保守起见对软土层的加速度效应系数取最大值，因此临界面内的效应系数为一平台面；当软土层的几何构造和剪切波速参数位于临界面以外时，软土层对地面加速度起衰减效应，对软土层加速度效应系数取一个不大于1的估计值。

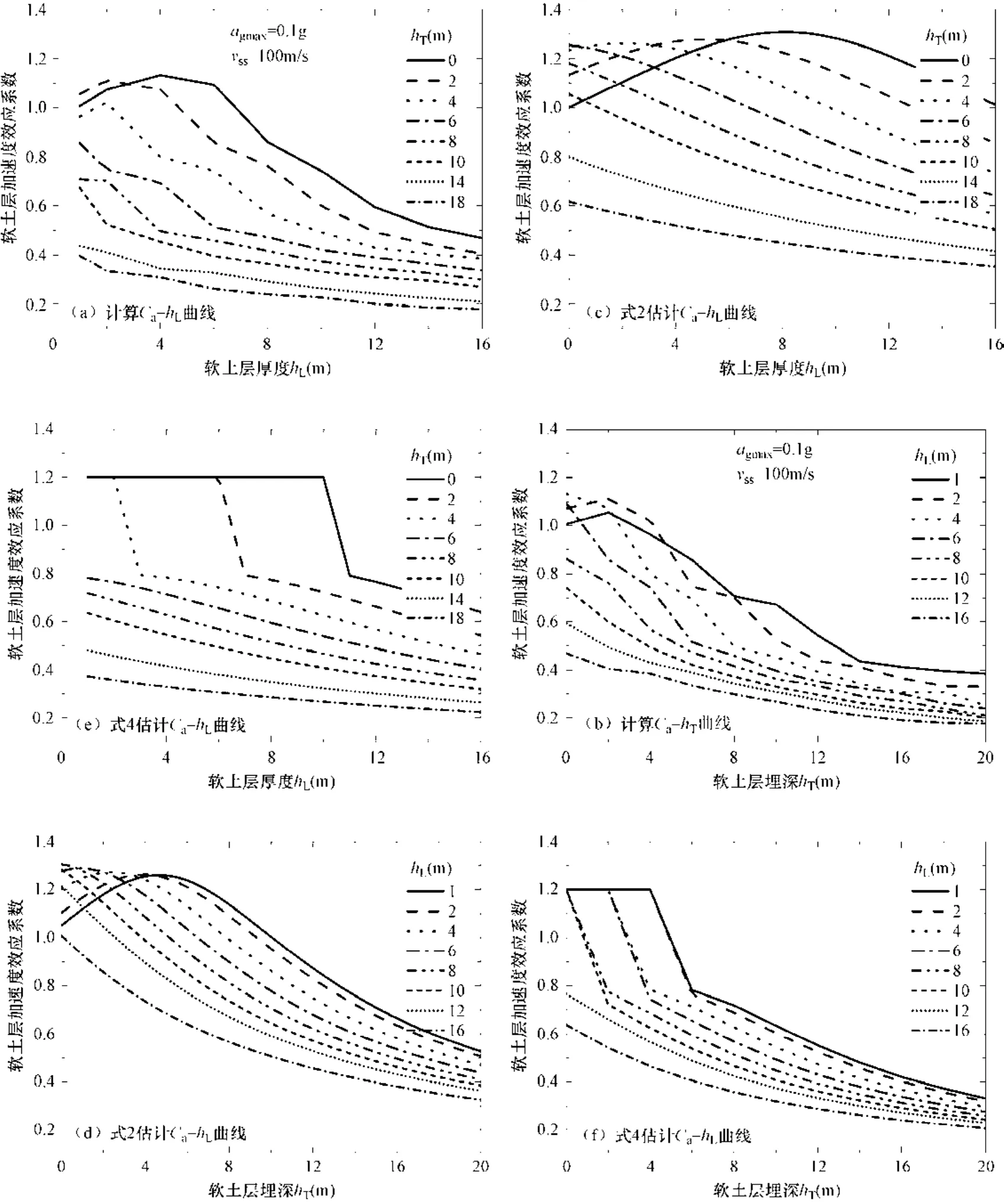
图12 软土层对地面加速度影响效应系数随软土层几何构造参数的变化关系曲线Fig. 12 Relationship between the influence factor of soft soil layer on PGA and geometric parameters of the soft layer

作为对比，式（4）所代表的加速度效应系数随软土层几何构造参数变化的曲线和三维曲面也同时分别绘制于图13。由图可见，相比于式（2），修正后的式（4）能更好地模拟计算值，由式（4）所得到的加速度效应系数曲面与计算曲面更为吻合。

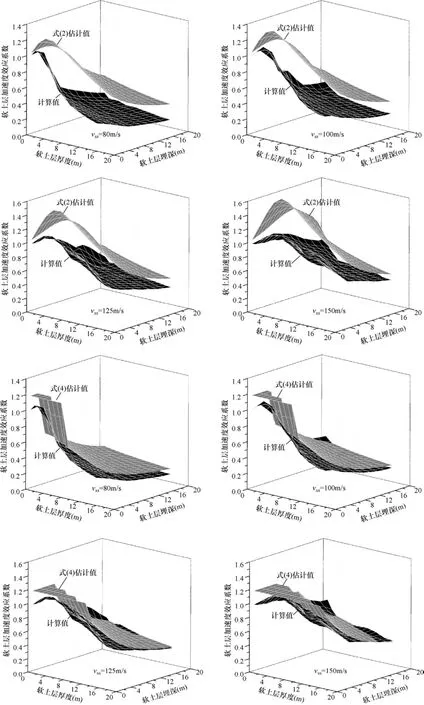
图13 软土层加速度效应系数估计值与计算值对比Fig. 13 Comparison of the influence factor of acceleration response between estimated and calculated

3 结论

本文应用一维真非线性场地反应分析方法，对某单层匀质场地内软土层的几何特性和剪切波速变化对地面加速度幅值的影响进行了数值分析，得到了如下结论：

（1）软土层的存在使得场地加速度幅值分布在软土层处发生突变，随着软土层几何特性和剪切波速的不同，这种突变可能使得地面峰值加速度增大或减小。

（2）软土层对地面峰值加速度的影响受几何特性和剪切波速的共同影响，存在一个由厚度hL、埋深hT和相对剪切波速ss三个参数构成的临界状态函数Fcr（hL，hT，ss），当Fcr＜0时，软土层对地面峰值加速度起放大效应，且加速度效应系数随着上述三个变量的增大表现出先增大后减小的变化规律；当Fcr＞0时，软土层对地面峰值加速度起衰减效应，加速度效应系数随着软土层的厚度、埋深和相对剪切波速的增大而减小。

（3）提出了可定量估计软土层加速度效应系数的经验公式，与计算结果的对比验证表明，经验公式能合理地反映不同几何特性和剪切波速下，软土层对地面峰值加速度的影响，可为相关应用提供参考。

需要指出的是，本文经验公式仅针对匀质场地，对于复杂土层结构中软弱夹层的场地效应的适用性还有待进一步深入研究。

薄景山，李秀领，刘红帅，2003a.土层结构对地表加速度峰值的影响.地震工程与工程震动，23（3）：35—40.

薄景山，李秀领，刘德东等，2003b.土层结构对反应谱平台值的影响.地震工程与工程震动，23（4）：29—33.

薄景山，李秀领，刘德东等，2003c.土层结构对反应谱特征周期的影响.地震工程与工程震动，23（5）：42—46.

薄景山，翟庆生，吴兆营等，2004.基于土层结构的场地分类方法.地震工程与工程震动，24（4）：46—49.

陈国兴，陈继华，2004.软弱土层的厚度及埋深对深厚软弱场地地震效应的影响.世界地震工程，20（3）：66—73.

黄润秋，余嘉顺，2003.软弱夹层的地震动强度效应研究.自然科学进展，13（11）：1177—1181.

黄玉龙，郭迅，袁一凡等，2000.软泥夹层对香港软土场地地震反应的影响.自然灾害学报，9（1）：109—116.

金丹丹，陈国兴，董菲蕃，2012.软夹层土对福州盆地地表地震动特性的影响.武汉理工大学学报，34（12）：83—88.

卢华喜，梁平英，仇早生，2010.软弱土层对中欧场地划分影响的比较.工业建筑，40（2）：82—85.

栾茂田，林皋，1992.场地地震反应一维非线性计算模型.工程力学，9（1）：94—103.

钱胜国，1994.软土夹层地基场地土层地震反应特性的研究.工程抗震，（1）：32—36.

尚守平，刘方成，王海东，2007.基于阻尼的地震循环荷载作用下粘土非线性模型.土木工程学报，40（3）：74—81.

史丙新，吕悦军，2010.软弱场地的地震动效应研究.见：中国地震局地壳应力研究所，地壳构造与地壳应力文集（22）.北京：地震出版社，24—33.

谢君斐，石兆吉，1978.天津市震害异常的初步探讨.哈尔滨：中国科学院工程力学研究所.

张建毅，薄景山，林玮等，2013.北川县城土层特性对地震动的影响.自然灾害学报，22（1）：130—139.

Bardet J.P. and Tobita T.， 2001. NERA- A computer program for nonlinear earthquake site response analyses of layered soil deposits （Manual）. Department of Civil Engineering， University of South California.

Idriss I.M.， Sun J.I.， 1992. Shake91-A computer program for conducting equivalent linear seismic response analysis of horizontally layered soil deposits （User’s Manual）. Department of Civil and Environmental Engineering， University of California， Davis， California.

Seed H.B.， Idriss I.M.， 1970. Soil moduli and damping factors dynamic analysis. Report NO. EERC 70—10，Earthquake Engineering Research Center， University of California， Berkley.

Seed H.B.， Wong R.T.， Idriss I.M.， and Tokimatsu K. ， 1986. Moduli and Damping Factors for Dynamic Analyses of Cohesionless Soils. Journal of Geotechnical Engineering， 112（11）: 1016—1032.

Influence of the Geometric Properties and Shear Wave Velocity of a Soft Soil Layer on the PGA Response of Site

Liu Fangcheng， Wu Jingfang， Chen Bin and Zhao Chengqi

（College of Civil Engineering， Hunan University of Technology， Zhuzhou 412008， China）

The earthquake response of soil deposits containing a soft layer has been of great interest in geotechnical earthquake engineering practice. This paper introduces a study on the influence of a soft layer on the ground motions of a homogeneous deposit， with the variation of geometric properties and shear wave velocity of the soft layer. Numerical studies are conducted by method of real nonlinear one dimensional site response analysis. Results indicate that the existence of a soft soil layer in the deposit will cause sudden change of the acceleration response in the profile， and the PGA may be increased or decreased based on the geometric properties and shear wave velocity of the soft soil. There exists a critical range as which being exceeded the PGA will be decreased monotonically with the increase of the soft soil’s thickness， buried depth and relative shear wave velocity. On the contrary， as the critical range is not exceeded， the PGA will be enlarged in a trend of decreasing after increasing with the increase of the soft soil’s thickness， buried depth and relative shear wave velocity. Formula describing the critical range and empirical methods estimating effects of a soft soil layer on PGA are proposed based on parametric analysis of a homogeneous site. Reasonability of proposed method is validated by numerical calculation results. Foundations of this study may provide reference for further research and application.

Soft soil layer； Site effects； Soil dynamic properties； Site response analysis； Peak ground acceleration

国家自然科学基金项目（51108177）；湖南工业大学自科基金项目（2012HZX20、2013HZX09）

2015-03-05

刘方成，男，生于1978年。博士，副教授。主要从事土动力学、场地效应及土-结构动力相互作用研究。E-mail: 455211101@qq.com。