铅芯橡胶支座在旧桥抗震加固中的应用

米曦亮，胡 鹏

(北京市市政工程设计研究总院有限公司，北京市100082)

铅芯橡胶支座在旧桥抗震加固中的应用

米曦亮，胡 鹏

(北京市市政工程设计研究总院有限公司，北京市100082)

针对某旧桥不满足抗震性能要求的问题，提出采用铅芯橡胶支座进行减震。以双线性模型模拟支座，并选取合适的地震波时程对桥梁下部结构进行时程分析。结果表明，E2地震下结构内力大幅削减，变形满足要求，实现了抗震加固的目标。

旧桥;铅芯橡胶支座;抗震加固;时程分析

0 引言

根据中国公路学会报告，到2013年底，全国共有公路桥梁73.53万座，市政桥梁约5万座，我国已经跻身于世界桥梁大国［1］。但另一方面，大量兴建于上世纪八九十年代的桥梁经过二三十年的服役，已经出现了种种病害，桥梁局部构件损坏、整体垮塌等现象屡有发生。而桥梁抗震设计理论也不断发展，抗震设计方法已经从原来的拟静力法发展到现在的延性设计理论，从仅关注结构在多遇地震下的承载能力发展到确保结构在E2地震下不出现整体垮塌，对桥梁下部结构能力保护设计提出了明确的要求，部分老旧桥梁已经不能满足新的抗震要求。综合前面的原因，对老旧桥梁的改造已经迫在眉睫。桥梁上部结构的加固方式较多，粘钢板、增设钢托梁、张拉体外预应力等都是成熟可靠的方法，而下部结构的加固方式则相对较少，本文提出采用更换铅芯橡胶支座来进行减震设计，减小下部结构内力，使其在E2地震作用下满足抗震性能要求。

1 某现况桥梁简介

北京地区某现况桥梁兴建于1985年，长1 km，宽15 m，上部结构为50跨20 m简支T梁，下部结构为排架式墩柱接盖梁形式，基础为1.5 m钻孔灌注桩，桩顶设系梁连接。该桥梁位于交通量繁重的郊区二级道路上，货运大车较多，经过二十多年的使用桥梁已经出现较多病害(见图1)。

2010年，在对桥梁所处道路进行改扩建之前，对桥梁结构进行了详细的检测评估和计算分析，桥梁的抗震验算结果如下:

图1 现况桥梁实景

(1)在E1地震下，下部结构满足承载力要求;

(2)在E2地震下，墩柱斜截面抗剪、盖梁正截面抗弯承载能力不满足能力保护构件要求;

(3)墩柱和桩基的箍筋配置较少，潜在塑性铰区域未加密，不满足抗震构造要求，延性不足。

针对上述问题，本文拟采用铅芯橡胶支座对桥梁进行减震设计，目标是减小E2地震下部结构的内力，使其仍处于弹性范围内。这样，就能避免因主筋和箍筋不足造成的不满足塑性铰区域构造要求问题和不满足能力保护要求问题。

2 铅芯橡胶支座的力学性能

铅芯橡胶支座是在普通板式橡胶支座的中部或中心周围部位竖直压入一个或几个高纯度铅芯制成的，通过铅芯的剪切变形来吸收耗散振动能量。铅芯橡胶支座具有构造简单、加工制造容易、安装方便、设计阻尼有较大的灵活性(调节铅芯的几何尺寸)、耐疲劳性能好、在常态下刚度较大等优点，在工程实际中就得到了广泛应用。在我国、日本、美国和新西兰等国已建造了一千余座此类隔震结构，其中数座在1994年美国北岭地震和1995年日本阪神地震中经受了强烈地震动的考验，显现了良好的隔震效能［2］。

铅芯橡胶支座的本构关系是非线性的，最常用分析模型是双线性分析模型，模型图如2所示。

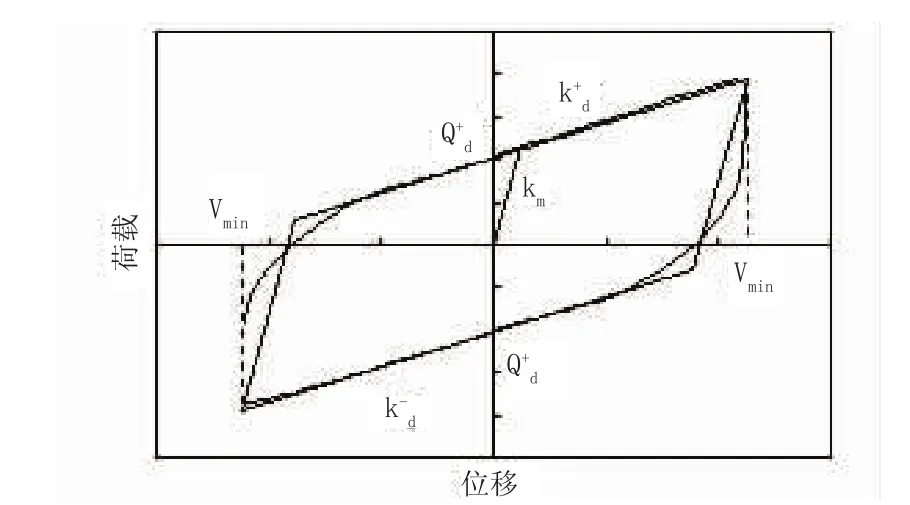
图2 铅芯橡胶支座的双线性分析模型图

在双线性模型中，主要力学参数包括弹性刚度Ku、屈服后刚度Kd、特征强度Qd等。对于这些力学参数与支座的结构参数，在一些国外规范及国内外文献中均有研究。日本桥梁免振设计条例提出了修正的双线性模型，其中弹性刚度Ku和屈服后刚度Kd随支座变化耳变化，但特征强度Qd保持为常数，这与试验结果不符，实际中采用较少;新西兰规范MWD CD818/A(1981)中，弹性刚度Ku和屈服后刚度Kd的比例关系为6.5，特征强度Qd为7.06D2(D为铅芯直径，mm)［3］。近些年来，国内较多研究者通过试验，亦提出了自己的本构关系模型。本文主要参考铁道科学研究院吴彬、庄军生等提出的双线性模型力学参数计算公式［4］，按OVMY2Q300及OVMY4Q300支座结构参数计算得到支座的力学模型。

3 计算模型

采用Midas/Civil 2006软件建立空间杆系模型，模拟支座的非线性本构关系，输入地震波进行时程分析。分析方法采用直接积分法，通过非线性迭代计算求得结构在各时间步的响应，结构阻尼采用振型阻尼0.05。

3.1 结构模型

各结构构件采用空间梁单元模拟，上部结构恒载以集中力均匀施加在各支座处;桩侧土约束根据“m”法用土弹簧模拟其水平约束刚度。图3为下部结构计算模型图。

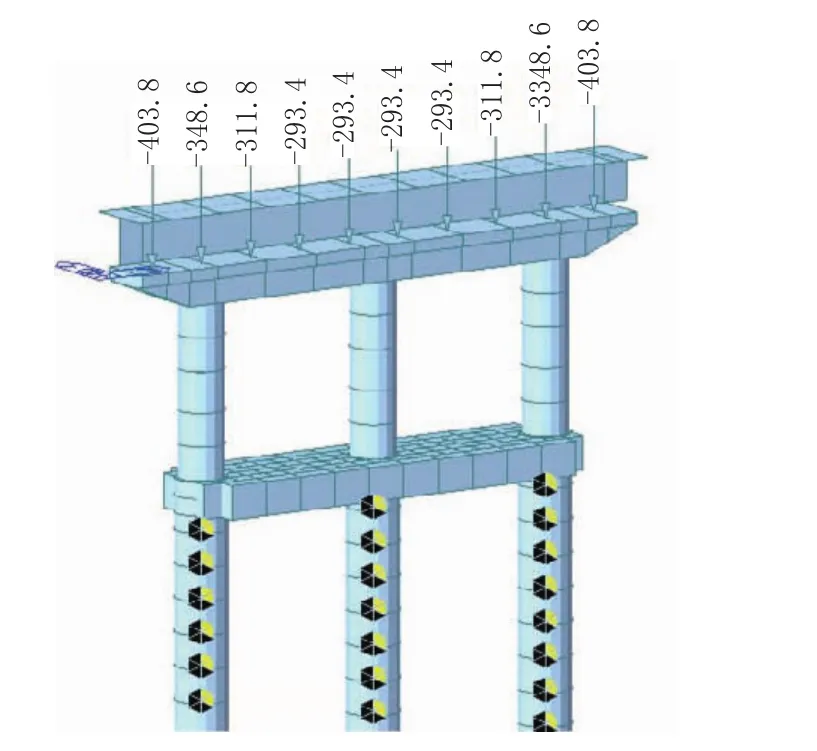
图3 下部结构计算模型图

3.2 支座力学模型

由静力计算得到，现况T梁单个支座所承受的最大反力约为285 kN，考虑到此次加固换梁的可能性，采用OVMY2Q300或OVMY4Q300支座，支座承载力440 kN，支座结构参数如表1所列。

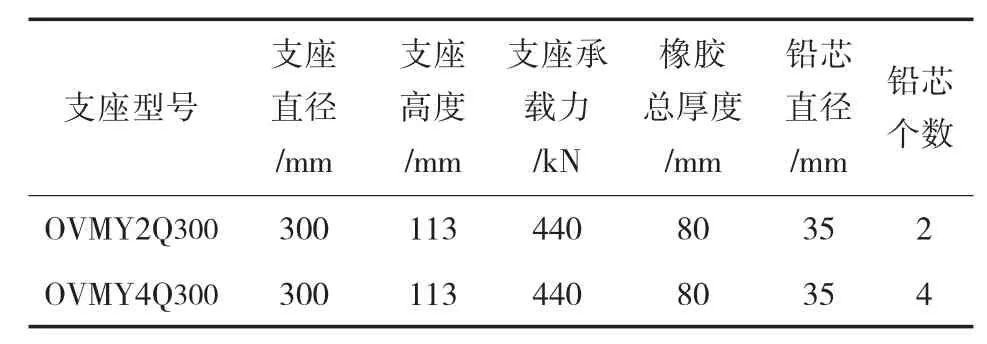
表1 OVM铅芯橡胶支座结构参数表

支座力学参数计算公式如下:

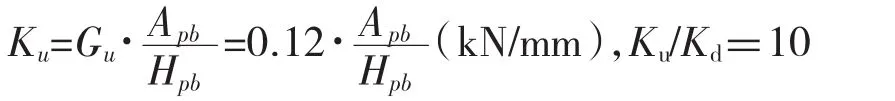
式中:Gu为支座的剪切模量，与剪切应变关系较大，在应变大于50%情基本稳定;Apb为铅芯的横截面面积，单位mm2;Hpb为铅芯的有效变形高度，等于橡胶总厚度，mm。

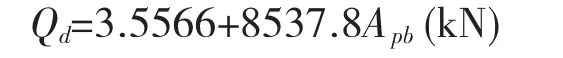
式中:Apb为铅芯的横截面面积，m2。

表2为OVM铅芯橡胶与压力学参数表，图4为OVMY4Q300支座本构关系模型图。

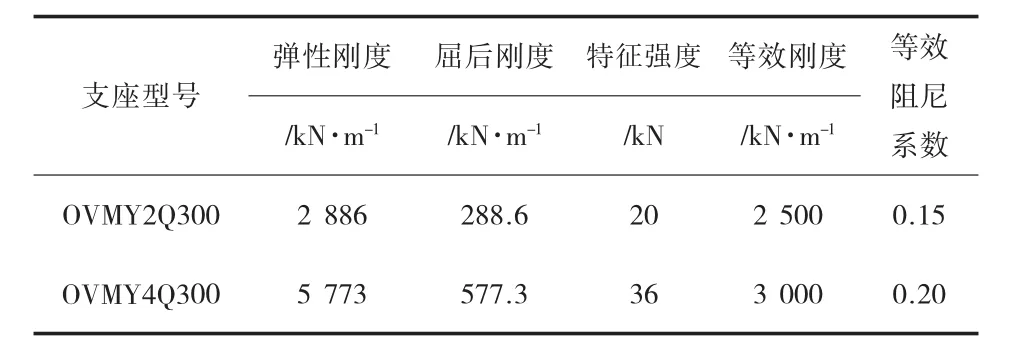
表2 OVM铅芯橡胶支座力学参数表

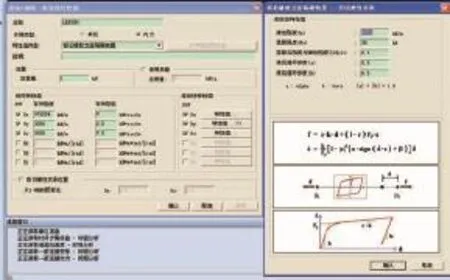
图4 OVMY4Q300支座本构关系模型图

3.3 地震波检验

由于桥位处未做地震安全性评价，故只能采用与抗震细则中加速度反应谱兼容的实际地震波或人工合成时程计算。根据《建筑抗震设计规范》(GB 50011-2001)第5.1.2条规定，地震加速度时程应满足地震动三要素的要求，即频谱特性、有效加速度峰值和持续时间要符合规定。

根据1978年美国ATC-3规范，在阻尼比为5%的加速度反应谱中取周期为0.1～0.5 s之间的值平均为Sa，在阻尼比为5%的速度反应谱中取周期为0.5～2 s之间的值平均为Sv(或取1 s附近的平均速度反应谱)。地震波的三要素计算如下:

有效峰值加速度EPA=Sa/2.5

有效峰值速度 EPV=Sv/2.5

特征周期 Tg=2π·EPV/EPA

有效峰值加速度EPA应满足《建筑抗震设计规范》(GB 50011-2001)表5.1.2-2的要求:对于设防烈度8度，动峰值0.2 g地区的罕遇地震，时程曲线最大值应为0.4 g;特征周期Tg应与桥位场地特征周期相同或接近;持续时间取地震动幅值大于0.05 g的时间总和。在计算中采用1940 EI Centro Site，180Deg时程及某人工合成时程分别进行检验，选择合适的时程用于减振计算(见图5～图10)。

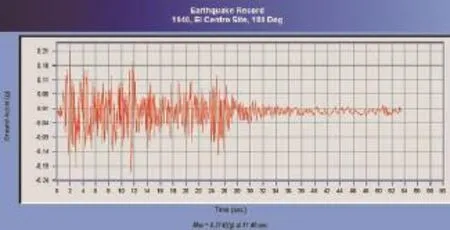
图5 1940年EI Centro Site,180De9时程曲线图

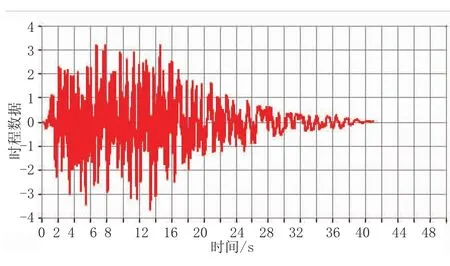
图6 某人工合成时程曲线图

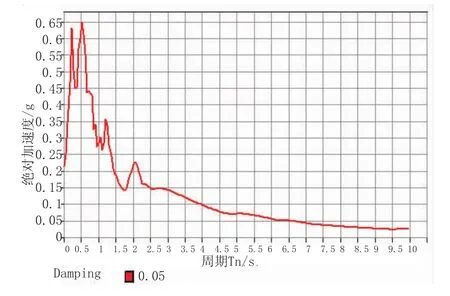
图7 EI Centro Site时程对应的绝对加速度反应谱曲线图

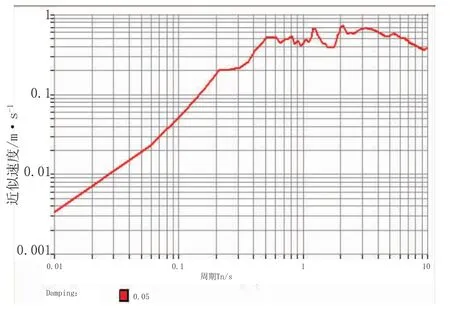
图8 EI Centro Site时程对应的近似速度反应谱曲线图

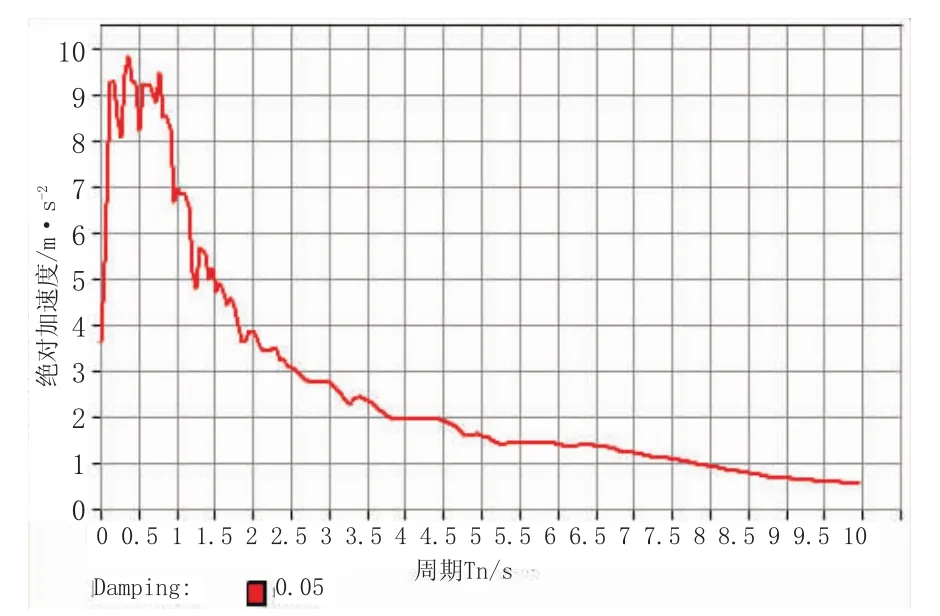
图9 某人工合成时程对应的绝对加速度反应谱曲线图

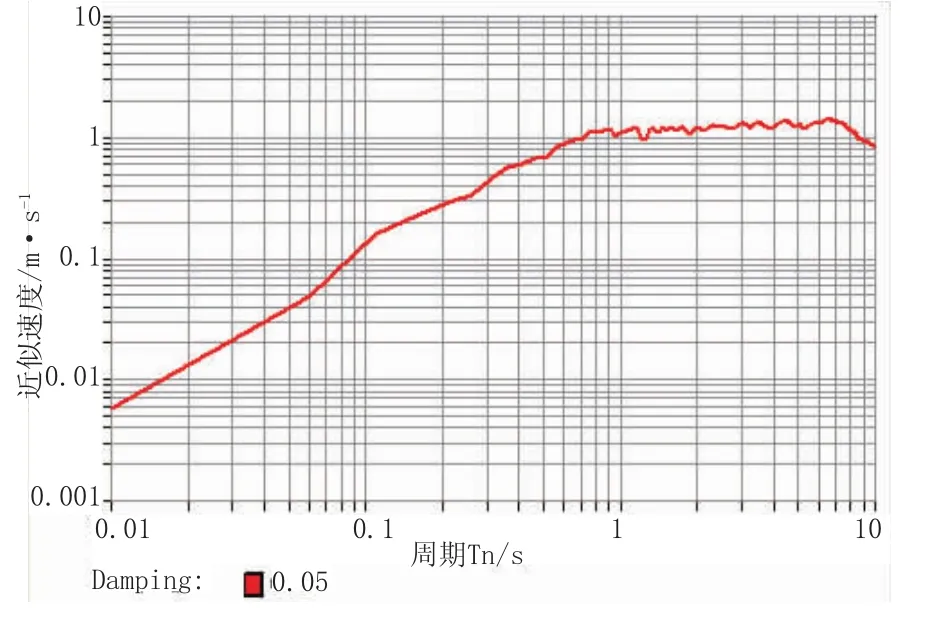
图10 某人工合成时程对应的近似速度反应谱曲线图

从图5～图10可以得到，对于1940 EI Centro Site，180Deg时程，Sa=0.5 g，Sv=0.5 m/s，由此可得，EPA=0.2 g，EPV=0.2 m/s，Tg=2×3.1416×0.2/2=0.63(s);

对于人工合成时程，Sa=9.1 m/s2，Sv=1.05 m/s，由此可得，EPA=3.64 m/s2，EPV=0.42 m/s，Tg=2× 3.1416×0.42/3.64=0.72(s)。

两条时程的特征周期均与场地特征周期0.35 s有一定差距，有效加速度峰值可以通过放大系数调整;从持续时间看，35 s以后两条时程的幅值均小于0.05 g。从加速度反应谱看，人工合成时程与规范反应谱形状更为接近，故取其计算。通过放大系数1.1调整幅值至0.4 g。

4 计算结果

分别计算了不采用铅芯支座时结构在E2规范反应谱、人工时程下的响应，以及采用铅芯支座(OVMY2Q300、OVMY4Q300)减振时结构在人工时程下的响应(见图11、图12及表3)。

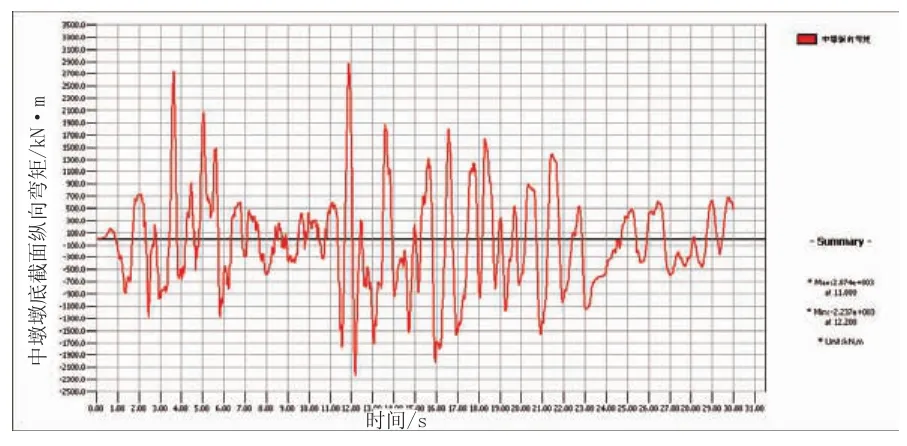
图11 不采用铅芯支座时在人工合成时程下中墩墩底截面纵向弯矩时程曲线图

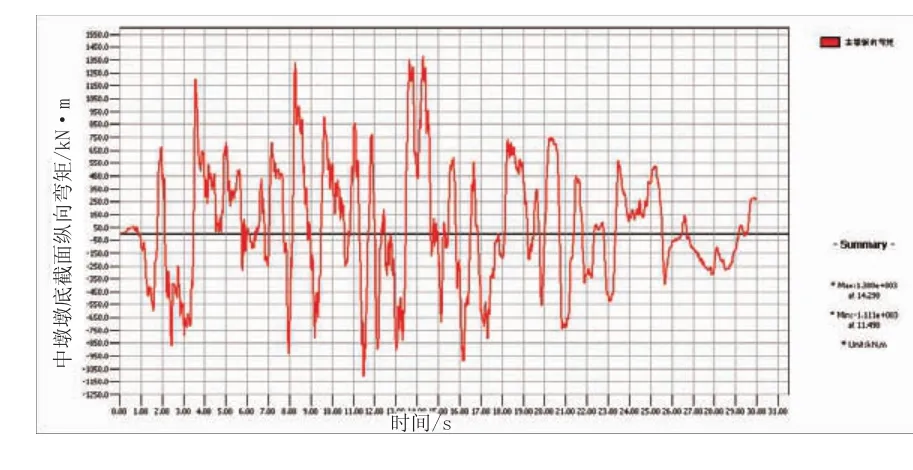
图12 采用OVMY4Q300支座时在人工合成时程下中墩墩底截面纵向弯矩时程曲线图

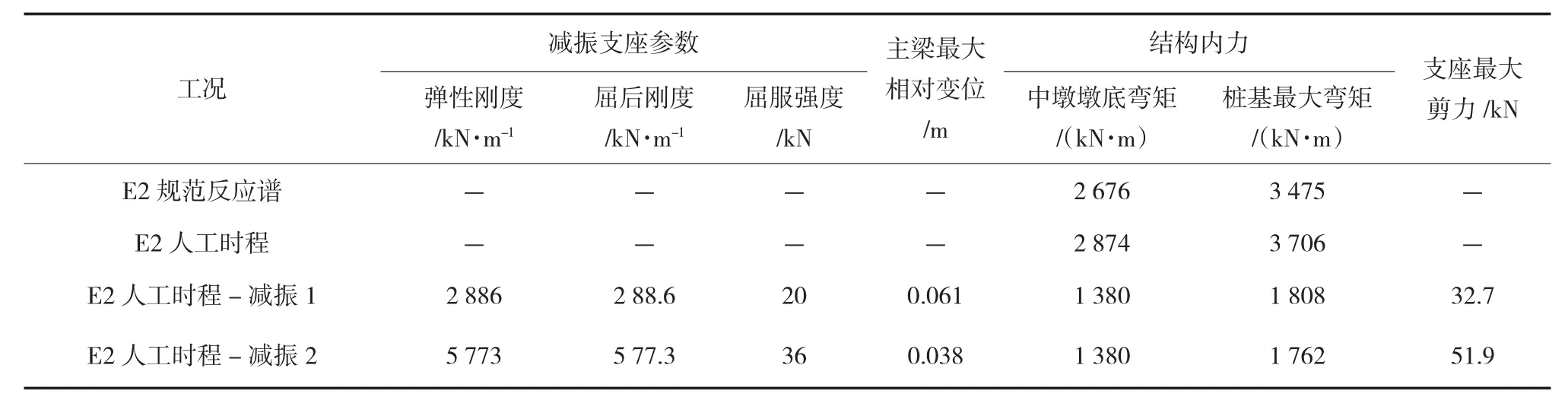
表3 各项工况计算结果汇总表

结论:

(1)人工时程得到的最大内力略大于反应谱结果，时程取用合适。

(2)采用OVMY4Q300支座时，墩柱内力及桩基最大弯矩减少约52%，减振效果明显，经验算，墩柱及桩基承载能力满足要求。主梁相对于盖梁的纵向位移最大为3.8 cm，变位较小，现有变形缝宽度满足位移要求。

5 结语

本文采用国内学者提出的参数计算公式以双线性模型模拟铅芯橡胶支座，对该支座在某旧桥抗震加固中的减震性能进行了详细分析。通过频谱特性、有效加速度峰值和持续时间等三要素的检验，选定了适合桥梁场地特性的地震波。地震波时程分析结果表明，结构在E2地震下的内力得到了大幅削减，仍处于弹性工作范围，满足了《公路桥梁抗震细则》的要求，实现了抗震加固的目标。

［1］ 赵君黎. 公路桥梁学科发展 ［A］. 2014年全国桥梁学术会议论文集［C］.珠海:2014.

［2］ 江宜城，聂肃非，叶志雄，李黎. 多铅芯橡胶隔震支座非线性力学性能试验研究及其显式有限元分析［J］. 工程力学，2008，25(7).

［3］ 张辉，戴公连. 武广高速铁路陈村水道特大桥地震响应及支座优化研究［J］. 城市道桥与防洪，2008，(7).

［4］ 吴彬，庄军生，臧晓秋. 铅芯橡胶支座的非线性动态分析力学参数试验研究［J］工程力学，2004，21(5).

U455.7+2

B

1009-7716(2015)04-0074-04

2015-01-23

米曦亮(1982-)，男，湖南岳阳人，工程师，从事桥梁工程设计工作。